Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

92 THE SIMPLEX METHOD

The above discussion implies that we can reduce the size of our tableau form by

keeping only the (−z) column, the columns corresponding to x

, and the updated

right-hand side. With these we can generate the reduced cost ¯c and the incoming

column

•s

. The reduced size tableau is shown below in Table 3-4. Thus, we never

(−z) x

RHS x

1 −π

−π

b ¯c

−1

•s

←− Pivot on

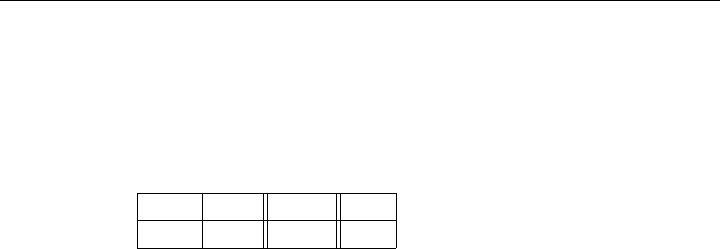
Table 3-4: Revised Simplex Tableau Iteration t

explicitly compute

A. This is what gives considerable savings in storage space. To

update the revised simplex tableau, Table 3-4 is pivoted on in the last column on

element ¯a

. Thus the

b for the next iteration is computed by the pivot step.

 Exercise 3.26 In Phase I we replace the objective (3.62a) by the infeasibility form

(−w)+e

=0.

Show that canonical form at the start of Phase I is

(−w) − e

Ax +0x

Ax + Ix

= b.

Write down the steps of the Revised Simplex Algorithm for Phase I. Next write down the

steps of the Revised Simplex Method.

3.5.2 REVISED SIMPLEX METHOD ILLUSTRATED

Example 3.3 (Revised Simplex Method) We shall illustrate the Revised Simplex

Method on the same Example 3.1 used to illustrate the Simplex Method in tableau form.

Namely, ﬁnd min z, x ≥ 0 such that

+1x

+2x

+ x

+4x

= z

+2x

+13x

+3x

+ x

=17

+ x

+5x

+ x

=7.

(3.64)

For ease of exposition we will display the entire tableau form but only show the quantities

that are determined explicitly or obtained by pivoting.

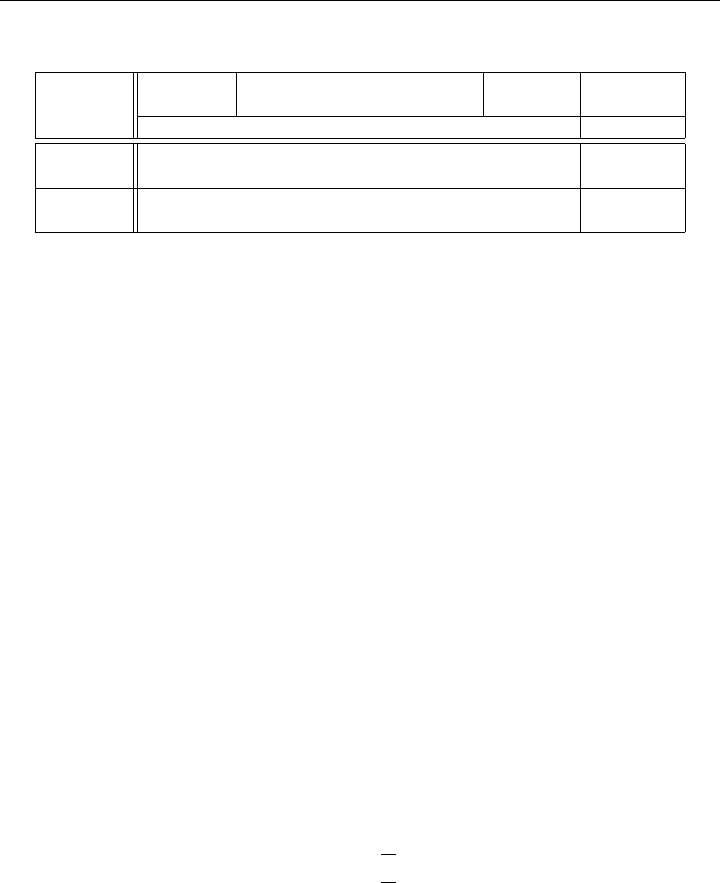
The detached coeﬃcient form for (3.64) is shown in Table 3-5. The coeﬃcients that

appear in the top row are d

= −e

•j

, where e =(1, 1,...,1)

. The Phase I reduced

costs

that will be computed on iterations 0, 1, and 2 of Phase I of the Revised Simplex

Method are stored in the −w line of each iteration in Table 3-6, as will be the reduced costs

¯c

for iterations 2 and 3 of Phase II in Table 3-7. Actually, in practice, in the Revised

Simplex Method, the

and ¯c

are computed but not stored; only the minimum value

or ¯c

is stored at the beginning of iteration t. Table 3-6 shows the recorded data at

the beginning of iteration t of the Revised Simplex Method. The column labeled “Basic

3.5 REVISED SIMPLEX METHOD 93

Detached Coeﬃcients of Original System

Basic Original Variables Artiﬁcial Constants

Variables Variables

−w −zx

−w 1 −5 −3 −18 −4 −2 −24

−z 121 214 0

4213311 17

11 511 1 7

Table 3-5: Detached Coeﬃcients

Variables” shows the names of the variables in the order (j

,...,j

) in the basis. The

relevant columns of the canonical form correspond to the artiﬁcial variables and contain

the negative of the simplex multipliers and the basis inverse. The simplex multipliers π

are the negative coeﬃcients of the artiﬁcials in the −w row in Phase I; in Phase II these

are in the −z row. The column after the last artiﬁcial variable is the modiﬁed right hand

side. These are obtained by pivoting.

To compute

and ¯c

directly from the original system Table 3-5, we will need the

simplex multipliers associated with iteration t. The numbers shown in italic (or boldface)

are generated directly from the original system. Recall that

= d

− π

•j

and ¯c

− π

•j

can be computed from the original data. If the solution is not optimal, we

determine the incoming column index s. The inverse of the basis is used to compute

•s

directly from the original data by the formula

•s

= B

−1

•s

. The pivoting transforms

column s to a unit column vector, which is not recorded.

On iteration 0, the Phase I basis inverse is the identity matrix (see Table 3-6), and hence

the entries shown in the table are the same as the corresponding entries from the original

data. Since the reduced cost

= −18 is the smallest, we bring in the corresponding x

into the basis on the next iteration. We are now in a position to determine which variable

leaves the basis; we compute

•3

= B

−1

•3

. Since B

−1

= I for this iteration,

•3

= A

•3

can be read oﬀ directly from the original data and entered in the corresponding column

of Table 3-6 for iteration 0. The updated column

•3

and

b allow us to locate the pivot

position, which is

. Pivoting on

drives x

out of the basis, replacing it by x

, and

generates the artiﬁcial columns and updated

b of the next iteration, t =1.

On iteration 1, the basis inverse is

−1



−



in the columns corresponding to x

and x

in Table 3-6. The simplex multipliers are

= −18/13 and π

= 0 which are the negative of the entries in the ﬁrst row in columns

corresponding to x

and x

. Thus the

can be computed by using (3.59) as d

− π

•j

for iteration 1 and so forth.

3.5.3 REVISED SIMPLEX METHOD ALGORITHM

The algorithm is described using B

−1

; in practice the inverse is not computed, but

instead the system of equations involving B is solved directly by an LU factorization

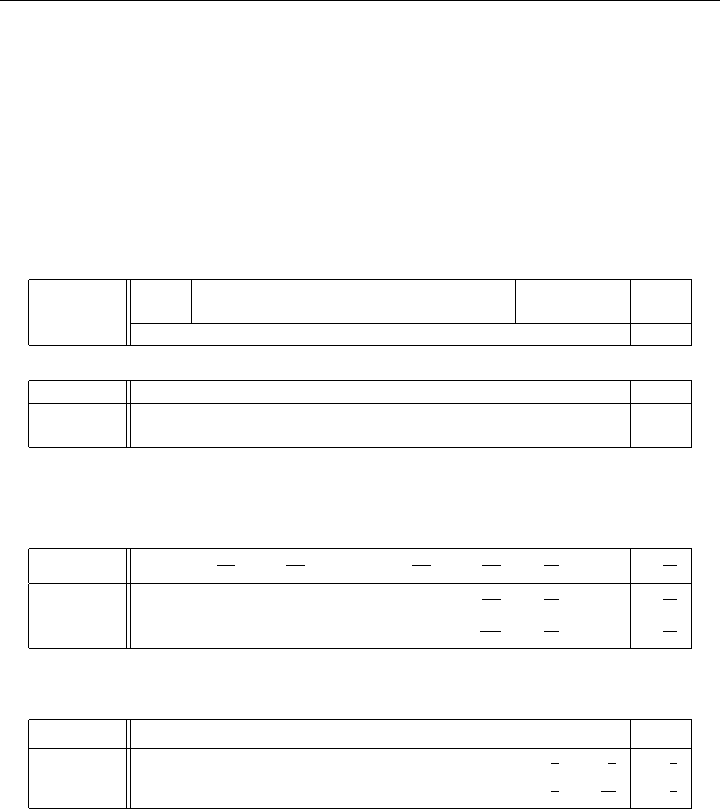
94 THE SIMPLEX METHOD

Iteration 0 (Phase I)

Basic OBJ Original Variables Artiﬁcial RHS

Variables Variables

−wx

•3

= B

−1

•3

−π

−w 1 − 5 − 3 − 18 − 4 − 2 00−24

13 1 17

5 1 7

−1

Iteration 1 (Phase I)

= d

− π

•j

−1

•5

−π

−w 1

−

−1

Iteration 2 (Phase I Optimal)

= d

− π

•j

≥ 0

−w 1 0000011 0

−

−1

Table 3-6: Revised Simplex Method: Tableau Form Example

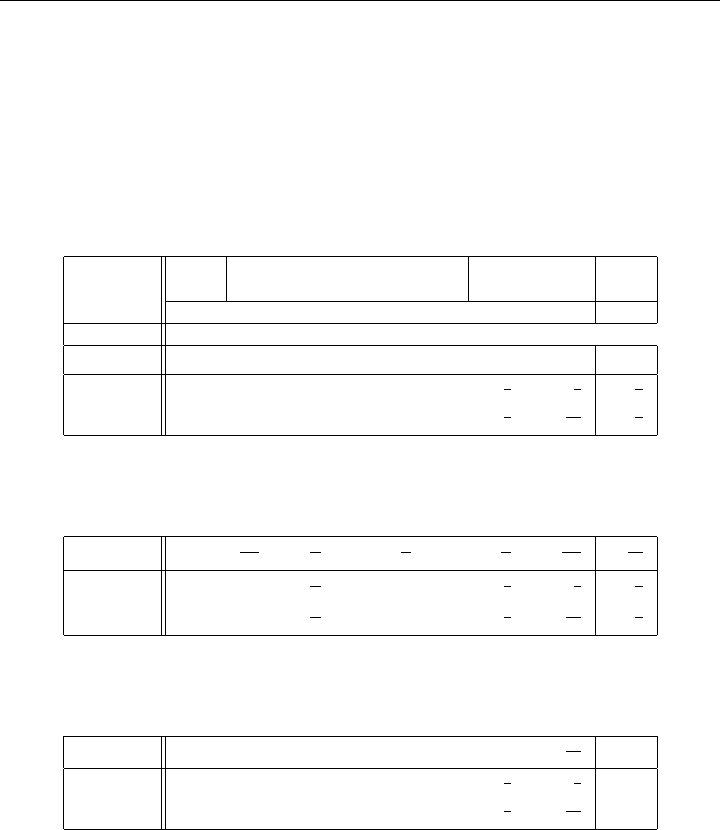
3.5 REVISED SIMPLEX METHOD 95

Iteration 2 (Phase II Start: Introduce z)

Basic OBJ Original Variables Artiﬁcial RHS

Variables Variables

−zx

−z 1 2 1 214 0 0 0

−

−1

Iteration 2 (Phase II: Updated z)¯c

= c

− π

•j

•2

= B

−1

•2

−π

= −c

−1

−z 1

−

−1

Iteration 3 (Phase II Optimal) ¯c

= c

− π

•j

≥ 0

−π

−z 1 3 0 012 1

−4

−

−1

Table 3-7: Revised Simplex Method: Tableau Form Example (Continued)

96 THE SIMPLEX METHOD

(based on Gaussian elimination).

Algorithm 3.3 (Revised Simplex Algorithm) Assume a linear program in standard

form and that x

b is a basic feasible solution and that columns with indices j

,...,j

for a feasible basis B whose inverse B

−1

is known.

1. Simplex Multipliers. Determine the simplex multipliers

π =(B

−1

)

2. Reduced Costs. Determine the reduced costs

¯c

= c

− π

•j

for j nonbasic.

3. Smallest Reduced Cost. Same as Step 1 of the Simplex Algorithm 3.1.

4. Test for Optimality. Same as Step 2 of the Simplex Algorithm 3.1.

5. Incoming Variable. Same as Step 3 of the Simplex Algorithm 3.1.

6. Determine

•s

, the representation of A

•s

in terms of the basis B.

7. Test for unbounded z. Same as Step 4 of the Simplex Algorithm 3.1.

8. Outgoing Variable. Same as Step 5 of the Simplex Algorithm 3.1.

9. Pivot on ¯a

in the matrix



b, B

−1

•s



to obtain



updated

b, updated B

−1



where e

is the unit vector with 1 in row r and zeros elsewhere.

10. Set j

= e

and return to Step 1 with updated

b and B

−1

 Exercise 3.27 Show that pivoting on ¯a

involves multiplying

b, B

−1

, and

•s

by the

inverse of the elementary matrix

= I +(

•s

− e

which is

−1

= I −

(

•s

− e

¯a

3.5.4 COMPUTATIONAL REMARKS

In the standard Simplex Method we modify on each iteration the entire tableau

of (m + 1)(n + 1) entries. Not counting the identity part of the standard sim-

plex tableau, the number of operations (multiplication and addition pairs) on each

iteration is



(n − m)+1



(m +1)=(n − 2m)(m +1)+(m +1)

. (3.65)

In the Revised Simplex Method, we never explicitly compute all of

A. We only

compute

•s

and ¯c; and update −π, and

−1

by pivoting. Thus we modify only

(m + 1)(m + 1) entries of the tableau (including the computation of π). Thus,

starting with an m × n system in a feasible canonical form, the total number of

operations required per iteration is

f(n − m)(m +1)+fm(m +1)+(m +1)

= fn(m +1)+(m +1)

, (3.66)

3.6 NOTES & SELECTED BIBLIOGRAPHY 97

where f is the fraction of nonzero coeﬃcients in the original tableau, which we

assume, on the average, is the same as that in the column entering the basis. The

three terms on the left are the numbers of operations used (a) in “pricing out,”

(b) in representing the new column, and (c) in pivoting.

Comparing (3.66) and (3.65) it is easy to see that the Revised Simplex Method

requires less work than the standard Simplex Method if f, the fraction of nonzeros,

satisﬁes

f<1 − 2m/n.

From the above it is clear that for the Revised Simplex Method to require less work

than the standard Simplex Method we must have n>2m.

3.6 NOTES & SELECTED BIBLIOGRAPHY

Since the invention of the Simplex Method by one of the authors (George Dantzig) in 1947,

numerous papers have appeared; they are far too many to reference all the titles of the

papers and presentations of linear programming.

On ﬁrst glance it may appear that most problems will be nondegenerate. After all,

what is the probability of four planes in three space meeting in a point (for example)! It

turns out that although it appears that the probability of a linear program being degenerate

is zero, almost every problem encountered in practice is highly degenerate. Degeneracy is

the rule, not the exception! For this reason, the choice of the variable to leave the basis in

the case of a tie has been and continues to be the subject of much investigation because of

the theoretical possibility that a poor choice could lead to a repetition of the same basic

solution after a number of iterations. In Linear Programming 2, several examples are given

where using the standard rules results in a sequence of pivots that repeats, called cycling

in the Simplex Algorithm. The choice of pivots under degeneracy and near degeneracy

is examined in detail later, in Linear Programming 2. There proofs are provided for

ﬁnite termination of the simplex algorithm under various degeneracy-resolving schemes

such Dantzig’s inductive method, Wolfe’s rule, Bland’s rule, Harris’s procedure, and the

Gill, Murray, Saunders, Wright anticycling procedure. A proof of convergence in a ﬁnite

number of steps under the random choice rule can be found in Dantzig [1963]; see also

Linear Programming 2.

Another question is concerned with the number of iterations required to solve a linear

program using the Simplex Method. Examples have been contrived by Klee and Minty

[1972] that require in the worst case (2

− 1) iterations. Consider the linear program

Minimize



j=1

−10

m−j

subject to



i−1



j=1

i−j



+ x

+ z

= 100

i−1

, for i =1,...,m,

≥ 0,z

≥ 0, for j =1,...,m.

(3.67)

If we apply the Simplex Method (using the largest coeﬃcient rule) to solve the prob-

lem (3.67), then it can be shown that the Simplex Method performs (2

− 1) iterations

before ﬁnding the optimal solution. If examples such as these are representative of the

98 THE SIMPLEX METHOD

“real-world,” the number of iterations would be too high for the Simplex Method to be

a practical algorithm. Experience solving thousands and thousands of practical problems

shows that the method solves them in surprisingly few iterations. To explain why this

is so requires some way to characterize the special properties of problems encountered in

practice. So far nobody has been able to do so, and the best that one has been able to

do along these lines is to use some hypothesized probabilistic model for generating the

class of linear programs to be solved and proving theorems about the expected number of

iterations. See, for example, Borgwardt [1982a, 1982b, 1987a, 1987b] and Smale [1982]).

In Linear Programming 2 we describe other, more complex, rules for selecting an

incoming column, including those that are scale invariant, that are more computationally

eﬃcient for large problems.

In this chapter, we described a Phase I procedure that uses a full set of artiﬁcial

variables to obtain a starting basic feasible solution; it was ﬁrst proposed by Dantzig

[1951a]. Another technique, labeled the Big-M method, was ﬁrst suggested by Dantzig and

subsequently by others. (See Problems 3.28, 3.29, 3.30, 3.31, and 3.32). The technique was

developed in the context of the standard form, but is also directly applicable to a linear

program with bounded variables. After adding a full set of artiﬁcial variables, the objective

function is modiﬁed by adding to it the sum of the artiﬁcial variables each multiplied by

a large cost M. Then the problem is solved with the new objective function. Provided

the cost M is chosen large enough, it is clear that the artiﬁcial variables will be driven to

zero when minimizing. The problems with this method are (1) M has to be chosen to be

large enough, and (2) a large value of M can cause numerical problems when computing

the multipliers and reduced costs. In Linear Programming 2 we discuss diﬀerent methods

for ﬁnding an initial feasible solution.

The Revised Simplex Method was ﬁrst proposed by Dantzig & Orchard-Hays [1953].

Many excellent books, too numerous to mention, are available on linear programming.

Among them are Bazarra, Jarvis, & Sherali [1990], Bradley, Hax, & Magnanti [1977],

Brickman [1989], Chv´atal V. [1983], Dantzig [1963], Gass [1985], Hillier & Lieberman

[1995], Murty [1983], and Nering & Tucker [1993].

3.7 PROBLEMS

3.1 First solve the following using the Simplex Method. Next solve it using the

Revised Simplex Method. Finally, solve it using the DTZG Simplex Primal soft-

ware option.

Maximize 3x

+ x

+5x

+4x

= z

subject to 3x

− 3x

+2x

+8x

≤ 50

+6x

− 4x

≤ 40

− 2x

+ x

+3x

≤ 20

and x

≥ 0,x

≥ 0.

3.7 PROBLEMS 99

3.2 Consider:

Minimize 3x

− x

= z

subject to x

+ x

−2x

+ x

− x

+ x

and x

≥ 0,x

≥ 0.

(a) Solve the above linear program using the Simplex Method. Be sure to carry

the part of the tableau corresponding to the artiﬁcial variables all the way

to the ﬁnal tableau.

(b) What is the index set (call it B) of the optimal basis? What is A

•B

? Where

is [A

•B

]

−1

in the ﬁnal tableau?

•B

]

−1

)

. Where is π in the ﬁnal tableau? Verify through

direct computation that ¯c = c − A

π.

3.3 Solve the following bounded variable linear program by hand.

Minimize −2x

− x

= z

subject to 3x

+ x

≤ 9

− 2x

≤ 3

and 0 ≤ x

≤ 1, 0 ≤ x

≤ 8.

3.4 Read each of the following statements carefully and decide whether it is true or

false. Brieﬂy justify your answer.

(a) If a tie occurs in the pivot row choice during a pivot step while solving an

LP by the Simplex Method, the basic feasible solution obtained after this

pivot step is degenerate.

(b) In solving an LP by the Simplex Method, a diﬀerent basic feasible solution

is generated after every pivot step.

total number of diﬀerent bases is ﬁnite.

3.5 A farm is comprised of 240 acres of cropland. The acreage to be devoted to

corn production and the acreage to be used for oats production are the decision

variables. Proﬁt per acre of corn production is $40 and the proﬁt per acre

of oats production is $30. An additional resource restriction is that the total

labor hours available during the production period is 320. Each acre of land

in corn production uses 2 hours of labor during the production period, whereas

production of oats requires only 1 hour. Formulate an LP to maximize the

farm’s proﬁt. Solve it.

3.6 Suppose we are solving the problem

Minimize c

subject to Ax = b

x ≥ 0.

and we arrive at the following Phase II tableau:

(−z) 010c

0 110a

0 0 −21a

100 THE SIMPLEX METHOD

(a) Identity the current basic solution and give conditions that assure it is a

basic feasible solution.

(b) Give conditions that assure that the basic solution is an optimal basic

feasible solution.

basic feasible solution.

(d) Give conditions that guarantee that the objective value is unbounded below.

(e) Assuming the conditions in (d) hold, exhibit a feasible ray on which the

objective value goes to −∞ and exhibit a set of infeasibility multipliers for

the dual problem. Note that the ray generated by q ∈

is the set of

points {x | x = θq } as the scalar parameter θ varies from 0 to +∞.

(f) Assuming the conditions of (a) hold, give all conditions under which you

would perform a pivot on the element a

3.7 Late one night, while trying to make up this problem set, your trusty course

assistant decided to give you the following linear program to solve:

RHS

100000111 1 14

010000 2 2−1 −356

001000223 0 04

000100−304566

000010−93−30−1 9

000001−40−2 −154

000000−5 −8 −5 −6 −7 0

After pivoting with the Simplex Algorithm until he got an optimal solution,

he then—klutz that he is—spilled his can of Coke over the ﬁnal tableau (not a

suggested practice). Unfortunately, by Murphy’s Law of Selective Gravitation

(i.e., objects fall where they do the most damage) the spilled Coke dissolved the

right-hand side (RHS) of the ﬁnal tableau, leaving only:

RHS

43/24 1/24 −15/16 −1/30010−115/48 0 1 −

3/81/8 −5/16 00000−11/16 0 1 −

−43/24 1/823/16 1/30001 187/48 0 0 −

5/8 −1/8 −3/16 00000 3/1610−

175/85/8 −209/16 −41000−591/16 0 0 −

71/12 −7/12 −19/8 −4/30100−191/24 0 0 −

107/2 10000 21/200−

Luckily the course assistant was able to ﬁll in the missing right-hand side (opti-

mal basic feasible solution and ﬁnal objective value) without doing any further

pivoting. How did he do it? What is the missing right hand side?

3.8 Spaceman Spiﬀ hurtles through space toward planet Bog. Cautiously, he steps

out of his spacecraft and explores the dunes. Suddenly, the Great Giztnad

pounces! Spaceman Spiﬀ turns his hydroponic laser against it, but it has no

eﬀect! The Great Giztnad rears its gruesome head and speaks: “Solve this

3.7 PROBLEMS 101

problem using the Simplex Method before I return, or I shall boil you in cosmic

oil! Hee, hee, hee!”

RHS

100001121 3 3

01000−1123 4 2

00100 2 5−40 2 4

000101311 2

00001543−21

00000−3 −22−1 −2

Using what he learned in OR340, Spiﬀ quickly applied the Simplex Method and

arrived at the ﬁnal tableau

RHS

100 −100−21012

010−13/74/70−16/713/706/7 13/7

001−4/7 −2/70 15/7 −38/704/7 18/7

000 5/7 −1/70 11/72/719/7 2/7

000 2/71/71 10/75/705/7 5/7

000 11/72/70 27/731/7010/7 17/7

“I have solved the problem, your Vileness,” Spaceman Spiﬀ announces. “Good-

bye, oh hideous master of–”

“Not so fast!” booms the Great Giztnad. “You have missed a column. Those

numbers farther oﬀ to the right are the RHS. Also, you copied some of the

numbers incorrectly. I’ll give you ten more minutes. Solve this quickly, before I

lose my patience and eat you raw!”

RHS

1000011213 3

∗

01000−11234 2

∗

155

∗

00100 2 5−402 4

∗

0001013117

∗

00001543−27

∗

00000−3 −22−1 −2 −2

∗



∗

represents changes from the original tableau



Show what the resulting ﬁnal tableau and optimal solution will be, and explain

why it is optimal. Hint: You do not need to redo the Simplex Method.

3.9 Consider the following linear program:

Minimize 2x

− x

+ x

+5x

= z

subject to x

+ x

+3x

− 4x

+2x

≤ 5

+2x

− 5x

+ x

≥ 2

≥ 0,j=1,...,4.

(a) Use the Simplex Method (with no more than 2 artiﬁcial variables) to show

that it is infeasible.