Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

182 PRICE MECHANISM AND SENSITIVITY ANALYSIS

a list of the various processes available in the plant and their input and output

coeﬃcients. Somewhat confused by this mass of data, the civil servants who were

supposed to operate the plant decide to call in a private industrialist to consult on

how they should plan their production. The industrialist realizes that it would be

good training for his men and a feather in his cap if he could contract to actually

operate the plant. Accordingly, once he gets the information and studies the data,

he proposes a ﬂat fee for which he will manage the plant, turn over to the government

the required amounts of output, and use no more than the allotted quantities of the

scarce materials. The civil service men declare that all other things being equal,

they think it would be best for the government to operate the plant, but if he can

convince them that his proposal is a good one (meaning that if the government

operates the plant, it is unlikely it could do so less expensively), they will accept

his oﬀer.

The industrialist takes the data back to his oﬃce, gets out his linear program-

ming book titled Linear Programming 1: Introduction, and uses input-output coef-

ﬁcient data to form a matrix A and a labor cost vector c.

To determine the minimum fee for which he can aﬀord to operate the defense

plant, the industrialist has only to solve the following linear program:

x = z (min),

Ax = b,

x ≥ 0.

(7.28)

Using the software provided, he quickly solves the problem on his PC and prints

out the results using his printer. The results are that z

∗

is the minimum cost and

∗

is the vector of optimal process utilization levels. His ﬁrst thought is to explain

the linear programming technique to his civil service friends, show them the ﬁnal

tableau, and thereby convince them that they can do no better than to accept

his oﬀer and pay him z

∗

. But then he realizes that this plan will give away his

secret; the civil servants will have no further need for him. They will take his vector

of operating levels x

∗

to optimally operate the plant themselves. To prevent this

from happening, he must ﬁnd a way to convince the government that z

∗

is minimal

without giving away his plan x

∗

To this end, he decides to invent a system of prices that he will oﬀer to pay for

the materials, provided he is paid certain prices for the outputs. He wants these

prices to be such that there are no proﬁts on any individual activity, for if there

were proﬁts, the government would spot them and know that they could ﬁnd a way

to run the plant with lower labor cost. On the other hand, given these restraints,

he wants to make as much money as possible. That is, he wants his price vector π

to satisfy

b = v (max),

π ≤ c.

(7.29)

He recognizes this problem as the dual of the one he just solved and immediately

produces the dual solution: optimal π = π

∗

, the simplex multipliers from the last

iteration of the Simplex Method used to solve the primal problem, and maximal

v = v

∗

. Fortunately, he notes with relief, v

∗

= z

∗

7.2 INTRODUCING A NEW VARIABLE 183

With these results under his arm, the industrialist goes back to see the civil

servants and presents his oﬀer in price terms. The bureaucrats check to be sure

that every one of the inequalities (7.29) is satisﬁed, and, of course, calculate the

total cost using these prices: b

∗

= v

∗

. The industrialist then invites them to

consider any program x satisfying (7.28). Its cost to them, if they operate the plant

themselves, is c

x. But replacing π by π

∗

in (7.29) and multiplying both sides by

any feasible x yields

(π

∗

)

Ax ≤ c

x (7.30)

or, by (7.28),

(π

∗

)

b ≤ c

x. (7.31)

Hence,

∗

≤ c

x, (7.32)

so that the cost of any feasible program that the bureaucrats could devise will be

at least v

∗

. This argument convinces the civil servants that they can do no better

than to accept the industrialist’s ﬂat fee oﬀer of v

∗

. With one last hope of operating

the plant themselves, they try to pry out of him just how much of each process he

intends to operate; but he feigns ignorance of such details and is soon happily on

his way with a signed contract in his pocket.

7.1.5 SIGN CONVENTION ON PRICES

Economists use the sign convention that the ﬂow of items produced by an activity

are positive and the ﬂow of items consumed by an activity are negative. They

also assume the value of the cost item has a price of unity and that costs (money

paid out) are being minimized. With this in mind, let us introduce into the linear

program a ﬁctitious “procurement” activity j = n + i that increases the allotment

of item i; its coeﬃcients are zero except for unity in row i and c

n+i

in the cost row.

How low must the cost c

n+i

be before it pays to increase the allotment of item i ?

Pricing out this activity, we see that it pays if

n+i

<π

Hence, π

is the break-even cost of the item i procurement activity.

If an item is produced by an activity a

> 0 and if the item has value, then the

ﬂow of money π

> 0 is toward the activity. Similarly, for each unit of activity

j, the input a

< 0 would induce a payment of π

< 0. In other words, the ﬂow

of money is out.

The total ﬂow of money into the activity by the price device is given by pricing

it out, that is,



i=1

If this value exceeds c

, the amount that would be received by the alternative of

direct payment, then this activity (or some other with the same property) will be

used in lieu of a basic activity now in use. This in turn will generate a new set of

prices, etc.

184 PRICE MECHANISM AND SENSITIVITY ANALYSIS

Basic Admissible Variables (Including Slacks) Constants

Variables −zx

−z 1 −12 −20 −18 −4000 0

04971010 6

01134001 4

Table 7-1: Initial Tableau for Sensitivity Analysis

7.2 INTRODUCING A NEW VARIABLE

After an optimal solution x = x

∗

has been determined, suppose that we want to

examine the eﬀect on the optimal solution of introducing a new variable x

n+1

with

cost coeﬃcient c

n+1

and input-output coeﬃcients A

•n+1

LP IN STANDARD FORM

The augmented problem is then

Minimize c

x + c

n+1

= z

subject to Ax + A

•n+1

n+1

= b

x ≥ 0

n+1

≥ 0.

(7.33)

Introducing a new variable into (7.1) as shown in (7.33) does not alter feasibility

since we can make it nonbasic and set its value to be at its lower bound of 0. Thus,

the current solution is still feasible. However, the solution need not be optimal since

the reduced cost ¯c

n+1

corresponding to the new variable x

n+1

may be negative. In

order to check for optimality we compute

¯c

n+1

= c

n+1

− A

•n+1

∗

. (7.34)

If ¯c

n+1

≥ 0, the old solution with x

n+1

= 0 is optimal. If, on the other hand,

¯c

n+1

< 0, then we know that we can improve on the solution by bringing the

variable x

n+1

into the basis. It may be necessary to perform a series of pivot steps

before optimality is regained.

Example 7.3 (A New Column Introduction) Consider the product mix problem as

stated in Section 1.4.1:

−12x

− 20x

− 18x

− 40x

= z (min)

+9x

+7x

+10x

+ x

= 6 (carpentry)

+ x

+3x

+40x

+ x

= 4 (ﬁnishing)

(7.35)

This is shown in simplex tableau form in Table 7-1. Since this is already in canonical form,

addition of artiﬁcial variables is unnecessary, and we can proceed directly to Phase II of

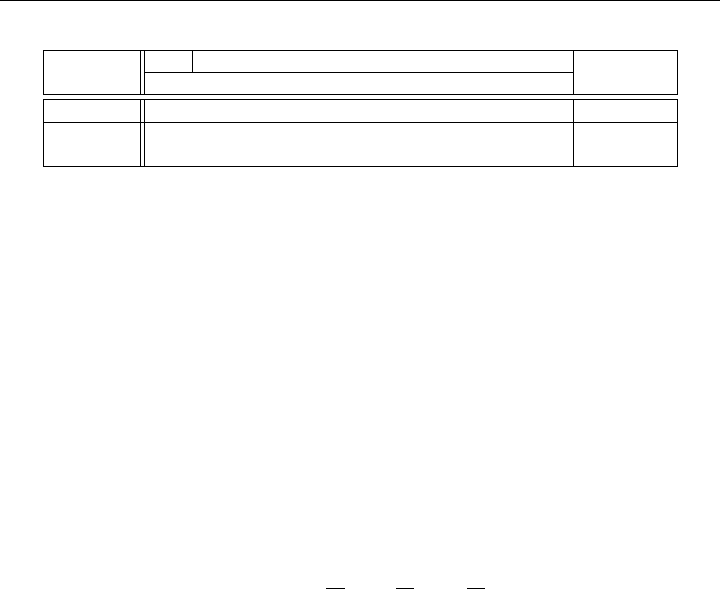
7.2 INTRODUCING A NEW VARIABLE 185

Basic Admissible Variables (Including Slacks) Constants

Variables −zx

−z 10 20/310/30 44/15 4/15 56/3

01 7/35/30 4/15 −1/15 4/3

00−1/30 1/30 1 −1/150 2/75 1/15

Table 7-2: Optimal Tableau for Sensitivity Analysis

the Simplex Method. After several iterations we arrive at the optimum solution as shown

in the ﬁnal tableau in Table 7-2.

From the information contained in this tableau (Table 7-2) we see that the optimum

product mix for the problem as stated in thousands of units is at the rate of 4/3 thousand

desks of type 1 and 1/15 thousand desks of type 4 per time period for a total proﬁt rate

of z = $56/3 thousand per period.

Suppose a new desk called Type 7 has been designed that will require 6 man-hours of

carpentry shop time and 2 man hours of ﬁnishing department labor per desk. Based on an

estimated proﬁt of $18 per desk, we would like to know whether it would pay to produce

this desk.

Note that the negatives of the values of the simplex multipliers, 1, 44/15, 4/15, for

the last iteration can be obtained from the top row vector of the inverse of the ﬁnal basis

(columns corresponding to (−z), x

, and x

). This yields, after pricing out,

¯c

= −18 +

(6) +

(2) =

Since ¯c

> 0, it does not pay to produce this desk.

 Exercise 7.2 If the economic sign convention of Section 7.1.5 is followed, show that

the signs of the bottom two equations of (7.35) are reversed and the optimal prices are

=44/15 and π

=4/15, corresponding to the top row of the inverse in Table 7-1.

BOUNDED VARIABLE LP

Next, let us consider the more general case when x

n+1

has upper and lower bounds

speciﬁed, i.e., l

n+1

≤ x

n+1

≤ u

n+1

, where the lower bound is not necessarily 0 and

the upper bound is not necessarily ∞. In this case, besides regaining optimality,

we also have to be concerned with feasibility. There are three cases to consider:

1. The lower bound l

n+1

= −∞ and the upper bound u

n+1

= ∞. In this

case x

n+1

= 0 provides a feasible solution. However, the solution (if not

degenerate) is not optimal if ¯c

n+1

= 0 because it is proﬁtable to increase x

n+1

if ¯c

n+1

< 0 and to decrease x

n+1

if ¯c

n+1

> 0.

2. The lower and upper bounds are both ﬁnite. We ﬁrst look at easy cases such

as setting set x

n+1

at its lower bound and checking to see whether the solution

found by adjusting the basic variables is feasible. If not, we try again setting

186 PRICE MECHANISM AND SENSITIVITY ANALYSIS

n+1

at its upper bound. If this also does not work, we check to see whether 0

is bracketed by the bounds, in which case we set x

n+1

= 0 to obtain a feasible

solution. See Exercise 7.3.

If a feasible solution is not obtained at either bound of x

n+1

or at x

n+1

=0,

we set x

n+1

= 0 and perform Phase I of the Simplex Method by creating a

Phase I objective and a modiﬁed problem for which this solution is feasible.

If u

n+1

< 0, we set the Phase I objective function to minimize w = x

n+1

and temporarily set u

n+1

= ∞.If0<l

n+1

, we set the Phase I objective

function to be w = −x

n+1

and temporarily set l

n+1

= −∞. If by checking

at each iteration of the Simplex Algorithm to see whether x

n+1

is feasible

with respect to the original bounds a feasible solution is found, we terminate

Phase I, reset the original bounds, and continue with Phase II. If Phase I

terminates optimal with w>0, we report the original problem as infeasible.

This method is called minimizing the sum of infeasibilities.

If a feasible solution is obtained, we compute the value of ¯c

n+1

using equa-

tion (7.34). If x

n+1

= l

n+1

and ¯c

n+1

≥ 0 the solution is optimal, else if

¯c

n+1

< 0, we perform one or more iterations of the Simplex Method. If

n+1

= u

n+1

and ¯c

n+1

≤ 0 the solution is optimal, else if ¯c

n+1

> 0, we per-

form one or more iterations of the Simplex Method. If x

n+1

= 0 is feasible

and ¯c

n+1

= 0 the solution is optimal, else if ¯c

n+1

= 0, we perform one or more

iterations of the Simplex Method.

3. Either the lower bound or the upper bound is inﬁnite but not both; see Ex-

ercise 7.4.

 Exercise 7.3 Show how we can take advantage of the sign of ¯c

n+1

to possibly reduce

the number of computations in Case 2 above.

 Exercise 7.4 For Case 3 above, complete the detailed steps for the case where either

the lower bound or the upper bound is inﬁnite but not both.

7.3 INTRODUCING A NEW CONSTRAINT

We assume that the constraint being introduced is of one of the following forms:

m+1•

x = b

m+1

m+1•

x ≤ b

m+1

m+1•

x ≥ b

m+1

(7.36)

where b

m+1

≥ 0. By setting diﬀerent bounds on the slack variable x

n+1

we can

write any of the constraints (7.36) in the form

m+1•

x + x

n+1

= b

m+1

. (7.37)

7.3 INTRODUCING A NEW CONSTRAINT 187

Thus if the constraint reads “= b

m+1

,” then 0 ≤ x

n+1

≤ 0, if it reads “≤ b

m+1

,”

then 0 ≤ x

n+1

≤∞, and if it reads “≥ b

m+1

,” then −∞ ≤ x

n+1

≤ 0. The cost

n+1

associated with x

n+1

is zero.

The current solution x = x

∗

is feasible, optimal, and satisﬁes Ax

∗

= b for the

original problem. If it also satisﬁes the added constraint (7.37) with x

n+1

= x

∗

n+1

the solution (x

∗

n+1

) is also optimal for the augmented problem, as can be easily

seen by keeping the old optimal prices and setting the price on the extra constraint

to be equal to zero.

But what if the solution x = x

∗

is infeasible after the addition of the constraint?

That is, for the equality constraint, x

n+1

= 0; for the ≤ constraint, x

n+1

< 0; or

for the ≥ constraint, x

n+1

> 0. Then we can solve the infeasibility problem by

minimizing a Phase I objective, and a modiﬁed problem is constructed as follows.

1. For the “= b

m+1

” case, if x

∗

n+1

> 0, then set w = x

n+1

and set u

n+1

= ∞.

On the other hand, if x

∗

n+1

< 0, then set w = −x

n+1

and set l

n+1

= −∞.

2. For the “≤ b

m+1

” case, if x

∗

n+1

< 0, then set w = −x

n+1

and set l

n+1

= −∞.

3. For the “≥ b

m+1

” case, if x

∗

n+1

> 0, then set w = x

n+1

and set u

n+1

−∞.

If by checking at each iteration of the Simplex Algorithm to see whether x

n+1

feasible with respect to the original bounds a feasible solution is found, we terminate

Phase I, reset the original bounds, and continue with Phase II. If Phase I terminates

optimal with w>0, we report the original problem as infeasible. This method is

called minimizing the sum of infeasibilities.

The new multipliers (π, π

m+1

) can be easily computed from



B 0





m+1











m+1







(7.38)

where θ =1ifw = x

n+1

and θ = −1ifw = −x

n+1

, and, letting j

,... ,j

be indices of the variables in the optimal basis B of the original problem, v

m+1,j

,... ,a

m+1,j

)

. It is easy to see that the solution is given by

m+1

= θ and π = θ(B

−1

)

. (7.39)

The reduced costs can be easily obtained from

d = d

− ( N

)



m+1



= −( N

)



m+1



, (7.40)

where v

=(a

m+1,j

m+1

m+1,j

m+2

, ..., a

m+1,j

)

and j

m+1

,...,j

are the

indices of the nonbasic variables.

188 PRICE MECHANISM AND SENSITIVITY ANALYSIS

 Exercise 7.5 Show that



B 0



−1



−1

−v

−1



Derive the inverse form by using Equation (A.21) on Page 330.

7.4 COST RANGING

Often costs are uncertain in industrial applications. For example, in the oil industry,

the spot prices for purchasing crude oils for making gasoline may have changed after

the linear program has been run, and we are concerned with whether the changes

in price are suﬃcient to require us to rerun the program. It is clear that changing

the costs does not aﬀect feasibility, and thus we only need to be concerned with

optimality. Cost ranging refers to the determination of the range of costs for a

variable x

such that the solution stays optimal. We are going to consider only

two cases: the eﬀect of changing the cost of one nonbasic variable and the eﬀect of

changing the cost for one of the basic variables.

THE EFFECT OF NONBASIC-VARIABLE COST

CHANGE

Consider the nonbasic variable x

with cost c

. For optimality to hold we need the

reduced costs to be nonnegative. That is, we need

≥ A

•s

∗

. (7.41)

Thus, the range of costs c

for the nonbasic variable x

over which optimality of the

basis B is preserved is c

≥ A

•j

∗

Example 7.4 (Change in Nonbasic Cost) In Example 7.3 on page 184, how much

would the proﬁt for desk Type 7 have to change before it becomes worthwhile to produce

it? It follows from (7.41) that if the cost coeﬃcient c

for any nonbasic activity is decreased

by the value of its relative cost factor ¯c

in the optimal solution, it becomes a candidate to

enter the basis. In this case, desk Type 7 becomes a candidate for production if its proﬁt

per unit can be increased by ¯c

=2/15.

 Exercise 7.6 How much must the proﬁt on desk Type 2 be increased to bring it into

an optimum solution? How much would you have to raise the selling price on desk Type 3

in order to make its production optimal? How would you modify the model if as the result

of a market survey you have determined that the amount that can be sold is a function of

selling price and that there is an upper bound on the amount that can be sold?

7.4 COST RANGING 189

THE EFFECT OF BASIC-VARIABLE COST CHANGE

The determination of the range of costs over which optimality of the basis is pre-

served is slightly more complicated in this case. For convenience, let us suppose that

the cost of optimal basic activity j

is changed from c

to γ and we are interested

in how much γ must increase or decrease before the basis B is no longer optimal.

The basic cost vector c

changes to

(γ)=c

+(γ − c

, (7.42)

where e

is the rth column of the identity matrix. Then the new multipliers π are

now a function of γ, which we write as π(γ). By deﬁnition, B

π(γ)=c

(γ), that

is,

π(γ)=c

+(γ − c

. (7.43)

Then for the current solution to remain optimal, we need

˜c

(γ)=c

− π(γ)

•j

≥ 0 for all nonbasic j. (7.44)

The inequalities (7.44) are all linear in γ, because multiplying (7.43) on the left by

)

−1

, and noting that (B

)

−1

)=(B

−1

)

,wehave

π(γ)=π

∗

+(γ − c

)(B

−1

)

. (7.45)

From these we can compute a range of values on γ that maintain optimality of the

solution.

Therefore, the new reduced costs are given by

˜c

(γ)=c

− A

•j

π(γ)=c

− A

•j

∗

− (γ − c

•j

−1

)

= c

− A

•j

∗

− (γ − c

)(B

−1

•j

)

=¯c

− (γ − c

)

•j

=¯c

− (γ − c

)¯a

. (7.46)

As long as ˜c

(γ) ≥ 0 for all nonbasic j, the solution will remain optimal. The range

of γ for which the solution is optimal can be computed by setting ˜c

(γ) ≥ 0 for each

nonbasic j and solving for γ. Thus, the range on γ is given by

+ max

¯a

¯c

¯a

≤ γ ≤ c

+ min

¯a

¯c

¯a

. (7.47)

As long as γ lies in the range deﬁned by (7.47), the current basis B remains

optimal; however, the optimal value of the objective function changes according to

z(γ)=c

(γ)x

∗

= c

∗

+(γ − c

∗

= z

∗

+(γ − c

, (7.48)

where x

∗

is the current optimal solution.

190 PRICE MECHANISM AND SENSITIVITY ANALYSIS

Example 7.5 (Change in Basic Cost) For what range of cost of a particular basic

activity j

= 1 in the desk production Example 7.3 does the present optimal solution still

remain optimal? The present solution will remain optimal as long as cost coeﬃcient γ = c

satisﬁes Equation (7.47). Hence, based on (7.47) we use Table 7-2 to ﬁrst compute

min

¯a

¯c

¯a

= min

¯c

¯a

¯c

¯a

¯c

¯a



20/3

7/3

10/3

5/3

44/15

4/15



=2,

max

¯a

¯c

¯a

= max

¯c

¯a



4/15

−1/15



= −4.

Thus from (7.47) we see that the present solution remains optimal for c

in the range

−12 − 4 ≤ c

≤−12 + 2, where −12 was the original value of c

 Exercise 7.7 For what range of proﬁt for desk Type 4 is the present solution (see

Table 7-2) still optimal? Determine what activity enters the solution if c

is decreased to

−20, increased to −19/2. What activity leaves the solution in each case?

 Exercise 7.8 Construct an example by changing b

in the original problem in Table 7-1

to show that if the proﬁt for desk Type 1 is decreased to 19/2, i.e., c

is increased to −19/2,

then desk Type 1 is not the one that leaves the solution.

 Exercise 7.9 Given an initial optimal basic feasible solution, prove the theorem that

reducing the cost of a basic activity will not necessarily cause it to be dropped from the

optimal solution. Verify this by showing, in the example of Exercise 7.7, that no matter

how much c

is decreased, activity j = 1 will still remain in the basis.

 Exercise 7.10 Modify the cost ranging analysis for the case when x has both upper

and lower bounds associated with it.

7.5 CHANGES IN THE RIGHT-HAND SIDE

It is important to be able to examine the eﬀect of changes to the right-hand side

of the constraints, especially those that specify what resources are available. For

example, the availability of a resource may be constrained as a result of a company’s

policy decision to place a quota on imports of an item from a foreign company.

Assume that we have an optimal solution to a linear program in standard form.

Let the right-hand side of the rth constraint be given by a parameter θ with a

particular value of θ being the current b

. Let

b(θ)=b +(θ − b

, (7.49)

where e

is the rth column of the identity matrix. If the value of θ does not make

the current basis infeasible, then the revised basic solution is still optimal. However,

7.5 CHANGES IN THE RIGHT-HAND SIDE 191

if it is infeasible, this will result in a change of basis requiring that the new problem

be solved by a Phase I / Phase II procedure or by the Dual-Simplex Method. (The

Dual-Simplex Method is a pivot procedure that uses diﬀerent rules as to which

column leaves the basis and which enters the basis. It turns out in reality to be a

clever way to solve the dual of the original problem by the Simplex Method without

having to transpose the matrix.) The range of values θ for the right hand side of

the rth constraint, for which the current basis remains feasible and thus optimal, is

obtained by ensuring that the solution x

(θ)to

(θ)=b(θ) (7.50)

is such that x

(θ) ≥ 0. From (7.49) and (7.50) we get

(θ)=B

−1

b +(θ − b

−1

= x

∗

+(θ − b

−1

, (7.51)

where x

∗

is the optimal solution with θ = b

. For feasibility we need x

(θ) ≥ 0,

thus the range of θ is

+ max

−(x

∗

)

≤ θ ≤ b

+ min

−(x

∗

)

, (7.52)

where β

is element (i, r)ofB

−1

As long as θ lies in the range deﬁned by (7.52), the current basis B remains

optimal; however, the optimal values of the optimal basic solution (7.51) change,

and the optimal value of the objective function changes according to

z(θ)=c

(θ)=c

∗

+(θ − b

= z

∗

+(θ − b

)π

∗

, (7.53)

where z

∗

is the current optimal objective value and π

∗

are the simplex multipliers

of the current optimal solution.

 Exercise 7.11 Derive the relation (7.53) alternatively by noting that z(θ)=b(θ)

∗

Example 7.6 (Change in Capacity) What is the eﬀect of increasing ﬁnishing depart-

ment capacity in Example 7.3? The present solution will remain optimal as long as the

right-hand side θ = b

satisﬁes (7.52). Hence, based on (7.52) we use Table 7-2 to ﬁrst

compute

max

−(x

∗

)

= max



−x





−1/15

2/75



= −2.5,

min

−(x

∗

)

= min



−x





−4/3

−1/15



=20.

Thus from (7.52), we see that the present solution remains feasible and optimal for b

the range 4 − 2.5 ≤ b

≤ 4 + 20, or 1.5 ≤ b

≤ 24, where 20 was the original value of b

Thus, the answer to our question is that we can increase ﬁnishing department capacity up

to 20,000 hours. The net proﬁt per hour of increase is −π

∗

=$4/15.