Dantzig G., Thapa M. Linear programming. Vol.1. Introduction

Подождите немного. Документ загружается.

162 EQUIVALENT FORMULATIONS

6.8 NOTES & SELECTED BIBLIOGRAPHY

Goal Programming is a special case of solving multiple objectives in general. Additional

information on goal programming can be found in Davis & McKeown [1981], Hillier &

Lieberman [1995], Ignizio [1976], Lee [1972], Murty [1983], and Steuer [1985]. For ap-

plications of goal programming to ﬁnancial management see, for example, Sponk [1981].

Techniques for formulating linear programs in practice can be found in Bradley, Hax, &

Magnanti [1977], Shapiro [1984], and in Tilanus, DeGans, & Lenstra (eds.) [1986].

Curve ﬁtting is used extensively, especially in statistical applications. In statistics, the

method described in Section 6.6 is referred to as least-squares or multiple linear regression.

Many excellent references are available, for example, Chambers [1977], Feller [1957, 1969],

Kennedy & Gentle [1980], and Mood, Graybill, & Boes [1974]. See Linear Programming 2

for a discussion on the use of the QR factorization to solve the linear least-squares problem.

The proof of Exercise 6.1 is originally due to Tucker (see, Dantzig [1963]). Problem 6.10

on page 165 introduces the concept of a ﬁxed charge problem, see Dantzig & Hirsch [1954].

Problem 6.12 on page 166 brieﬂy introduces the concept of game theory, the mathematical

formulation of which can be found in Borel [1921, 1924, 1927], von Neumann [1928, 1937,

1948a, 1953], and in the now famous book Theory of Games and Economic Behavior by

von Neumann & Morgenstern [1944].

6.9 PROBLEMS

6.1 Consider the following linear program:

Minimize −2x

+ x

= z

subject to x

+ x

− x

≥ 3

−∞ ≤ x

≤∞,x

≥ 0,x

≥ 0.

(a) Replace the variable x

by the diﬀerence of two nonnegative variables and

solve the resulting linear program by hand.

(b) Solve the linear program using the DTZG Simplex Primal software option.

6.2 Formulate the following problem as a linear program in standard form:

Minimize x

− 3x

+ x

− x

= z

subject to x

− 2x

− 3x

+ x

≤ 10

+ x

− 2x

≤ 6

unrestricted,x

≥ 0,x

≥ 0.

(a) Replace each of the unrestricted variables x

and x

by the diﬀerence of

two nonnegative variables and solve the resulting linear program by hand.

(b) Solve the linear program using the DTZG Simplex Primal software option.

6.9 PROBLEMS 163

6.3 Formulate the following problem as a linear program and solve it using the DTZG

Simplex Primal software option.

Minimize 2|x

| +3x

+4x

= z

subject to x

+ x

+2x

≤ 8

− x

+ x

≥ 4

unrestricted,x

≥ 0,x

≥ 0.

6.4 Formulate the following problem as a linear program and solve it using the DTZG

Simplex Primal software option.

Minimize −6x

− 8x

− 5x

− 4x

= z

subject to 3x

+3x

+8x

+2x

=50

|2x

+3x

+2x

|≤20

≤ 40, for j =1,...,4.

What happens if the bounds x

≤ 40 are dropped.

6.5 Where possible, reformulate the following problems as linear programs in stan-

dard form, min c

x, Ax = b, x ≥ 0.

(a)

Minimize c

x = z, with c>0

subject to x

= max(u

),j=1,...,n.

(b)

Minimize c

x = z

subject to A

x ≥ 0

x ≤ 0.

(c)

Minimize c

x = z

subject to Ax = b

x ≥ 0

integer for j =1,...,n.

(d)

Minimize c

x = z

subject to Ax = b

x ≥ 0

x =0.

6.6 Excesses and Shortages. Problems that occur in practice often have costs as-

sociated with coming below or exceeding certain requirements. For example, if

production of an item is below the contracted amount, a shortage cost is in-

curred either because of the contract stipulation or because the demand is met

by having to buy the item from an expensive outside source. On the other hand,

if production exceeds the demand, then a holding cost is incurred for having to

store the excess production.

164 EQUIVALENT FORMULATIONS

Suppose that your company manufactures n diﬀerent items x

, each of which

can be sold at a unit proﬁt of p

. Assume that the production constraints are

Ax = b. Except for item 1, assume that all other items, x

,... ,x

, can

be sold easily on the open market. Suppose that your contractual agreements

are such that you must deliver d

units of item 1. If you are unable to deliver

exactly d

units of item 1, a penalty cost, or shortage cost, of s is incurred. On

the other hand, in the hopes of selling item 1 in the next time period, if you

produce more than the demand, you incur a holding cost, or excess cost, of e.

Develop a linear programming model to maximize proﬁt. Clearly state the

conditions under which the linear programming model succeeds in solving this

problem.

6.7 Use the DTZG Simplex Primal software to ﬁnd the maximum of the minimum

value of x

for j =1,...,3 that satisfy the system of inequalities

+ x

+2x

≤ 15

+3x

+4x

≤ 25

+ x

+5x

≤ 30

≥ 0,j=1, 2, 3.

6.8 Use the DTZG Simplex Primal software option to ﬁnd the maximum of the

minimum value of x

for j =1,...,3 that satisfy the system of inequalities

+ y

+3y

≥ 5

+3y

+1y

≥ 10

+4y

+5y

≥ 20

≥ 0,j=1, 2, 3.

6.9 Optical Scanning Problem (Avi-Itzhak, H., Van Mieghen, J., & Rub, L. [1993]).

An optical scanner compares the preprogrammed pattern of each letter, de-

scribed by a matrix of pixels 50 × 50 = 2500 recorded as a 2500 dimensional

vector normalized to be of unit length, with that of an unknown letter observed

by scanning a matrix of pixels 50 ×50 = 2500. The unknown letter described by

the vector x will be said to be the same as the preprogrammed letter described

by the vector a if the correlation

||x||

≥ k,

where k is a constant typically chosen to be greater than say 0.95.

(a) Suppose that you are designing software for a scanner to be used to diﬀeren-

tiate between the several kinds of letters of an alphabet and the typefaces of

each letter. Then each unknown would need to be compared with several

preprogrammed versions of each letter, which unfortunately turns out to

take too long to do and requires too much storage. Instead, we would like

to use some sort of average representation of each letter in order to reduce

the processing time and storage. If we let a

= A

i•

, i =1,...,m, represent

m diﬀerent representations of a given letter, then we might be interested in

choosing as the “average” representation of typefaces of a letter as β = β

∗

of unit length, that maximizes the minimum correlation:

ρ = max



min

i=1,...,m

i•

||β||



, ||β|| =1. (6.23)

6.9 PROBLEMS 165

Show that this is equivalent to solving the following quadratic program (i.e.,

an optimization problem where the objective function is a quadratic and

the constraints are linear):

Minimize y

y = z

subject to A

i•

y ≥ 1,i=1,...,m,

(6.24)

and setting β = y/||y||. Hint: Show that (6.24) is equivalent to ﬁnding β

that solves

Maximize ρ = u

subject to ρ ≤

i•

||β||

,i=1,...,m.

(b) If software for solving a quadratic program is unavailable, show how you

can apply piecewise linear approximations to solve the quadratic program

(6.24) approximately as a bounded variable program. Hint: Show that y

is a separable quadratic form.

6.10 Fixed Charge Problem. In many practical applications there is the underlying

notion of a ﬁxed charge. For example, a reﬁnery may want to know whether

building an additional reﬁnery would result in better serving the current set of

customers. In such situations the cost is characterized by

c =



αx + β if x>0,

0ifx =0,

where β is the ﬁxed charge.

(a) Show that we may model this by writing the cost form as

c = αx + βy

and including the constraints

y = {0, 1}

and

x − yU ≤ 0,

where U is an upper bound on x.

(b) The inclusion of integer variables in the formulation requires a special-

purpose solver. However, if only one or two variables have an associated

ﬁxed charge, it is possible to use the DTZG Simplex Primal option to solve

the problem. Discuss how you would do this.

ment has the possibility of a special order on a new desk 5 that requires

12 carpentry hours, 50 ﬁnishing hours, and generates a proﬁt of $60. Unfor-

tunately, it requires some additional equipment for ﬁnishing purposes and

the cost of this equipment is $500. Should desk 5 be manufactured. What

if the cost of the new equipment was $1,000.

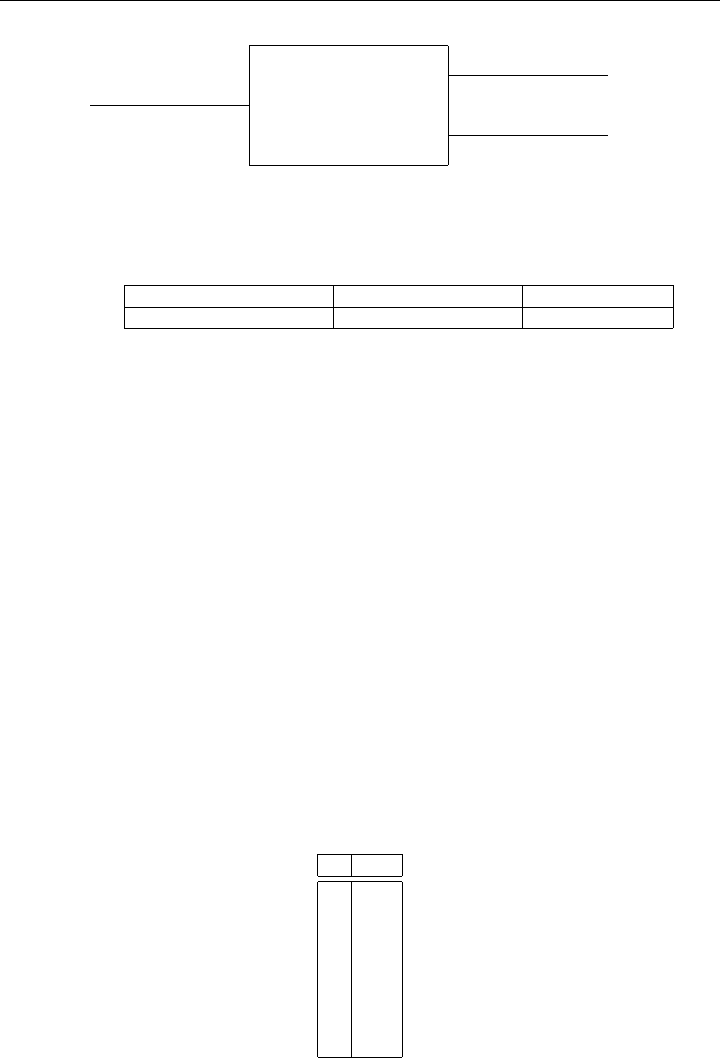
166 EQUIVALENT FORMULATIONS

-



500



Gallons of raw milk

Cost in

cents/gallon

Figure 6-4: Purchase Price of Raw Milk in Region A

6.11 (a) Consider the linear program

Minimize 1x

+2x

+3x

= z

subject to 2x

− x

+3x

0 ≤ x

≤ 2, for j =1, 2, 3,

where all variables must take integer values. Show how to convert this to

a binary integer program where all the variables are either 0 or 1 and the

coeﬃcients and right-hand sides are −1, 0, or +1.

(b) Generalize to a linear program where all the variables must take integral

values and all the coeﬃcients and right-hand side are integers.

6.12 Game Theory. In a zero-sum matrix game, the row player, to ﬁnd his optimal

mixed strategy, must solve the linear program

Maximize L

subject to A

x ≥ Le

x =1,

and the column player, to ﬁnd her optimal strategy, must solve the linear pro-

gram

Minimize M

subject to Ay ≤ M ˆe

ˆe

x =1,

where A is m × n, e =(1, 1,...,1)

is of dimension m, and ˆe =(1,...,1)

of dimension n. Prove that these two programs are duals of each other and

Max L = Min M = v. Note: v is called the value of the game.

6.13 Ph.D. Comprehensive Exam, September 23, 1972, at Stanford. Happy Milk

Distributors (HMD) purchases raw milk from farmers in two regions: A and

B. Prices, butterfat content, and separation properties of the raw milk diﬀer

between the two regions. HMD processes the raw milk to produce cream and

milk to desired speciﬁcations for distribution to the consumers.

Region A Raw Milk. The purchase price in 1972 dollars of raw milk in Region

A is indicated in Figure 6-4. For example, to purchase 700 gallons would cost

54(500) + 58(200) cents. There is no upper bound on the amount that can be

purchased. Raw milk from Region A has 25% butterfat and when separated (at

6.9 PROBLEMS 167

Separation of

Region A Milk

Raw Milk

15% butterfat

Milk

41% butterfat

Milk

12% butterfat

Figure 6-5: Separation of Region A Milk

-



700



Gallons of raw milk

Cost in

cents/gallon

Figure 6-6: Purchase Price of Raw Milk in Region B

5 cents per gallon) yields two “milks,” one with 41% butterfat and another with

12% butterfat; this is shown in Figure 6-5. The volume of milk is conserved in

all separation processing.

Region B Raw Milk. The purchase price in 1972 dollars (as for Region A raw

milk) is illustrated in Figure 6-6. Raw milk from Region B has 15% butterfat

and when separated (at 7 cents per gallon) yields two “milks,” one with 43%

butterfat and another with 5% butterfat; this is shown in Figure 6-7. The

volume of milk is conserved in all separation processing.

Production Process. After the milk is purchased and collected at the plant, it is

either mixed directly or separated and then mixed. Mixing, to produce cream

and milk to speciﬁcations, is done at no cost. For example, some of the raw

milk from Region A may be separated and then mixed, and some of it may be

mixed directly (i.e., without having been ﬁrst separated).

Demand and Selling Price. The demand and selling price are described in Ta-

ble 6-2. For example, all the cream produced must have at least 40% butterfat;

it sells at $1.50 per gallon; no more than 250 gallons of the cream produced can

be sold.

The Problem. Assuming disposal is free, formulate a linear program that when

solved on a computer would enable HMD to maximize its proﬁts.

6.14 Vajda [1961]. Suppose that you visit the racecourse with B dollars available

for betting. Assume further that there is only one race on this day and that N

horses are competing. The betting works as follows: If you bet one dollar on

horse k, then you get α

> 0 dollars if it comes in ﬁrst and 0 dollars otherwise.

Formulate a linear program to determine how much of a total of B dollars should

168 EQUIVALENT FORMULATIONS

Separation of

Region B Milk

Raw Milk

15% butterfat

Milk

43% butterfat

Milk

5% butterfat

Figure 6-7: Separation of Region B Milk

Minimum required

percentage of butterfat

Maximum volume

demanded in gallons

Selling price in

cents per gallon

Cream 40 250 150

Milk 20 2000 70

Table 6-2: Demand and Selling Price of Milk

you bet on each horse so as to maximize the minimum net gain, irrespective of

which horse comes in ﬁrst.

6.15 (a) Solve Problem 6.14 for N =2,α

=1,α

= 2, and B =1.

(b) Observe that the bets are inversely proportional to α

and α

. Prove that,

in general, the optimal solution is to bet inversely proportional to the return

onabetα

. Hint: Show that the bets x

, for j =1,...,N, must be basic

variables in an optimal solution and that they price out as optimal.

6.16 Suppose an experiment results in the data points shown in Table 6-3. It is

hypothesized that the relation is a cubic of the form

y = x

+ x

t + x

+ x

Find the parameters x

, x

that give the best ﬁt to the data. Solve

the problem using each of the three models described in this chapter. (Note:

For the least squares problem, simply set up and solve the normal equations

Ax = A

b.)

6.17 Davis & McKeown [1981]. Sigma Paper Company, Inc., is about to build a new

plant. The labor requirements to build the plant are 2,000 nonprofessionals and

t y

1 6

2 18

3 50

4 101

5 177

6 296

7 447

8 642

Table 6-3: Experimental Points for a Cubic

6.9 PROBLEMS 169

850 professionals. Because of labor market shortages in both categories, costs

for recruiting women and minorities are greater than for others. Speciﬁcally,

the cost for recruiting minorities (men or women) is $740 for nonprofessionals

and $1,560 for professionals. For recruiting nonprofessional women the cost

is $850 and for recruiting professional women the cost is $1,450. Otherwise

the recruiting costs for men average $570 for each nonprofessional position and

$1,290 for each professional position. The company has budgeted $2.4 million

for recruiting purposes, and the management has established the following goals

in order of priority.

Goal 1: At least 45% of the new labor force should be women.

Goal 2: Minorities should constitute at least 40% of the labor force. Fur-

thermore, a minority woman is counted both as a minority and

as a woman employee.

Goal 3: The cost of recruiting should be minimized.

Goal 4: The recruiting cost should be limited to $300,000.

(a) Use the goal programming technique to formulate a linear programming

model for this problem.

(b) Solve the problem using the software provided with the book.

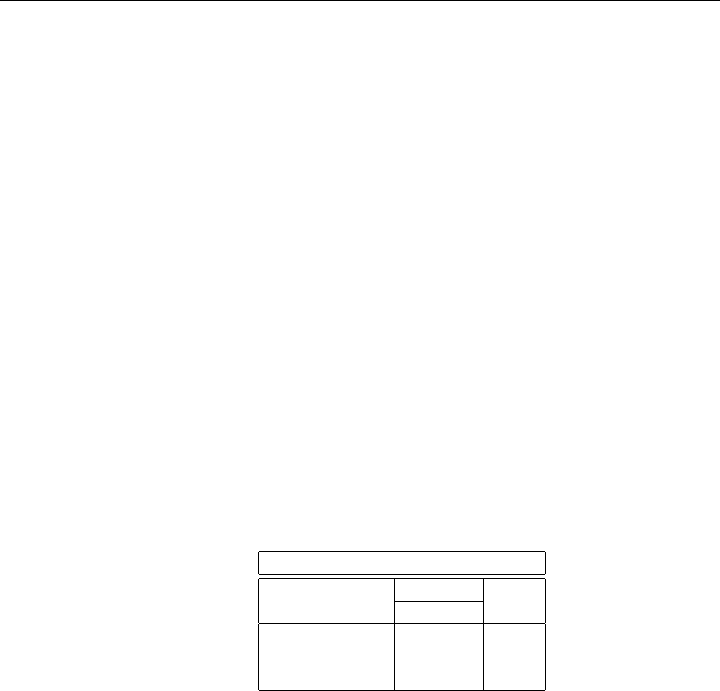
6.18 Adapted from Hillier & Lieberman [1995]. Consider a preemptive goal program-

ming problem with three priority levels, one goal for each priority level, and just

two activities to contribute towards these goals as shown in the table below:

Unit Contribution

Activity

Priority Level abGoal

One 12≤ 20

Two 11=15

Three 21≥ 40

(a) Use the goal programming technique to formulate a linear programming

model for this problem.

(b) Solve the problem using the software provided with the book.

ically by focusing on just the two decision variables. Clearly explain the

logic used.

(d) Use the sequential programming technique to solve this problem with the

software provided with the book. After using the goal programming tech-

nique to formulate the linear programming model at each stage, solve the

model graphically by focusing on just the two decision variables. Identify

all optimal solutions obtained for each stage.

6.19 Use the weighted goal programming method to solve Problem 6.18.

6.20 Estimate the failure rate x

of an item as a function of its age i. An experiment

is run with K new items put in use at time 0. Time is divided into unit intervals

and the number still working at the beginning of each interval is observed. If

we let f

be the number of items observed to be working at the start of time

interval i, then f

−f

i+1

are the number of items that failed during time interval i

170 EQUIVALENT FORMULATIONS

and a

=(f

− f

i+1

)/f

is the observed failure rate at the age of i time units.

Suppose that from engineering considerations we know that the failure rate in

a large population increases with age; this is the Increasing Failure Rate (IFR)

property. The actual failure rates in the experiment with only K items may not

be increasing due to random ﬂuctuations in the observations. The solution x

to the problem is required to satisfy the IFR property and at the same time be

one that is closest to the observed failure rates a in the sense of minimizing the

maximum absolute values of the diﬀerence. Formulate this problem.

6.21 Ubhaya [1974a, 1974b] in Murty [1983]. Let w =(w

,... ,w

)

> 0, a

vector of positive weights, be given. For each vector y ∈

, deﬁne the function

L(y)by

L(y) = max {w

| : i =1,...,n}.

Given a vector a ∈

, formulate a linear program to ﬁnd a vector x ∈

Minimize L(a − x)

subject to x

− x

i+1

≤ 0,i=1,...,n− 1.

(a) Show that this is a generalization of Problem 6.20, where we have attached

weights w

to the deviations.

(b) How does the formulation change if, in addition, each x

is required to be

nonnegative, and also less than or equal to one?

, and a =(0.20, 0.45, 0.35)

6.22 Solve the calculus problem

Minimize x

+ x

+2x

+4x

+8x

= z

subject to x

+ x

by using linear programming software and piecewise continuous linear approx-

imations to the quadratic functions (with upper and lower bounds on the vari-

ables introduced to make the approximations). What properties of the approx-

imates ensures the convexity of the approximations.

6.23 Consider the following problem, which has a convex objective function and linear

inequality constraints

Minimize x

+2x

= z

subject to 4x

+5x

≤ 20

+ x

≥ 2

Solve the problem using piecewise continuous linear approximations to the con-

vex function. Use 4, 8, and 12 pieces. Compare the results under the diﬀerent

approximations.

CHAPTER 7

PRICE MECHANISM AND

SENSITIVITY ANALYSIS

The term sensitivity analysis, sometimes called post-optimality analysis, refers to

an analysis of the eﬀect on the optimal solution of changes in the input-output

coeﬃcients, cost coeﬃcients, and constant terms. Such analysis can often be more

important in practice than ﬁnding the optimal solution. It is a very important part

of solving linear programs in practice. Most practical problems have input data

whose values are not known with certainty. For example, the costs of raw materials

may change after the model is solved, or the costs used in the model may only be

a guess as to what they will be in the future; the right-hand-side constraints may

have to be changed because more or less of the resources are available in the market

than previously estimated or were earlier authorized by management to buy; or

the coeﬃcients may have to be changed because product speciﬁcations have been

changed.

In addition to the optimal tableau giving us the point of most proﬁtable op-

eration, it is possible to obtain from it a wealth of information concerning a wide

range of operations in the neighborhood of this optimum by performing a sensitivity

analysis. As noted, in many applications, the information obtained is often more

valuable than the speciﬁcation of the optimum solution itself.

Sensitivity analysis is important for several reasons:

1. Stability (robustness) of the optimum solution under changes of parameters

may be highly desirable. For example, using the old optimum solution point;

a slight variation of a parameter in one direction may result in a large unfavor-

able diﬀerence in the objective function relative to the new minimum, while

a large variation in the parameter in another direction may result in only a

small diﬀerence. In an industrial situation where there are certain inherent

171