Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

3.2 Convergence Tests for Series 73

PROOF. Let s

k=1

(−1)

. Intuitively, (s

) behaves as in Figure 3.2.

FIGURE 3.2. Behaviour of partial sums.

Making this formal, we claim that

(1) s

≥ s

···,

(2) s

≤ s

···, and

(3) s

2m−1

≤ s

for all m, n ≥ 1.

To prove (1), notice that s

− s

2n−2

= a

− a

2n−1

≤ 0 since a

≤ a

2n−1

For (2), s

2n+1

− s

2n−1

= a

− a

2n+1

≥ 0.

The inequalities in (3) follow simply from (1) and (2). For any positive in-

teger N, s

= s

2N−1

+ a

≥ s

2N−1

. If m and n are integers, then for

N = max{m, n}, we have

2m−1

≤ s

2N−1

≤ s

The ﬁrst inequality follows from (1), we have just proved the second, and the third

follows from (2).

Since the sequence (s

, s

, . . .) is bounded below by s

, it converges to some

number L by Theorem 2.5.4. Similarly, since (s

, s

, . . .) is bounded above by s

it converges to some number M .

All that remains is to show L = M. To do this, we use the properties of limits,

L − M = lim

n→∞

− lim

n→∞

2n−1

= lim

n→∞

− s

2n−1

= lim

n→∞

= 0.

Note that the proof gives upper and lower bounds on

∞

n=1

(−1)

, namely the

even and odd partial sums, respectively. Precisely, we have the following statement.

3.2.7. COROLLARY. Suppose that (a

)

∞

n=1

is a monotone decreasing sequence

≥ a

≥ ··· ≥ 0 and that lim

n→∞

= 0. Then the difference between the

sum of the alternating series

∞

n=1

(−1)

and the Nth partial sum is at most |a

3.2.8. EXAMPLE. Consider the alternating harmonic series

∞

n=1

(−1)

n−1

= 1 −

−

+ . . . .

Since this series is alternating and

is monotone decreasing to 0, the series must

converge. Compare this with the harmonic series, which has the same terms without

the sign changes.

74 Series

It is possible to sum this series in several ways. All rely on calculus in some

way. Notice that

k=1

(−1)

k−1

= 1 −

+ ··· +

2n − 1

−

1 +

+ ··· +

2n − 1

− 2

+ ··· +

k=1

− 2

k=1

−

k=1

n + k

We have to recognize this as a Riemann sum approximating an integral. Indeed,

consider the integral

dx. Partition the interval [1, 2] into n equal pieces. Then

1 2

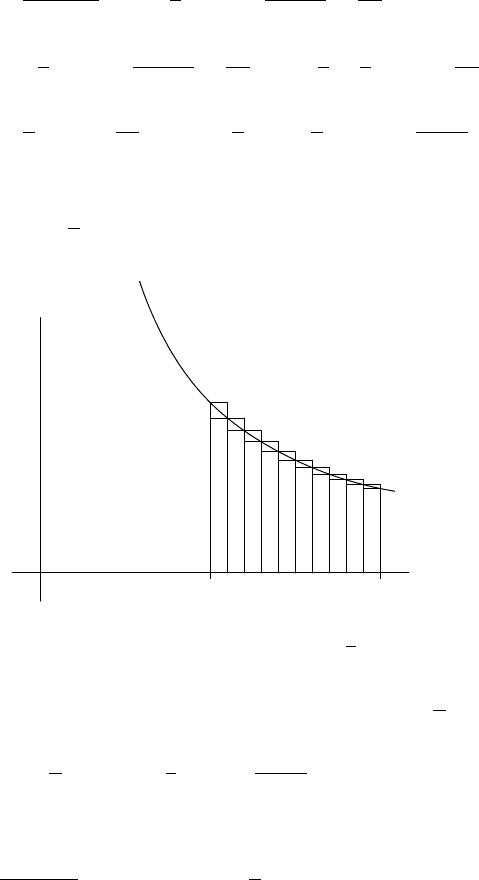
FIGURE 3.3. Riemann sum for

dx.

from Figure 3.3, we see that the Riemann (lower) sum for f (x) =

k=1

1 +

k=1

n + k

= s

From the calculus, we obtain

∞

n=1

(−1)

n−1

= lim

n→∞

dx = log x

= log 2.

Exercises for Section 3.2

A. Prove Theorem 3.2.2.

B. Show that if (|a

∞

n=1

is summable, then so is (a

)

∞

n=1

3.2 Convergence Tests for Series 75

C. Euler proposed that 1 − 2 + 4 −8 + ··· =

∞

n=0

(−2)

1 − (−2)

What is wrong with this argument?

D. Let (a

)

∞

n=1

be a monotone decreasing sequence of positive real numbers. Show that

the series

∞

n=1

converges if and only if the series

∞

k=0

converges.

E. Apply the previous exercise to the series

∞

n=1

for p > 0. For which values of p does

this converge?

F. Let

∞

n=1

be a convergent series of positive terms.

(a) Show that

∞

n=1

√

converges for p > 1/2. HINT: Schwarz inequality

(b) Find an example for which the series

∞

n=1

diverges.

G. If

∞

k=1

and

∞

k=1

both converge, then prove that

∞

k=1

converges.

H. (THE LIMIT COMPARISON TEST) Show that if

∞

n=1

and

∞

n=1

are series with

≥ 0 such that limsup

n→∞

< ∞ and

∞

n=1

< ∞, then the series

∞

n=1

converges.

I. (THE RATIO TEST) Suppose that (a

)

∞

n=1

is a sequence of positive terms. Show that if

limsup

n→∞

n+1

< 1, then

∞

n=1

converges. Conversely, show that if liminf

n→∞

n+1

> 1,

then

∞

n=1

diverges.

HINT: Imitate the proof of the Root Test (i.e., ﬁnd a suitable r and integer N > 0 and

compare a

with a

n−N

for all n ≥ N).

J. (a) Find a convergent series

∞

n=1

, with positive entries, so that lim

n→∞

n+1

= 1.

(b) Find a divergent series with the same property.

K. Construct a convergent series of positive terms with limsup

n→∞

n+1

= ∞.

L. Prove that for a sequence of positive terms (a

), if there is N with a

n+1

≥ 1 for

all n ≥ N, then the series

∞

n=1

diverges. Show that this result implies one direction

of the Ratio Test (Exercise I).

M. (a) Find a convergent series

∞

n=1

, with positive entries, so that lim

n→∞

√

= 1.

(b) Find a divergent series with the same property.

N. If a

≥ 0 for all n, prove that

∞

n=1

converges if and only if

∞

n=1

1 + a

converges.

76 Series

O. (THE INTEGRAL TEST) Let f(x) be a positive monotone decreasing function on

[1, ∞). Show that the sequence

f(n)

is summable if and only if

∞

f(x) dx < ∞.

HINT: Show that

k+1

n=2

f(n) <

k+1

f(x) dx <

n=1

f(n).

P. Apply the previous exercise to the series

∞

n=2

n(logn)

for p > 0.

Q. Find two convergent series

∞

k=1

and

∞

k=1

so that

∞

k=1

diverges.

R. Let

n≥1

be a divergent series of positive terms. Set s

i=1

(a) Prove that

n≥1

converges for p > 1.

HINT: Rewrite the sum as

n≥1

−p

− s

−p

n+1

n≥1

−1/p

− t

n+1

Bound the latter sum by an integral.

(b) Prove that

n≥1

diverges.

HINT: First consider a

≥ s

n−1

. Then group terms to achieve this.

S. Determine if the following series converge or diverge.

(a)

∞

n=2

+ 1

(b)

∞

n=1

(c)

∞

n=2

(−1)

logn

(d)

∞

n=1

√

n + 1 −

√

n (e)

∞

n=1

−n

(f)

∞

n=1

sin(nπ/4)

(g)

∞

n=1

(−1)

sin(1/n) (h)

∞

n=1

√

+ 4

(i)

∞

n=1

(

√

n − 1)

(j)

∞

n=2

√

n + 1 −

√

(k)

∞

n=2

(−1)

√

n log n

(l)

∞

n=2

(−1)

√

(m)

∞

n=2

(logn)

(n)

∞

n=1

(o)

∞

n=1

(−1)

arctan(n)

(p)

∞

n=2

(−1)

√

n + (−1)

(q)

∞

n=1

(−1)

1/n

− 1) (r)

∞

n=1

(−1)

(n + 1)!

(s)

∞

n=1

1 + n

(t)

∞

n=1

log(e

+ e

−n

)

(u)

∞

n=1

sin(πn/3)

(v)

∞

n=1

(w)

∞

n=2

(logn)

(x)

∞

n=2

n log n

(y)

∞

n=1

sin

(z)

∞

n=1

1+1/n

3.3 The Number e 77

3.3. The Number e

Recall from calculus the formula

e = 1 + 1 +

+ ··· =

∞

k=0

≈ 2.7182818285 . . .

If you don’t recall this, you can review the section on Taylor series in your calculus

book or study Example 10.1.4 later in this book. With a

= 1/k!, we obtain

lim

k→∞

k+1

= lim

k→∞

k + 1

= 0.

Thus this series converges by the Ratio Test. The limit is called e.

There are other ways to compute e. We give one such well-known formula and

verify that it has the same limit.

3.3.1. PROPOSITION. Consider the sequences

1 +

and c

1 +

n+1

These sequences are monotone increasing and decreasing, respectively, and

lim

n→∞

1 +

= lim

n→∞

1 +

n+1

= e.

PROOF. We need the inequality:

(1 + x)

> (1 + nx) for x > −1 and n ≥ 1.

To see this, let f(t) = (1 + t)

− (1 + nt). Notice that f(0) = 0 and

(t) = n

(1 + t)

n−1

− 1

for t > −1.

Thus f is decreasing on (−1, 0] and increasing on [0, ∞), and so takes its minimum

value at 0.

As c

1 +

, we have b

< c

for n ≥ 1. Now compute

n+1

1 +

n+1

1 +

n+1

+ 2n

+ 2n + 1

n+1

1 −

(n + 1)

n+1

> 1 −

n + 1

(n + 1)

n + 1

Therefore,

n+1

n + 1

= b

Similarly, inverting the preceding identity,

n+1

1 +

+ 2n

n+1

> 1 +

n + 1

+ 2n

n + 2

n + 1

whence c

n+1

n + 2

n + 1

n+1

< c

78 Series

It follows that (b

)

∞

n=1

is a monotone increasing sequence bounded above by

. Thus it converges to some limit L by Theorem 2.5.4. Similarly, (c

)

∞

n=1

is a

monotone decreasing sequence bounded below by b

, and

lim

n→∞

= lim

n→∞

1 +

= L.

Next we use the Binomial Theorem to estimate the terms b

1 +

k=0

(n − 1)

···

(n − k + 1)

k=0

1 −

´³

1 −

···

1 −

k − 1

It follows that b

< s

k=0

, and therefore

L = lim

n→∞

≤ lim

n→∞

= e.

On the other hand, this also provides the lower bound. If p is a ﬁxed integer, then

k=0

1 −

´³

1 −

···

1 −

k − 1

1 −

´³

1 −

···

1 −

p − 1

Thus

L = lim

n→∞

≥ lim

n→∞

1 −

´³

1 −

···

1 −

p − 1

= s

for all p ≥ 1. So

L ≥ lim

p→∞

= e.

We obtain

lim

n→∞

1 +

= lim

n→∞

1 +

n+1

= e.

Inﬁnite series have unexpected uses. We use the series for e to prove that it is

not a rational number.

3.3.2. THEOREM. e is irrational.

PROOF. Suppose that e is rational and can be written as e = p/q in lowest terms,

where p and q are positive integers. We look for a contradiction. Do the following

calculation:

(q − 1)!p = q!

= q!e = q!

∞

k=0

∞

k=q+1

3.3 The Number e 79

Rearranging, we get

∞

k=q+1

= (q − 1)!p −

k=1

Since both terms on the right-hand are integers, the left-hand side must also be an

integer. However, using the properties of limits, we have

0 <

∞

k=q+1

q + 1

(q + 1)(q + 2)

(q + 1)(q + 2)(q + 3)

+ ···

q + 1

(q + 1)

+ ···

n≥1

q + 1

1/(q + 1)

1 − 1/(q + 1)

≤ 1.

Therefore, 0 <

∞

k=q+1

< 1, contradicting the conclusion that this summation is

an integer. ¥

Exercises for Section 3.3

A. (a) Show that

∞

k=0

converges for each x ∈ R. The limit is called e

(b) Show that lim

n→∞

1 +

= e

. HINT: Compare with the series in part (a).

B. Compute the sum of the series

∞

n=1

+ 2

+ ··· + n

HINT: Use induction to show that 1

+ 2

+ ··· + n

= n(n + 1)(2n + 1)/6.

Then express this in the form An(n − 1)(n − 2) + Bn(n − 1) + Cn + D.

C. Compute the sum of the series

∞

n=0

(2n + 1)!

HINT: Express this as the difference of two known series.

D. Evaluate lim

n→∞

1 +

n+1

−(n+1)

E. Decide whether

∞

n=1

converges.

F. Show that the Root Test implies the Ratio Test by proving that if lim

n→∞

n+1

= r, then

lim

n→∞

)

1/n

= r.

G. Combine the two previous exercises to compute lim

n→∞

√

H. Decide if

∞

n=1

(logn)

log n

converges. HINT: Show that (logn)

log n

= n

log logn

80 Series

I. If a is a real number, consider the limit lim

n→∞

sin(n!πa).

(a) If a is rational, ﬁnd the limit.

(b) Show that n!

∞

k=n+1

n→∞

sin((2n)!πa).

J. Show that

√

2 + e is irrational.

3.4. Absolute and Conditional Convergence

In this section, we further investigate convergence properties of series. The

Alternating Series Test shows that badly behaved series such as the harmonic series

become more tractable when appropriate signs for the terms keep the partial close

together. However, the following variant on Example 3.2.8 shows that considerable

care must be taken when adding this type of series.

3.4.1. EXAMPLE. Consider the series

1 −

−

+ . . . ,

where a

3n−2

2n−1

, a

3n−1

= −

4n−2

and a

= −

. This has exactly the same

terms as the alternating harmonic series except that the negative terms are coming

twice as fast as the positive ones.

First let’s convince ourselves that this series converges. Notice that

3n−2

+ a

3n−1

+ a

2n − 1

−

4n − 2

−

4n − 2n − (2n − 1)

4n(2n − 1)

Therefore, s

k=1

4k(2k − 1)

. The terms of this series are dominated by the

series

∞

k=1

. This latter series converges by the Integral Test (see Exercise 3.2.O)

because

∞

dx = −

∞

< ∞.

Therefore, lim

n→∞

∞

k=1

4k(2k − 1)

converges by the Comparison Test (3.2.3).

However, |s

− s

3n±1

| <

. With a little bit of work (see Exercise 2.6.G), we

can show that the limit exists, using

lim

n→∞

3n−1

= lim

n→∞

3n+1

= lim

n→∞

= lim

n→∞

The proof of the Integral Test yields the estimate

∞

n=1

∞

dx =

3.4 Absolute and Conditional Convergence 81

Hence our limit is also less than

. However, the alternating harmonic series has the

limit log2 ≈ 0.6931471806. So these two series have different sums even though

they have the same terms. We can actually sum this series exactly because

4k(2k − 1)

2k − 1

−

Therefore,

k=1

(−1)

n+1

By Example 3.2.8, we conclude that the series converges to

log2.

3.4.2. DEFINITION. A series

∞

n=1

is called absolutely convergent if the

series

∞

n=1

| converges. A series that converges but is not absolutely convergent

is called conditionally convergent.

Example 3.2.8 shows that a convergent series need not be absolutely conver-

gent. The next simple fact is that absolute convergence is a stronger notion than

convergence. The proof is left to Exercise 3.2.B, which is an easy application of

the Comparison Test to the series

∞

n=1

and

∞

n=1

3.4.3. PROPOSITION. An absolutely convergent series is convergent.

Consider the question of what happens when the terms of a series are permuted.

3.4.4. DEFINITION. A rearrangement of a series

∞

n=1

is another series with

the same terms in a different order. This can be described by a permutation π of the

natural numbers N determining the series

∞

n=1

π(n)

The situation for absolutely convergent series is good.

3.4.5. THEOREM. For an absolutely convergent series, every rearrangement

converges to the same limit.

PROOF. Let

∞

n=1

be an absolutely convergent series that converges to L. Suppose

that π is a permutation of N and that ε > 0 is given. Then there is an integer N

such that

∞

k=N +1

| < ε/2.

82 Series

Since the rearrangement contains exactly the same terms in a different order,

the ﬁrst N terms a

, . . . , a

eventually occur in the rearranged series. Thus there is

an integer M so that all of these terms occur in the ﬁrst M terms of the rearrange-

ment. Hence for m ≥ M,

k=1

π(k)

− L

≤

k=1

π(k)

−

k=1

− L

≤ 2

∞

k=N +1

| < ε.

Therefore,

∞

k=1

π(k)

= L. ¥

3.4.6. EXAMPLE. Consider the series

∞

n=1

(−1)

n+1

. This converges by the

Alternating Series Test. In fact, it is absolutely convergent since the series

∞

n=1

converges by the Integral Test (verify). Hence we may manipulate the terms freely.

Therefore,

∞

n=1

(−1)

n+1

∞

n=1

− 2

∞

n=1

(2n)

∞

n=1

Using techniques from Fourier series (see Chapter 14), we will be able to show

that

∞

n=1

1/n

= π

/90. From this, it follows that the preceding summation equals

7π

/720.

On the other hand, the worst possible scenario holds for the rearrangements of

conditionally convergent series. First, we need the following dichotomy.

3.4.7. LEMMA. Let

∞

n=1

be a convergent series. Denote the positive terms as

, b

, . . . and the other terms as c

, c

, . . . .

(1) If

∞

n=1

is absolutely convergent, then so are both

∞

n=1

and

∞

n=1

and

∞

n=1

∞

n=1

−

∞

n=1

(2) If

∞

n=1

is conditionally convergent, then

∞

n=1

and

∞

n=1

|both diverge.

PROOF. If the series (a

) is absolutely convergent, consider the new sequence

given by x

= max{a

, 0}. This is just the sequence (b

) in order with zeros in