Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

2.8 Appendix: Cardinality 63

There are inﬁnite sets that are not countable.

2.8.7. THEOREM. The set R of real numbers is uncountable.

PROOF. The proof uses a diagonalization argument due to Cantor. Suppose to

the contrary that R is countable. Then all real numbers may be written as a list

, x

, . . . . Express each x

as an inﬁnite decimal, which we write as x

. . . , where x

is any integer and x

is an integer from 0 to 9 for each

k ≥ 1. Our goal is to write down another real number that does not appear in this

(supposedly exhaustive) list. Let a

= 0 and deﬁne a

= 7 if x

∈ {0, 1, 2, 3, 4}

and a

= 2 if x

∈ {5, 6, 7, 8, 9}. Deﬁne a real number a = a

. . . .

Since a is a real number, it must appear somewhere in this list, say a = x

However, the kth decimal place a

of a and x

of x

differ by at least 3. This

cannot be accounted for by the fact that certain real numbers have two decimal

expansions, one ending in zeros and the other ending in nines because this changes

any digit by no more than 1 (counting 9 and 0 as being within 1). So a 6= x

, and

hence a does not occur in this list. It follows that there is no list containing all real

numbers, and thus R is uncountable. ¥

We conclude with the result promised in the start of this section.

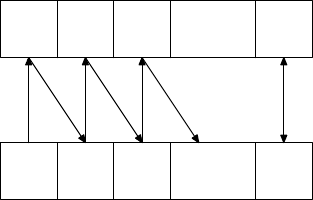
2.8.8. SCHROEDER–BERNSTEIN THEOREM.

If A and B are sets with |A| ≤ |B| and |B| ≤ |A|, then |A| = |B|.

PROOF. The proof is surprisingly simple. Since |A| ≤ |B|, there is an injection f

mapping A into B. Likewise, as |B| ≤ |A|, there is an injection g mapping B into

A. Let B

= B \ f (A). Recursively deﬁne A

= g(B

) and B

i+1

= f(A

) for

i ≥ 1. Deﬁne A

= A \

i≥1

and B

= B \

i≥1

. We will show that the

actions of f and g ﬁt the scheme of Figure 2.6.

···

g g g

f f

FIGURE 2.6. Schematic of action of f and g on A and B.

First we show that the B

’s are disjoint. Clearly each B

for i ≥ 2 is in the range

of f and hence does not intersect B

. Suppose that 1 < i < j. Then (f g)

i−1

is an

injection of B into itself that carries B

onto B

k+i−1

for every k ≥ 1. In particular,

is mapped onto B

and B

j−i+1

is mapped onto B

. Since B

∩ B

j−i+1

= ∅

and (fg)

i−1

is one-to-one, it follows that B

∩ B

= ∅.

64 The Real Numbers

By construction, g

−1

is a bijection of each A

onto B

for i ≥ 1. We claim that

f maps A

onto B

. Observe that f maps A

onto B

i+1

for each i ≥ 1. Thus the

remainder of A, namely A

, is mapped onto the remainder of the image. Thus

f(A

) = f (A) \

[

i≥1

f(A

) = (B \ B

) \

[

i≥1

i+1

= B \

[

i≥1

= B

This means that the function

h(a) =

(

−1

(a) if a ∈

i≥1

f(a) if a ∈ A

is a bijection between A and B. So |A| = |B|. ¥

The whole subject of cardinality is wrapped up in the subtleties of set theory.

The commonly used axioms of set theory include the Axiom of Choice, which has

the simple sounding statement that given any collection of nonempty sets, one can

select an element from each of them. This has many signiﬁcant ramiﬁcations that

are beyond the scope of this book. One of these is that if A and B are any sets, then

either |A| ≤ |B| or |B| ≤ |A|.

Another aspect of set theory that arises in this context is that sets must be built

up from smaller sets only in certain allowable ways. This prevents the universe of

all sets from being a set itself. The reason behind this is a famous contradiction,

known as Russell’s Paradox, to a more casually deﬁned theory of sets.

Russell’s argument is like Cantor’s diagonalization argument. Let X be the

set consisting of all sets A that do not contain themselves as an element. Intuition

suggests that no set contains itself. However, the set of all sets (were it a set) would

have to contain itself, and thus is not an element of X. The question is, Does X

contain itself? If X does not contain itself, then by deﬁnition, it does belongs to X.

Conversely, if X is an element of X, then by deﬁnition it would not be a member.

So neither possibility is logical.

The solution was proposed by Zermelo in 1908 and reﬁned by various other

mathematicians, culminating in a ﬁnished version by Fraenkel in 1922. The stan-

dard axioms of set theory used by most mathematicians today are called ZFC, for

Zermelo–Fraenkel set theory with the Axiom of Choice.

A curious question in the fundamentals of set theory was raised by Cantor.

If A is an uncountable subset of R, is |A| = |R|? The continuum hypothesis

asserts that the answer is yes. There is also a generalized continuum hypothesis

that makes a parallel assertion about all larger cardinal numbers, not just |R|. The

Austrian mathematician G

odel established several deep results about the founda-

tions of mathematics. One of these was that, if there is an inconsistency of ZFC

together with the generalized continuum hypothesis, then there is an inconsistency

in the Zermelo–Fraenkel axioms themselves. This means that there is no additional

danger of an inconsistency in assuming the Axiom of Choice or the generalized

continuum hypothesis. In 1965, Cohen showed that the generalized continuum

hypothesis does not follow from ZFC, so we are also free to not assume the gener-

alized continuum hypothesis, if we so choose.

2.8 Appendix: Cardinality 65

Any further discussion of these issues leads far away from analysis and the

purpose of this book. We refer the interested reader to [1] as a starting point for the

study of set theory.

Exercises for Section 2.8

A. Prove that the set Z

, consisting of all n-tuples a = (a

, a

, . . . , a

), where a

∈ Z, is

countable.

B. Do (0, 1) and [0, 1] have the same cardinality as R? Do not use the Schroeder–

Bernstein Theorem.

C. Show that if |A| ≤ |B| and |B| ≤ |C|, then |A| ≤ |C|.

D. Show that the relation of equal cardinality |A| = |B| is an equivalence relation.

E. Show that |R

| = |R|.

F. Prove that the set of all inﬁnite sequences of integers is uncountable.

HINT: Modify the diagonalization argument.

G. A real number α is called an algebraic number if there is a polynomial with integer

coefﬁcients with α as a root. Prove that the set of all algebraic numbers is countable.

HINT: First count the set of all polynomials with integer coefﬁcients.

H. A real number that is not algebraic is called a transcendental number. Prove that the

set of transcendental numbers has the same cardinality as R.

I. Show that the set of all ﬁnite subsets of N is countable.

J. Prove Cantor’s Theorem: that for any set X, the power set P(X) of all subsets of X

satisﬁes |X| 6= |P (X)|.

HINT: If f is an injection from X into P (X), consider A = {x ∈ X : x 6∈ f(x)}.

K. If A is an inﬁnite set, show that A has a countable subset.

HINT: Use recursion to choose a sequence a

of distinct points in A.

L. Show that A is inﬁnite if and only if there is a proper subset B of A such that |B| = |A|.

HINT: Use the previous exercise and let B = A \ {a

CHAPTER 3

Series

3.1. Convergent Series

We turn now to the problem of adding up an inﬁnite series of numbers. As

we shall quickly see, this is really no different from dealing with the sequence of

partial sums of the series. However, there are tests for convergence that are more

conveniently expressed for series than for sequences.

3.1.1. DEFINITION. If (a

)

∞

n=1

is a sequence of numbers, the inﬁnite series

with terms a

is the formal expression

∞

n=1

. This series converges or, equiva-

lently, the sequence is summable if the sequence of partial sums (s

)

∞

n=1

deﬁned

by s

k=1

converges. If L = lim

n→∞

, then L is the sum of the series, and we

write L =

∞

n=1

. If the series does not converge, then it is said to diverge.

It is worth pointing out that the convergence of the series

∞

n=1

and of the

sequence (a

)

∞

n=1

are two very different questions. We will work out the exact

relation between these concepts in this chapter.

It can be fairly difﬁcult or even virtually impossible to ﬁnd the sum of a series.

However, it is not nearly as hard to determine whether or not a series converges.

We devote this chapter to examples of series and to tests for convergence of series.

While these tests may be familiar to you from calculus, the proofs may not be. And

of course, you should learn both how to use these tests and how to prove that the

tests are correct.

3.1.2. EXAMPLE. First consider

∞

k=1

, which is known as the harmonic series.

We will show that this series diverges. The idea is to group the terms cleverly.

3.1 Convergent Series 67

Suppose that n satisﬁes 2

≤ n < 2

k+1

. Then

= 1 +

+ ··· +

> 1 +

+ (

) + ··· + (

k−1

+ 1

+ ··· +

)

≥ 1 +

+ 2

+ ··· + 2

k−1

= 1 +

Thus lim

n→∞

= +∞.

There is another way to estimate the terms s

that gives a more precise idea of

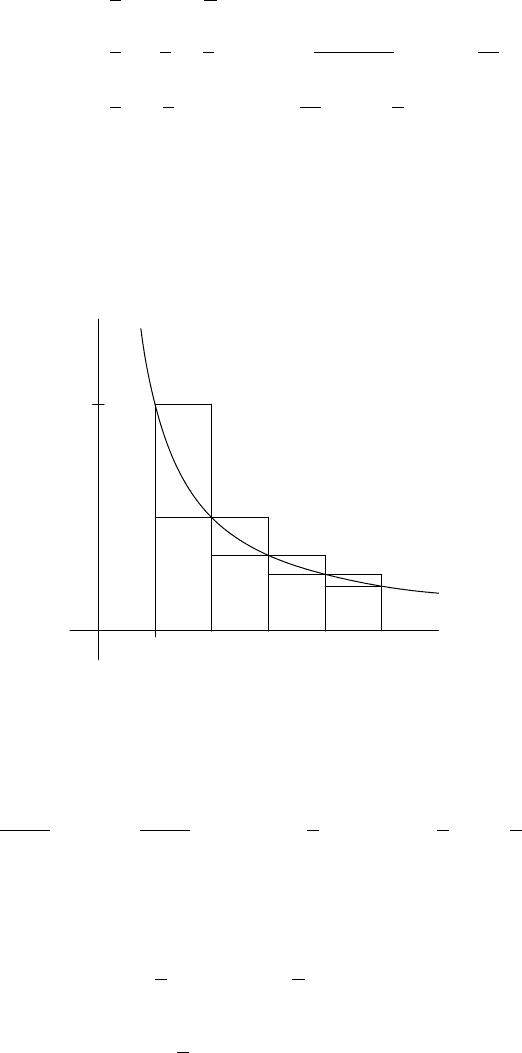
the rate of divergence of the harmonic series. Consider the graph of y = 1/x, as

given in Figure 3.1.

1 2 3 4 5

FIGURE 3.1. The graph of 1/x with bounding rectangles.

It is clear that

k + 1

k+1

k + 1

dx <

k+1

dx <

k+1

dx =

Notice that s

is the upper Riemann sum estimate for the integral of 1/x from 1 to

n + 1 using the integer partition.

k=1

k+1

n+1

dx = log x

n+1

= log(n + 1).

68 Series

Similarly, s

− 1 is the lower Riemann sum estimate for the integral of 1/x

from 1 to n using the integer partition.

− 1 =

k=2

k−1

dx = log x

= log(n)

Therefore,

log(n + 1) < s

< 1 + log(n) for all n ≥ 1.

Hence s

diverges to inﬁnity roughly at the same rate as the log function.

3.1.3. EXAMPLE. On the other hand, consider

∞

n=1

n(n + 3)

. First observe that

n(n + 3)

−

n + 3

and so we have an example of a telescoping sum (so named because of the conve-

nient cancellation in the following sum):

+ ··· +

n(n + 3)

1 −

−

+ ··· +

−

n + 3

1 +

+ ··· +

−

+ ··· +

n + 3

= 1 +

−

n + 1

−

n + 2

−

n + 3

Thus,

∞

n=1

n(n + 3)

= lim

n→∞

1 + 1/2 + 1/3

The harmonic series shows that a series

∞

n=1

can diverge even if the a

go to

zero. However, if a series

∞

n=1

does converge, then lim

n→∞

must be zero. That

is, lim

n→∞

= 0 is necessary for

∞

n=1

to converge, but it is not sufﬁcient to make

∞

n=1

converge.

3.1.4. THEOREM. If the series

∞

n=1

is convergent, then lim

n→∞

= 0.

3.1 Convergent Series 69

PROOF. If (s

)

∞

n=1

is the sequence of partial sums, then a

= s

−s

n−1

for n ≥ 2.

Using the properties of limits, we have lim

n→∞

= lim

n→∞

n−1

, and thus

lim

n→∞

= lim

n→∞

− s

n−1

= lim

n→∞

− lim

n→∞

n−1

= 0.

The rigorous ε–N deﬁnition of convergence and the Cauchy criterion have a

nice form for series.

3.1.5. CAUCHY CRITERION FOR SERIES.

The following are equivalent for a series

∞

n=1

(1) The series converges.

(2) For every ε > 0, there is an N ∈ N so that

∞

k=n+1

< ε for all n ≥ N.

(3) For every ε > 0, there is an N ∈ N so that

k=n+1

< ε if n, m ≥ N.

PROOF. Let s

be the sequence of partial sums of the series. If the series converges

to a limit L, then for every ε > 0 there is an integer N such that

|L − s

| < ε for all n ≥ N.

Moreover,

L − s

= lim

m→∞

− s

= lim

m→∞

k=n+1

∞

k=n+1

This shows that (1) implies (2).

If (2) holds, then the previous paragraph shows that there is an integer N so

that (for ε/2)

|L − s

| <

for all n ≥ N.

Thus

k=n+1

= |s

− s

| ≤ |s

− L| + |L − s

| <

= ε.

So (3) holds.

Finally, if (3) holds, this says that (s

) is a Cauchy sequence, and therefore it

converges by the completeness of the real numbers. ¥

70 Series

Exercises for Section 3.1

A. Sum the series

∞

n=1

n(n + 2)

B. Sum the series

∞

n=1

n(n + 1)(n + 3)(n + 4)

HINT: Show that

n(n + 1)(n + 3)(n + 4)

−

n + 1

n + 3

−

n + 4

C. Prove that if

∞

k=1

is a convergent series of nonnegative numbers and p > 1, then

∞

k=1

converges.

D. Let (a

)

∞

n=1

be a sequence such that lim

n→∞

| = 0. Prove that there is a subsequence

so that

∞

k=1

converges.

E. Compute

∞

n=1

(n + 1)

√

n + n

√

n + 1

HINT: Multiply the nth term by 1 =

√

n + 1 −

√

n + 1 −

√

and simplify.

F. Let |a| < 1 and set S

k=0

and T

k=0

(k + 1)a

(a) Show that S

k=0

(k + 1)a

k=1

(n + 1 −k)a

n+k

(b) Hence show that |T

− S

| ≤

n(n+1)

|a|

n+1

n→∞

lim

n→∞

. Hence obtain a formula for this sum.

(d) Evaluate

∞

k=0

n + 1

G. Let x

= 1 and x

n+1

= x

+ 1/x

(a) Find lim

n→∞

(b) Let y

= x

− 2n. Find a recursion formula for y

n+1

in terms of y

only.

is monotone increasing and y

< 2 + logn.

(d) Hence show that lim

n→∞

−

√

2n = 0.

3.2. Convergence Tests for Series

We start by considering inﬁnite series with positive terms. If each a

≥ 0, then

n+1

= s

n+1

≥ s

, so the sequence of partial sums is increasing. This fact and

the Monotone Convergence Theorem (Theorem 2.5.4) show that (s

) converges if

and only if it is bounded above. We have established the following proposition.

3.2 Convergence Tests for Series 71

3.2.1. PROPOSITION. If a

≥ 0 for k ≥ 1 and s

k=1

, then either

(1) (s

)

∞

n=1

is bounded above, in which case

∞

n=1

converges,

(2) (s

)

∞

n=1

is unbounded, in which case

∞

n=1

diverges.

A sequence

∞

n=0

is a geometric sequence with ratio r if a

n+1

= ra

for

all n ≥ 0 or, equivalently, a

= a

for all n ≥ 0. Finding the sum of a geometric

sequence is a standard result from the calculus, so we content ourselves with stating

the result and leave the proof as an exercise.

3.2.2. GEOMETRIC SERIES.

A geometric series converges if |r| < 1. Moreover,

∞

n=0

1 − r

Of course, if a 6= 0 and |r| ≥ 1, then the terms ar

do not converge to 0. In

this case, the geometric sequence

∞

n=0

is not summable.

Another possibly familiar test is the Comparison Test.

3.2.3. THE COMPARISON TEST.

Consider two sequences of real numbers (a

) and (b

) with |a

| ≤ b

for all

n ≥ 1. If (b

) is summable, then (a

) is summable and

∞

n=1

≤

∞

n=1

If (a

) is not summable, then (b

) is not summable.

PROOF. Let ε > 0 be given. Since (b

) is summable, Lemma 3.1.5 yields an

integer N so that

k=n+1

< ε for all N ≤ n ≤ m.

Therefore,

k=n+1

≤

k=n+1

| ≤

k=n+1

< ε.

Therefore, applying Lemma 3.1.5 again shows that

∞

n=1

converges.

Conversely, if (a

) is not summable, then neither is (b

), for the summability

of (b

) would imply that (a

) was also summable. This is the contrapositive of the

previous paragraph. ¥

The root test can decide the summability of sequences that are dominated by a

geometric sequence “at inﬁnity.”

72 Series

3.2.4. THE ROOT TEST.

Suppose that a

≥ 0 for all n and let ` = limsup

√

. If ` < 1, then

∞

n=1

converges, and if ` > 1, then

∞

n=1

diverges.

NOTE: If limsup

√

= 1, the series may or may not be converge (see Exer-

cise 3.2.M).

PROOF. Suppose that limsup

n→∞

√

= ` < 1. To show the series converges, we

need to show that the sequence of partial sums is bounded above. Pick a number r

with ` < r < 1 and let ε = r − `. Since ε > 0, we can ﬁnd an integer N > 0 so

that

1/n

< ` + ε = r for all n ≥ N.

Therefore, a

< r

for all n ≥ N .

Consider the sequence (b

)

∞

n=1

given by

= a

, 1 ≤ n < N b

= r

, n ≥ N.

This sequence is summable by Theorem 3.2.2.

∞

n=1

N−1

n=1

∞

n=N

N−1

n=1

1 − r

Since |a

| ≤ b

for n ≥ 1, the Comparison Test (3.2.3) shows that the sequence

)

∞

n=1

is also summable.

Conversely, if limsup

n→∞

√

= ` > 1, then let ε = ` −1. From the deﬁnition of

limsup, there is a subsequence n

< n

< . . . so that

1/n

> ` − ε = 1 for all k ≥ 1.

Therefore, the terms a

do not converge to 0 and thus the series diverges. ¥

3.2.5. DEFINITION. A sequence is alternating if it has the form ((−1)

) or

((−1)

n+1

), where a

≥ 0 for all n ≥ 1.

3.2.6. LEIBNIZ ALTERNATING SERIES TEST.

Suppose that (a

)

∞

n=1

is a monotone decreasing sequence a

≥ a

≥ ··· ≥ 0

and that lim

n→∞

= 0. Then the alternating series

∞

n=1

(−1)

converges.