Дементьев Ю.Н., Чернышев А.Ю., Чернышев И.А. Автоматизированный электропривод (учебное пособие)

Подождите немного. Документ загружается.

201

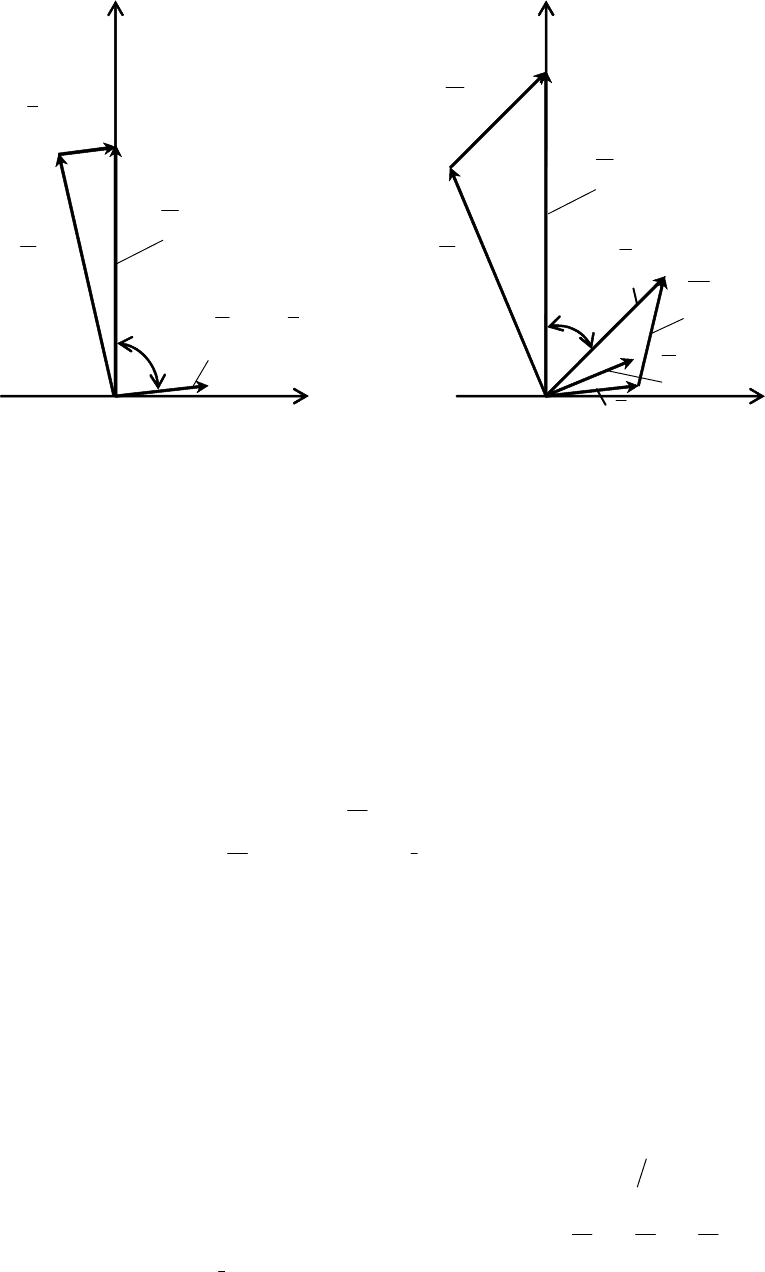
Рис. 6.43. Векторные диаграммы асинхронного двигателя при ска-

лярной IR- компенсации: а – режим холостого хода; б – при наличии

нагрузки на валу двигателя

Несмотря на этот недостаток, разомкнутые структуры частотного

регулирования скорости на основе автономных инверторов напряжения

со скалярной IR–компенсацией находят широкое применение в приво-

дах длительного режима работы с диапазоном регулирования



: 50.

6.2.6. Векторное частотное управление асинхронным

электроприводом с IR – компенсацией

Если вектор напряжения

формируется векторным сложением

напряжения задания

и сигнала

км

kRi  , вводимого с целью ком-

пенсации падения напряжения в фазах

двигателя, то такое

управление называют векторным частотным управлением с IR-

компенсацией. Векторное сложение сигналов производится во времен-

ной области, то есть суммируются сигналы переменного напряжения.

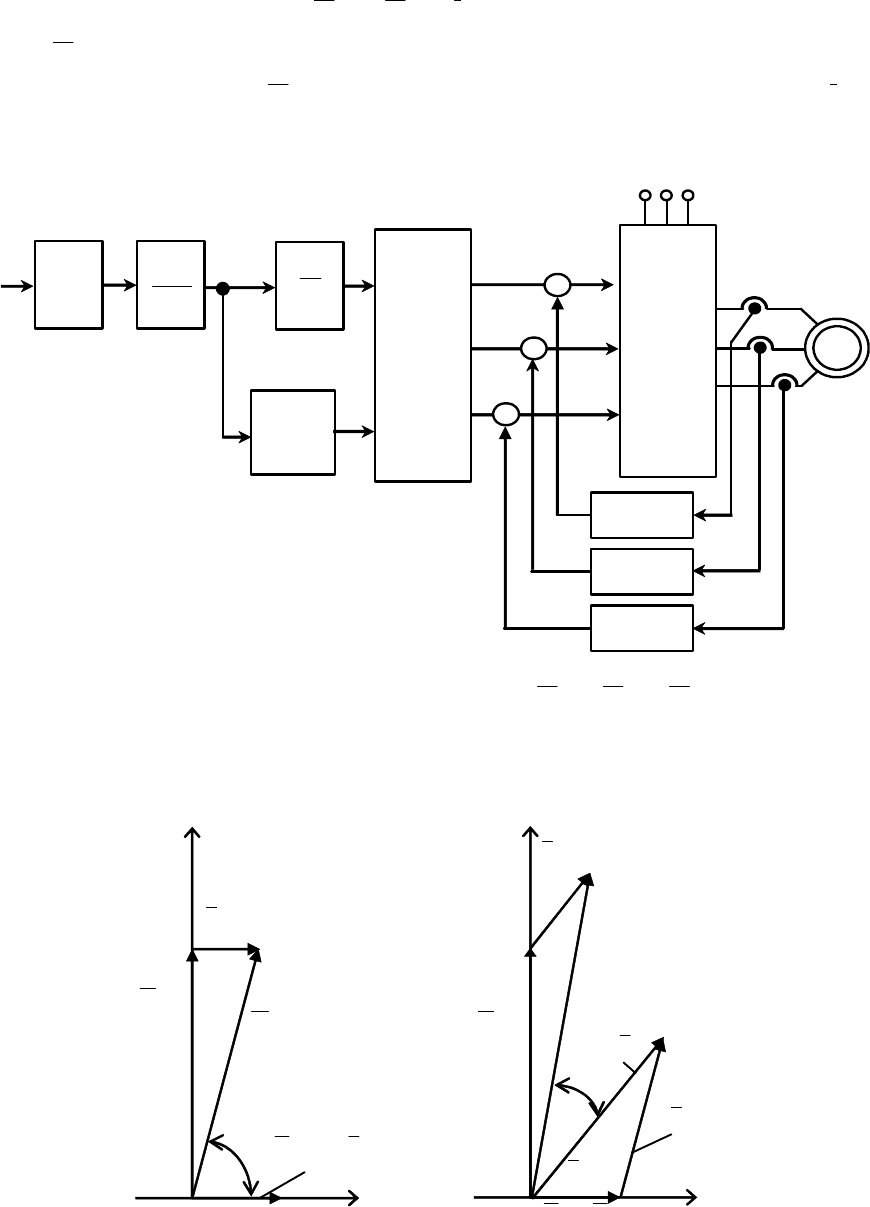
Структурная схема векторного частотного управления с IR–

компенсацией приведена на рис. 6.44.

В схеме (рис. 6.44) на выходе прямого координатного преобразо-

вателя ПКП формируются три синусоидальных напряжения

, сдвинутые относительно друг друга на угол 32



 , с амплитуда-

ми, пропорциональными задающему напряжению

U , и частотой f , оп-

ределяемой законом регулирования. Напряжения

сумми-

руются с сигналами

км

kRi  положительных компенсационных обрат-

ных связей по току в соответствии с выражением

хх1

ψ I

хх1

а)

хх1

RI 



хх1

I



б)

202

км

зу

kRiUU

iii

 , (6.71)

где

– вектор напряжения управления

–й фазой автономного ин-

вертора напряжения;

– вектор напряжения задания

–й фазы;

i –

ток

–й фазы асинхронного двигателя.

Результирующие сигналы управления

формируют

фазные напряжения на выходе преобразователя частоты ПЧ. Векторные

диаграммы асинхронного двигателя при векторной IR–компенсации

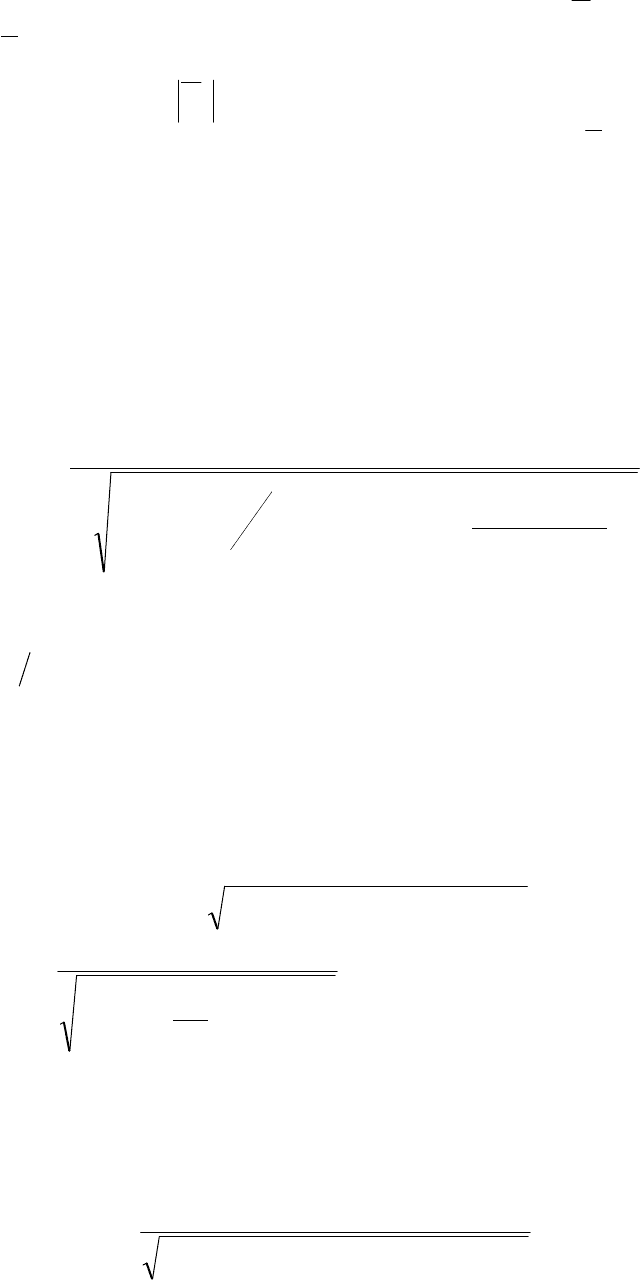
приведены на рис. 6.45.

Рис. 6.45. Векторные диаграммы асинхронного двигателя при век-

торной IR-компенсации: а – режим холостого хода; б – при наличии на-

грузки на валу двигателя

AДТ

СДТ

)АИН(

ПЧ

Рис. 6.44. Структурная схема

векторного частотного управления

асинхронным электроприводом с

IR- компенсацией

ПКП

yx,

ба,

СВА ,,

ПЧН

π2



ЗИ

1км

τ,, Rk

1км

τ,, Rk

1км

τ,, Rk



хх1

1хх

RI 

хх1

1хх

ψ I

хх1

RI 



1хх1

ψψ 

I

хх1

а) б)

203

При векторной IR–компенсации векторы ЭДС

и потокосцеп-

ления

ψ остаются постоянными при изменении нагрузки, а модуль

вектора напряжения

и его фазовый угол меняются. Как показали

исследования, постоянство вектора потокосцепления

ψ способствует

устойчивой работе электропривода. В электроприводах с микропроцес-

сорным управлением векторная IR–компенсация дополнительной на-

стройки, как правило, не требует, то есть при выборе такого закона ре-

гулирования настройка производится по заложенной в электропривод

программе автоматически.

Электромеханическая характеристика, определяющая зависимость

приведенного тока ротора от скольжения для режима неполной IR–

компенсации определяется выражением

1н

2экв1

кн

экв1





































fXs



, (6.72)

где

км

экв

RkRR







> 0 – эквивалентное активное сопротивление цепи

обмотки статора;

н111

fff





– относительная частота;

Н1

f – номинальное значение частоты напряжения статора асинхронного

двигателя;

– регулируемое значение частоты напряжение статора.

Ток статора

I через приведенный ток ротора

I можно найти по

формуле [5]:

sin2



 IIIII , (6.73)

где

кн

экв1

1кн

)(

sin











. (6.74)

Так как регулирование скорости асинхронного двигателя произ-

водится изменением и напряжения обмотки статора, и частоты питаю-

щего напряжения, то ток холостого хода

I можно найти в соответствии

со схемой замещения (рис. 6.39) по следующему уравнению:

1н1σн1

экв1

)(







fXfXR

. (6.75)

204

Механическая характеристика асинхронного двигателя для режи-

ма неполной IR–компенсации, при переменных значениях величины и

частоты напряжения питания определяется выражением



















































1μн

2экв1

экв1

кн0

fXs

RfXs



. (6.76)

При полной IR-компенсации, когда 1

км



k , а 0

экв



R , происхо-

дит регулирование с законами класса const



fE . Механическая

характеристика электропривода представляется выражением

































кн0

fXs



. (6.77)

Критический момент асинхронного двигателя будет равен









1КН0

, (6.78)

а критическое скольжение





1кн

. (6.79)

Механические характеристики асинхронного двигателя, постро-

енные по (6.77) при частотном регулировании скорости и законом регу-

лирования const

*11



, приведены на рис. 6.46.

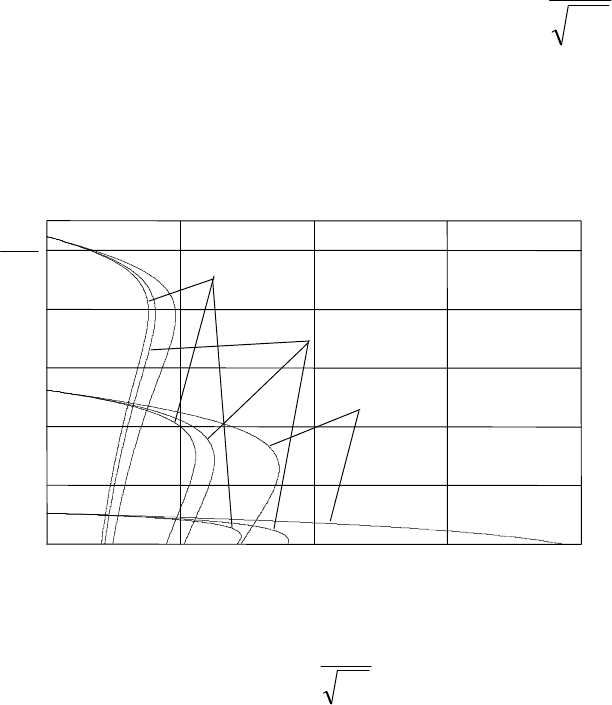
Рис. 6.46. Механические характеристики

асинхронного двигателя при частотном регу-

лировании скорости с IR-компенсацией и за-

коном регулирования const

*11



Как следует из анализа рис. 6.46, при регулировании скорости

асинхронного двигателя с законом регулирования const

*11



(пол-

ная IR–компенсация) критический момент асинхронного двигателя ос-

тается постоянным.

5,0 f

25,0 f

205

Механические характеристики асинхронного двигателя, рабо-

тающего в системе «автономный инвертор напряжения – асинхронный

двигатель с положительной обратной связью по току», рассчитанные по

(6.76) , приведены на рис. 6.47. Частотное регулирование скорости осу-

ществляется в соответствии с законом регулирования const



. Ха-

рактеристики приведены для различных частот

и коэффициентов

положительной обратной связи по току

км

k . С целью наглядного пред-

ставления о регулировании скорости механические характеристики на

рисунке приведены в координатах )ω(





fM .

Рис. 6.47. Механические характеристики асинхронного двигателя

типа 4А112МВ6У3 при частотном регулировании скорости в соответ-

ствии с законом регулирования const



для различных частот

коэффициентов положительной обратной связи по току

км

Анализ характеристик, приведенных на рис. 6.47, показывает зна-

чительное увеличение критического момента асинхронного двигателя

особенно на низких скоростях вращения и увеличение их жесткости.

Из (6.75) следует, что при снижении частоты

напряжения об-

моток статора, ток намагничивания

I возрастает. Увеличится также и

поток намагничивания двигателя. Поэтому для стабилизации потока

намагничивания по мере уменьшения частоты напряжения статора в не-

которых электроприводах коэффициент положительной обратной связи

по току

км

k уменьшают.

100

200

300



рад

км

k

7.0

км

k

2.0

км

k

206

Известно, что положительная обратная связь в контуре регулиро-

вания физической величины не способствует увеличению устойчивости

этого контура, поэтому чем больше коэффициент положительной об-

ратной связи по току

км

k , тем больше будет колебательность электро-

привода. Это подтверждают теоретические и экспериментальные иссле-

дования асинхронных частотно-регулируемых электроприводов с IR–

компенсацией. На рис. 6.48 и рис. 6.49 приведены графики переходных

процессов момента и скорости пуска электроприводов с различными

коэффициентами положительной обратной связи по току

км

k .

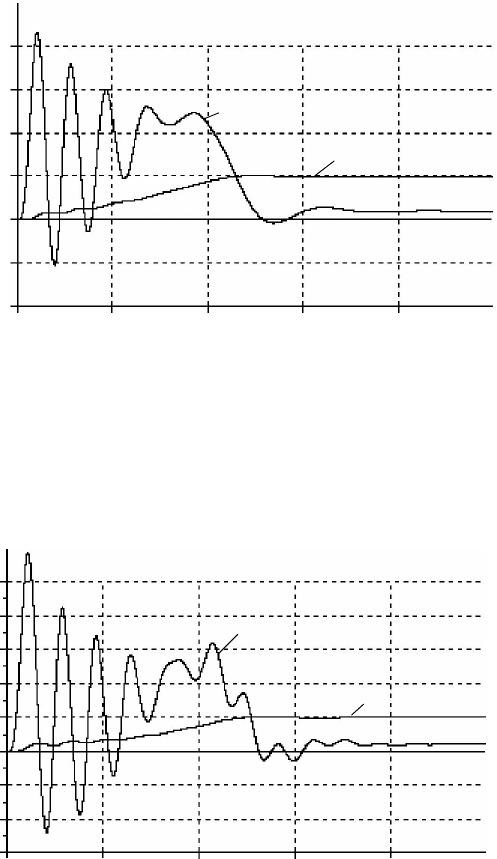
Рис. 6.48. Переходные процессы пуска асинхронного двигателя

на частоту 0,1

max1





f в электроприводе «автономный инвертор на-

пряжения – асинхронный двигатель с положительной обратной связью

по току». 2,0

км1





k , 31415,0

км





Рис. 6.49. Переходные процессы пуска асинхронного двигателя

на частоту 0,1

max1





f в электроприводе «автономный инвертор на-

пряжения – асинхронный двигатель с положительной обратной связью

по току». 7,0

км1





k . 31415,0

км





2

1

.о.е

о.е



M,ω

)τ(ω f



)τ(fM 



0 20 40 60 80

.о.е

)τ(ω f



)τ(fM 



2

1

3



M,ω

207

Анализ переходных процессов скорости и момента рис. 6.48 и

рис. 6.49 показывает, что увеличение коэффициента положительной об-

ратной связи по току с 2,0

км1





k до 7,0

км2





k привело к увеличению

колебательности электромагнитного момента электродвигателя как на

начальном, так и на конечном участках переходного процесса пуска

двигателя. Поэтому при окончательной настройке электропривода по-

стоянную времени

км

T необходимо увеличить, как и рекомендуют ме-

тодики настройки электроприводов «автономный инвертор напряжения

– асинхронный двигатель с положительной обратной связью по току».

Стандартная постоянная времени

км

T контура тока, устанавливаемая в

заводской настройке фирм АВВ, HITACHI, Siemens, Веспер, составляет

0,02 с.

6.2.7. Частотное управление асинхронным электроприводом

с компенсацией момента и скольжения

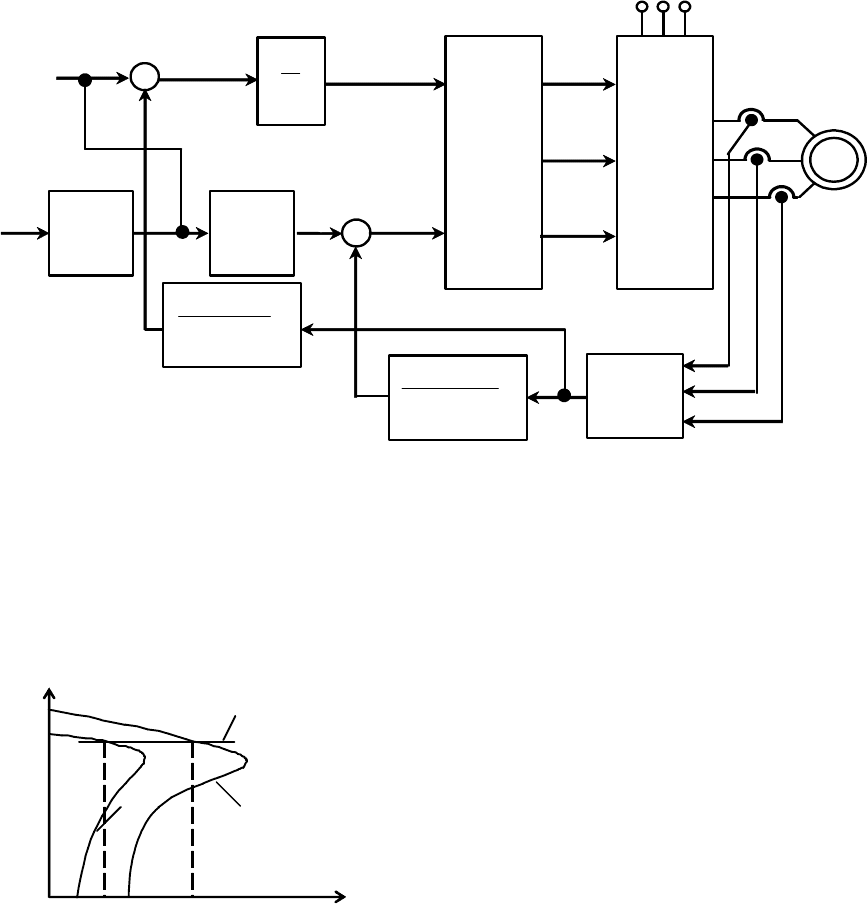
Сигналом тока можно воздействовать как на канал напряжения,

так и на канал частоты. Функциональная схема электропривода с поло-

жительными обратными связями по току в канале регулирования на-

пряжения и частоты приведена на рис. 6.50. При одновременном воз-

действии на канал частоты (компенсация скольжения) и компенсации

момента поддержание скорости на требуемом уровне можно обеспечить

при меньших значениях напряжения

Система электропривода работает следующим образом. Асин-

хронный двигатель работал на характеристике 1 (рис. 6.51) с моментом

на валу двигателя, равным

M . Если момент на валу двигателя увели-

чится и станет равным

M , то возрастет и ток каждой фазы статора

двигателя

i ,

i и сигнал

формирователя тока статора (ФТС).

Увеличится как корректирующее напряжение положительной обратной

связи

кор

U , вычисляемое по выходному току

звеном с передаточной

функцией

)1()(

км

pTkpW







, (6.80)

где

км

k – коэффициент компенсации момента (коэффициент положи-

тельной обратной связи по току в канале регулирования напряжения);

км

T – постоянная времени задержки компенсации момента, так и сиг-

нал положительной обратной связи по частоте

ос

f вычисляемый зве-

ном с передаточной функцией

)1()(

кс

pTkpW





, (6.81)

208

где

кс

k – коэффициент компенсации скольжения (коэффициент поло-

жительной обратной связи по току в канале регулирования частоты);

кс

T – постоянная времени задержки компенсации скольжения.

С ростом сигнала положительной обратной связи возрастает, как сиг-

нал управления

U канала напряжения, что приводит в конечном итоге

к росту фазного напряжения

асинхронного двигателя, так и сигнал

управления

f канала частоты, что приводит к росту частоты

f . Ха-

рактеристика 2 соответствует возросшему фазному напряжению

увеличенной частоте

обмоток статора асинхронного двигателя.

Рис. 6.50. Функциональная схема частотного управления асинхрон-

ным электроприводом с компенсацией момента и скольжения

В результате действия корректирующих положительных обратных

связей электропривод формирует механическую характеристику замк-

нутой системы – 3.

Рис. 6.51. Механические характеристики

электропривода (кривые 1,2) и результи-

рующая характеристика - 3 при наличии

компенсации момента и скольжения





км

1км

ПКП

yx,

ба,

СВА ,,

У1

AДТ

СДТ

)АИН(

ПЧ

ФТС

ЗАД

ПЧН

ПНЧ

кор



кс

кор



209

Анализ характеристик, приведенных на рис. 6.51, показывает, что

в случае дополнительного воздействия на канал частоты можно обеспе-

чить поддержание скорости на требуемом уровне при меньших значе-

ниях фазного напряжения

. Установлено [1], что структуры с ком-

пенсацией частоты оказываются чувствительными к изменению пара-

метров настроек, а с сильной положительной обратной связью могут

оказаться неустойчивыми. В рассматриваемой системе компенсация

момента необходима только в зоне низких значений частот. Поэтому с

ростом задающей частоты

зад

f (или, что то же самое, задающего на-

пряжения

U при дистанционном управлении) коэффициент

км

k можно

уменьшить вплоть до нуля меняя его, например, в функции

зад

f .

6.2.8. Система векторного управления асинхронным электропри-

водом без датчика скорости

В частотно-регулируемых асинхронных электроприводах вектор-

ное управление связано как с изменением частоты и текущих значений

переменных (напряжения, тока статора, потокосцепления), так и со вза-

имной ориентацией их векторов в декартовой системе координат. За

счет регулирования и амплитудных значений переменных, и фазовых

углов между их векторами достигается наиболее качественное регули-

рование скорости, момента и тока асинхронного двигателя, как в стати-

ке, так и динамике. В тех случаях, когда по требованиям технологиче-

ского процесса диапазон регулирования скорости асинхронного двига-

теля не должен превышать

100



применяются бездатчиковые сис-

темы асинхронных электроприводов с векторным управлением. В таких

системах информация о текущих значениях и пространственных поло-

жениях векторов потокосцепления и значениях скорости вращения

асинхронного двигателя определяется косвенно по мгновенным значе-

ниям токов и напряжений фаз двигателя на основе математической мо-

дели асинхронного двигателя. Бездатчиковые системы векторного

управления асинхронным двигателем из-за нестабильности параметров

схемы замещения двигателя уступают системам с прямым векторным

управлением.

Электромагнитный момент асинхронного двигателя можно опре-

делить через произведение вектора



ψ , комплексно сопряженного с

вектором потокосцепления обмотки ротора

ψ , и вектора тока статора

I [7].

Уравнения электромагнитного момента асинхронного двигателя

может быть найдено в следующем виде:

210

 

xyyx

1212

ψψ





 (6.82)

Если сориентировать систему координат по действительной со-

ставляющей потокосцепления ротора

ψ , то мнимая составляющую

вектора потокосцепления ротора

ψ будет равна нулю. В этом случае

момент асинхронного двигателя пропорционален произведению дейст-

вительной составляющей потокосцепления ротора

ψ и мнимой со-

ставляющей тока статора

 



 . (6.83)

На основе выражения (6.83) строятся системы векторного управ-

ления асинхронным электроприводом с ориентацией по вектору пото-

косцепления ротора.

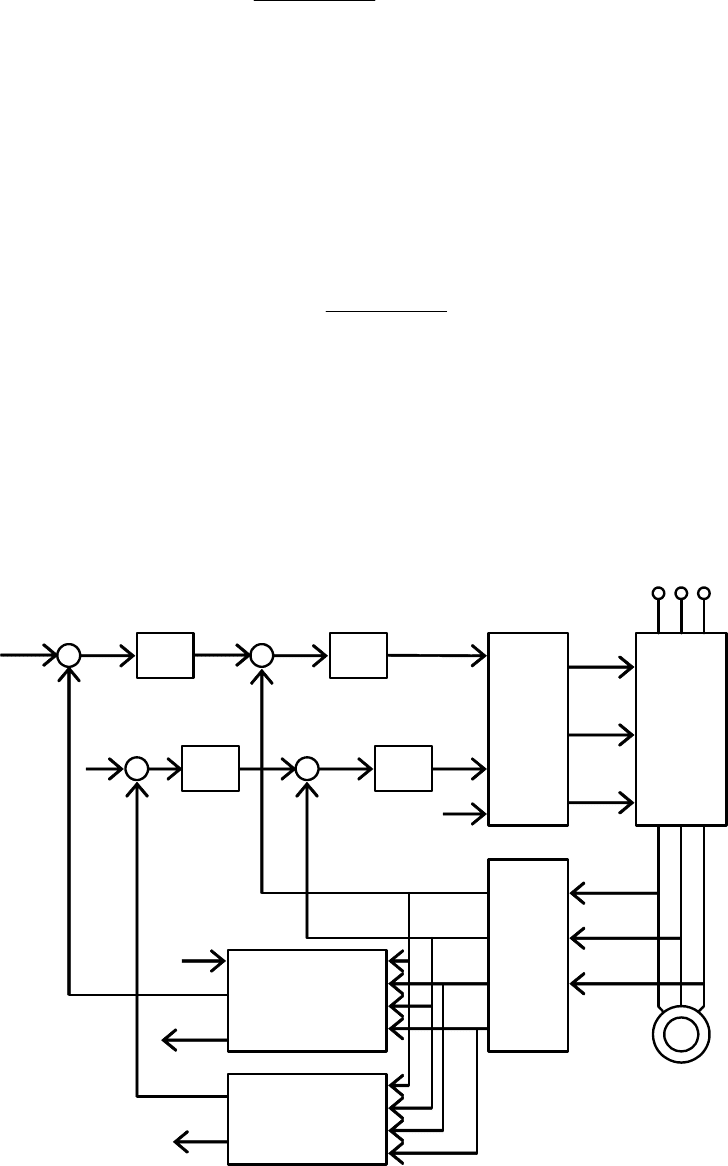
Функциональная схема асинхронного электропривода с бездатчи-

ковым векторным управлением с ориентацией по вектору потокосцеп-

ления ротора приведена на рис 6.52.

Рис. 6.52. Функциональная схема асинхронного электропривода с

бездатчиковым векторным управлением с ориентацией по вектору

потокосцепления ротора

2з

Δψ

РП

1xз

ΔI

РТ

Δω

РC

1yз

ΔI

РТ

1xз

1yз

ПКП

yx,

ba,

CBA ,,

ПЧ

)АИН(



ОКП



UI ,

CBA ,,

ba,

yx,

потока

ьВычислител

положения

скорости и



ос

)(



0ψ

