D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.


4.3.
Networks
of
Automata Without
Any
Letichevsky
Criteria
1 41
of
A in the
following way.
For
every
(a
1
,...,
a
nA
.) € A
n A
, let
)(a
i
,_
1
,x);
moreover,
let
be an
arbitrary
fixed-element
De-
note
by a
o
€ A a
state
for
which
A is
connected.
Let B =
be
a
state-
subautomaton
of the
a
n
-v
1
-Dower
M. of A
generated
bv its
state
(a
n
an}. Then
for
everv
with
,
and
for
every
for
some
A
such that
a
On the
other hand,
8
(an,
(an,
))
generates
an
autonomous state-subautomaton
in
A(X,
if
\p\ n A.
Thus,
for
every
p. q. q' X*
with
I
p\ = n
A
and lql =
\q'\,
8(a
o
,
(
o
,
pq)}
=
Thus,
we
obtain that
B A
with
((a
1
,...,
a
n
A
))
= a
n A
is a
state-
homomorphism
of B
onto
.A.
If
A is not
connected, then considering Proposition 4.22,
we may
assume that
it
can be
represented homomorphically
by a
diagonal product
M.' of its
connected state-
subautomata
and an
autonomous automaton
M.
which
is a
q-product
of A
with
a
single
factor.
We
have already proved that
all
connected state-subautomata
of A can be
repre-
sented
homomorphically
by an
a
o
-v
1
-power
of A.
Obviously,
the
direct
product
of M and
these a
o
-V
1
-powers
is an
a
0
-V
1
-power
of A
which homomorphically represents
the
diago-
nal
product
M
!
. By the
transitive property
of
homomorphic representation, this completes
the
proof.
Now
we are
ready
to
prove
the
following result.
Theorem
4.47.
Let K be a
class
of
automata
without
any
Letichevsky
criteria.
Then
every
general
product
of
factors
from
1C
can be
represented
homomorphically
by an
a
o
-v
1
-product
of
the
same
factors.
Proof.
Let M = A
1
x • • • x
A
n
(X,
again
be a
product
of
automata
A
t
=
(A
t
,
X
t
,
8
t
),
t =
I,...
,n,
(such that each
of
A
t
, t =
1,...,
n, is
without Letichevsky crite-
ria).
Using
Lemma 4.46,
it is
enough
to
prove that
M. can be
represented homomorphically
by
a
diagonal
product
M of
automata such that each
of its
factors
is
either
a
single-factor
product
of an
appropriate factor
of M. or an
a
o
-v
1
-product
of
certain factors
of M.
By
Proposition 4.22,
we can
restrict ourselves
to
proving
our
statement
for the
con-
nected state-subautomata
of M. On the
other hand,
by
Proposition 2.75,
M and
thus
all
of
its
connected state-subautomata
of M
preserve
the
property that they
are
without
any
Letichevsky criteria.
Let
A =
(A,X,
8) be a
connected state-subautomaton
of M. not
having
any
Letichevsky criteria.
If A is
autonomous, then
we are
done
by
Corollary 4.33. Then
we may
assume that
A is
nonautonomous
and
thus
n
A
> 0. Let us
denote
again
by a
o
a
state
for
which
the
(nonautonomous) automaton
A is
connected; moreover,
let a
o
=
(a
o
,1.
•••
a
o,n
),n)
a
o
,t
A
t
, t —
1,...
,n.
Consider
a
complete
list
p
1
,...,
p
u
of all
words
of
length
of n
A
in X*.
By
Lemma 4.37,
D
A
a0)pl
• • •
a
o
,p
u
homomorphically
represents
A. By
Lemma 4.34
and
Proposition 4.32, each
of the
automata
A
ao,pi,
i =
1,...,u,
can be
represented homo-
morphically
by a
diagonal product
of a
single-factor product
of the
factors
of M.
Then
it
is
enough
to
prove that
D can be
represented homomorphically
by a
diagonal product
of
o
V
1
-products
and
single-factor products
of
factors
from
M..

142
Chapter
4.
Without
Letichevsky's
Criterion
Let
x
1
,...,
x
s
be an
arrangement
of the
elements
of the
input
set X. By
Lemma
4.38,
the
diagonal product
B
I,X1
A • • •
B
1,Xs
A • • •
B
nA
,
Xl
A • • •
B
nA
,
Xs
homomorphically
represents
the
automaton
D.
To
complete
our
proof
we now
show that each
of
B
i
,
x
,
i =
I,...
,n
A
,x
e X, can
be
represented homomorphically
by
either
a
single-factor product
or an
a
0
-V
1
-product
of
factors
from
[A
1
,..., A
n
}.
By
Lemma 4.24,
for
every
A
t
=
(A
t
,
X
t
,
t
) e
(A
1
,..., A
n
],
there
are two
possibilities:
(1)
There exist
a
0
, a e A
t
, p, q, q' e X*, \p\ > i - 1, \q\ =
\q'\
>
\A
t
\
- 1
such that
(a
0
,
P) = a and
t
(a,
qr)
t
(a, q'r')
for
every
r, r' e X*, \r\ =
\r'\.
(2)
t
(a,
q) =
t
(a,
q')
holds
for
every
a € A
t
, p, q, q' e X*
having
t
(a
0
,
p) = a, p e
X*,\p\=i-l,\q\
=
\q'\>
\A\-l.
Suppose
that there
is an
automaton
A
t
=
(A
t
,
X
t
,
t
)
[A
1
,...,
A
n
}
having property
(1). Then, applying Lemma 4.39,
we get
B
i
,
x
as a
diagonal product
of
single-factor products
of
A.
In
case
(2) we can
apply Lemma 4.40, assuming that \pu\
> i — 1.
(Then,
by our
assumptions,
there exists
a
maximal positive integer
m
i
,
with
p (x, i,
m,•)
= x.
Moreover,
m
i
-
= | -l| =
|q-l|>0.)
'
This result directly implies
the
following
two
statements.
Theorem 4.48.
Let
1K
be a
class
of
automata
without
any
Letichevsky
criteria.
Then
every
general
product
of
factors
from
K can be
represented
homomorphically
by an
a
o
-product
of
the
same
factors.
Theorem
4.49.
Let K be a
class
of
automata
without
any
Letichevsky
criteria.
Then
every
general
product
of
factors
from
1C
can be
represented
homomorphically
by a
v
1
-product
of
the
same
factors.
4.4
Product
Hierarchies
of
Automata
Theorem 4.49 shows that single links already
suffice
for
homomorphically representing
any
automata
network built
from
automata without
any
Letichevsky criteria.
In
contrast,
we are
going
to
prove that
the
a
o
-V
i
-hierarchy becomes strict
for
homomorphic representation
if
the
component automata
are
permitted
to
satisfy
the
semi-Letichevsky criterion
as we
show
in
this section. Theorem 4.50,
the
main result
of
this
section,
implies even more:
(i) The
v
i
,-hierarchy
is
strict
for the
homomorphic representation.
(ii)
The
a
o
-v
i
,-hierarchy
is
strict
for the
homomorphic representation,
(iii)
The
v
i
,-hierarchy
is
strict
for the
homomorphic simulation.
(iv)
The
a
o
-v
i
,-hierarchy
is
strict
for the
homomorphic simulation.
Let
n 1 be an
integer
and let C
n
=
(C
n
, {x},
n
)
with
C
n
=
{1,...,n}
and
n
(i,
x) = i + 1
(modn)
for all i C
n
.
Thus
C
n
is a
counter with length
n. Let us
consider
the
elevator
2
=
({0,1}, {x
1
, x
2
},
2
) so
that
(0, x
1
) = 0 and
2
(0,
x
2
) =
2
(l,x1)
=
2
(l>
X
2) = 1. We set
/C
= { 2} U {C
p
| p > 1 is a
prime}
and
prove
the
following.
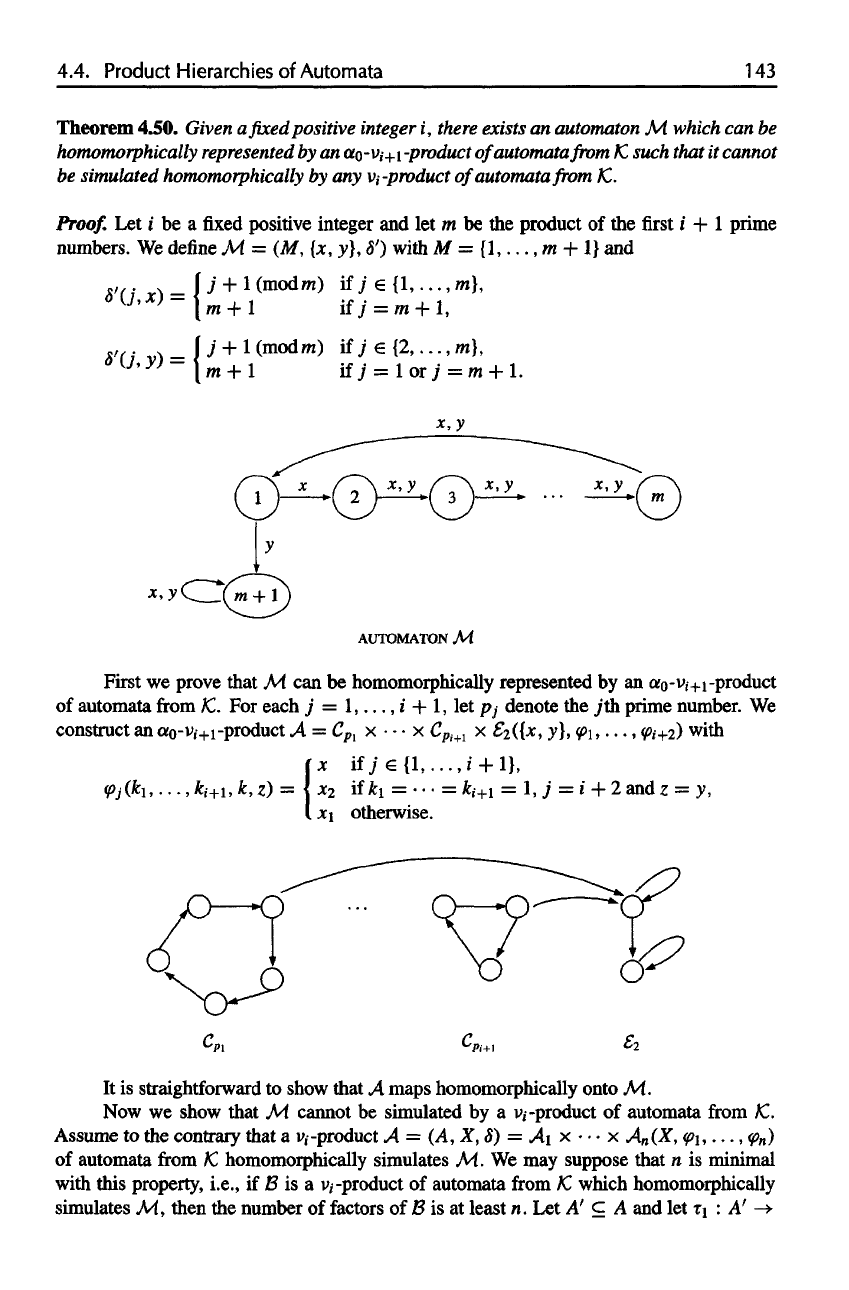
4.4. Product Hierarchies
of
Automata
143
Theorem
4.50.
Given
a fixed
positive
integer
i,
there
exists
an
automaton
M.
which
can be
homomorphically
represented
by an
a
o
-v
i+1
-product
of
automata
from
1C
such
that
it
cannot
be
simulated
homomorphically
by any
V
i
-product
of
automata
from
K.
Proof.
Let i be a fixed
positive integer
and let m be the
product
of the first i + 1
prime
numbers.
We
define
M
with
M =
{1,...,
m + 1} and
First
we
prove that
M. can be
homomorohicallv represented
bv an
an-v
i+1
-product
of
automata
from 1C. For
each
j =
1,...,
i + 1, let p
i
denote
the jth
prime number.
We
construct
an
a
o
-v
i
,
+1
-product
A
with
It
is
straightforward
to
show that
A
maps homomorphically onto
M.
Now
we
show that
M.
cannot
be
simulated
by a
v
i
,-product
of
automata
from 1C.
Assume
to the
contrary that
a
v
i
-product
A = (A, X, 5) = A\ x • • • x
A
n
(X,
1
,...,
n
)
of
automata
from
1C
homomorphically simulates
M. We may
suppose that
n is
minimal
with
this property,
i.e.,
if B is a
v
i
,-product
of
automata
from
1C
which homomorphically
simulates
M,
then
the
number
of
factors
of B is at
least
n. Let A' A and let
1
: A'

1 44
Chapter
4.
Without
Letichevsky's
Criterion
M,
X*
be
mappings such that
1
is
onto
and
for
all a A' and z [x, y},
where
it is
assumed that
We
prove that
m and |
2
(x)|
are
relatively prime. Suppose
the
contrary
and let d be
an
arbitrary prime number which divides
m and |
2
(x)
\.
Because
of the
definition
of
8'
there
exists
a
positive integer
k and
state
a 3 A'
with
8 (a,
2
(x))
km
)
= a
with
1
(a)
{1,...,
m}.
But
then,
by the
structure
of A, d \
2
(x) implies that there exists
a
positive integer
l
such
that
8(a,
(
2
(x))
l
)
= a and d
leading
to S'(
1
(a),x
l
)
=
1
(a),
(a)
{1,...,
m}, a
contradiction.
Therefore,
m and
2
(x))
are
relative
primes.
We
show that
m and I
2
(y)
I
are
relatively prime.
For
this
we
suppose
the
contrary
and
let d be a
prime number which divides
m and
Thend
Therefore,
d
does
not
divide
Because
of the
structure
of M.
there exists
a
positive integer
k, a
state
a € A'
with
and (
But
then,
by the
struc-
ture
of A and d \
there exists
a
positive integer
l
such that
d and
a,
contradicting
(Of
course,
m
and
m
—
d + 1 are
relative primes. Thus, indeed,
Thus
we
obtain that
m and
are
relatively prime.
By
this
observation,
A
also
homomorphically
simulates
M by the
mappings
M and
with
and
Then
we can
also assume
. In
addition,
we may
choose
A'
such that
the
cardinality
of A' is
minimal.
Let us
partition
A' as A'
where
and
A
1
=
If
a A
o
and b A',
then,
by the
minimality
of the
cardinality
of A,
there
is
a
word
u {x, y}*
with 8(a,
2
(u)
= b).
Therefore,
if the jth
component
of a
o
is
equal
to
1 and A
j
=
2
for
some
j —
1,...,n
and a
o
€ a
o
,
then
the jth
component
of a is
equal
to 1 for all a € A'. But
then
we can get rid of the jth
component obtaining
a
v
i
,-product
of
n — 1
factors
that homomorphically simulates
M.
Since this contradicts
the
minimality
of
n we
have that
the jth
component
of a is
necessarily
0 for all a A
o
and j
{1,...,
n]
with
A
J
= 2-
Now
we
show that
for
every
a A
1
there exists
j
{1,...,n} such that
the jth
component
of a is
equal
to 1 and A
J
=
2.
Indeed,
by the
minimality
of the
cardinality
of
A', for
every
a A
1
(=
~
l
(m
+ 1))
there exists
an a
o
€ A
o
such that
for a
suitable
u
{x,
y}*, 8(a
o
,
2
(u))
= a.
Because
of
|n
2
(x)|
=
2
(y), (a
o
,
2
(x )) = a
also holds
whenever
for
every
j
{1,...,n},
A
J
= 2
implies that
the jth
component
of a is 0. But
(a
o,
2
(x
1u1
))
A
o
, a
contradiction.
Now
let a
1
-
l)
be a fixed
state.
We
have 8(a, 2(y))
A
1
, so
that
the jth
component
of the
state 8(a,
2
(y))
is
equal
to 1 and A
J
— £2 for
some
j €
{1,...,n}.
Suppose that
j
really depends
on its
state variables having indices
j
1
,...,
j
t
with
t i.
For
.s =
!,...,*,
define
r
s
= p if A
j;
= C
p
and r
s
, = 1 if A
j
=
2
- Let r be the
product
of the
integers
r
1
,...,
r
n
. It is
clear that
m r.
Thus,
(a,
(
2
(x))
r
)
(q)
with
€
{2,...,
m}.
But
then
the
j
s
th component
of a and 8 (a, (
2
(x))
r
)
are
equal
for all s =
I,...
,t.
Therefore,
the jth
components
of (a,
2
(y))
and
8(a,
2
(x)
2
(y))
are
equal
to 1,
which
contradicts 8(a,
2
(x)
2
(y))
€ A
o
.
This ends
the
proof.

4.5.
Bibliographical
Remarks
145
Let us
summarize some
of the
results
of
this chapter
for
homomorphic representa-
tion
by
automata networks with component automata
from
a
class
K of
non-Letichevsky
automata.
The
a
i
,-product hierarchy collapses
at i = 0 if K is
without
any
Letichevsky
criteria (Theorem 4.48)
and at i = 1 if K
satisfies
the
semi-Letichevsky criterion (Corollary
4.15).
That
is, in
these
two
cases,
no
feedback
at
all,
or
only feedback
of a
component's
own
state
to
itself, respectively,
suffices
to
achieve computationally what
can be
achieved
with
unrestricted feedback. Meanwhile,
the
v.,-product hierarchy (bounding
the
number
of
incoming links
to
components
by i)
collapses
at i = 1
for
automata without
any
Letichevsky
criteria (Theorem
4.49);
moreover, even
a
o
-V
I
-products
suffice
(Theorem
4.47).
Neverthe-
less,
in the
semi-Letichevsky case,
if no
feedback
is
allowed, then
the
number
of
permit-
ted
links
can
determine what
can be
homomorphically represented
or
homomorphically
simulated.
Taking
into consideration that
the
concept
of
homomorphic simulation
is
more gen-
eral than
the
concept
of
homomorphic representation, and, moreover, that
the
concept
of
v
i
,-product
is
more general than
the
concept
of
ao-v
i
[-product,
by
Theorem 4.50,
we can
derive that
33
(1) the
a
o
-v
i
,-hierarchy
is
strict
for
both homomorphic representation
and
homomorphic
simulation,
and
(2)
the
v
i
,-hierarchy
also
has
this property.
The
product hierarchies
for the
Letichevsky case
are
treated
in
detail
in the
next
two
chapters
of
this monograph
(in
particular, Theorems 5.27
and
6.15).
4.5
Bibliographical
Remarks
Section
4.1. Lemmas
4.2 and 4.3 and
Theorem
4.4 are
essentially contained
in
Domosi
and
Gecseg [1992]. Corollary 4.15
is a
consequence
of the
Esik-Horvath
characterization
theorem
due to Z.
Esik
and Gy.
Horvath
[
1983].
The
other parts
of
this chapter
are
essentially
new
but
they
can
also
be
derived
from
the
results
of Z.
Esik
and Gy.
Horvath
[1983].
Some
related results
are in
Esik
[1983].
Section
4.2. These technical observations
on
basic properties
of
automata without
any
Letichevsky criteria
are new but
more
or
less trivial. They
are
necessary
to the
description
of
some results
in
Section 4.3.
Section
4.3. Theorem 4.47
was
obtained
by F.
Gecseg
and H.
Jiirgensen
[1991].
Theorem
4.48 issued
from
Z.
Esik
and Gy.
Horvath
[1983].
Theorem 4.49
is
given
in
Gecseg
and
Imreh
[1987].
The
other results
are
new.
Section
4.4. This section
is
based entirely
on
Domosi
and
Esik
[1990]
and
Domosi, Esik,
and
Imreh
[1989].
These results generalize
the
statements
of P.
Domosi
and Z.
Esik
[1988d].
Some related characterizations
are
given
in
Imreh [1977], Gecseg
[1986],
Domosi
and
Esik
[1987],
Gecseg
and
Imreh [1987a,
1987b],
Imreh
[1988],
Domosi
and
Gecseg
[1989],
Domosi
[1990],
and
Domosi
and
Gecseg
[1992].
33
See
also
the
introductory part
of
this
section.
This page intentionally left blank

Chapter
5
Letichevsky's
Criterion
The
application
of
two-state elements
is
very
often
used
in
engineering technology.
We
will
show that this conventional solution
is not the
only
possibility.
We may
build digital
and
electronic circuits using completely
different
structures.
In
particular, automata having
Letichevsky's
criterion
and
certain
types
of
transformers
(which realize feedback functions)
can be
also considered.
The
conventional methods make
up
just
one
special case where
the
applied
automata
are
two-state
flip-flop
automata
and the
feedback functions
are
elementary
logical units.
This
fact more
or
less
is
well known.
But
using
our
results, many other solutions
can be
derived.
A
further challenge
of
research
is to
determine which ones
are
important
from
the
point
of
view
of
future technologies.
5.1
Homomorphic
Simulation
and the
v
2
-Product
We
start
with
a
simple
observation.
Lemma
5.1.
Let
1C
denote
a
class
of
automata. Every
v1
-product
of
factors
in
1C
is an
a
o
-product
of
loop products
of
factors
in K.
Let
B = (B,
{x', y'},
8
B
) be the
automaton where
B =
{0,1,1',
2} and
Moreover,
let
be
the
automaton with
B
o
= {0,
1,1'}
and
The
following
statement
is
obvious.
147

148
Chapter
5.
Letichevsky's
Criterion
Lemma
5.2.
Consider
a
(general)
power
M =
(B
n
,
X, 8)
of
B.If
a,b B
n
and u X*
with
8(a,
u) = b, and
if
no
component
of
b is 2,
then
no
component
of
a is 2.
Suppose
that
no
component
of
b is 2.
If
\u\ is
even, then
for
each
i .
[n],
the ith
component
of
a is 0 if
and
only
if
the ith
component
of
b is 0.
If
\u\ is
odd,
then
for
each
i
[n],
the ith
component
of
a is 0
if
and
only
if
the ith
component
of
b is in {I,
I'}.
Next
we
prove
the
following lemma.
Lemma
5.3.
If
a
stronslv connected automaton
A is
homomorphically
simulated
bv a
V2-power
,
then
A is
homomorphically simulated
by
some
vl
1
-power
Proof.
Suppose that
a
V
2
-power
M =
(B
n
,
X, S
M
) = B
n
(X,
\
,...,
n
)
homomorphically
simulates
the
strongly connected automaton
A = (A, Y, 8) by the
mappings
\
: A'
A (A'
B
n
),
2
: Y X*. Let D = (V, )
denote
an
appropriate graph
for M
such that
the
in-degree
of
each vertex
is at
most
2.
Since
A is
strongly connected,
we may
assume
that
A' is
strongly connected
in the
following
sense:
For any a, b A'
there exists
a
word
u
Y*
with
8M(a,
2
(u))
= b.
Define
there exists
Then, since
A' is
strongly connected,
the set H is
also
strongly connected,
i.e.,
for
every
pair
a, b H
there exists
a
word
u € X*
with S
M
(a,
u) = b.
Thus,
by
Lemma
5.2,
if the
ith
component
of
some state
in H is 2, for
some
i €
[n],
then
the ith
component
of
each
state
in H is 2.
Moreover,
if for
some
i, j [n]
there exists
(a
1
,...,
a
n
) H
such that
a
i(
= a
j
= 0 or a
i
, a
j
{I,
I'},
then
for all
(b
\
,...,
b
n
) H it
holds that
b
i
= b
j
= 0 or
b
i
,b
j
{l,l'}.
Let i
denote
any fixed
integer with
i €
[n].
Let (y, i), (K, i) E
denote
the two
edges
of D
with target
i.
(Without
loss
of
generality
we may
assume that there
are two
such
edges.)
We
show
how to
define
the
function
i(. We
will distinguish several
cases.
In
each
case,
it
will hold that
if
both
(a
\
,...,
a
n
) and
8j^((a\,..., a
n
),
x) are in H,
then
In
fact,
except
for
Case
1, we
shall even have that
the
letters
i
a
n
, x) are
equal. Moreover,
it
will
be
clear that
the
functions depend
at
most
on a
i
, and one of a
i
, and a
K
. If i € (j, k},
then
we may
take
so
from
now on
we
assume that
i {j, k\.
Case
1. The ith
component
of
some state
in H is 2.
Then
the ith
component
of
each
state
in H is 2. We
define
(a
1
,...,
a
n
) = x' for all
(a
\
,...,
a
n
) B
n
.
Case
2. The ith
component
of no
state
in H is 2 but
there
is a
state
in H
whose
j th or
Kth
component
is 2.
Then
the j th
component
of
each state
in H is 2, or the
k
th
component
of
each
state
in H is 2. For
each
(a
\
,...,
a
n
} B
n
,
define
i
(a\,...,a
n
,
x} =
i
,
(b
1
,...,
b
n
, x),
where (b
1
,...,
b
n
)
agrees with
(a.,...,
a
n
)
except that
b
j
= 2 if the jth
component
of
each state
in H is 2 and b
k
= 2 is the kth
component
of
each state
in H is 2.

5.1. Homomorphic Simulation
and the
v
2
-Product
1 49
Case
3. No
state
in H has its
ith,
jth,
or kth
component equal
to 2. We
divide this
case into three subcases.
Case
3.1.
For all
(a
\
,...,
a
n
) H,
either
a
i
,
= a
j
, = 0 and a
k
€
{1,1'}
or a
i
, a
j
{1,1'}
and a
k
= 0.
Then
for
(a
1
,...,
a
n
) € B
n
,
define
where
(b
1
,...,
b
n
) is
obtained
from
(a
1
,...,
a
n
) by
setting
its jth
component
to 0.
Case
3.2.
For all
(a
\
,...,
a
n
) H,
either
a
i
,
= a
k
= 0 and a,
{1,1'}
or a
i
, a
k
{1,
1'}and
a
j
, =0.
This subcase
is
symmetrical
to the
previous one.
For(a
1
,...
,a
n
)
€ B
n
,
define
where
(b
\
,...,
b
n
) is
obtained
from
(a
\
,...,
a
n
) by
setting
its kth
component
to 0.
Case
3.3.
For all
(a
\
,...,
a
n
) H,
either
a
i
,
= a
j
=a
k
= 0 or
a
i
,
a,-,
a
k
{1,1'}.
For
(a
1
,...,
a
n
) € B
n
,
define
where (b
1
,...,
b
n
) is
obtained
from
(a
1
,...,
a
n
) by
setting
its jth and kth
components
to O.
Since
we
have
S
M
for
all
states
(a
1
,...,
a
n
) € H and x € X
such that
S
M
((a
1
•
•
•,a
n
)x)
€ H, it
follows that
A is
homomorphically simulated
by
B
n
(X,
1
{,...,
( '
n
)
using
the
same mappings
I
: A'
A (A'
B
n
),
2
: Y X*.
Moreover, since each
function
{(a
1
,...,
a
n
, x)
depends
at
most
on a
i
, and one of a
j
and a
k
,
they
define
a
vl
1
-power
of B.
Lemma 5.4.
If
a
strongly
connected
automaton
A is
homomorphically
simulated
by a
v
\
1
-power B
n
(X,
1
\,...,
n
),
then
A is
homomorphically
simulated
by
some v
\
-power
with
m n.
Proof.
Suppose that
a
v
1
-power
M = (B
n
,X,8M)=B
n
(X,
1
'--,
n
)
homomorphically
simulates
a
strongly connected automaton
A = (A, Y, 5) by the
mappings
\
: A'
A
(A'
B
n
),
2
: Y X*. We
need
to
show that
a
v
r
power
B
o
m
(X,
{,...,
'
n
) for
some
m
n
homomorphically simulates
A.
When
A has a
single
state, this
is
clear. Moreover,
we
may
assume that there
is no n' < n
such that
a v
\
l
-power
of B
homomorphically simu-
lates
A.
Let
H = (b € B
n
|
there
exists
b' A', y Y, p, q X* :
2
(y)
= pq,
8
M
(b',
p)
= b).
Suppose that (a
1
,...,
a
n
) € H. If a
i
, = 2, for
some
i €
[n], then since
.A is
strongly connected,
b
i(
= 2 for all
(b
1
,...,
b
n
) H. But
then
n > 1 and A is
homo-
morphically simulated
by
some v
l
1
-power B
n
~
l
(X,
1
'{,...,
n
_
1
), contrary
to our
assump-
tions. Thus,
no
component
of any
state
in H is 2. For
each
i
[n],
(a
1
,...,
a
n
)

1
50
Chapter
5.
Letichevsky's
Criterion
and
x € X,
define
(a
i
, ...,a
n
,x)
=
i(b
\
,...,
b
n
, x),
where
(b\,...,
b
n
) is
obtained
from
(a
1
,...,
n
) by
setting
its ith
component
to 0.
Thus, when
ai,
= 0,
then '
i
(a
1
,...,
a
n
, x) =
i(a
1
,
...,a
n
,
x), and if
a
i{
{1,1'},
then
S
B
(a
i
,
(a
1
,
...,a
n
,
x)) =
8
Bo
(a
i
,
(a\,...,
a
n
, x))
whenever B(a
i
,(
(ai,...,a
n
,
x)) 2.
Since this holds
for all i [
n],
it
follows that
A is
also homomorphically simulated
by
,
completing
the
proof.
Lemma
5.5.
Suppose
that
M =
B
n
o
(X,
\
,...,
(
n
) is a
loop
power,
so
that
its
underlying
graph
is a
cycle.
Suppose
that
(a
\
,...,
a
n
),
(b
\
,...,
b
n
) B
n
o
such that
a
i
, = 0
if
and
only
if
b
i
= 0, i 6
(1,...,«}.
Then
for
every
word
u € X*
whose length
is a
multiple
of
n it
holds
that
a
i
,
= b
i
,
implies
Proof.
Let us
consider
a
loop power
M.
with
the
underlying graph
D = (V,
{(i,
i + l
(mod
n)) | i
V})
and
a
pair(a
1
,...,
a
n
),
(b
\
,
...,b
n
)
€
B
o
having
our
conditions. Suppose that
a
i
= b
i
for
some
i
{1,...,
n}.
Then
i+\
(mod
n)
(a
1
,
• • •, a., x) = (
i+1
(mod
n
)(b
1
,...,b
n
„x)
for
every
x € X.
Therefore,
if
a
i
+1(mod
n)
=
b
i
+1(mod
n)
= 0,
then
the i + 1
(mod n)th components
of 5
((a
1
,...,
a
n
),
x)
and
((b
1
,...,
b
n
„),
x)
coincide.
On the
other hand,
by the
definition
of
B
0,
,
if
a
i+1
(mod
n),
b
i+1(modn)
{1, 1'}
then
the i + 1
(mod n)th components
of
S
M
((a
1
,...,
a
n
),
x) and
M
((b
1
)
• • •.
b
n
},
x) are
equal
to 0. By
these observations,
it is
easy that
for
every word
u
€ X*, the i + \u\
(mod n)th components
of
5x((a
1
,...,
a
n
),
u) and
S
M
((b
1
,
• • •.
b
n
),
u)
are
the
same.
Lemma
5.6.
Let M. = (M, X, M) be a
loop
power
Of
B
o
having
n
factors. Consider
(a
1
,...,a
n
)
B
n
o
with either
a
i
=
a
i+1(mod
n)
= 0 or
a
if
,
a
i+1(modn
)
{1,
1'}
for
some
i
{!,...,
n}.
Consider
a
word
w X*
of
even length.
Then
8j^((a\,..., a
n
),
wz) =
M((a
1
,
• • •
a
n),
z)for
every
z X* of
length
n.
Proof.
Consider
a
loop power
M = (M, X,
S
M
) of B
o
having
n
factors
and a
state
(a
1
,
...,a
n
)
B
n
o
with either
a
i
, =
a
i+1(mod
n
)
= 0 or
a
i,(
,
a
i
,
+1
(
mod
n
) {1, 1'} for
some
i
{1,...,
n}. To
prove
our
statement
we may
assume
i = 1
without
any
restriction.
Let
w
€ X* be a
word
of
even length; moreover,
let
x
1
,...,
x
n
€ X. Put
(a
t
,
1
,...,
a
t,n
)
=
8
M
((a
\
,...,
a
n
),
w
x
i
.
..x
t
),
t =
1,...,
n, and
(a
0
,
1
,
• • •,
a
o
,
n
)
=
(a
1
,
• •
•,a
n
)•
It is
clear
that
flf-1,1 € {1, 1'}
implies
a
t\
= 0. In
this case
a
t
,i
=
S(a
\
,
\
(a
\
,...,
a
n
,
X
2k
+1
• • •
x
t
))
for
every
0 k <
t/2.
Moreover,
a
t
-\,\
= 0
with
a
t
-
\
,
n
= 0
also implies that
a
t t1
=
8(a
\
,
(
(a
1
,...,
a
n
,X
2k+1
• •
-x
t
))
if 0 k <
t/2.
It is
clear that
a
t
,_i,2
€ {1, 1'}
implies
a
t
,i
= 0.
This means that
a
t,2
=
8(a
2
,
2
(a
1
,
• • •
,a
n
,x
2k+1
• •
•*?))
for
every
0
k < (t -
l)/2.
In
addition,
we
have
for t > 1 and 0 k < (t -
l)/2
that
a
t,_1,1
coincides with
8(a
\
,
\
(a
\
,...,
a
n
,
X
2k+\
• • •
*t-1)).
Thus
a
t
-\,2
= 0
also implies that a
t,
2
coincides with
8( a
2
,
2
(a
\
,
...,a
n
,
X
2k+1
• • •
x
t
-1x
t
))
for all 0 k < (t —
l)/2.
Then
we
obtain
by an
induction that
a
t
j =
$(a
j
,
(a\,
• •., a
n
,
X
2k+1
• •
.x
t
-j+\.. .x
t
)
coincide
for
every
1 j t and 0 k < (t
—
j +
l)/2.
This ends
the
proof.
Lemma 5.7.
Let M = (M, X,
8
M)
be a
loop
power
of
B
o
having
n
factors,
If
M
(a,
u
m
) =
a
holds
for
some
a B
o
n
, u X*, and m > 0
such that
the
length
of
u is a
multiple
of
n,
then
_M(a,
u
2
) = a.
