D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.

6.2.
Primitive
Products
and
Letichevsky's
Criterion
171
Formally,
we
define
the
product
N =
A
3n+l
(X,
\
,...,
3n+\)
such that
for any
(a
1
,...,
a
3n+1
)
A
3n+l
,
x X, and t
{1,...,
3n + 1}, we
have
Now we
give
the
formal
definition
of B' and
that
of a
mapping
: B R
,{
r
},i
under
which
R
,{r},i
is an
(y-represented) homomorphic image
of B'.
Let B'
consists
of all b
A
3n+1
for
which there
are (k, p, q) R
,[r},i
such
that
b =
c(u,
k)c(vu
e
~
l
,
k)c(z
ul-1
,
k -
\)e\...
e
n
-
s
+i,
z =
z\...z
s
,
with
z,-
{u
i
,-,
v
i
,},
i
=
1,...,s,
where
e
\
...
e
n
-
s+\
is
defined
as
above,
and q is
represented
by k and
e\...
e
n
-
s
+\
as we ex-
plained. (Recall that
by the
structure
of R
,(
r
},i,
y
n
-
s
+k
• • •
y
n
-s+iu
s
...
u
k+1
y
n
-
2s
+k
• - •
y
n
-2s+1u
s
...
u
k+1
...
y
s+k
...
y
s
+1u
s
...
u
k
+
\
y
k
unambiguously determines
q = y
k
... y
n
whenever
k < 5 and l > 2.
Similarly,
by the
structure
of R
,{r},i>
ys+k
• • •
ys+1u
s
...
u
k+
\y
k
unambiguously determines
q = y
k
... y
n
,
whenever
k < s
and
1 = 2.
Moreover,
q
=
e
n
-
s+1
...
e
k
-
s+1
is
assumed
if k s.)
Furthermore,
let (b) = (k, p, q). It is
routine
work
to
show that
N has a
subautomaton
B'
with state
set B'
which
can be
mapped
ho-
momorphically
by
onto
R
,{r},i-
Finally,
by (b) = (k, p, q), the
last letter
of b is the
same
as the first
letter
of q.
Therefore,
N
y-represents
R
,{r},
1-

1 72
Chapter
6.
Primitive
Products
and
Temporal
Products
Applying
Proposition 2.66
to the
product
N, it is
clear that
we
will
get a
product
N',
which also y-represents
R
,{r},i;
moreover, similar
to N,,
apart
from
the
last factor,
the
feedback functions
of the
factors
of
N"'
really
do not
depend
on
their
last
state variable.
Thus
it is
enough
to
observe that
by an
inductive application
of
Proposition 2.66,
we can
derive
from
the
product
A/"
a
primitive product
M.
In
particular, every vertex
of the
underlying graph
of N has not
more than
two
incom-
ing and two
outgoing edges
in the
resulting product. Moreover,
if
there
is a
vertex with
two
outgoing
edges, then
it is an
element
of a
cycle with
one
edge going into another element
of
the
same cycle,
and all the
other cycle elements have
one
outgoing edge connecting them
with
other elements
of the
cycle.
In
addition, cycle elements have only
one
incoming edge, coming
from
another ele-
ment
of the
cycle.
36
Using Theorem 2.1,
we may
assume that
N is a
primitive product,
for
otherwise
we
could relabel
its
components
by an
appropriate permutation
of
their indices.
This ends
the
proof
of
Lemma 6.6.
We
next prove
the
following lemma.
Lemma
6.7.
Let A be an
automaton
satisfying
Letichevsky's
criterion,
and let
A
k
(X,
( [,
...,
(
'
k
},
k
i
(X,
y'[,...,
( 'i) be
primitive powers
of
A
such
that,
apart
from
the
last
factors,
the
feedback
functions
of the
factors
really
do not
depend
on
their last state variable.
Suppose
that
they
y-represent,
in
order,
R
r
,Hi,d
and
R
T,H
2
,d
for
some
: X
n
A
n
,
HI,
H
2
[p X
+
| |p | =
n}(H
1
,
H
2
are
not
necessarily
disjoint
sets),
and
d 1,
where
n
is
a
multiple
of
s as
before.
There
exists
a
primitive power
M. =
A
k+l+l
(X,
1
,...,
(
k+l+1),
which
y-represents
R-
,Hi\JH
2
,d+\
•
Moreover,
apart
from
the
last
factor,
the
feedback
functions
of
the
factors
of
M.
really
do not
depend
on
their
last
state variable.
Proof.
Define
the
power
A
k+i+l
I
in the
following way.
For any
Clearly, this power
of A is
primitive.
Now
we
consider,
in
order, appropriate homomorphisms
' and \ "
such that
A
k
(X,
{,
..., (p'
k
} y-represents
R
r
,H
1
,d
with respect
to ',
and,
moreover,
A
l
(X,
'{,
...,
£)
y-represents
R
,H
2
,d
with respect
to - ". It is
clear that
t
does
not
depend
on
its
last state variable
if k + l + l.
Therefore,
it is a
routine work
to
show that
the
power
M.
y-represents
R
,H
1
(uH
2
,d+1
with respect
to the
homomorphism having
the
following
properties:
36
The
cycles
may be
wired
in
such
a way
that their
first
element
is
connected
to the
last
one and all the
others
are
connected
to the
previous ones. Then
the
cycles
can
represent clocks
so
that,
for
instance,
if d\ ... d
ms
is a
state
of a
cycle (with
ms
length) representing
the kth
state
of an
arbitrary clock, then
d
2
• • •
d
ms
d\
will represent
its
k + 1
(modms)th state.

6.2. Primitive Products
and
Letichevsky's Criterion
1 73
whenever
(with
\p\ € {0, c}
including
the
possibility
of p = ),
provided
Using
the
definition
of R
<
H,d,
by
Lemma
3.5 it is
obvious that y
1
...
y
d
+n
and are
well
defined.
We
shall
use the
following concept
as
well.
Define
the
subautomaton
R
r
of . ,
x
n
,d
to
have
state
set R d =
R-c,x
n
,d\{(k,
q) I (k, A, q) R
,x\d}' This
is a
subautomaton since
px is a
prefix
of a
word
of X
n
for
every
p € X*
with
|p| < n, x X. For (k, p, q)
R
r
,d,
we
have
|p| = k
always,
so we
will
use the
short
notation
(p, q) for (k, p, q) R
t
d- We
have,
for (p, yq) Rd (y €
{u
t
,
v
t
\ t =
1,...,
s}) and x X,
*.
Let
M = (W x Z,
X.M, 5>j)
be an
automaton with
Y c Z;
moreover,
let B
= (B, X, 5e) be a
subautomaton
of M.
having
a
homomorphism
: B R ,^
onto
R
such that
((M;,
z
)) = (p, yq)
((w,
z) B,
(/?,
yq) €
R
r
,d,
y Y)
implies
z = y.
Then
we
also
say
that
M.
y-represents
R.
T
d
(with respect
to
1/r).
The
following statement
is
obvious.
Proposition
6.8.
Let , : X
n
Y
n
, i =
1,...,
m, be a
system
of
mappings;
moreover,
let
d
be a
positive
integer.
For
any i =
1,...,
m, let Mi =
(W
i
{
x
Z
i
,-,
X,
8,;)
be an
automaton
which
y-represents
R /.
Consider
an
automaton M
m
+\
=
(M
m+
\, X
m+
\,
5
m+
i)
with
X
m+
i
= Y
m
, a
product
U =
R
r,
d
x • • • x
R
Tm,d
x
M
m
+1(X,
\,...,
m
+\) with
Define
the
product
with
Then
M
homomorphically
represents
U.

1
74
Chapter
6.
Primitive
Products
and
Temporal
Products
Lemma
6.9.
Let A = (A, X,
8
A) be an
automaton
satisfying
Letichevsky's criterion
and
let
u =
MI
... u
s
, v =
v\...
v
s
, be any
pair
of
its
control
words.
Consider
an
alphabet
X,
a
multiple
n
of
s
with
n =
ls,l
> \, and a
mapping
: X
n
A
n
having
the
property
\ (p) 6 {u, v}
1
for
each
p € X
n
. For any
integer
d >
\X
n
\,
there
exists
a
primitive
power
M.
of
A
such that
R
Tt
d
is
y-represented
by M.
Moreover,
apart
from
the
last
factor,
the
feedback
functions
of
the
factors
of
M
really
do not
depend
on
their last state
variable.
Proof.
By
Lemma
6.6 and by an
inductive application
of
Lemma
6.7,
we can
prove that
^T,XMX»I
is
y-represented
by an
appropriate primitive power
M' =
A
k
(X,
{,
...,
'
k
)
of
A.
Since
R
,\x
n
\
is a
subautomaton
of
'R-
,x
n
,\x
n
\^
this primitive power
M.'
also
y-
represents
R
)
|x
n
i-
If d =
\X
n
\,
then
M' has the
required conditions. Otherwise,
let
M
=
A
k+i
(X,
1
k+e
)
with£
= d -
\X
n
\
such that
for
any
(a
1
...,
a
k+i
)
€
A
k+t
,
x
X,t
=
l,...,k
+ t,
This power
of A is
primitive
and
y-represents
Tit4.
Lemma
6.10. LetT>=(D,X,
8) and
B=(B,Y,
8') be
automata with
D c 5.
Moreover,
let
: X
n
Y
n
(n > 0) be a
mapping
and
assume that
for a
suitable integer
d > 0 the
following
two
conditions
are
satisfied:
(I)
For all a € B,
(p,q)
e R ,
d
, p X
n
:
8'(a,q)
D
implies 8(8'(a,
q), p) =
8'(a,a
(p))
( D).
Then
there
exists
an a
o
-product
R j x
B(X,
\
which
homomorphically
represents
D)
such
that
(
2((p,
Y)» x)
((p,
yq) R
<
d, x X, y Y)
really
depends
only
on y.
Proof.
Form
the
a
o
-product
C = (C, X, 8") = R ,d x
B(X,
\, (
2
~),
where
for
arbitrary
(p,
yq) € R d (y € Y), b € B and x € X,
\(x)
= x and
2((p,
yq),
x) = y.
Define
the
subautomaton
C'
of
C
with states
C =
{((/?,
yq),
a) € C \
8'(a,
yq) € D} and
input
set
X. We map the
state
c =
((p,
yq),
a)
ofC'
to the
state 8(8'(a,
yq),
p) of D.
Assume
that
C
receives
an
input letter
x in
this state
c. If \p\ < n,
then 8"(c,
x)
=
((px,
q),
8'(a, y)),
which maps
to the
state 8(S'(8'(a,
y),
q), px) =
8(8(8'(a,
yq),
p), x)
of
D, as
required.
If,
on the
other hand,
\p\ = n,
then 8"(c,
x) =
((x,
q
(p)),
8'(a,
y)).
This maps
to
8(8'(8'(a,
y),
qr(p)),
x) in D,
that
is, to
8(8'(8'(a,
yq),
(p)),
x) =
8(8(8'(a,
yq),
p), x),
by
(1)
since
8'(a,
yq) D.
(Observe
in the
second case,
\q\ = d — 1.)
Thus,
the
mapping
\(
(((p,
q), a)) =
8(8'(a,
q), p)
(((p,
q), a)
C',a
D B) is
a
homomorphism
of a
subautomaton
of
C
into
D. By
(2),
is a
mapping onto
D.
Finally,
as
2((p,
yq),
x) = y
((p,
yq)
R
r
,d,
x € X), we
obtain that
2
really depends only
on
y.
This ends
the
proof.
We
shall
use the
following natural extension
of
this result.

6.2. Primitive Products
and
Letichevsky's Criterion
1 75
Lemma 6.11.
Let D = (D, X, 8) be an
automaton.
Consider
a
product
N = (B
1
x • • • x
B
m
, Z*, 5') =
B1
x • • • x
B
m
(Z*,
<pi,...,
m
)
of
automata
B
t
,l t<m, with
D BI x
•
•
-xB
m
.
Let , : X
n
Z
n
(n > 0), 1 i £, be
mappings;
moreover
let : X
n
(Z
l
)
n
wif
,-(
p)
= z
1
f
... z
n
,i,
i =
l,...,£,
wheneverr(p)
=
(214,..., z1,/)...
(z
n
1,...,
Z
n
,/)
5MC/I
that
the
following
two
conditions hold:
(1) For
every
€ D
implies
(2)D
Then f/ie product
V
homomorphically
represents
D,
where
for
each
we
have
and
Proof.
First
we
apply Lemma 6.10, taking
N in the
role
of B.
Consider
the
a
o
-product
U = R
,d
X
N(X,
X
1
X
2
)
given
by
Lemma 6.10
and the
product
V = R
i) d
x
For a
state
)
just defined.
where
given
with
we put
(for
some
h 0, for
each
j = 1,
...,l).
We
write this state
as
Define
an
injective mapping
Denote
by U
(resp.,
y) the
transition functions
of U
(resp.,
V).

176
Chapter
6.
Primitive
Products
and
Temporal
Products
If
\p\ < n, in
8u(((p, yq),
b\,...,
b
m
),
x), the
only changes
are
that
the row of y's is
lost,
p is
replaced
by px, and
b
f
is
replaced
by b\,
which
is b
{
acted
on by
<p
t
<-l
(b\,...,
b
m
,
(y\,
..., yt))
in Bi for i =
1,...,
m,
whereas
in Q of
this state,
the
column
of
y-'s
is
lost
and p
is
replaced
by px,
while
the b's
change
in the
same way.
is
If
where
This shows that
for any
we
have
Therefore,
the
product
U can be
embedded isomorphically into
the
product
V. But by
Lemma 6.10,
U
homomorphically represents
D.
Thus,
V
also
has
this property.
6.3
Homomorphic Completeness
Under
the
Primitive
Product
In
this section,
we
will establish that
a
primitive product
of
Letichevsky automata
can
homomorphically represent
any
finite
automaton
. To
avoid trivialities,
we
note that
it is
enough
to
restrict ourselves
to
cases
in
which
S has at
least three states.
Consider
an
automaton
A
satisfying Letichevsky's criterion
and
let
u =
u\...
u
s
, \
=
v\...
v
s
denote
a
pair
of
control words
for A as
before.
We put U U = U V U = U,
and
so
that
and
are,
respectively,
logical
AND and
logical
OR on the set {u, v}.
First
we
show
the
following technical result.
Lemma 6.12.
Define
the
automata
with
where
for
6.3.
Homomorphic
Completeness Under
the
Primitive Product
1 77
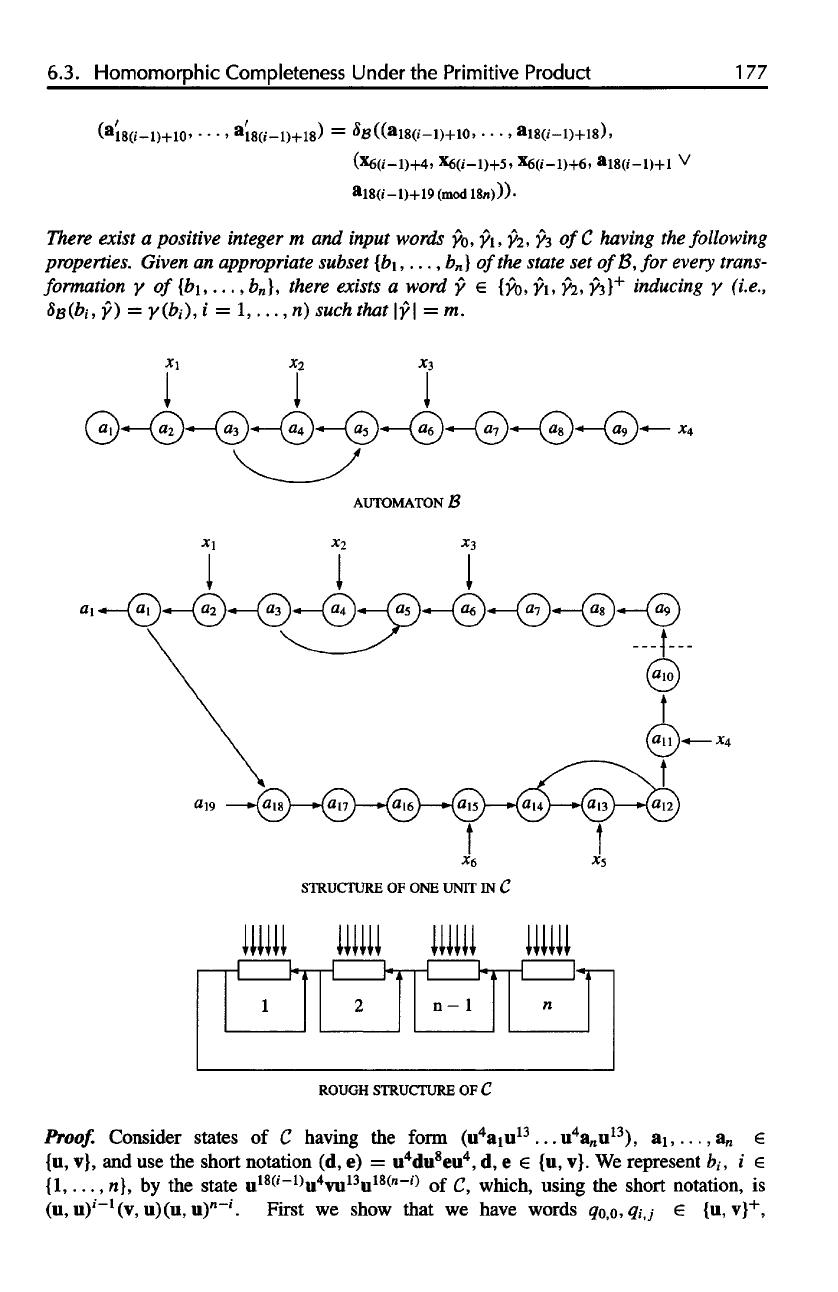
There
exist
a
positive integer
m and
input words y
o
,y
1
,Y
2
,
Y
3
of C
having
the
following
properties. Given
an
appropriate subset
(b\,...,
b
n
}
of
the
state
set
of
B, for
every trans-
formation
r of
there
exists
a
word
inducing
y
such that
Proof.
Consider
states
of C
having
the
form
(u
4
a
1
u
13
.
..u
4
a
n
u
13
),
a
1
,...,a
n
{u,
v}, and use the
short
notation
(d, e) =
u
4
du
8
eu
4
,
d, e € {u, v}. We
represent
i, i
{1,...,
n}, by the
state
U
18(
'~
1)
u
4
vu
13
u
18(n
~
l)
of C,
which, using
the
short
notation,
is
(u,
u)
i-11
,
u)(u,
u)
n
~'.
First
we
show that
we
have words qo,o, qi,./
{u,
v}
+
,

178
Chapter
6.
Primitive
Products
and
Temporal
Products
i
= 1, 2,
3,4,
j =
1,...,
n, all
having
the
same length such that
where
and, otherwise,
Using
the
symmetry
of the
structure
of C to
show
the
existence
of the q 's, it is
enough
to
prove
the
existence
of
go,o
7u {u,
v}
+
,
i = 1, 2,
3,4.
Define
the
following input
letters
(not words!)
of
C:
It
can be
proved
by an
elementary computation that
the
words
go,qo,o
= x
o
y q1,1
=
x1
5x
2
4
,
q2,1
=
x3
5x
4
4
,
q3,1
= 5
9
,
q4,1
= x6
5 x
7
4
satisfy
our
requirements.
(See
the
detailed elementary computation below.)
Put ;
and
use the
short notation
BV
an
elementary computation
we get
that
the
,
which
all
have
the
same length, induce
the
following transformations
YJ
of
{b\,
...,b
n
}:
(The
detailed
computation
is
given
below.)
Using
the
well-known
fact
that
y\,
Y2,
Y3
generate
all
transformations
on the n
element
set
{b
1
,
...,b
n
]
(see also
Proposition
1.5)
and
that
Yo
is the
identity,
we
obtain
our
technical
result.
Proof
of
the
properties
of
qo,o
and
qi1i,
i = 1, 2,
3,4.
The
following detailed elemen-
tary
computation shows that
the
words q0,0
= xo
9
q1,1
=
x1
5x
2
4
q2,1
=
x3
5x
4
4
,
q3,1
=
x
5
9
,
q
4l
=
X6
5
x7
4
satisfy
our
requirements
in the
proof
of
Lemma 6.12:

6.3.
Homomorphic
Completeness Under
the
Primitive Product
1 79
=
c
(u
2
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e3
• .
.u
8
d
n
u
8
e
n
u
6
, x
0
4
)
=
c
(u
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e3
. . .
u
8
d
n
u
8
e
n
u
4
, *
0
3
)
=
c
(u
3
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e3
. .
.u
8
d
n
u
8
e
n
u
5
,
x
0
2
)
=
c
(u
2
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
U
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
,
x
o)
=
(U
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
4
).
(1)
c
(u
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
, x
1
5
x
2
4
)
=
c(u
3
d
1
u
17
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
, x
4
1
x
2
4
)
=
c
(u
2
d
1
u
17
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
6
,
x
1
3
x
2
4
)
=
c
(u
4
d
1
u
14
d
2
u
2
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
, x
1
2
x
4
2
)
=
c
(u
3
d
1
u
14
d
2
u
2
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
5
,
x
1
x
2
4
)
=
c
(u
2
d
1
u
14
d
2
u
2
d
2
u
8
e
2
u
5
d
2
u
2
d
3
u
8
e
3
. . .
u
8
d
n
8
e
n
u
6
, x
2
4
)
=
c
(u
4
d
1
u
11
d
2
u
5
d
2
u
8
e
2
u
2
d
2
u
5
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
, x
2
3
)
=
c
(u
3
d
1
u
11
d
2
u
5
d
2
u
8
e
2
u
2
d
2
u
5
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
5
,
x
2
2
)
=
c
(u
2
d
1
u
u
d
2
u
5
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
,
x
2
)
=
(U
4
d
1
u
8
d
2
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
).
(2)
(5
c
(u
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
,
x
3
5
x
4
4
=
5
c
(u
3
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
,
x
3
4
x
4
4
)
=
c(u
2
d
1
U
8
e
1
U
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
6
,
x
3
3
x
4
4
)
=
5c(ud
1
u
2
d
1
u
5
e
1
u
2
e
1
u
8
d
2
u
8
e
2
u
8
d
3
U
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
,
x
3
2
x
4
4
)
=
c(d
1
u
2
d
1
u
5
e
1
u
2
e
1
U
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
5
,
x
3
x
4
4
)
=
c(u
2
d
1
U
5
e
1
U
2
e
1
u
5
d
1
u
2
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
5
d
1
, x
4
4
)
=
c(u
4
d
1
u
2
e
1
u
5
e
1
u
2
d
1
u
5
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
2
d
1
, x
4
3
)
=
c(u
6
e
1
u
8
d
1
u
5
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
U
8
d
n
u
8
e
n
u
2
d
1
u
2
,
x
4
2
)
=
c(u
5
e
1
u
8
d
1
U
5
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
6
,
x
4
)
=
(U
4
e
1
u
8
d
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
w
u
4
).
(3)
6c(u
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
, x
5
9
)
=
c(u
12
e
1
U
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
,
x
5
8
)
=
c(u
11
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
, x
5
7
)
=
c(u
13
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
4
, x
5
6
)
=
c(u
12
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
,u
8
d
n
u
8
e
n
u
5
, x
5
5
)
=
c(u
u
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
,
x
5
4
)
=
c(u
13
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
4
, x
5
3
)
=
c(u
12
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
, x
5
2
)
=
c(u
n
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
6
,
x
5
)
=
(u
13
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
).
(4)
c
(u
4
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
,
x
6
5
x
7
4
)
=
c
(u
3
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
,
x
6
*x
7
*)
=
5c(u
2
d
1
u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
, x
6
3
x
7
4
)
=
c
(u
4
d
1
u
5
e
1
u
2
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
,
x
6
2
x
7
4
)
=
c(u
3
d
1
u
5
e
1
u
2
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
,
x6x
7
4
)
=
c(u
2
d
1
u
5
e
1
u
2
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
, x
7
4
)
=
c(u
4
d
1
u
2
e
1
u
5
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
, x
7
3
)
=
c(u
3
d
1
u
2
e
1
u
5
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
5
,
x
7
2
)
=
c(u
2
d
1
u
2
e
1
u
5
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. .
.u
8
d
n
u
8
e
n
u
6
,
x
7
)
=
(u
4
(d
1
v
e
1
)u
8
e
1
u
8
d
2
u
8
e
2
u
8
d
3
u
8
e
3
. . .
u
8
d
n
u
8
e
n
u
4
).

1
80
Chapter
6.
Primitive
Products
and
Temporal
Products
Proof
of the
properties
of J (j =
0,1,
2, 3). The
next detailed elementary com-
putation shows that
the j (j — 0, 1, 2, 3),
which
all
have
the
same length, induce
the
transformations
j
of
[b\,..
.,b
n
} given
in the
proof
of
Lemma 6.12.
(0') Identity.
c
((d
1
,
u, . . . , d
n
, u),
q
0
,o)
=
(d
1
,
u, . . . , d
n
, u).
(1') n-cycle.
c
((d
1
,
u, d
2
, u,
d
n
_
1
,
u, d
n
, u), q
1,1
. .
.q
1,1
q1,1
. .
.q
3,n
q
2,1
• •
.92,11)
=
c((d
1
,d
2
,d
2
,
.
..,d
n
_
1
,d
n
_
i
,d
rt
,d
n
,d
1
),q
3,1
...
q
3
,
n
q
2,1
•
-.q2,n)
=
c
((u,
d
2
, u, . . . ,
d
n
_
1
,
u, d
n
, u,
d
1
), q
2
,
1
. . .
q
2,n
)
=
(d
2
,
u, d
3
, . . . , u, d
n
, u, d
1
, u).
(2') Transposition.
c
((d
1
,
u, . . . , d
n
, u),
91,192,191,2
• • •
q
1
,
n
q
3,1
• • •
q
3
,
n
q
2,1
• • •
q2,n
(q1,1
• • •
q
1,1
q
3,1
• • •
q
3,n
q
2,1
• • •
q
2
,
n
)
n-1
)
=
c((d
1
,
d
2
, d
2
, u, d
n
, u),
92,191,2
• • •
9
1
,
n
q
3,1
• • •
q
3
,
n
q
2,1
• • •
q2,
n
(q1,1
• • •
q
l,n
q
3,l
• • •
q
3,n
q
2,l
• • •
q
2,n
)
n-1
)
=
c((d
2
,
d
1
, d
2
, u, d
3
, . . . , u,
d
n
_
1
,
u, d
n
, u),
q
1,2
. . .
q
1
,nq
3
,
1
• • •
q
3,n
q
2,1
• • •
92,n
(q
1,1
• • •
q
1,n
q
3,1
• . .
q
3,n
q
2,1
• • •
q
2,n
)
n-1
)
=
c((d
2
,d
1
,d
2
,d3,d
3
,
...,d
n
_
1
,d
n
_
1
,d
n
,d
n
,d
2
),q
3,1
...q
3
,
n
q
2,1
•••q
2
,
n
(91,1
• • •
q
l,n
q
3,l
• • •
q
3,n
q
2,l
• • •
q
2,n
.)
n-1
)
=
c
((u,
d
1
, u, d
3
,
d
n
_
1
,
u, d
n
, u,
d
2
), q
2
,
1
. . .
q2,
n
(q1,1
• • •
q
l,n
q3,l
• • •
q
3,n
q
2,l
. • •
q
2.n
)
n-1
)
=
5((d
1
,
u, d
3
, u, u, d
n
, u, d
2
, u),
(q
1,1
. . .
q
1
,
n
q
3,1
. . .
q
3,n
q
2,1
• • •
q
2,n
)
n-1
),
and
now
applying
the
n-cycle operation
n — 1
times,
we
obtain
((d
1
,
u, d
3
, u, , u, d
n
, u, d
2
, u), (0
U
. . .
q
1
,
n
q
3,1
• • •
q
3,n
q
2,1
• • •
q
2,n
,)
n-1
)
=
(d
2
,
u, d
1
, u, d
3
, . ,
d
n
_
1
,
u, d
n
, u).
(3') Collapsing.
c
((d
1
,
u, d
2
, u, d
3
, , d
n
, u), q
1
,1q
3
,2q
4
,
1
q
2,1
q
3,1
92,1)
=
c((d
1
,
d
2
, d
2
, u, d
3
, . . . , d
n
, u),
93,294,192,193,192,1)
=
c
((d
1
,
d
2
, u, u, d
3
, . . . , d
n
, u),
q
4,1
q
2,1
q
3,1
q
2,1
)
=
c
((d
1
v d
2
, d
2
, u, u, d
3
, d
n
, u),
q
2,1
q
3,1
q
2,1
)
=
c
((d
2
,
d
1
v d
2
, u, u, d
3
, d
n
, u),
93,192,1)
=
c
((u,
d
1
v d
2
, u, u, d
3
, . , d
n
, u),
q
2
,
1
)
= (d
1
v d
2
, u, u, u, d
3
, , d
n
,
u).
Now
we are
ready
to
prove
our key
result
for
this section.
Theorem 6.13.
Let A = (A, XA, A) be an
automaton
satisfying
Letichevsky's
criterion.
For
any
automaton
£
there
exists
a
primitive power
P
of
A
such that
can be
represented
homomorphically
by P.
Proof.
Let u = u
I
...u
s
,
v =
v
1
...
v
s
denote
a
pair
of
control words
of A as
before.
Consider
an
integer
n > 3 and
define
the
power
N =
A
18ns
(X
N
,
p
1
,...,
p
18ns
)>
X
N
=
A
6n
,
of A in the
following manner.
For any
state
(a
1
,...,
a
18ns
)
e
A
18ns
, input
