D?m?si P., Nehaniv C.L. Algebraic Theory of Automata Networks. An Introduction
Подождите немного. Документ загружается.

6.4. Temporal Products
191
If
k
contains
a
nonpermutation automaton
A
4
=
(A
4
,
X
4
, 4),
then there
are a
1
, a
2
e
A4,
x € X
4
with
a
1
a
2
and
(a
1
,
x) = (a
2
, x).
Then
for any
pair
b
m+t
(u)
b
m+t
(v)
e
B
m+t
,
t =
1,...,
m, 1 <
M
< v < m + 1, let us
give
a z e
{1,...,
r]
with
D
z
= A
4
and
{d
z
,
d'
z
]
=
{a
1
, a
2
}, where
d
z
and d'
z
denote
the zth
components
of
b
u
m+t
and
b
v
m+t
,
respectively. Thus
we
obtain
b
u
m+t
b
v
m+t
; moreover, since
p
z
(x')
= x (x' € X) we do not
get
a
contradiction assuming (b
u
m+t
,
x
u
) =
(b
v
m+t
,
x
v
) =
b
m+t
(by y
2
= x
u
=
x
v
). Thus
we
have obtained (2a).
In
addition,
let .As =
(A
5
,
X
5
,
5
) e
1C
be a
nonautonomous permutation automaton,
where
1C
is a
class
of
permutation automata. There
exists
a
triplet
a e A
5
,
;x,
y e X
5
with
85(a,
x) (a, y). It is
clear that
for
some pair k,l,
> 1 of
integers,
(a, x
k
) =
5(a,
y
l
) = a.
Thus there
can be
found
a
positive integer
t
such that
r < k, I and
5
(a, x
k-t
)
5
(a, x
£-t
)
and
5
(a,x
k
-
f+1
)
=
5
(a,
y
l-f+1
).
In
other words,
for a
suit-
able pair
a
1
, a
2
€ A we get a
1
a
2
and
5(01,
x) =
85(a
2
,
y).
For
every pair
b
l
m+t
,
b
2
m+t
e
B
m+t
,
t =
1,....
m, let us
give
a z e {2 r}
with
Dz = As
and{d
z
,
d
z
} =
{a
1
,
a
2
],
whered
z
,
d
z
denote
the zth
components
of
b
m+t
(1)
,
b
m+t
2)
,
in
order. Then,
by the
choices
P
Z
(XI)
= x,
p
z
(x2)
= y we get
b
1
m+t
b
2
m+t
and
that
the zth
components
of
8(b
1
m+t
,
x
1
) and
(b
2
m+t
,
X
2
)
are
equal.
Now
we
suppose that
D
w
= A
5
,
p
w
(x
1
)
= x,
p
w
(x
2
)
= y,
{d
w
,d'
w
}
=
{01,02}
whenever
the
state vectors
b
m+t
(1)
,
b
m+t
(2)
have
different
toth components
d
w
and d'
w
for
some
w; e
{l,...,r}.
Then
we may
assume (b
1
m+t
,x
1
)
—
(b
2
m+t
,X
2
)
=
b
m+t
and
x
1
=y
1
,x
2
=
y
2
by(3a).
Finally,
to
have
the
conditions
x\ = yi and
X2
= y2 in
(3a),
let v e {1, . . . , r} be
not
necessarily
different
from
w
with
Dv = As,
(p
v
(yi)
= x,
(p
v
(y2)
= y,
respectively,
and
let the uth
component
of
every b
t
,t
= 1, . . . , m, be a
suitable state
a e AS
with
85
(a, x)
8$(a,
y).
Then
it is
clear that
we can
suppose
x\ = yi and
KI
= y
2
. D
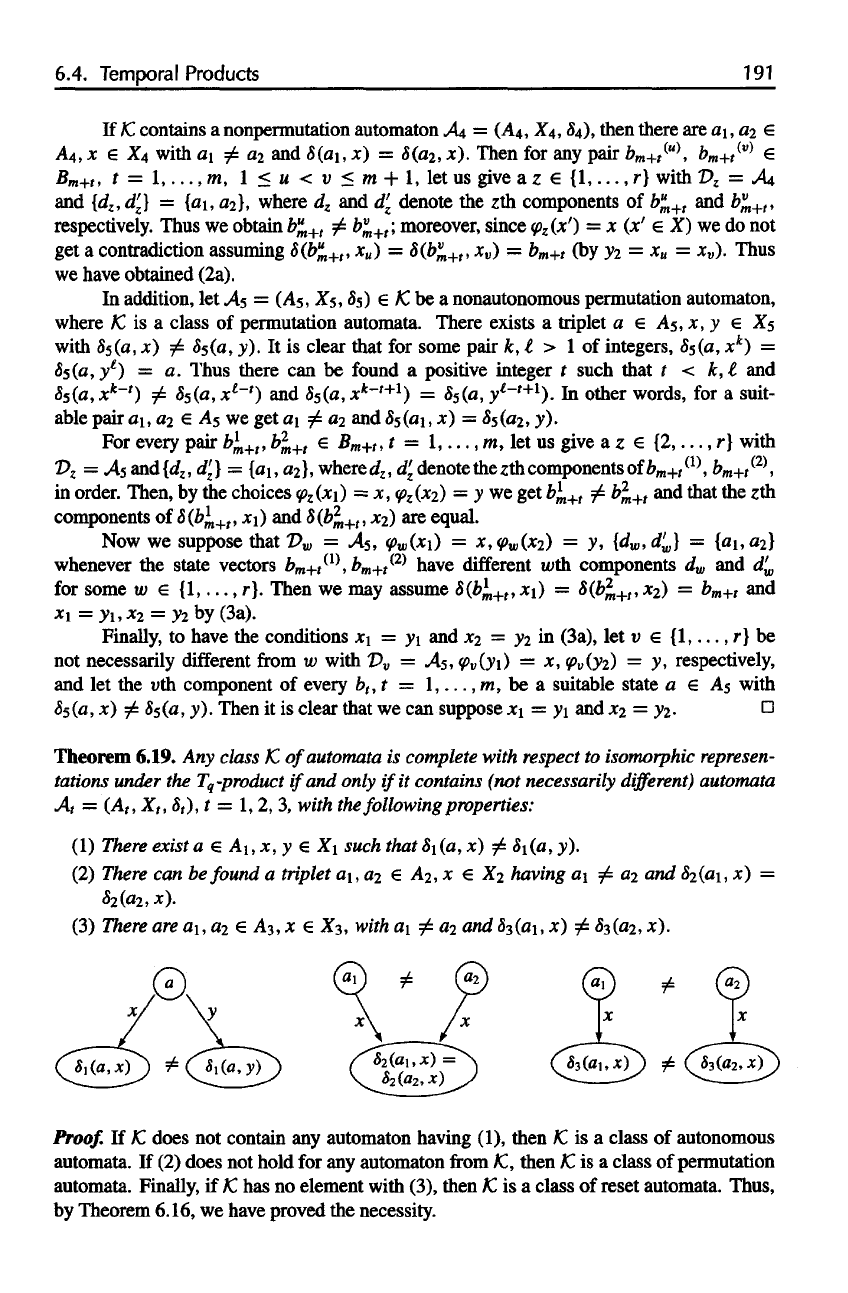
Theorem
6.19.
Any
class
K,
of
automata
is
complete
with
respect
to
isomorphic
represen-
tations
under
the
T
q
-product
if
and
only
if
it
contains (not
necessarily
different)
automata
A
t
=
(A,,
X
t
,
5
t
),
t = 1, 2, 3,
with
the
following
properties:
(1)
There
exist
a € AI, x, y e X\
such that
(a, x) £
8i(a,
y).
(2)
There
can be
found
a
triplet
a\,ai
€ A2, x e Xi
having
a\
82(02,
x).
(3)
There
are a\, ai € A
3
, x e ^3,
with
a\ ^ a
2
and
83(01,
x) ^
83(02,
x).
02
and
82(01,
x) =
Proof.
If /C
does
not
contain
any
automaton having (1), then
fC
is a
class
of
autonomous
automata.
If (2)
does
not
hold
for any
automaton
from
/C,
then
JC
is a
class
of
permutation
automata. Finally,
if
1C
has no
element with (3), then
1C
is a
class
of
reset automata. Thus,
by
Theorem 6.16,
we
have proved
the
necessity.

192
Chapter6. Primitive
Products
and
Temporal
Products
To
show
sufficiency,
we
show that
if
1C
fulfills
conditions
(l)-(3),
then
1C
is
complete
with
respect
to
isomorphic representations under
the T
q
-product.
By
Lemma 6.17
it is
enough
to
show that
for any fixed
nonvoid
finite set A
there
is an
automaton
A/"
€ P
q
(K)
having
A €
SP
t
I(W)
for all A = (A,
[yi, y
2
},
8
A
)
with 8
A
(a,
yi) = a, a € A.
By
our
condition (1),
we get
condition
(1) of
Lemma 6.18. Moreover,
(3) is the
same
as
condition
(2) of
Lemma 6.18.
In
addition,
by
(1), there
is a
nonautonomous automaton
in /C;
furthermore,
by (2) the
class
fC
has a
nonpermutation automaton. Thus conditions
(la)
and
(2a)
of
Lemma 6.18 also hold. Using these facts, consider
an
automaton
N =
(N,
{yi, y
2
},
8) as in
Lemma 6.18
and a
bijective mapping
h : N -> N
such that
for
every
t
=
1,...,
m,
h
-1
(b
t
)
=
b
m+t
,
h
-1
(8(b
t
,
y
1
) e
B
m+t
\(b
m+t
};moreover,/!
-1
(
(b
t
, y
2
))
€
B
m
+t
\
{b
m+i
} whenever
8
A
(a
t
,
y
2
) = at, t =
1,...,
m. Let M' = (N,
{yi, y
2
},
5') be an
automaton (state-isomorphic
to
JV)
for
which
8
f
(h(b),
x) =
h(8(b,
x)),
b e N, x e
{yi, y
2
}.
Construct
the
temporal product
M. = (N,
{yi, y
2
},
M) =
A/"
x
N'({y\,
y
2
},
(p)
such that
<P(yi)
=
(yi,
yz) and
(y
2
)
=
(y
2
, y
2
). Suppose
8
A
(a
t
,
y
2
) = a
£
for a fixed t €
{1,...,
m}.ThenwegetSM(fc,,y2)
=
8'(8(b
t
, y
2
),
y
2
) =
W^),
y
2
) =
h(8(b'
m+l
, y
2
))
=
h(b
m+
i)
= b
t
,
where /4
+£
€
B
m+l
\
{b
m+f
}.
Similarly,
8
M
(b
t
,
yi) =
<5'(<5(£
r
,
y
1
, y
2
) =
8'(h(b'
m+t
),
y
2
) =
h(8(b'
m+t
, y
2
))
=
A(fc
m+f
)
= b
t
,
where
b
+r
e
B
m+t
\
{b
m+t
}.
It can be
easily seen that
g : A
—>
N
defined
by
g(a
t
)
=
b
t
,t
=
1,...,
m, is a
state-isomorphism
of
A
onto
a
subautomaton
of N.
Therefore,
A €
SP
t
IP
q
(1C).
By
the
proof
of
Theorem 6.19
we
have also shown
the
following statement.
Theorem
6.20.
Let
1C
be a
class
of
automata
containing
a
nonreset element.
1C
is
complete
with
respect
to
isomorphic
representations
under
the
T
ao
-product
if
and
only
if
it is
complete
with
respect
to
isomorphic
representations
under
the
T
q
-product.
By
the
proof
of
Theorem 6.19
we
have proved that
if
1C
does
not
satisfy
(l)-(3)
of
Theorem 6.19, then
1C
is
either
a
class
of
autonomous automata,
a
class
of
permutation
automata,
or a
class
of
reset automata, respectively.
It is
clear that these classes
of
automata
are
closed with respect
to the
homomorphism. Thus
we can
derive
from
Theorem 6.16
and
Theorem 6.19
the
following.
Theorem
6.21.
Any
class
1C
of
automata
is
complete with
respect
to
isomorphic
repre-
sentations
under
the
T
ao
-product
if
and
only
if
it is
complete with
respect
to
homomorphic
representations
under
the T
-product.
Now we
start
a
complete characterization
of T
(1C)
(and
T
q
(1C))
for any
class
1C
of
automata.
If a
given class
1C
of
automata
(or any
member
of
1C)
has a
number
of
special
properties, then
we
list them.
In
this way,
we may
omit many
new
definitions.
(In
this sense,
for
example,
we
speak about monotone reset automata, autonomous permutation automata,
etc.)
Theorem 6.22.
If
1C
is a
class
of
autonomous reset automata which contains
a
nontrivial
automaton,
then
T
(lC)
=
T
q
(K)
is the
class
of
all
autonomous reset automata.
If
1C
is a
class
of
trivial automata, then
T (K) =
T
q
(lC)
is the
class
of
all
trivial automata.

6.4. Temporal
Products
193
Proof.
Let A and B a
pair
of
autonomous reset automata, where
A is
nontrivial.
It can be
easily seen that there exists
a
quasi-direct power
of A
having
a
subautomaton isomorphic
to B. It is
also
clear
that
any
class
of
autonomous
reset
automata
is
closed
under
the
general
product,
the
oro-product,
the
quasi-direct product, homomorphism, isomorphism,
and the
temporal product. Thus
it
remains
to
show that
T
(/C)
=
T
q
(1C)
holds
for any
class
of
trivial automata.
But
this statement
is
obvious.
Theorem
6.23.
If
1C
is a
class
of
autonomous
permutation automata
and
1C
has a
nondiscrete
automaton
with
at
least
two
states, then
T
(1C)
= T
q
(1C)
is the
class
of
all
autonomous
per-
mutation
automata.
If
1C
is a
class
of
discrete
automata containing
a
nontrivial automaton,
then
T
ao
(1C)
= T
q
(1C)
is the
class
of
all
discrete automata.
Proof.
It is
clear
that
for an
arbitrary
class
1C
of
discrete
automata,
T
q
(1C)
is a
class
of
discrete automata with
T
ao
(1C)
= T
q
(1C).
Moreover,
it is
easy
to
show that SIP
q
(1C)
contains
all
discrete automata provided that
1C
is a
class
of
discrete automata having
a
nontrivial
automaton. Therefore,
the
second part
of our
theorem holds.
It is
also obvious that
T
q
(1C)
is a
class
of
autonomous permutation automata with
T
ao
(JC)
=
T
q
(1C),
whenever
1C
is a
class
of
autonomous permutation automata.
It
remains
to
show that
if
this
1C
has a
nondiscrete automaton, then
T
q
(1C)
is the
class
of all
autonomous
permutation automata. Observe that
for any
nondiscrete (autonomous) permutation
au-
tomaton
T>
e K we get (1) and (2) of
Lemma 6.18. Therefore,
for
every positive integer
m
there
can be
found
an M = (N, X', 8") €
P
q
(1C)
and, moreover, pairwise disjoint sets
BI,
...,
B
2m
c N and x e X,
such that
B, =
[b
t
, 8(b
t
, x)},
B
m+t
=
[b
m+tj
8(b
m+t
,
x)},
t =
1,...,
m,
with
|
ZB1|
= • • • =
|5
2m
|
= 2.
(A/"
is
autonomous; therefore
we can
sup-
pose
s = 1 and y
l
= y
2
= x\ = •-• = x
n
= x.) Let A =
({a\,...,
a
m
},
X, 8^) be any
autonomous permutation automaton having
m
states. Give
the
mapping
h : N -> N
with
h(8'(b
m+t
,
x)) = b
t
, t €
{1,...,
m}, and
h(b
m+i
)
=
8'(b
t
,
x)
whenever 8(a
t
,
x) = at, t €
{1,...,
m}, x € X.
(The latter
condition
does
not
lead
to a
contradiction
because
of the
fact
that
.A
is an
autonomous permutation automaton.) Construct
the
automaton
N' = (N, X, 8")
(which
is
isomorphic
to N)
such that
for any b' e N let
8"(h(b'),
x) =
h(8'(b',
x)),
x e X.
Take
the
temporal product
M = (N, X, 8
M
) = Af x
N'(X,
(p)
with
(x) =
(x,x),x
e X.
It
can be
immediately seen that
by
8^(a
t
,x)
=
al,t
e
{!,...,m},x
e X, we get
8
M
(b
t
,x)
=
8"(8'(b
t
,x),x)
=
8"
(h(b
m+i
),
x) =
h(8'(b
m+i
,x))
= b
t
.
Therefore,
A
can
be
embedded isomorphically into
M.
Thus
T
q
(1C)
contains
all
monotone permutation
automata.
The
proof
is
complete.
Theorem 6.24.
Let
1C
be a
class
of
autonomous automata which
has
(not necessarily
different)
automata
A
t
=
(A
t
,
X
t
,8
t
),
t =
1,2,
as
follows:
(1)
There
is a
triplet
ai,a2
€
AI,X
e X
1
with
a
1
^=a2and8\(a\,x)
=
(a
2
,x).
(2)
For
suitable
a
1
, a
2
G A
2
and x e X
2
, a\ a
2
and
2
(«i,
x)
2
(a
2
,
x).
Then
T
UQ
(K)
=
T
q
(K)
is the
class
of
all
autonomous automata.
Proof.
Let A = (A, X, 8) be any
autonomous automaton.
We
shall show
A e
T
q
(1C).
Take
an
arrangement
a\,...,
a
m
of the
elements
of A and let N = (N, X, 8') be an
autonomous

194
Chapter
6.
Primitive
Products
and
Temporal
Products
automaton
having
the
following
properties:
there
are
pairwise disjoint sets
B
1
, . . . ,
N,
where
(la) \B
t
\
= 2,
\B
m+t
\
= m + U = 1, . . . , ro;
(2a)
for
a
suitable
b
t
e B
t
, B
t
=
[b
t
, 8'(b
t
, x)},
t = 1, . . . , m, x e X;
(3a)
there
is a
b
m+t
e
B
m+t
such that
for
every
b^
+t
e
B
m+t
\
{b
m+t
}
it
holds that
&'(b
(
m+t>
x) =
b
m+t
,
t =
l,...,m,xeX.
Now
let h : N -» N be a
bijective mapping with
h(b
m+t
)
= b
t
and
*'fo,
*), €
5
m+
,
\
{b
m+t
},
t =
l,...,m,
if
5(0,,
x) =
at,le{l
t
...,
m}, x e X.
Similar
to the
proofs
of
Theorems 6.19
and
6.23,
we
construct
an
automaton
AP =
(N,
X,
8")
(wtochisisomorptoctoAOsuchthatforanyfc'
e N,
8"(h(b"),
x) =
h(8'(b', *)),
x
€ X.
Take
the
temporal product
M = (N, X, 8
M
) = N x
AT'(X,
)
such that
(x) =
(x,x),x
e X.
Then
for an
arbitrary
fixed t e
{!,...,
m},
8
A
(a
t
,x)
= at, a
t
e A,
implies
8
M
(b
t
,
x) =
8"(8'(b
t
,
x), x) =
8"(h(b
(
»
+t
),
x) =
h(8'(b
(1)
t
,
jc))
=
h(b
m+i
)
= b
t
,
where
b(
1)
+i
e
B
m
+i
\
{b
m
+l}.
It can be
seen directly that (h
1
,
h
2
)
with
h
1
: A -*• N,
hi(a
t
)
=
b
t
,t
= 1, . . . , m, and hi : X -» X,
h2(x)
= x, x e X, is an
isomorphism
of
A
onto
.M.
Therefore,
A can be
embedded isomorphically into
M. To
prove that
T
q
(JC)
contains
all
monotone permutation automata,
it
remains
to
show that
P
q
(/C)
contains
an
automaton
jV =
(Af,
X, 5')
having conditions
(la)-(3a).
Consider
the
automaton
A\ in
condition
(1) of our
theorem.
By a\ a
2
and
5i(fli,:c)
7
5i(a2,^),ai,fl2
^
AI,JC
€ X\, it is
clear that
we
have
one of
5i(ai,^)
^
a\ ,
81
(02,
x) ^ 02.
Thus
we
obtain conditions
(1) and (2) of
Lemma 6.18.
(In
particular,
we
also
obtain condition (2a)
of
Lemma 6.18. Naturally, conditions (2a)
and
(3a)
of
Lemma
6.18
do not
hold.)
To
obtain
all
required properties
of
A/",
we
consider
B\,...,
B^m
^ N
defined
in
Lemma 6.18 with
s = m + 1.
Thus
all
requirements
(la)-(3a)
hold occurring
in
the
proof
of our
theorem.
(It is
clear that
in
this case
we get for
every
t e {1, . . . , m} and
yi, y
2
€ X,
8(b
t
,
yO =
8(b
t
,
y
2
~)
^
b
t
.)
Theorems 6.22, 6.23,
and
6.24 completely characterize
all
classes r
ao
(/C)
(=
whenever
/C is a
class
of
autonomous automata. Indeed,
if
/C
does
not
satisfy
condition
(1)
of
Theorem 6.24 and, simultaneously,
it
contains
a
nontrivial automaton, then
we can
apply
Theorem 6.23.
If
either
K, is a
class
of
trivial automata
or K,
does
not
satisfy
condition
(2)
of
Theorem 6.24,
we can
apply Theorem 6.22.
Theorem
6.25.
If
K, is a
class
of
permutation automata
containing
a
nonautonomous
permutation
automaton, then
T
ao
(1Q
=
T
q
()C)
is the
class
of
all
permutation automata.
Proof.
Let A = (A, X, 8) be an
arbitrary permutation automaton
and
let,
for
every
x e X,
M
x
= (M,
{x
0
,
x},
8
X
)
be as
before, where
x
0
^ x is an
arbitrary symbol,
A c M , and

6.4.
Temporal
Products
195
moreover,
for
every
b e A,
x
(b,
XQ)
= b and
x
(b,
x) =
8(b, jc).
By
Lemma 6.17,
it is
enough
to
show that
for an
appropriately chosen
A/"
e
T
q
(K),
we get M
x
e
SP
t
I({Af}),
x
eX.
Consider
a
list
a\,
...,a
m
of
the
elements
of A and let M = (N, X,
8')
be an
automaton
with
the
following
properties.
For any
distinct
pair
x, y e X
there exist pairwise disjoint
sets
#1,...,
B
2m
c N
having
(la) \B
t
\
=
\B
m+t
\=3,t
=
l,...,m;
(2a)
for an
appropriate
b
t
e B
t
, B
t
=
{b
t
, 8'(b
t
,
x),
8'(b
t
, y)},
t =
1,...,
m;
(3a)
B
m+t
=
{b
m+t
,
b
l
m+t
,
b
2
m+t
}, where '(b
l
m+t
,
x) =
8'(b
2
m+t
,
y) =
b
m+t
,
t =
l,...,m.
Take
the
bijective mapping
h : N -» N
such that
for
every
t E
{1,...,
m},
h(b
m+t
)
=
bt,
h(bm+1
t
)
=
8'(b
t
,
y) and for
every
x e X,
h(b™+
t
)
=
S'(b
t
,x\
whenever
8(a
t
,x)
=
at,
{1,...,
m}.
Construct again
an
automaton
M' = (N, X, 8")
which
is
isomorphic
to N and
"(h(b'),
x) =
h(8'(b',
x)),
bzN,xeX.
Let x
0
be an
arbitrary symbol. Construct
the
temporal product
M = (N,
{XQ,
x},
8
X
)
=
NxJ\f'({xo,
x},
(p)
suchthat^(^r)
=
(jc,
y),
<P(XQ)
= (y, x).
Suppose that
8
A
(a
t
,
x) =
a
t
, a
t
e
Aholdsforana,
e A.
Thus
we get
^(fc,,*)
=
8"(8'(b
t
,x),
y) =
8"(h(b
(
^
+i
),
y) =
h(8'(b™
+t
,
y» =
h(b
m+
A=bt.
Similarly,
8
x
(b
t
,
x
0
) =
"(8'(b
t
, y),*)
=
8"(h(b
(
^
+t
),
x) =
h(8'(b
(
V
+t
,x»
=
h(b
m+t
)
= b
t
.
Therefore,
<7ii,/i
2
)
with
^ : A -» N,
hi(a
t
)
=
b
t
,t
=
1,...,
m, and h
2
: X -> X,
h
2
(xo)
=
XQ,
h2(x)
= x is an
isomorphism
of A
x
onto
M
x
.
Therefore,
A can be
embedded isomorphically into
M.. We now
show
N € T
q
(1C).
Let = (D,
Xx>, 5x>)
be any
nonautonomous permutation automaton
from
AC.
It can
be
seen easily that
T>
has the
following properties:
(Ib)
For a
triplet
a e A, x, y e
X-D, &v(d,
x) ^
8
D
)(d,
y).
(2b) There
are
distinct states
d
1,
d
2
and distinct inputs
x, y €
-Xp
such that
8
D
(d1,x)
=
8v(d2,
y).
(3b) There exists
a
triplet
d\, d
2
€ D, x e X
having p(^i,
x)
8-D(d
2
,
x).
(4b) There
are d G D, x G X
with 8v(d,
x) d.
By
conditions
(lb)-(4b)
we
obtain
as
follows. Using Lemma 6.18,
for any
distinct
pair
x, y € X
there
can be
constructed
a
quasi-direct power
of V
having
the
conditions
(la)-(3a)
given above.
In
detail,
by
Lemma 6.18
we can get b
t
{8'(b
t
,
x),
8'(b
t
,
y)} and
b
m+t
i
{b
r
£_
t
,
bS{
t
],
with &J!i,
^
b%>
+t
,
t =
1,...,
m. By
(2b),
we
may
obtain 8'(b
t
,
x)
8'(b
t
,
y).
Finally,
the
disjunctivity
of
B\,...,
B^
comes
from
Lemma 6.18. This ends
the
proof.
Of
course,
for
every nonmonotone reset automaton
A, the
two-state reset automaton
can
be
embedded isomorphically into
A.
Therefore, using Proposition 3.14, every reset
automaton
can be
embedded isomorphically into
a
quasi-direct power
of A as
long
as A is
a
nonmonotone reset automaton. Thus,
by
Theorem 6.16,
we
have
the
following.
Theorem 6.26.
If
1C
is a
class
of
reset
automata
containing
a
nonmonotone
reset
automaton,
then
T
q
(lC)
is the
class
of
all
reset automata
and
T(/C)
is the
class
of
all
automata.

196
Chapter
6.
Primitive
Products
and
Temporal
Products
Observe that Theorems
6.22-6.26
inform
us
about
the
structure
of T
ao
(/C)
and T
q
(/C)
whenever
K, is a
class
of
either autonomous automata, permutation automata,
or
reset
automata. Otherwise,
we can use
Theorem 6.19. This
is
summarized
in the
next statement.
Corollary 6.27.
For
every
class
of
automata,
T
aQ
T
(1C)
= T
(JC).
Moreover,
T
()C)
=
T
q
(lC),
whenever
1C
consists
of
autonomous
automata,
or /C has a
nonreset automaton.
In
particular,
ifK.
is a finite
class
of
automata, then
for an
arbitrary
automaton
A it can be
decided
whether
or not A e
T
ao
(/C)
or A e T
q
(K).
Now we
shall study
the
T
g
-product.
Lemma 6.28.
If
1C
is a
class
of
autonomous automata, then
T
g
(lC}
=
T
q
(lC).
The
following statement characterizes
all
complete
classes
with
respect
to
isomorphic
representations under
the
T
g
-product.
Theorem
6.29.
Any
class
/C
of
automata
is
complete with
respect
to
isomorphic
represen-
tations
under
the
T
g
-product
if
and
only
if)C
contains
a
nonautonomous automaton.
Proof.
Every quasi-direct product
is an
ao-product. Moreover, every ao-product
is a
general
product. Thus because
of
Lemma 6.28
and
Theorem 6.16
we
obtain
the
necessity
of our
condition.
To
establish
the
sufficiency,
let A = (A, X, ) €
1C
be a
nonautonomous automaton
with
a
suitable
triplets
€ A, x, y e X
satisfying
(a, x)
8(a,
y).
Observe that
K
satisfies
condition
(1) of
Theorem 6.19.
By
Theorem 6.20,
it is
enough
to
show that
for
suitable
single-factor
products
AI, A
3
of A,
conditions
(2) and (3) of
Theorem 6.19 also hold.
We
prove this
fact
as
follows:
(la) There exist
a\, 02 € A, x, y e X
with
a\ a
2
and
(a\,x)
=
8(a
2
,
y).
(2a)
There
are a
1
, a^ e A, x e X
holding
a\ ^
a-i
and
8(a\,x)
^
8(02,
y).
If
A is not a
permutation automaton, then
(by x = y) we
have (la), obviously.
Therefore,
to
establish
la) it is
enough
to
take
the
case that
A is a
permutation automaton.
Then
we
have
a
triplet
a e A, x, y € X
with 8(a,
x) ^
8(a,
y).
Thus there
are a
pair
a(
(=
8(a, x)),
a'
2
(=
8(a,
y))
from
A and
positive integers
k, I
such that
a{ a'
2
and
8(a{,
x
k
) =
8(a
f
2
,
y
1
) (= a). By an
easy computation
we
obtain that (la) also holds.
Suppose that
any
permutation automaton
B is
trivial
if B is a
subautomaton
of A.
Then
by our
assumptions,
A has a
nonautonomous definite subautomaton
A. If A is
not
a
reset automaton, then
we
obtain (2a)
by
definition.
If A is a
nonautonomous reset
automaton,
then there
are a, b e A,
jc,
y e X
with
a b and
8(a,
x) = a,
8(b,
y) = b.
Hence
we get
(2a).
Now
let us
assume that
A has a
subautomaton that
is a
nontrivial permutation
au-
tomaton. Then
for a
suitable pair
b e A, z € X
there
is a
positive integer
k > 1
holding
8(b,
z
k
) = b and
8(b,
z
1
} b if t
does
not
divide
k.
Then (2a) holds whenever
a
1
= b, a
2
=
8(b,
z
k-1
),
and x = y = z.
Indeed, since
a\ a
2
,
(a
1
,x)
=
8(b,
x),
8(a
2
,
x) = b, and
(b,
x) ^ b,
respectively,
we get
(2a).
In
the
proof
of
Theorem 6.29
we
also proved
the
following statement.

6.5.
Bibliographical
Remarks
197
Theorem
6.30.
If
any
class
K,
of
automata
is
complete
with
respect
to
isomorphic
represen-
tations
under
the
T
g
-product,
then
it is
complete
with
respect
to
isomorphic
representations
under
the
T
q
t-product.
It
is
clear that
the
class
of all
autonomous automata
is
closed under homomorphisms.
Therefore, using Lemma 6.28,
we
have
the
following.
Theorem 6.31.
Any
class
)K of
automata
is
complete
with
respect
to
isomorphic
repre-
sentations
under
the
T
g
-product
if
and
only
if
K, is
complete
with
respect
to
homomorphic
representations
under
the
T
ql
-product.
As
a
consequence
of
Lemma 6.28, moreover,
via
Theorems
6.29-6.31,
respectively,
we
obtain that
the
T
g
-product
is
equivalent with
the
T
q
t
-product
from the
point
of
view
of
isomorphic
and
homomorphic representation. Thus
our
statements also hold whenever
for
any
i > 0 we
consider either
T
Ui
-products,
or
T
Vl
-products
or
Tprimitive
-products instead
of
T
g
-products. Thus
we
have obtained
the
next result.
Theorem
6.32.
For
every
positive
integer
i the
T
g
-product
is
equivalent
to the
T
Ui
-product
and
also
to the
T
Vi
-product
from the
points
of
view
of
both
homomorphic
or
isomorphic
representations.
Similarly,
the
T
g
-product
is
equivalent
to the
Tp
rimitive
-product
from the
points
of
view
of
both
homomorphic
or
isomorphic
representations.
Note that using Lemma 6.28
for any
class
K, of
autonomous automata Theorems
6.22-6.25
gives information about
the
structure
of
T
g
()C)
=
T
q
e(K.).
Moreover,
if /C has a
nonautonomous automaton, then
T
g
(JC)
=
T
q
t(JC)
is
characterized
by
Theorem 6.31.
By
these
facts,
we
obtain
the
following statement.
Corollary 6.33.
For any
class
1C
of
automata,
T
g
T
g
(JQ
=
7^(/C).
In
particular,
ifK,
is
a finite
class
of
automata,
then
for an
arbitrary
automaton
A it is
decidable
whether
.4 e
r.(/Q(=
7X/Q).
D
6.5
Bibliographical
Remarks
Section
6.1. Basic properties
of
primitive products were described
by P.
Domosi
and
C.
L.
Nehaniv
[2000].
Section
6.2. Connections
of
primitive products
and
Letichevsky's criterion were also shown
by
P.
Domosi
and C. L.
Nehaniv
[2000],
Section
6.3.
By
Letichevsky's
result
[1961],
a
class
of finite
automata
is
complete with
respect
to
homomorphic representations under
the
GluSkov
product
if and
only
if it
satisfies
Letichevsky's criterion. Theorem 6.15
is the
main result
hi P.
Domosi
and C. L.
Nehaniv
[2000]
showing
the
same
fact
for the
primitive product.
Section
6.4. Temporal products were introduced
by G. I.
Ivanov
[1973].
An
abstract
model
of
multichannel
finite-state
machines
was
introduced
by A.
Gill
[1970].
Temporal
compositions
of
a,-products were introduced
by F.
Gecseg
[1976a].
They were also studied
by
P.
Domosi
[1986].
All
results
of
this section
are from P.
Domosi
[1988].
This page intentionally left blank

Chapter
7
Finite
State-Homogeneous
Automata
Networks
and
Asynchronous
Automata
Networks
Computer network routing, communication,
and
computation problems involving identical
(or
different)
component processors connected according
to a
graph
D
with synchronous
update
are in
fact
just
automata network problems.
The
interconnection digraph
D,
which
we
call
the
underlying digraph
of the
network,
is
often
referred
to in the
literature
as the
topology
of the
network.
State-homogeneous automata networks
are
those that have
the
same
set Z
of
states
at
every node
of D.
They
are
natural generalizations
of
the
concept
of
cellular automata,
but
many receive external inputs
and
have
different
local automata.
The
n-completeness
of
a
homogeneous
finite
automata network means that
it is
able
to
simulate
a
complete homogeneous
finite
network
in a
very strong sense.
The
main results
of
Sections
7.1-7.4
(similar
to the
results
of
Chapter
2)
show that
the
homogeneous automata
networks (having
all
loop edges)
are
very
stable: removing many links,
the
network with
n 1
nodes remains n-complete
as
long
as it
remains strongly connected
and has a
central
element.
If
the
network
has
more than
n
nodes, then strong connectivity
is
enough
for n-
completeness (i.e.,
a
central element
is not
necessary
in
this case). These results
are in
accordance
with
the
well-known experimental results that many real-world networks
are
very
stable against removing several links.
We
also show
in
this chapter
a new
method
for the
emulation
of the
behavior
of
any
(synchronous) automata network
by a
corresponding asynchronous
one
which
is
obtained
by a
simple construction over very similar digraph (Section 1.5).
In
particular,
most results
for
automata networks
can be
carried over
in a
wholesale fashion
to the
asynchronous realm. Special cases
of
this result show
how
synchronous generalized cellular
automata (automata networks with
only
one
input symbol,
a
clock
tick)
and
synchronous
cellular automata (which,
in
addition,
are
state-homogeneous)
can
also
be
emulated
by
the
corresponding
type
of
asynchronous network.
The
results
of
this section also hold
for
automata networks over locally
finite
digraphs.
So, for
example, asynchronous universal
cellular automata
can be
constructed from synchronous ones.
199

200
Chapter
7.
Finite State-Homogeneous
and
Asynchronous
Automata Networks
7.1
State-Homogeneous Networks
and
Some
Technical
Lemmas
From
now to
Section 7.5,
let us
consider state-homogeneous automata networks, that
is,
automata networks
in
which each local component automaton
has the
same state
set Z.
We
shall recover, with
a new
proof,
an
important result concerning completeness under
projection
for
such networks,
as
well
as an
extension
in
Section 7.3,
and in
Section
7.4
further
results
on
minimality
of
networks that
are
complete
in
this sense.
Here
we
recall
the
definition
of
automata network
for the
special case
of
state-
homogeneity: Given
an
automaton
A =
(A,X,8),
let A = Z
n
for
some
|Z| 1 and
n
> 1
(where
|Z|
denotes
the
cardinality, i.e.,
the
number
of
elements
in Z).
Then
we say
that
A is a finite
state-homogeneous automata network
(of
size
n
with
respect
to the
basic
local
state
set Z).
Then
the
underlying
digraph
D
A
= (
VA,
EA) of A is
defined
by VA =
{1,...,
n}, EA =
{(i,
j) I
there exists
x e X
such that
cpj(8
x
)
really depends
on its ith
variable).
A is a
T>-network
if D — (V, E) is a
digraph with
V = V
A
and E E
A
-
In
other words,
A is a
"P-network
if
every mapping
8
X
: A -»• A (x e X) is
compatible
with
Z>.
Note that
a
size-n automata network
may be
regarded
as
comprising
n
component
automata
At = (Z, Z" x X,
,•),
/
{1,...,
n},
where
the 5, are
defined
by
forz
=
(zi,...,
Zn)
€
Z
n
,x
e X. One may of
course notationally suppress
the
components
of
Z" in the
inputs
to AI
upon which
5,
does
not
really depend.
If
n = 1 or |Z| = 1,
then
we say
that
A =
(Z
n
,
X, 8) is a
trivial
(finite)
automata
network.
In
this section
we
will investigate
the
state-homogeneous automata networks
having
state sets
of the
form
Z" for a
positive integer
n > 1 and finite set Z of
cardinality
at
least two. Therefore,
by an
automata network
we
shall mean
a
nontrivial
finite
state-
homogeneous automata network.
We
shall derive
a
sequence
of
technical results
on
self-maps
of
powers
G
n
of a
group
G. In
later
sections,
we
will regard
G as the
local
state
set in an
state-homogeneous
automata
network.
We
start with
the
following result, which
can be
shown
by
elementary
computation.
Lemma
7.1. Given
a finite
group
G and a
positive
integer
n > I, let us
define
for
every
distinct
i, j e
{1,...,
n}
the
Junctions
F(
t)
: G
n
-+ G", t = 1, 2, 3,
FJ
4)
: G
n
-> G", and
Uij
: G
n
-> G
n
as
follows:
