Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry
Подождите немного. Документ загружается.

SECTION 8.5 DIRECTIONAL DIFFERENTIATION 229
To get a better feeling for the geometry of (8.10) in 3-D, introduce the unit rotational axis
of the mirror motion m = I
∗
, normalize n to unity, and express the result as a rotational
axis b = B
∗
. Some manipulation gives
b = 2 n(n ∧ m) = 2 (m ∧ n)/n.
This axis is the rejection of m by n, or (if you prefer) the projection of the axis m onto the
plane with normal vector n. That projection obtains a factor sin ψ of the angle ψ between
n and m. The rotation angle β for the reflection
n[X] of X under the rotation of around
the m axis is the norm of b, which evaluates as
β = 2 sin(ψ).
(8.11)
This is a rather powerful result acquired with fairly little effort, only at the very last
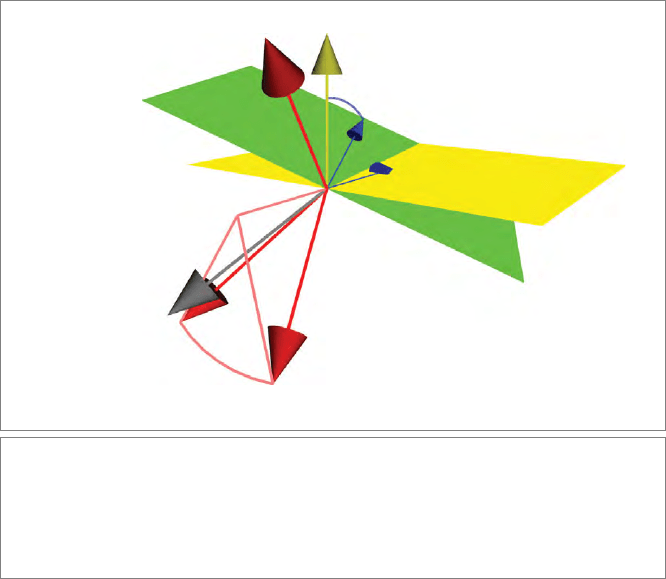
moment requiring some trivial trigonometry. Figure 8.2 sketches the situation. Two
b 5 2φ(m ∧n)/n
mφ
2
φ sinψ
1
st
order R[n[x]]
true R[n[x]]
n
x
−nxn
−1
ψ
Figure8.2: Changes in reflection of a rotating mirror. The yellow mirror with normal n rotates
around the m axis over an angle
, producing the green mirror plane. This changes the reflec-
tion −nxn
−1
of a vector x to the gray vector. That change is to first order described as the
rotation of −nxn
−1
around an axis that is the projection of m on the n plane, over an angle
2
sin ψ, where ψ is the angle between n and m. This involved and geometrically quantitative
figure is the result of only a few lines of coordinate-free computation in geometric algebra.

230 GEOMETRIC DIFFERENTIATION CHAPTER 8
special cases make perfect sense: if ψ = 0, then n and m are aligned, and indeed no
rotation over m changes the reflection of X; and if ψ = π/2, then n and m are per-
pendicular, and any rotation of the rotation plane becomes a 2 rotation of the
reflection
n[X].
We will get back to this rotated reflection in its full generalit y in Section 13.7.
8.6 VECTOR DIFFERENTIATION
In scalar differentiation, we consider a vector function as a changing in time (or some
such scalar parameter). We may also want to consider F(x) as a function of position as
encoded by the vector variable x, and differentiate directly relative to that variable. This
is most easily defined by developing it on a basis, doing a directional differentiation with
respect to each of the components, and reassembling the result in one quantity. It is the
∇-operator of vector analysis, but we wi ll denote it as
∂
x
. This explicitly specifies the vari-
able relative to which we differentiate and prepares for a generalization beyond vectors
and toward differential geometry. On a basis {e
i
}
m
i=1
for the space R
m
in which x resides,
let x
i
denote the coordinate functions of the vector x so that it can be written as
x =
m
i+1
x
i
e
i
.
We will be setting up this vector differentiation in a very general framework, in which
the space
R
m
of x may reside on a manifold (curved subspace) within a larger space R
n
(for instance, x may lie on a 2-D surface in 3-D space). The basis for R
m
may then not be
orthonormal, so we use the reciprocal basis of Section 3.8, and compute x
i
as x
i
= e
i
· x.
The directional derivative in the coordinate direction of e
i
is simply the scalar derivative
of the coordinate function:
(e
i
∗ ∂
x
) =
∂
∂x
i
= ∂
x
i
.
As their notation suggests, we can assemble the results of each of these directional oper-
ators and consider them as the components of a more general vector derivative operation
defined on this basis as
∂
x
≡
m
i=1
e
i
(e
i
∗ ∂
x
) =
i
e
i
∂
∂x
i
.
(8.12)
(When you study reciprocal frames, expressions like these are actually coordinate-free
when they contain the upper and lower indices that cancel; in physics, lower-index vectors
are called covariant and upper-index vectors contravariant, but we will not follow that
terminology here.)
The operator
∂
x
computes the total change in its argument when x changes in all possible
ways, but it keeps track of those changes in a geometrical manner, registering the e
i
-related
SECTION 8.6 VECTOR DIFFERENTIATION 231
scalar change in the magnitude of the e
i
component of the total change. Preserving this
geometrical information is surprisingly powerful, and in advanced geometric calculus it
is shown that this operator can be inverted by integration (see [26]).
You should interpret the grade of the operator
∂
x
as a vector (i.e., as the grade of its sub-
script). As a geometrical vector operator, it should conform to the commutation rules for
geometric products. We will not use the square application brackets here, for it is more
productive to see this as a geometric element rather than as a linear operator, and to move
it to other places in the sequence of symbols for computational purposes. The subscript
x in
∂
x
denotes which vector variable is being differentiated (and this is necessary when
there is more than one).
As an example, we apply the vector differentiation to the function F(x) = x
2
, rela-
tive to its vector parameter x:
∂
x
x
2
=
i
e
i
∂
x
i
j, k
x
j
x
k
e
j
· e
k
(coordinate definition)
=
i
e
i
k
x
k
e
i
· e
k
+
j
x
j
e
j
· e
i
(coordinate independence)
= 2
i
e
i
(e
i
· x) (linearity)
= 2 x .
(8.13)
We obtain the result 2x, which you might have expected from pattern matching
with scalar differentiation (though that is a dangerous pr inciple to apply). The
result is not a vector, but a vector field that has the value 2x at a location x.
This vector field is in fact the gradient of the scalar function x
2
(i.e., the
direction in which it var ies most, with a magnitude that indicates the amount
of variation).
The recognition of the multiplication in
∂
x
F(x) as the geometric product makes it quite
natural to expand this in terms of the inner and outer product, simply applying (6.14):
∂
x
F(x) = ∂
x
F(x) + ∂
x
∧ F(x).
For a vector-valued function F, the first term corresponds to the usual divergence
operator div[F(x)] ≡∇·F(x), and the second term is related to the curl operator
rot[F(x)] ≡∇×F(x), written in terms of the 3-D cross product; it is actually its dual.
As with the other uses of the cross product, replacing the curl by an outer-product-
based construction ensures validity in arbitrary dimensionality. If F is scalar-valued,
then only the
∂
x
∧ F(x) term remains, and is identical to the gradient operator
grad[F(x)] = ∇F (x). For a symmetric vector function F
+
(equal to its adjoint), the
part
∂
x
∧ F
+
[x] equals zero, for a skew-symmetric vector function F
−
(opposite to
its adjoint), the part
∂
x
· F
−
[x] equals zero.

232 GEOMETRIC DIFFERENTIATION CHAPTER 8
8.6.1 ELEMENTARY RESULTS OF VECTOR DIFFERENTIATION
We have introduced the vector differentiation as the geometric algebra equivalent of
the ∇-operator from vector analysis. Although the definition as we have given it uses
coordinates, the vector differentiation is a proper geometrical operation that is not
dependent on any chosen coordinate system. When you apply it, you should avoid
coordinates, and instead use results from a table of standard functions (combined
with product rule and chain rule of differentiation). We give such a collection of
useful elementary results in Table 8.1, and derive some of its more educational entries
below.
•
Identity Function x. The identity function F(x) = x has a derivative that depends
on the dimensionality of the space
R
m
in which x resides.
∂
x
x =
i
e
i
∂
∂x
i
[
j
x
j
e
j
]
=
i,j
δ
j
i
e
i
e
j
=
i
e
i
e
i
=
i
e
i
· e
i
+
i
e
i
∧ e
i
=
i
1 + 0 = m.
(Here we used
i
e
i
∧ e
i
= 0, given as (3.35).) This algebraic derivation gives
a clue for the correct geometrical way to look at this: all changes in all direc-
tions are to be taken into account. In m-dimensional space, there are m directions,
and each of these provide a unit change in coordinates with each unit step, for a
total of m.
Since the vector differentiation applies as a geometric product, you can split the
result in an inner and outer product part that the computation above has shown to
obey
∂
x
·x = m and ∂
x
∧x = 0. The outer product result ∂
x
∧x = 0 shows that you
can think of
∂
x
as being like a vector in the x direction, and the inner product result
then shows that it is like m/x (but view these as no more than mnemonics;
∂
x
is of
course not a vector but an operator).
•
Inner Product x ·a. When we study the change in the scalar quantity F(x) = x · a
(geometrically the projected component of x ontoavectora
−1
), we should in gen-
eral allow for the variations of x to be in its m-dimensional manifold (curved sub-
space), whereas a may be a vector of the encompassing space
R
n
(for instance, x on
a sphere, a a general vector in 3-D space; x · a is well defined everywhere on the
sphere, so it has a derivative).
Two things happen to the measured changes caused by variations in x. First, even
when x and a are in the same m-dimensional space, the quantity x·a can only pick up
the changes in the direction a, so summing over all directions only this 1-D variation
remains. Second, x cannot really vary in the a-direction, since it has to remain in its

SECTION 8.6 VECTOR DIFFERENTIATION 233
m-dimensional manifold, or more accurately, in the tangent space at x isomorphic
to
R
m
, for which {e
i
}
m
i=1
is the basis. It is the projection of the a-direction onto this
tangent space that must be the actual g radient.
The algebraic computation confirms this, with indices i and j ranging over
coordinates for the space in which x resides, and k over the space of a, using a
local coordinate basis for the total n-dimensional space in which the problem is
defined:
∂
x
(x · a) =
i
e
i
∂
∂x
i
[
j
k
x
j
a
k
e
j
· e
k
]
=
i
k
a
k
e
i
(e
i
· e
k
)
=
i
a
i
e
i
= P
I
m
[a],
since the summation of the a components is only done for the elements in the
basis of the tangent space at x with pseudoscalar I
m
. In tables, we will use P[a] as
shorthand.
•
Outer Product x ∧a. When we compute the variation of the bivector x ∧ a, this can
be rewritten as the variation of xa − x · a. The variation over x in the first term
causes a factor m (the dimensionality of the space that x resides in), but of course it
picks up only the part P[a] of a. The second term we have seen above, and the total
variation is now
∂
x
(x ∧ a) = (m − 1) P[a].
•
Norm x. Geometrically, what would you expect the derivative of the norm to be?
Since it is a scalar function, the vector derivative will be the gradient of the norm, i.e.,
the direction in which it increases most steeply weighted by the weight of increase.
So the answer should be x /x, the unit vector in the x direction. The algebraic
computation confirms that it is:
∂
x
x =
i
e
i
∂
x
i
j,k
x
j
x
k
e
j
· e
k
1/2
=
i
e
i
(
k
x
k
e
i
· e
k
+
j
x
j
e
j
· e
i
)/(2x)
=
i
e
i
(e
i
· x)/x
= x /x.
This result depends on the metric through the norm x.
•
Adjoint as Derivative. When we introduced the adjoint f of a function f in Sec-
tion 4.3.2, we only had an implicit definition through x ∗f[y] =
f[x] ∗ y. Using the
vector derivative, we can define the adjoint explicitly as

234 GEOMETRIC DIFFERENTIATION CHAPTER 8
f[x] ≡ ∂
y
(f[y] ∗ x), (8.14)
where both x and y are in the same space
R
m
(to avoid the need for a projection).
You can prove it immediately by rewriting the argument of the differentiation using
the earlier definition. This definition can also be applied to nonlinear functions, and
it then computes a local adjoint, which may be different at every location x.
8.6.2 PROPERTIES OF VECTOR DIFFERENTIATION
The vector differentiation operator is clearly linear. It also obeys a product rule, though we
need to take care of its noncommutativity. Therefore, it becomes inconvenient to denote
its application by square brackets; we need a more specific notation. Dropping the refer-
ence to x for readability, we express the product rule as
∂ (FG) =
`
∂
`
FG+
`
∂ F
`
G,
where in each term the accent denotes on what factor the scalar differentiation part of
the
∂ should should act—the geometric vector par t is not allowed to roam, so we cannot
simply say that the operator acts on the element just to the right of it. To give an example:
∂
x
(xx) =
`
∂
x
`
xx+
`
∂
x
x
`
x =
`
∂
x
`
xx+
`
∂
x
(2(
`
x · x) −
`
xx) = 2
`
∂
x
(
`
x · x) = 2x.
Note that the subtle swap to get the elements into standard order precisely kills the term
`
∂
x
`
xx= m x.
Because of the noncommutativity, there are other product rules, such as
F
∂ G =
`
F
`
∂ G + F
`
∂
`
G,
with the accents again denoting how to match each differentiation with its argument.
There is also a chain rule, which looks a bit complicated. Let the coordinate x be hidden
by a vector-valued function y, so that the dependence of F on x is F(y(x)). Then the chain
rule of vector differentiation is
∂
x
F(y(x)) =
`
∂
x
y(
`
x) ∗
∂
y
F(y).
The two geometric products in this equation can be executed in either order due to
associativity. If we start from the right, this states that we should first consider F as a
function of y and do a directional differentiation in the y(x)-direction; that typically
gives something involving both y(x) and y. We should not substitute x in the latter, but
differentiate the x-dependence in the former. This can be confusing, so let us do an
example.
Let G(y) = y
2
, and y(x) = (x ·a) b. If we would just evaluate G as a function of x by
substitution, we would get G(x) = (x · a)
2
b
2
, so that ∂
x
G(x) = 2(x · a) ab
2
.The
chain rule application should produce the same answer.

SECTION 8.7 MULTIVECTOR DIFFERENTIATION 235
We first evaluate from the right, so we start with the directional differentiation
of G(y) = y
2
. For a general vector z, the directional derivative (z ∗ ∂
y
) y
2
= 2 z · y,
so with z = y(x) the result is 2 y(x) ·y = 2(x · a)(b ·y). Note that we kept y.Inthe
second step, this expression needs to be differentiated to x, giving
∂
x
2(x · a)(b ·
y)
= 2 a (b · y). That is the answer, but we prefer it in terms of x, so we should
substitute the expression for y in terms of x, giving the same result as before.
If instead we had evaluated from the left, we would first need to evaluate
`
∂
x
y(
`
x) ∗
∂
y
=
∂
x
(x ·a) b
∗
∂
y
= a (b ∗∂
y
). Do not be bothered by the presence
of
∂
y
in this derivation; since it is not differentiating anything, it behaves just like
a vector. Now we apply the resulting operator to G(y) = y
2
, giving 2 a (b · y) as in
the other evaluation order. Here, too, you would need to substitute the expression
y(x) to get the result in terms of x.
The operator we just evaluated can be rewritten using the definition of the
adjoint of the function y(x) = (x · a) b,whichis
y(x) = (x · b) a.Wethenrec-
ognize a (b ∗
∂
y
) as the adjoint of the y-function applied on ∂
y
, i.e.,
y[∂
y
].Wecan
also use the adjoint to write the actual answer for our differentiation of the squar-
ing function G as 2
y(y(x )), which actually holds for any function y usedtowrap
the argument x.
The implicit understanding of how to deal with the substitutions in the equation is a bit
cumbersome. A more proper notation for the process may be to keep the x in there at all
steps:
∂
x
G(y(x)) =
`
∂
x
y(
`
x) ∗
∂
y(x)
G(y(x)) =
y[∂
y(x)
] G(y(x)). (8.15)
The final rewriting uses the differential definition of the adjoint of (8.14) (which also
holds for nonlinear vector functions y). This usage was motivated in the example. It
means that we treat the differentiation operator
∂
y(x)
just as the vector it essentially is.
Then the differentiation with respect to y(x) should be understood as above, but the
lack of an accent denotes that that particular x-dependence should not be differentiated
by
`
∂
x
.
So in the end, the chain rule is essentially a transformation of the differentiation opera-
tor: when an argument gets wrapped into a function, the differentiation with respect to that
argument gets wrapped into the adjoint of that function.
8.7 MULTIVECTOR DIFFERENTIATION
We can extend these forms of differentiation beyond vectors to general multivectors,
though for geometric algebra, the extension to differentiation with respect to blades and
versors is most useful. Another extension is the differentiation with respect to a linear
function of multivectors, which finds uses in optimization. We will not treat that here,
but refer to Chapter 11 in [15].

236 GEOMETRIC DIFFERENTIATION CHAPTER 8
8.7.1 DEFINITION
The definition of directional multivector differentiation is a straightforward extension of
the idea behind the directional vector differentiation. You simply vary the argument X of
a function additively in its A-component, so that A should at least be of the same grade as
X (as for instance when X is perturbed by a transformation, to first order). The definition
reflects this grade-matching in its use of the scalar product:
(A ∗
∂
X
) F(X) ≡ lim
→0
F(X + A) − F(X)
.
We emphasize that this is a scalar operator, since the grade of the result is the same as that
of the original function.
As in the case of the vector derivative, we can see the directional multivector derivative
as merely one component of a more general multivector derivative. We introduce coordi-
nates now for the total 2
m
-dimensional space of multivectors in the tangent space R
m
at
X. To distinguish it clearly from the m-dimensional vector basis, let us denote this mul-
tivector basis by a running capital index: {e
I
}
2
m
I=1
. As w ith the vector basis in the vector
derivative, this may not be orthonormal, so we also employ a reciprocal basis {e
I
}
2
m
I=1
;see
also Section 3.8. Then the multivector derivative is defined as
∂
X
=
I
e
I
(e
I
∗ ∂
X
),
where e
I
in principle runs over all 2
m
elements 1, e
i
, e
i
∧ e
j
, and so on, and the scalar
product selects only the basis elements that are components of X.
This clearly contains vector differentiation as a special case. But also scalar differentiation
is included: if we let X be a scalar X = τ, only the basis element e = 1 is selected, so
∂
τ
= 1(1∗ ∂
τ
) = (1 ∗ ∂
τ
) =
d
dτ
, conforming to our earlier definition of this symbol. For
scalars, directional differentiation and multivector differentiation coincide.
As with the vector derivative, the coordinate-based definition should be used to derive
elementar y coordinate-free results, which should then be the basis of all actual compu-
tations. We have collected some in Table 8.2, including results on scalar functions that
often occur in optimization problems. The pattern of derivation of these equations is
completely analogous to that for vector differentiation.
8.7.2 APPLICATION: ESTIMATING ROTORS OPTIMALLY
This example is taken from [36]. We are given k labeled vectors u
i
, which have been rotated
to become k correspondingly labeled vectors v
i
. We want to t ry and retrieve that rotor
from this data. If both sets of vectors are measured with some noise (as they usually are),
we cannot exactly reconstruct the rotor R, but we have to estimate it. Let us use as our
criterion for fit the minimization of the total squared distance between our estimated

SECTION 8.7 MULTIVECTOR DIFFERENTIATION 237
Table 8.2: Elementary results of multivector differentiation. The multivector varies in the
space
R
m
, contained in the larger space
R
n
. The map P[] projects from the latter to the
former.
(A ∗ ∂
X
) X = P[A]
(A ∗ ∂
X
)
X = P[
A]
(A ∗ ∂
X
) X
k
= P[A] X
k−1
+ X P[A] X
k−2
+ ···+ X
k−1
P[A]
∂
X
X = m
∂
X
X
2
= 2
X
∂
X
(X ∗ A) = P[A]
∂
X
(
X ∗ A) = P[
A]
∂
X
(X
−1
∗ A) = P[−X
−1
AX
−1
]
∂
X
X
k
= k X
k−2
X
rotation vectors compared to where we measured them. This is an old problem, known in
biometrics literature as the Procrustes problem and in astronautics as Wahba’s problem.
So we need to find the rotor R that minimizes
Γ(R) =
k
i=1
(v
i
− R u
i
R)
2
=
k
i=1
(v
2
i
+ u
2
i
− 2v
i
R u
i
R
0
).
(8.16)
Preferably, we would like to differentiate this with respect to R and set the resulting
derivative to zero to find the optimal solution. However, the rotor normalization
condition R
R = 1 makes this mathematically somewhat involved. It is easier to
temporarily replace the rotor R byaversorV and consequently to replace
R by V
−1
,

238 GEOMETRIC DIFFERENTIATION CHAPTER 8
and then to differentiate relative to the unconstrained V to compute the optimum
V
∗
. Clearly the terms without R (or V) do not affect the optimum, so
V
∗
= argmax
V
k
i=1
v
i
V u
i
V
−1
0
.
Now we differentiate by
∂
V
and use the product rule. We can use some of the results
from Table 8.2 once we realize that this is differentiation of a scalar product and use its
symmetry and reordering properties (as (6.23)):
∂
V
Γ(V) =
k
i=1
∂
V
v
i
V u
i
V
−1
0
=
k
i=1
`
∂
V
[
`
V ∗ (u
i
V
−1
v
i
)] +
`
∂
V
[(
`
V
−1
) ∗ (v
i
Vu
i
)]
=
k
i=1
u
i
V
−1
v
i
− V
−1
(v
i
Vu
i
) V
−1
= 2 V
−1
k
i=1
(Vu
i
V
−1
) ∧ v
i
.
Therefore the rotor R
∗
that minimizes Γ(R) must be the one that satisfies
k
i=1
(R
∗
u
i
R
∗
) ∧ v
i
= 0.
(8.17)
This algebraic result makes geometric sense. For each v
i
, it ignores the components that
are just scalings of the corresponding rotated u
i
; the rotation cannot affect those parts
anyway. Only the perpendicular components matter, and those should cancel overall if
the rotation is to be optimal—if not, a small extra twist could align the vectors better.
The result so far does not give us the optimal rotor R
∗
explicitly; it has merely restated the
optimization condition in a manner that shows what the essential components of the data
are that determine the solution. Our reference [36] now cleverly uses vector differentiation
to manipulate the equation to a form that can be solved by standard linear algebra. First,
they observe that if we introduce the linear function
f[x] =
k
i=1
u
i
(v
i
· x),
the condition (8.17) can be written as
∂
x
∧ (R
∗
f[x]
R
∗
) =
1
2
k
i−1
∂
x
(v
i
· x)(R
∗
u
i
R
∗
) − (R
∗
u
i
R
∗
)(v
i
· x)∂
x
