Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

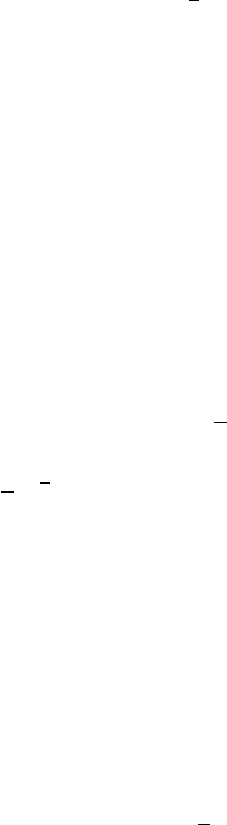
262 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

•

Optimal translation t

given R

, σ

, and the data x

. This involves differentiation

of the cost function relative to t

. The zero derivative is attained at



i=1



− R





(10.16)

This is simply the average difference of where camera j would reconstruct the points

based on its presumed rotations and their true average location.

•

Optimal rotation R

given X

and the data x

. The differentiation with respect to

a rotor was treated in Section 8.7.2 when optimizing (8.16). Here the result corre-

sponding to (8.17) is that the optimal R

must satisfy



i=1



− t

) ∧ (R



)



= 0.

The geometrical interpretation is that the optimal rotor rotates to minimize the

transverse components of all X

when reconstructed by camera j. Substituting the

expression for the optimal t

leads to



i=1



− X

) ∧ (R



)



= 0, (10.17)

where X

≡



k=1

is the centroid of the world points. As in Section 8.7.2, this

optimal R can be found by a singular value decomposition of a linear function

deﬁned in terms of the other parameters.

•

Optimal scaling σ

given R

, t

, and the data x

. This requires scalar differenti-

ation of Γ, and results in

= (X

− t

) · (R

−1



). (10.18)

This is almost a division of the estimated X

by the rotated x

, except that the inner

product makes only the parts along the ray contribute (so that a scalar results).

•

Optimal world points given t

, R

, σ

, and the data x

. Setting the vector derivative

of Γ with respect to X

to zero yields



j=1

+ R



(10.19)

This is simply the average of the estimations of the location of world point i by

each camera.

SECTION 10.5 CONVENIENT ABUSE: LOCATIONS AS DIRECTIONS 263

•

Optimal world points X

given t

, R

, and the data x

.Theoptimumforσ

(10.18) can be substituted in (10.19) to ﬁnd a system of linear equations for X

using R

, t

, and the data x

. That system can be solved optimally by a least squares

technique.

•

Optimal translations t

given R

and the data x

. Another substitution of (10.18)

and combination with the result for the X

leads to a system of homogeneous linear

equations for the t

using an estimate of the R

and the data x

. That system can be

solved optimally using an SVD.

With these composite results, the following iterative scheme can be formulated:

1. Make an initial guess of the R

based on the data using a standard stereo vision algo-

rithm (the geometrical basis for such algorithms will be explained in Section 12.2).

2. Estimate the t

using the estimate of R

and the data x

3. Estimate the world points X

using R

, t

, and the data x

4. Estimate the scaling σ

using (10.18).

5. Obtain a new estimation for R

using (10.17) and iterate from step 2.

The authors of [38] report that a dozen or so iterations are required for convergence

(depending on the number of cameras). The resulting calibration algorithm is fully linear.

In modern calibration practice, it is customary to use the outcome of such linear algo-

rithms as an initial estimate for a few steps of subsequent nonlinear optimization to

improve the estimation.

This algorithm is the basis of the programming example of Section 10.7.3. The com-

pact and direct derivation of the partial solution formulas (10.16) through (10.19) are an

exemplary usage of geometric algebra for these kinds of geometrical optimization prob-

lems in the vector space model.

10.5 CONVENIENT ABUSE: LOCATIONS

AS DIRECTIONS

The vector space model is the natural model to compute with directions and the ultimate

tool for this purpose. It will remain clearly recognizable as a submodel providing the alge-

bra of Euclidean directions, even as we move on to more sophisticated models in the next

chapters.

In a purist point of view, the vector space model would not be used for other tasks. Yet

we can, of course, model location in the vector space model, in the same way as it has

always been done in elementary linear algebra. We just view a location as obtained by

traveling in a certain direction denoted by a direction vector p, over a distance given by

its norm. This treats a direction vector as a position vector, and particularly for problems

264 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

only involving point objects, it is not bad practice. The calibration example of the pre-

vious section shows that it can be very effective, and since that is a problem in which

locations are actually observed as directions, the vector space model is in fact its natural

setting.

When you also have geometrical elements other than pure directions (such as line or

plane offset from the origin), you run into the familiar problems that the use of classical

linear algebra also entailed: translations of such elements require administration of object

types and corresponding data structures. For instance, you can characterize a line by a

position vector and a direction vector, but you should keep them clearly separate, for

under a translation over a vector t, the position needs to change but the direction should

not. Uniformity is only obtained by having a single algebraic element representing the

line, with a representation of translation that can operate on it directly. The vector space

model does not provide that in a structural manner. You need to encode this structure

explicitly or use at least the homogeneous model.

Examples of the “convenient abuse” of directions as locations abound in all graphics

and robotics literature, as well as in typical physics textbooks. Hestenes [29] shows how

geometric algebra can be used effectively in the vector space model to do all of classical

physics. The vector space model does not lack computational power, and its rotors help

considerably in simplifying classical problems like the orbits of planets in a gravitational

ﬁeld (which involve locations, but viewed from the sun so that their directional treatment

becomes natural). But this computational power can only be wielded by manually keeping

track of what geometry is represented by each element and which operations are permit-

ted to be performed on it. That is less a problem for physics (which tends to connect its

equations by natural language anyway), but it is a major source of programming errors in

computer graphics (as reported in [23, 44]). The models of the next chapters will provide

alternatives in which a more extended algebra is used to perform simultaneously both the

computations and the bookkeeping of geometrical elements.

10.6 FURTHER READING

The vector space model may seem prevalent in almost all linear algebra texts, since it is

the most basic way to treat geometry with vectors. However, in geometric algebra, the

full vector space model naturally includes blades and rotors. Not many texts incorporate

those in their treatment of basic geometry.

Your best background material for advanced use of the vector space model of geometric

algebra are texts in introductory physics (such as [29] and [15]). For current use in prac-

tical problems, the papers using geometric algebra in professional journals on computer

vision and robotics are your best source, though these increasingly use the more powerful

conformal model to address problems involving direction and location.

SECTION 10.7 PROGRAMMING EXAMPLES AND EXERCISES 265

10.7 PROGRAMMING EXAMPLES AND EXERCISES

10.7.1 INTERPOLATING ROTATIONS

Interpolating rotations is an important problem with many applications. It is straightfor-

ward to implement once you are able to compute the logarithm of a rotor. This can be

implemented as follows (see Section 10.3.3):

bivector log(const rotor &R) {

// get the bivector/2-blade part of R

bivector B = _bivector(R);

// compute the ’reverse norm’ of the bivector part of R:

mv::Float R2 = _Float(norm_r(B));

// check to avoid divide-by-zero

// (and also below zero due to FP roundoff):

if (R2 <= 0.0){

if (_Float(R) < 0) {

// the user asks for log( — 1)

// we return a 360 degree rotation in an arbitrary plane:

return _bivector((float)M_PI * (e1 ^ e2));

}

else

return bivector(); // return log(1) = 0

}

// return the log:

return _bivector(B * ((float)atan2(R2, _Float(R)) / R2));

}

When you look for this function in the GA sandbox source code package, note that it

resides in the ﬁle

e3ga_util.cpp in the libgasandbox directory and not in the main

source ﬁle of this example. The same is true for the

exp() function listed below. This

exp() is a specialization of the generic exponentiation algorithm, as described in Sec-

tions 7.4 and 21.3.

rotor exp(const bivector &x) {

// compute the square

mv::Float x2 = _Float(x << x);

// x2 must always be <= 0, but round off error can make it

// positive:

if (x2 > 0.0f) x2 = 0.0f;

// compute half angle:

mv::Float ha = sqrt( — x2);

266 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

if (ha == (mv::Float)0.0) return _rotor((mv::Float)1.0);

// return rotor:

return _rotor((mv::Float)cos(ha) +

((mv::Float)sin(ha) / ha) * x);

}

Now that we can go back and forth between rotor and bivector representations of rota-

tions, interpolating rotations becomes straightforward: given two rotors

src and dst,we

ﬁrst compute their difference as the ratio

inverse(src) * dst. Then we compute the

log() of the difference, and scale by the interpolation parameter alpha (which will run

from 0 to 1). The ﬁnal step is reconstructing the rotor using

exp(), and putting it back

in the original frame by multiplying with

src:

rotor interpolateRotor(const rotor &src, const

rotor &dst, mv::Float alpha) {

// return src * exp(alpha * log(inverse(src) * dst));

return _rotor(src * exp(_bivector(alpha *

log(_rotor(inverse(src) * dst)))));

}

The example uses this code to display a rotating/translating frame with a trail following

behind it, as seen in Figure 10.5. Interpolation of translations is done the classical way:

e3ga::vector interpolateVector(

const e3ga::vector &src, const e3ga::vector &dst,

mv::Float alpha) {

return _vector((1.0f — alpha) * src + alpha * dst);

}

Figure 10.5: Interpolation of rotations (Example 1).

SECTION 10.7 PROGRAMMING EXAMPLES AND EXERCISES 267

In later examples—when we gain the additional ability to represent translation and

scalings as rotors—we will redo this example. Only the

log() and exp() functions will

change; the interpolation function remains essentially the same (see Sections 13.10.4 and

16.10.3).

10.7.2 CRYSTALLOGRAPHY IMPLEMENTATION

We have made an implementation to play with the vectors generating symmetries of crys-

tal lattices. An example of the output is Figure 10.6. The application works for the point

groups in 3-D. It shows three input vectors a, b, c drawn as black line segments, which are

the basic generators of the symmetry operators from Section 10.2.3. You can drag those

around to investigate possible nearby symmetries.

The operators are computed from the initial generators in a brute force manner, by repeat-

edly multiplying them with each other to make new versors until no new symmetry oper-

ators are found. To get a true point group, a, b, and c should be chosen in particular ways,

Figure 10.6: Crystallography (Example 2). This example shows the 24 symmetries of a

hexagonal crystal generated from a single red point.

268 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

and for some should be considered as composite operators like (ac). If the generators are

not in the proper conﬁguration to generate a point group, their combination may lead

to an inﬁnite number of versors, but we arbitrarily cut off the generation at 200 different

versors. The largest true point group of cubic symmetry has 48 operators.

To draw the point groups, the code applies the operators to a single (draggable) input

point. A popup menu can be used to initialize the vectors to preprogrammed conﬁgu-

rations (cubic, hexagonal, tetragonal, orthorhombic, triclinic, monoclinic, and trigonal),

corresponding to the seven main point groups. For more details on how to generate all

the subgroups (32 in total), consult [30].

10.7.3 EXTERNAL CAMERA CALIBRATION

This example implements the external calibration of [38], as summarized in Section 10.4.2.

It assumes that the cameras have already been calibrated internally (we used the method

of Zhang [63]), and that we have an initial external calibration (we used the 8-point algo-

rithm, see e.g., [25]).

The data provided with the example is actual calibration data from a geometric-algebra-

based motion capture system built by the authors. The data contains the initial 8-point

calibration estimation, but we have deliberately decreased the quality of the initial esti-

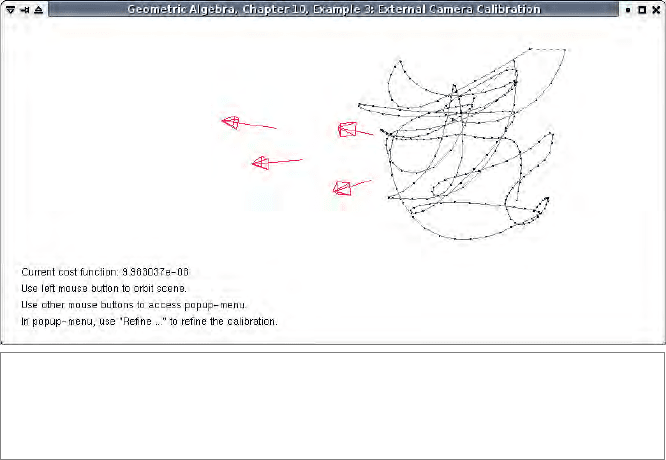
mation to make the effect of the reﬁnement more pronounced. Figure 10.7 shows the

reconstruction of the markers seen by the cameras after completion of the calibration.

Figure 10.7: External camera calibration (Example 3). The cameras are drawn as red wire-

frame pyramids (view volume) with a line indicating their viewing direction. The marker points

used for calibration are drawn as black dots. A line connects the marker points to show how

the single marker was waved through the viewing volume of the cameras.

SECTION 10.7 PROGRAMMING EXAMPLES AND EXERCISES 269

To implement (10.16) through (10.19), we ﬁrst need some context. The data is kept in a

class

State. This state contains cameras in array m_cam, and 3-D world points in array

m_pt:

class State {

public:

// ... (constructors, etc)

// the cameras

std::vector<Camera> m_cam;

// the reconstructed markers, for each frame

std::vector<e3ga::vector> m_pt;

// is reconstruction of markers valid?

std::vector<bool> m_ptValid;

};

The reconstruction of a marker is invalid when it is visible to only one camera.

Each camera carries its own 2-D marker measurements (

m_pt), rotation (m_R and m_Rom),

translation (

m_t), scaling σ

(m_sigma), and per-marker visibility (m_visible).

(We ignored visibility issues when we explained the algorithm, but it is included in [38]

and implemented in the code.)

class Camera {

public:

// ... (constructors, etc)

// rotation

rotor m_R;

// rotation matrix

om m_Rom;

// translation

e3ga::vector m_t;

// for each frame, is a marker visible?

std::vector<bool> m_visible;

// for each frame, the ’2D’ point in the image plane

// (normalized image coordinates, i.e., the e3 coordinate = — 1)

std::vector<e3ga::vector> m_pt;

// for each frame the estimated multiplication factor of m_pt

std::vector<mv::Float> m_sigma;

};

Now each of the equations in Section 10.4.2 can be implemented and those functions

combined in the total algorithm. As an example, (10.16) leads to the code:

270 THE VECTOR SPACE MODEL: THE ALGEBRA OF DIRECTIONS CHAPTER 10

void State::updateTranslation() {

// Iterate over all cameras

// (start at ’1’ because translation of first camera is always 0)

for (unsigned int c = 1; c < m_cam.size(); c++) {

Camera &C = m_cam[c];

vector sum;

int nbVisible = 0;

for (unsigned int i = 0; i < m_pt.size(); i++) {

if ((C.m_visible[i]) && m_ptValid[i]) {

sum += _vector(m_pt[i] - C.m_sigma[i] *

(apply_om(C.m_Rom, C.m_pt[i])));

nbVisible++;

}

C.m_t = sum * (1.0f / (mv::Float)nbVisible);

}

Note that for efﬁciency we use the outermorphism matrix representation of the rotor to

apply it to vectors by means of the function

apply_om(). You can consult the rest of the

code in the GA sandbox source code package.

We will encounter the motion capture system again in Section 12.5.3, when we reconstruct

3-D markers from the raw 2-D data.

THE HOMOGENEOUS

MODEL

While the 3-D vector space model can nicely model directions, it is usually considered

to be inadequate for use in 3-D computer graphics, primar ily because of a desire to treat

points and vectors as different elements that are transformed differently by translations.

Instead, people commonly use an extension of linear algebra known as homogeneous coor-

dinates. This is often described as augmenting a 3-D vector v with coordinates (v

)

to a 4-vector ( v

,1)

. This extension makes nonlinear operations such as translations

implementable as linear mappings.

For the homogeneous model in geometric algebra, the modeling principle is the same: we

embed our n-dimensional base space

(which you may think of as Euclidean R

n,0

,tobe

speciﬁc) in an (n + 1) -dimensional representational vector space

n+1

,ofwhichwethen

use the inherent algebra. That produces a complete algebraic framework, which is well

suited to compute with oriented ﬂats, subspaces offset from the origin in

represented

as blades in

n+1

The algebra of

n+1

provides generally applicable formulas for translation, rotation, and

even afﬁne and projective transformations in the base space

. The operations of meet

and join always return sensible results for incidences of ﬂats. For instance, for two parallel

lines the

meet returns the common direction of the lines as a point at inﬁnity weighted by

their mutual distance. We derive useful covariant and invariant measures, including the

projectively invariant cross ratio, in terms of geometric algebra.

271