Фейгенбаум М. Универсальность в поведении нелинейных систем

Подождите немного. Документ загружается.

1983

г. Октябрь Том

141,

вып. 2

УСПЕХИ

ФИЗИЧЕСКИХ

НАУК

ФИЗИКА

НАШИХ

ДНЕЙ

530.18

УНИВЕРСАЛЬНОСТЬ

ПОВЕДЕНИИ

НЕЛИНЕЙНЫХ

СИСТЕМ*)

Ж.

Фейгепбаум

Хаотизация

поведения

большого

числа

нелинейных

систем

количест-

венно

описывается

универсальными

числами

б =

4,6692016...

и а =

2,502907875...

ОТКРЫТИЕ

Открытие теории универсальности восходит

двум

источникам.

Во-первых,

1971

г.

Н. Метрополис, М.

Стайн

и П.

Стайн

(теоретический

отдел Лос-Аламосской лаборатории) открыли любопытное свойство ите-

раций:

при изменении параметра характер поведения итераций изменяется

способом, не зависящим от конкретного вида итерируемой функции. В част-

ности,

большого класса функций при увеличении параметра происходит

разрушение прежде устойчивого цикла и замена его циклом

удвоенным

периодом. Это удвоение периода продолжается до бесконечности,

возни-

кает хаотическое поведение.

Во-вторых,

начале 70-х годов был популяризирован,

основном

Рюэлем,

раздел математики, называемый теорией динамических систем,

котором вводилось понятие «странного аттрактора». Основные задачи,

которые решались, были следующими: 1) как причинное уравнение (напри-

мер,

гидродинамические уравнения Навье

—

Стокса) может иметь реше-

ния

чисто статистическими свойствами

2) как теоретически предсказы-

вать статистические свойства. Это направление исследований объедини-

лось

итерационными идеями: стало

ясно,

что предельные бесконечные

«циклы» итерационных систем

могут

быть использованы для объяснения

турбулентности. Я решил изучать итерации функций после лекции С. Смей-

ла—

одного из создателей теории динамических систем,

Аспене летом

1975

г.

Моя

первая попытка понять проблему заключалась

исследовании

сложных свойств квадратичного преобразования

n+i

%х

—

Изучение прояснило механизм удвоения периода

привело

уравнениям

совершенно

другого

типа для определения значения

при которых проис-

ходит

удвоение периода. Новые уравнения были сложными, хотя прибли-

женное решение казалось возможным. Соответственно, когда

вернулся

из

Аспена,

численно определил значения некоторых параметров.

В то

*)Feigenbaum

Universal

Behavior

Nonlinear

Systems-—

Los

Alamos

Science.

1980,

v. 1,

No.

1, pp.

4—27.

Перевод

С. Г.

Тиходеева.

Фейгенбаум

—

сотрудник

Теоретического

отдела

Лос-Аламосской

научной

лаборатории,

Калифорнийский

университет,

Лос-Аламос,

шт.

Нью-Мексико,

США.

на

русский язык,

издательство «Наука». Главная редакция

физико-математической

литературы,

«Успехи

физических наук»,

1983.

344 М. ФЕЙГЕНБАУМ

время я никогда не пользовался большим компьютером, все, что у меня

было,— это карманный программируемый калькулятор. Но такие машин-

ки

считают очень медленно. Определенное значение параметра находится

итерациями

(методом Ньютона), причем каждый последующий шаг тре-

бует

итераций функции. Для 64-цикла это занимает 1 минуту на каждый

шаг метода Ньютона. В то же время при увеличении п становится все

сложнее определить положение требуемого решения. Однако я сразу же

понял,

что Х

сходятся, геометрически. Это позволило мне лредсказывать

каждое следующее решение с возрастающей при увеличении п точностью.

После

этого для получения необходимого значения требовался лишь, один

шаг метода Ньютона. Насколько мне известно, это наблюдение о геометри-

ческой сходимости не было никем сделано по той простой причине, что

решения

всегда получались автоматически на больших и быстрых компью-

терах!

• / .

То,

что имеется геометрическая сходимость, было уже неожидан-

ностью. Я заинтересовался этим по

двум

причинам. Во-первых, это позво-

лило

углубить

мое понимание проблемы. Во-вторых, поскольку скорость

сходимости есть число, инвариантное относительно гладких преобразова-

, ний, оно представляет математический интерес. Соответствнно, я истратил

часть дня на попытки выразить скорость сходимости

4,669

через известные

мне

математические константы. Дело не увенчалось успехом, если не счи-

тать того, что число хорошо запомнилось.

В этот момент П. Стайн напомнил мне, что удвоение периода не есть

уникальное свойство квадратичного отображения. Им обладает, например,

К sin лх

Однако моя теория существенно основывалась на том, что нелинейность

является просто квадратичной, а не трансцендентной. Соответственно

мой

интерес к проблеме упал.

Приблизительно

через месяц я решил численно определить значения %

трансцендентном случае. Эта задача решалась гораздо медленнее, чем

предыдущая. Снова стало очевидно, что значения X сходятся геометри-

чески и, что было совершенной неожиданностью, скорость сходимости

выражалась тем же числом

4,669,

так хорошо мне запомнившимся в

ходе

неудачных попыток подгонки.

Вспомним,

что в работе Н. Метрополиса, М. Стайна и П. Стайна было

показано,

что качественные особенности не зависят от конкретной итера-

ционной

схемы. Теперь я узнал, что точные количественные особенности

также не зависят от конкретного вида функции. Это открытие полностью

переворачивало обычный взгляд на вещи. Обычно полагают, что сходные

итерационные

схемы

могут

иметь качественно подобное поведение, но что

количественные предсказания зависят от конкретного вида функций.

Теория

универсальности показывает, что качественно сходные итерации

имеют одинаковое

количественное

поведение. Например, система диффе-

ренциальных уравнений задает определенное отображение. Вывод конкрет-

ного аналитического вида этого отображения находится обычно далеко

за пределами возможностей современных математических методов. Если,

однако,

отображение испытывает удвоение периода, теория универсаль-

ности

дает

точные количественные предсказания, независимо от конкрет-

ного вида отображения. В частности, теперь экспериментально установле-

но,

что некоторые жидкостные потоки переходят в турбулентное состояние

через, удвоение периода (субгармонические бифуркации). Одного этого

достаточно для применимости теории универсальности. И действительно,

она

правильно предсказывает путь перехода к турбулентности, не обра-

щаясь

к лежащим в основе уравнениям Навье — Стокса.

УНИВЕРСАЛЬНОСТЬ В ПОВЕДЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ 345

В природе происходят процессы

двух

типов: сложные, или хаоти-

ческие,

и простые, или упорядоченные. Задачей технологии является

создание устройств второго типа: отдельные части механизма, совершающие

отдельные упорядоченные действия, объединяются в единое целое для

выполнения

некоторой общей задачи. Так устроены, например, автомоби-

ли,

самолеты, радиоприемники и часы. Все они собраны из отдельных

простых частей, каждая из которых, по идее, отвечает за, одну какую-

нибудь функцию механизма. Важными технологическими проблемами

являются также

учет

и сведение к минимуму влияния неупорядоченных

процессов,

например сложных атмосферных явлений, вихрей в

турбулент-

ном

потоке, шумов в электронной

схеме

и т. д. Ниже пойдет речь именно

таких сложных явлениях.

Поведение шумового сигнала нерегулярно и трудно предсказуемо.

Если,

однако, проанализировать достаточно длинную запись такого сигна-

ла, может обнаружиться, что его амплитуда находится в определенном

узком диапазоне определенную долю времени. Если анализ

другой

записи

сигнала обнаружит такую же долю времени, мы сможем описать шум

статистически.

Это значит, что хотя и нельзя предсказать, какова

будет

следующая амплитуда, но вполне возможно оценить вероятность достиже-

ния

сигналом каких-то определенных значений. За последние сто лет

утвердился именно статистический

подход

к неупорядоченным процессам.

Поэтому исследование их заключается в определении вероятностей и,

исходя из вероятностей, того, что нас в данном

случае

интересует, напри-

мер какое влияние оказывает турбулентность

воздуха

на лобовое сопро-

тивление самолета.

Мы

знаем, что детерминированные и

простые

закономерности

могут

вести себя статистическим (или случайным) образом. Так, в современных

электронно-вычислительных машинах имеются симулирующие хаоти-

ческий

процесс «генераторы случайных чисел». Такие генераторы просто

передвигают запятую в рациональном числе с достаточно длинным пе-

риодом. Соответственно, можно предсказать, каким

будет

ге-е полученное

число.

И все же последовательность полученных таким образом чисел

производит впечатление настолько неупорядоченной и случайной, что все

статистические тесты подтвердят случайное происхождение этих чисел.

Это явление обозначается термином

«псевдослучайность».

Мы рассмотрим

данной работе, не являются ли псевдослучайными различные хаоти-

ческие природные процессы (вопреки сложившемуся, но ошибочному

мнению,

что это не поддается проверке). То, что некоторые очень простые

алгоритмы для получения случайных чисел

ведут

себя полностью анало-

гично

естественным случайным процессам, представляется совершенно

замечательным. Например, сейчас имеется убедительное доказательство

того, что при помощи простой схемы, описанной в этой статье, можно

объяснить, каким образом ламинарный поток жидкости становится

турбу-

лентным.

Этот же метод пригоден для рассмотрения

других

естественно-

научных проблем: изменений в популяции от поколения к поколению,

шумов в разнообразных механических, электрических и химических

осцилляторах. Так же можно исследовать и различные гамильтоновы

системы, описывающиеся классической механикой, например Солнечную

систему.

Все указанные процессы имеют

следующую

общую

черту:

по мере

изменения

какого-то внешнего параметра (например, температуры) пове-

дение системы меняется от простого к хаотическому. Говоря точнее, имеет-

ся

определенный диапазон значений внешнего параметра, в котором пове-

346

М.

ФЕЙГЕНБАУМ

дение

системы упорядочено и

периодично

(т. е. самовоспроизводится в каж-

дый

период

времени Т). Вне этого диапазона процесс перестает воспроиз-

водиться через Т секунд; этого времени почти достаточно, но, в действи-

тельности, требуются два интервала

Т,

чтобы процесс воспроизвелся, т. е.

период удваивается и становится равным

IT.

Эта новая периодичность

сохраняется внутри некоего нового диапазона значений параметра, пока

не

будет

достигнуто новое критическое значение, после чего поведение

только

почти

воспроизводится через

2Г

секунд, на самом

деле

для этого

требуется уже

4Г

секунд. Процесс последовательного удвоения периода

продолжается дальше (причем интервал значений параметра, при котором

период равен

Т,

с ростом п уменьшается), пока при определенном значе-

нии

параметра период не станет

бесконечным,

а поведение системы переста-

нет быть периодическим. Следовательно, удвоение периода — это харак-

терная черта перехода системы от простого периодического к сложному

непериодическому движению. Удвоение периода наблюдается во

всех

упомянутых выше процессах. В пределе хаотического непериодического

движения имеется единственное и поэтому

универсальное

решение, общее

для

всех

систем, испытывающих удвоение периода. Это обстоятельство

имеет замечательные следствия. Пусть

—

значение параметра (для

каждой конкретной системы), при котором период удваивается в

п-ж

раз.

Тогда оказывается, что при больших п

геометрически

сходится к А»

(при

котором движение становится апериодическим). Это означает, что при

больших п

—

Л„

S-",

(1)

где значение

(скорости

перехода к хаотическому движению) фиксирова-

но.

Иначе говоря, если

то

быстро приближается к постоянной величине 6. (Как правило,

совпадает с б с точностью до нескольких значащих цифр уже после

небольшого числа удвоений периода.) Совершенно замечательным (поми-

мо того, что всегда наблюдается геометрическая сходимость) представляет-

ся

то, что у

всех

систем, испытывающих удвоение периода, значение б

одинаково

и равно универсальному числу

б =

4,6692016...

(3)

Именно

такой является скорость перехода к беспорядку осцилляторов,

популяций,

жидкостей и вообще

всех

систем, испытывающих удвоение

периода! Универсальность теории такова, что большинство измеримых

параметров

любой

из таких систем в пределе хаотического движения может

быть определено без помощи специальных, описывающих данную систему

уравнений, т. е. если система переходит к хаотическому поведению путем

удвоения периода

(качественная

характеристика), ее

количественные

ха-

рактеристики становятся полностью заданными. Этот вывод подобен след-

ствиям современной

теории

фазовых

переходов,

которой несколько ка-

чественных характеристик системы, совершающей фазовый переход, осо-

бенно

размерность, определяют

универсальные

критические экспоненты.

Действительно, на

формальном

уровне эти теории идентичны в том смысле,

что обе они являются теориями неподвижной точки,

число б, например,

можно рассматривать как критическую экспоненту. Соответственно, для

того чтобы разобраться в общем случае, достаточно рассмотреть простейшую

(из

обладающих таким поведением) систему.

УНИВЕРСАЛЬНОСТЬ В ПОВЕДЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ 347

ФУНКЦИОНАЛЬНАЯ

ИТЕРАЦИЯ

Генератор случайных чисел — это пример простой итерационной

схемы, обладающей сложным поведением. Каждое следующее псевдослу-

чайное число вычисляется путем некоторой операции над предыдущим

псевдослучайным числом. Другими словами, для получения последова-

тельности таких чисел каждый раз вычисляется некоторая функция.

Пусть / является этой функцией, а

—

первым числом. Тогда последова-

тельность псевдослучайных чисел имеет вид

, х

. . .,

. . ., где

+l=f

Ы,

Говорят, что она образована путем

функциональной

итерации,

п-ш.

эле-

мент последовательности равен

=/(/(••

•/ (/

(*„))

• • •)) ^

(*о),

(5)

где п — общее число вычислений функции /.

(/"

(х) не есть га-я степень /,

это

— п-я

итерация

/.) Отметим следующее свойство итераций:

{Г

(*))

(х))

{х),

(6)

поскольку каждое из выражений означает просто т -\- re-кратное вычисле-

ние

функции /. Очевидно, что

f (x) = х. (7)

Удобно обозначить функциональную итерацию специальным символом, °,

так

что

/«

+ ". (8)

Теперь / в (5) является определенной и вычислимой функцией, поэтому,

принципе,

функционально зависит от

Если

функция / является

линейной,

например

(х)

= ах, (9)

где а — постоянная, та

(x)

(10)

(11)

есть решение

рекуррентного

соотношения

типа (4), которое в данном слу-

чае имеет вид

п+1

ах

(12)

Если

\ а |

<1,

то

геометрически сходится к нулю (со скоростью На).

Этот пример является выделенным, поскольку линейность функции /

позволяет точно вычислить функцию

Для того чтобы образовать последовательность псевдослучайных

чисел, мы должны выбрать

нелинейную

функцию /. Возьмем в качестве /

/ =

—

х\

(13)

Тогда

является многочленом от х степени

2™.

G ростом п этот многочлен

быстро становится очень громоздким. Более того, его коэффициенты

являются многочленами степени

2™~

от а, при больших п их очень трудно

348

М,

ФЕЙГЕНВАУМ

Рис.

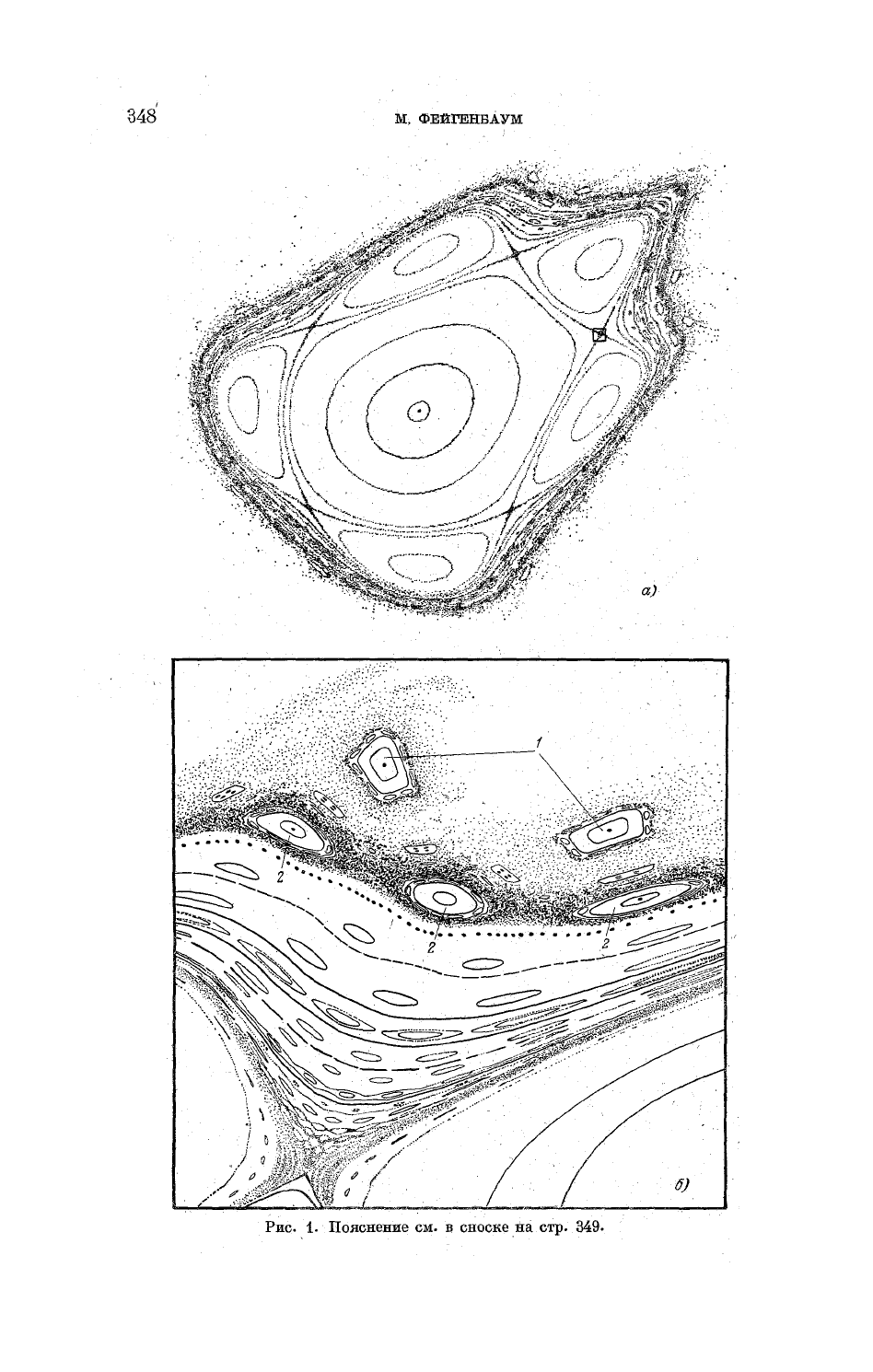
1. Пояснение см. в сноске на стр. 349.

УНИВЕРСАЛЬНОСТЬ В ПОВЕДЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ 349

вычислять. Даже при

—

является многочленом

z™"

степени от а.

Эти многочлены нетривиальны, что очевидно хотя бы из того, что для

определенных значений а последовательность чисел, начинающихся с лю-

бого из интервала

(а

— а

а),

имеет все математические свойства последо-

вательности случайных чисел. Для иллюстрации на рис. 1 *) показаны

последовательные итерации аналогичной, но двумерной функции

П+1

—Уп

П,

Как

и в (4), по начальной паре координат

(х

применяя (14), можно

вычислить

следующую

пару

(ж

затем

(х

)

и т. д. Для некоторых

начальных точек все итерации попадают на кривую в форме

эллипса,

*) Элементарное двумерное преобразование может вести себя бесконечно сложным

образом.

Нижний

рис. 1 есть увеличенная область в квадратике на верхнем рис. 1.

При

помощи теории, предложенной

Митчелом

Фейгенбаумом и описанной им

статье

«Универсальность в поведении нелинейных систем», может быть описан пере-

ход (посредством удвоения периода) от простого поведения к сложному в широком

классе нелинейных диссипативных систем. Использованное для построения рис. 1

преобразование сохраняет фазовый объем и

соответствует

консервативной, а не дис-

сипативной

системе. Экспериментально установлено, что система такого типа может

жспытывать

удвоение периода, и

Митчел

надеется обобщить теорию универсальности

на

гамильтоновы системы.

Рис.

1 был построен при помощи преобразования

' = у _

у' =

—

х,

(где

—0,4224),

многократно примененного к некоторому семейству начальных

точек. Это квадратичное преобразование сохраняет площади и может рассматри-

ваться как отображение Пуанкаре некоторой консервативной системы. Аналогич-

ное

отображение Пуанкаре имеет, например, поршень, поддерживаемый в поле тя-

жести

одночастичяым

газом.

Приблизительно 50 начальных точек, использованных для построения рис. 1,

можно разделить на два множества. Из точек первого множества получаются ите-

рации,

лежащие на

эллипсоподобных

кривых. Например, из 3 начальных точек полу-

чаются, соответственно, центральные точки, меньшие внутренние овалы и большие

овалы, в кластерах, обозначенных на рис.

1,6

цифрой 1. Одна начальная точка образу-

ет центральные точки обоих изображенных на рисунке кластеров 1 (как и кластеров,

не

попавших в поле изображения). Из начальных точек второго типа образуется

«дымка»

итераций, хаотически попадающих в определенные области рисунка. На-

пример,

плотная дымка, окружающая три кластера 2, образована только одной на-

чальной точкой.

Именно

эта дымка и

соответствует

статистическому поведению систе-

мы.

Поведение итераций является еще гораздо более сложным, чем показано на ри-

сунке.

Именно,

если увеличить область плотной дымки, расположенную ровно по

•середине

между

соседними кластерами 2, получится совершенно аналогичная картина

•с

островами и дымкой, и т. д., до бесконечности.

Такое поведение можно считать следствием неустойчивостей (таких, скажем,

как

в плазме), которые привели к неконтролируемому поведению системы. В рамках

аналогии с консервативной системой вся плоскость является поверхностью постоян-

ной

энергии. Траектория системы, подчиняющейся статистической механике, долж-

на

хаотически перемещаться по всей этой плоскости. Совершенно очевидно, что с

нашей

системой этого не происходит: некоторые начальные точки порождают траекто-

рии,

циркулирующие вокруг одного из эллиптических островов, или «инвариантных

торов». Существование таких торов есть нарушение статистической механики, но

оно

следует

из знаменитой теоремы Колмогорова — Арнольда — Мозера. Надежда

на

обоснование статистической механики для классических систем — в поиске воз-

можностей разрушения этих торов. Поскольку удвоение периода есть способ последо-

вательного разрушения торов, обобщение существующей теории универсальности

может описать этот процесс количественно. Это обобщение теории еще не построено,

но

активно разрабатывается. Кроме объяснения того, как гамильтоновы системы

приходят к эргодическому поведению, эта теория может дать ответ на противополож-

ный

вопрос: как избежать хаотизации данной конкретной системы. Это имеет большое

значение,

например, для проблемы управляемого термоядерного синтеза.

(Прим-

редакции

журнала

«L. A.

Science».)

350

ФвагЕнвАУм

то время как для

других

распределены

«усредненно»

по некоторой

области. Представляется очевидным, что столь разнообразные типы пове-

дения,

показанные на рис. 1, не описываются какой-либо точной форму-

лой,

т. е. хотя итерируемая функция (14) легко выписывается, нельзя

получить

и-ю

итерацию в виде простой функции

(х

Другими слова-

ми,

если многократно итерировать простейшую нелинейную функцию,

можно получить весьма сложное поведение. Причем, поскольку повторно

вычисляется^

одна и та же функция, можно ожидать появления всего

нескольких типов самосогласованного поведения, определяемых не кон-

кретным видом итерируемой функции, а самим фактом ее многократного

вычисления.

Такие самосогласованные типы поведения возникают в пре-

деле

бесконечного удвоения периода и имеют отчетливую

структуру,

которая

может быть a priori определена среди сложных конфигураций,

показанных

на рис. 1.

НЕПОДВИЖНЫЕ

ТОЧКИ ФУНКЦИОНАЛЬНЫХ ИТЕРАЦИИ

Рассмотрим теперь свойства функции (13). Нас интересует поведение

системы после большого числа итераций. Как мы уже знаем, многократные

итерации

/ быстро становятся очень сложными. В одном

случае

этого не

происходит — если первая итерация

в точности равна

Разумеется,

это

условие выполняется не для

всех

точек

х,

а выделяет не меняющиеся

точки

называемые

неподвижными

точками

функции /. Итерационная

последовательность для таких точек имеет вид

, х

. . .,

поведение системы

статично

или может рассматриваться как периоди-

ческое с периодом 1.

Неподвижные точки (13) легко определить. Для

удобства

мы

будем

использовать несколько

другой

вид (13), получаемый сдвигом и некоторы-

ми

переопределениями:

/ (х) =

4Lr

(1 — х). (15)

При

любых % точка х = 0 является неподвижной. В самом деле, функция

(15) имеет две неподвижные точки, являющиеся решениями уравнения

я*

= /

(х*)

4^*

(1 —

х*)

(16)

равные

0, x$

i-\.

(17)

Функция

(15) при х = 1/2 достигает максимального значения, равно-

го

К.

Кроме того, если

0 и х лежит в интервале (0, 1), / (х) положи-

тельна. Поэтому, если 0 ^

^ 1, любая итерация точки 0

1 также

лежит в интервале (0, 1). Поэтому в дальнейшем мы рассмотрим только

значения

х и

К,

лежащие

между

0 и 1. Из (16)

следует,

что, в отличие от

случая 0

< 1/4, когда имеется только одна неподвижная точка

х*

= 0, при 1/4 ^ % ^ 1 обе неподвижных точки принадлежат рассматри-

ваемому интервалу. Например, если положить

= 1/2 и начать с непод-

вижной

точки

х*

= 1/2 (т. е. положить

= 1/2), то

= . . .

1/2.

Аналогично, если

= 0,

...=0,и

проблема вычисления п-й

итерации

решается тривиально.

Что произойдет, если мы выберем

не равным неподвижной точке?

Чтобы разобраться в происходящем, сделаем следующее графическое

построение.

Построим графики функций у = f (x) и у = х. В точках

пересечения графиков имеем х = у = / (х), поэтому пересечения являются

как

раз неподвижными точками. Теперь, если выбрать определенное зна-

чение

и отложить его на

ж-оси,

равно ординате / (х) при х =

УНИВЕРСАЛЬНОСТЬ

В ПОВЕДЕНИИ НЕЛИНЕЙНЫХ СИСТЕМ

351

Чтобы получить

перед вычислением / надо перенести значение

на

ж-ось.

Эта операция есть отражение от прямой у = х. В итоге, чтобы

получить последовательные итерации

надо:

1. провести вертикальную прямую до пересечения с графиком функ-

ции

(х);

2. провести горизонтальную прямую до пересечения с линией у =

х;

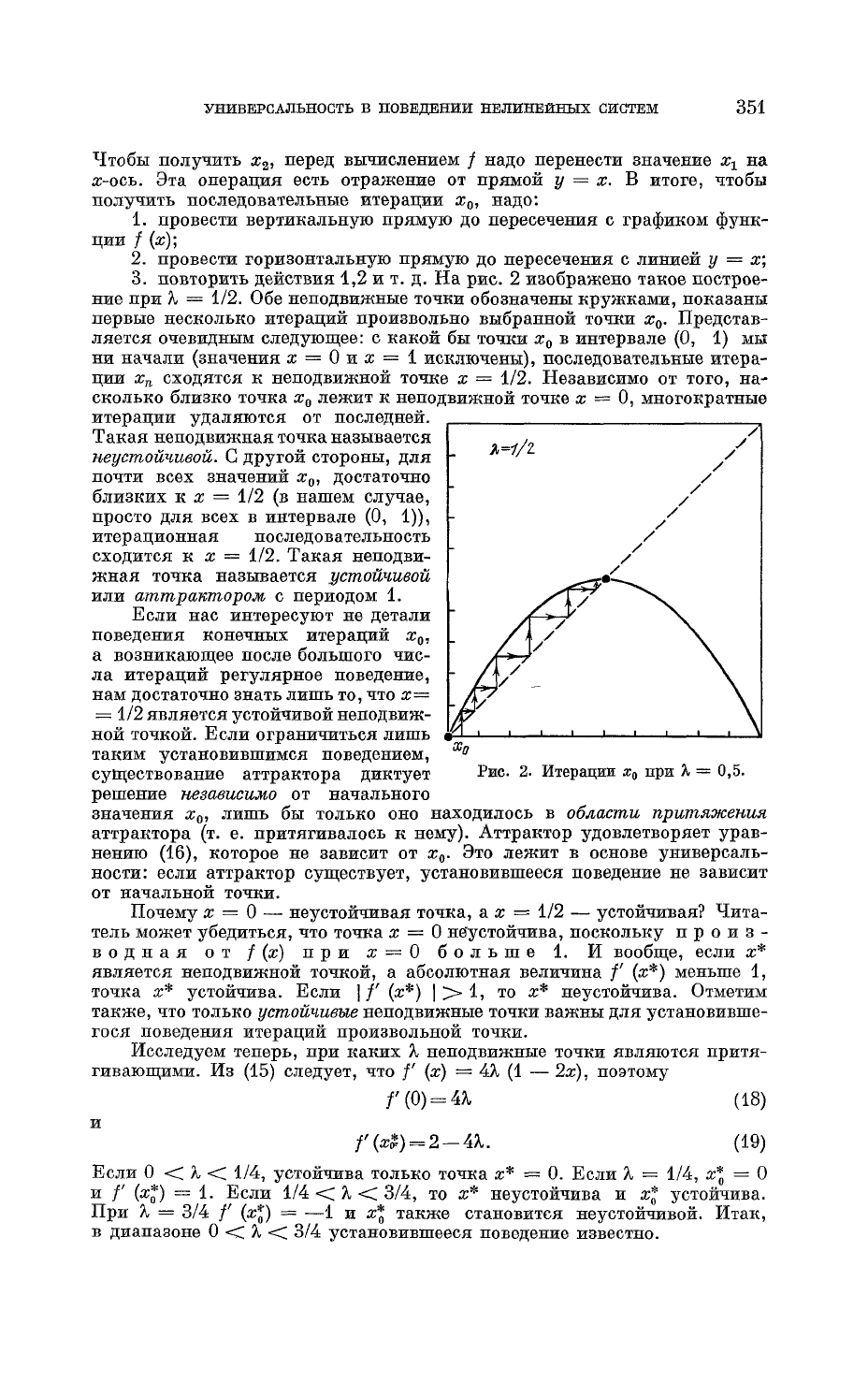
3. повторить действия 1,2 и т. д. На рис. 2 изображено такое построе-

ние

при X

1/2. Обе неподвижные точки обозначены кружками, показаны

первые несколько итераций произвольно выбранной точки

Представ-

ляется очевидным следующее: с какой бы точки

в интервале (0, 1) мы

ни

начали (значения х = 0 и х = 1 исключены), последовательные итера-

ции

сходятся к неподвижной точке х = 1/2. Независимо от того, на-

сколько

близко точка

лежит к неподвижной точке х = 0, многократные

итерации

удаляются от последней.

Такая

неподвижная точка называется

неустойчивой.

другой

стороны, для

почти

всех

значений

достаточно

близких к х = 1/2 (в нашем случае,

просто для

всех

в интервале (0, 1)),

итерационная

последовательность

сходится к х = 1/2. Такая неподви-

жная

точка называется

устойчивой

или

аттрактором

с периодом 1.

Если

нас интересуют не детали

поведения конечных итераций

а возникающее после большого чис-

ла итераций регулярное поведение,

нам

достаточно знать лишь то, что

х—

1/2 является устойчивой неподвиж-

ной

точкой. Если ограничиться лишь

таким

установившимся поведением,

существование аттрактора диктует

решение

независимо

от начального

значения

лишь бы только оно находилось в

области

притяжения

аттрактора (т. е. притягивалось к нему). Аттрактор удовлетворяет урав-

нению

(16), которое не зависит от

Это лежит в основе универсаль-

ности:

если аттрактор

существует,

установившееся поведение не зависит

от начальной точки.

Почему х = 0 — неустойчивая точка, а х = 1/2 — устойчивая? Чита-

тель может убедиться, что точка х = 0 неустойчива, поскольку

произ-

водная от / (х) при х = 0 больше 1. И вообще, если х*

является неподвижной точкой, а абсолютная величина /' (х*) меньше 1,

точка х* устойчива. Если | /'

(х*)

1, то х* неустойчива. Отметим

также, что только

устойчивые

неподвижные точки важны для установивше-

гося поведения итераций произвольной точки.

Исследуем теперь, при каких X неподвижные точки являются притя-

гивающими. Из (15)

следует,

что /' (х) = АХ (1 — 2х), поэтому

/' (0) =

4Л,

(18)

/'(ж$)

= 2 — АХ. (19)

Если

1/4, устойчива только точка х* = 0. Если X = 1/4,

х*

= 0

(х*)

= 1. Если 1/4

<С

X < 3/4, то х* неустойчива и а;* устойчива.

При

X = 3/4 /'

(х*

)

•—1

х*

также становится неустойчивой. Итак,

диапазоне 0

3/4 установившееся поведение известно.

Рис.

2. Итерации

при

0,5.

352

М.

ФЁЙГЕНБАУМ

ВОЗНИКНОВЕНИЕ

ПЕРИОДА

2 ИЗ

НЕПОДВИЖНОЙ

ТОЧКИ

Что происходит с системой, если 3/4

<С

1, когда притягивающие

неподвижные точки

отсутствуют?

Мы увидим, что если значение X немного

превысило величину 3/4, итерации / испытывают удвоение периода. Это

означает, что вместо устойчивого цикла с периодом 1, соответствующего

одной неподвижной точке, система

имеет устойчивый цикл

спериодом2,

т.

•

е. цикл, содержащий две точки.

Поскольку эти точки являются непод-

вижными точками функции

(дваж-

ды вычисленной функции/) и посколь-

ку устойчивость определяется произ-

водной функции в

неподвижных

точ-

ках, займемся теперь

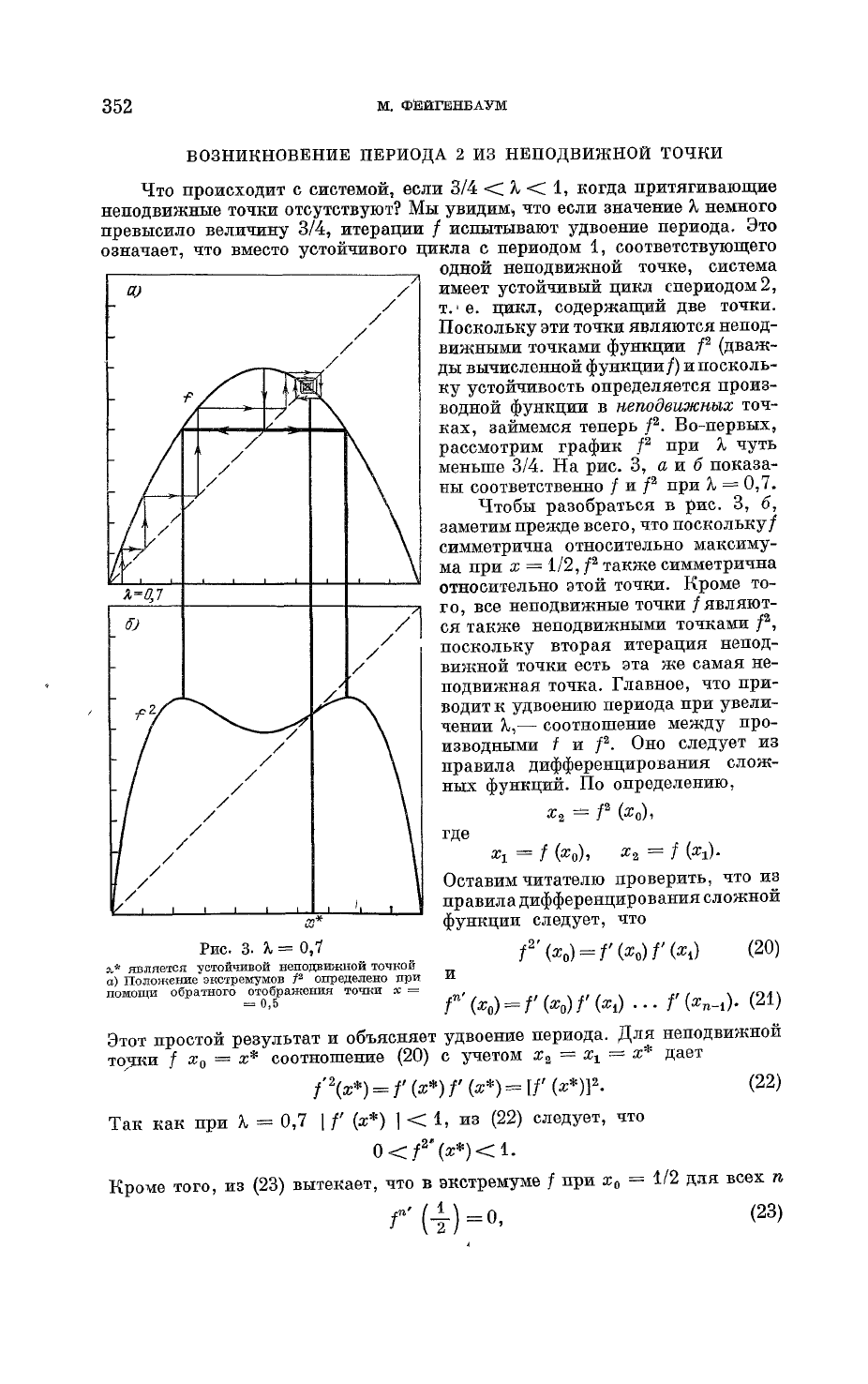
Во-первых,

рассмотрим график

при X

чуть

меньше 3/4. На рис. 3,

и б показа-

ны

соответственно / и

при X = 0,7.

Чтобы разобраться в рис. 3, б,

заметим прежде всего, что поскольку/

симметрична относительно максиму-

ма при х = 1/2,

также симметрична

относительно этой точки. Кроме то-

го, все неподвижные точки /являют-

ся

также неподвижными точками

поскольку вторая итерация непод-

вижной точки есть эта же самая не-

подвижная точка. Главное, что при-

водит к удвоению периода при увели-

чении X,— соотношение

между

про-

изводными f и

Оно

следует

из

правила дифференцирования слож-

ных функций. По определению,

(х

где

= /

(Х

= /

(Х

Оставим читателю проверить, что из

правила

дифференцирования сложной

функции

следует,

что

Рис.

= 0,7

х*

является устойчивой

неподвижной

точкой

а)

Положение

экстремумов Р определено при

помохци

обратного

^отображения

точки х =

{Хо)

{Хо

)

(

)

(20)

Этот простой

результат

и объясняет удвоение периода. Для неподвижной

точки /

= х* соотношение (20) с

учетом

х*

дает

(

{

(a*)]*.

(22)

Так

как при X = 0,7 | /' (ж*) ] <

из (22)

следует,

что

(я*)<1.

Кроме того, из (23) вытекает, что в экстремуме / при

= 1/2 для

всех

г'

(4)=о.

(23)