Firk F.W.K. Essential Physics. Part 1. Relativity, Particle Dynamics, Gravitation, and Wave Motion
Подождите немного. Документ загружается.

2
KINEMATICS: THE GEOMETRY OF MOTION
2.1 Velocity and acceleration
The most important concepts in Kinematics — a subject in which the properties of
the forces responsible for the motion are ignored — can be introduced by studying the
simplest of all motions, namely that of a point P moving in a straight line.
Let a point P[t, x] be at a distance x from a fixed point O at a time t, and let it be at
a point P´[t´, x´] = P´[t + ∆t, x + ∆x] at a time ∆t later. The average speed of P in the
interval ∆t is
<v
p
> = ∆x/∆t. (2.1)
If the ratio ∆x/∆t is not constant in time, we define the instantaneous speed of P at time
t as the limiting value of the ratio as ∆t → 0:
•
v
p
= v
p
(t) = limit as ∆t → 0 of ∆x/∆t = dx/dt = x = v
x
.
The instantaneous speed is the magnitude of a vector called the instantaneous
velocity of P:
v = dx/dt , a quantity that has both magnitude and direction. (2.2)
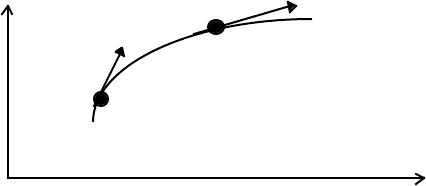
A space-time curve is obtained by plotting the positions of P as a function of t:
x v
p´
v
p
P´
P
O t

K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 34
The tangent of the angle made by the tangent to the curve at any point gives the value of
the instantaneous speed at the point.
The instantaneous acceleration, a , of the point P is given by the time rate-of-change
of the velocity
••
a = dv/dt = d(dx/dt)/dt = d
2
x/dt
2
= x . (2.3)
A change of variable from t to x gives
a = dv/dt = dv(dx/dt)/dx = v(dv/dx). (2.4)
This is a useful relation when dealing with problems in which the velocity is given as a
function of the position. For example
v v
P
P
v
α
O N Q x
The gradient is dv/dx and tanα = dv/dx, therefore
NQ, the subnormal, = v(dv/dx) = a
p
, the acceleration of P. (2.5)
The area under a curve of the speed as a function of time between the times t
1
and t
2
is
[A]
[t1,t2]
= ∫
[t1,t2]
v(t)dt = ∫
[t1,t2]
(dx/dt)dt = ∫
[x1,x2]
dx = (x
2
– x
1
)
= distance travelled in the time t
2
– t
1
. (2.6)
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 35
The solution of a kinematical problem is sometimes simplified by using a graphical
method, for example:
A point A moves along an x-axis with a constant speed v
A
. Let it be at the origin O
(x = 0) at time t = 0. It continues for a distance x
A
, at which point it decelerates at a
constant rate, finally stopping at a distance X from O at time T.
A second point B moves away from O in the +x-direction with constant
acceleration. Let it begin its motion at t = 0. It continues to accelerate until it reaches a
maximum speed v
B
max
at a time t
B
max
when at x
B
max
from O. At x
B
max
, it begins to decelerate
at a constant rate, finally stopping at X at time T: To prove that the maximum speed of B
during its motion is
v
B
max
= v
A
{1 – (x
A
/2X)}
–1
, a value that is independent of the time at which
the maximum speed is reached.
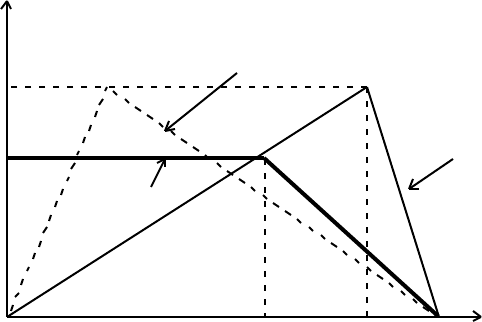
The velocity-time curves of the points are
v
A possible path for B
v
B
max
v
A
B
A
O
t = 0 t
A
t
B
max
T t
x = 0 x
A
x
B
max
X
The areas under the curves give X = v
A
t
A
+ v
A
(T – t
A
)/2 = v
B
max
T/2, so that
v
B
max
= v
A
(1 + (t
A
/T)), but v
A
T = 2X – x
A
, therefore v
B
max
= v
A
{1 – (x
A
/2X)}
–1
≠ f(t
B
max
).
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 36
2.2 Differential equations of kinematics
If the acceleration is a known function of time then the differential equation
a(t) = dv/dt (2.7)
can be solved by performing the integrations (either analytically or numerically)
∫a(t)dt = ∫dv (2.8)
If a(t) is constant then the result is simply
at + C = v, where C is a constant that is given by the initial conditions.
Let v = u when t = 0 then C = u and we have
at + u = v. (2.9)
This is the standard result for motion under constant acceleration.
We can continue this approach by writing:
v = dx/dt = u + at.
Separating the variables,
dx = udt + atdt.
Integrating gives
x = ut + (1/2)at
2
+ C´ (for constant a).
If x = 0 when t = 0 then C´ = 0, and
x(t) = ut + (1/2)at
2
. (2.10)
Multiplying this equation throughout by 2a gives
2ax = 2aut + (at)
2
= 2aut + (v – u)
2
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 37
and therefore, rearranging, we obtain
v
2
= 2ax – 2aut + 2vu – u
2
= 2ax + 2u(v – at) – u
2
= 2ax + u
2
. (2.11)
In general, the acceleration is a given function of time or distance or velocity:
1) If a = f(t) then
a = dv/dt =f(t), (2.12)
dv = f(t)dt,
therefore
v = ∫f(t)dt + C(a constant).
This equation can be written
v = dx/dt = F(t) + C,
therefore
dx = F(t)dt + Cdt.
Integrating gives
x(t) = ∫F(t)dt + Ct + C´. (2.13)
The constants of integration can be determined if the velocity and the position are known
at a given time.
2) If a = g(x) = v(dv/dx) then (2.14)
vdv = g(x)dx.
Integrating gives
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 38
v
2
= 2∫g(x)dx + D,
therefore
v
2
= G(x) + D
so that
v = (dx/dt) = ±√(G(x) + D). (2.15)
Integrating this equation leads to
±∫dx/{√(G(x) + D)} = t + D´. (2.16)
Alternatively, if
a = d
2
x/dt
2
= g(x)
then, multiplying throughout by 2(dx/dt)gives
2(dx/dt)(d
2
x/dt
2
) = 2(dx/dt)g(x).
Integrating then gives
(dx/dt)
2
= 2∫g(x)dx + D etc.
As an example of this method, consider the equation of simple harmonic motion (see later
discussion)
d
2
x/dt
2
= –ω
2
x. (2.17)
Multiply throughout by 2(dx/dt), then
2(dx/dt)d
2
x/dt
2
= –2ω
2
x(dx/dt).
This can be integrated to give
(dx/dt)
2
= –ω
2
x
2
+ D.
If dx/dt = 0 when x = A then D = ω
2
A
2
, therefore
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 39
(dx/dt)
2
= ω
2
(A
2
– x
2
) = v
2
,
so that
dx/dt = ±ω√(A
2
– x
2
).
Separating the variables, we obtain
– dx/{√(A
2
– x
2
)} = ωdt. (The minus sign is chosen because dx and dt have
opposite signs).
Integrating, gives
cos
–1
(x/A) = ωt + D´.
But x = A when t = 0, therefore D´ = 0, so that
x(t) = Acos(ωt), where A is the amplitude. (2.18)
3) If a = h(v), then (2.19)
dv/dt = h(v)
therefore
dv/h(v) = dt,
and
∫dv/h(v) = t + B. (2.20)
Some of the techniques used to solve ordinary differential equations are discussed
in Appendix A.
2.3 Velocity in Cartesian and polar coordinates
The transformation from Cartesian to Polar Coordinates is represented by the
linear equations

K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 40
x = rcosφ and y = rsinφ, (2.21 a,b)
or
x = f(r, φ) and y = g(r, φ).
The differentials are
dx = (∂f/∂r)dr + (∂f/∂φ)dφ and dy = (∂g/∂r)dr + (∂g/∂φ)dφ.
We are interested in the transformation of the components of the velocity vector under
[x, y] → [r, φ]. The velocity components involve the rates of change of dx and dy with
respect to time:
dx/dt = (∂f/∂r)dr/dt + (∂f/∂φ)dφ/dt and dy/dt = (∂g/∂r)dr/dt + (∂g/∂φ)dφ/dt
or
•
•
•
•
•
•
x = (∂f/∂r)r + (∂f/∂φ)φ and y = (∂g/∂r)r + (∂g/∂φ)φ. (2.22)
But,
∂f/∂r = cosφ, ∂f/∂φ = –rsinφ, ∂g/∂r = sinφ, and ∂g/∂φ = rcosφ,
therefore, the velocity transformations are
•
•
•
x = cosφ r – sinφ(r φ) = v
x
(2.23)
and
•
•
•
y = sinφ r + cosφ(r φ) = v
y
. (2.24)
These equations can be written
v
x
cosφ –sinφ dr/dt
= .
v
y
sinφ cosφ rdφ/dt
Changing φ → –φ, gives the inverse equations
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 41
dr/dt cosφ sinφ v
x
=
rdφ/dt –sinφ cosφ v
y
or
v
r
v
x
=
c
(φ) . (2.25)
v
φ
v
y
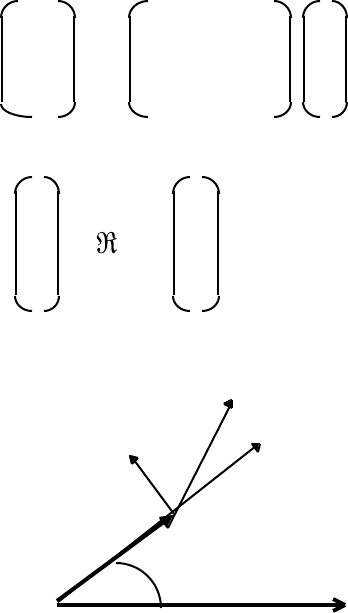
The velocity components in [r, φ] coordinates are therefore
V
•
•
|v
φ
| = r φ = rdφ/dt |v
r
| = r =dr/dt
P[r, φ]
r +φ , anticlockwise
O x
The quantity dφ/dt is called the angular velocity of P about the origin O.
2.4 Acceleration in Cartesian and polar coordinates
We have found that the velocity components transform from [x, y] to [r, φ]
coordinates as follows
•
•
•
v
x
= cosφ r – sinφ(r φ) = x
and
•
•
•
v
y
= sinφ r + cosφ(r φ) = y.
The acceleration components are given by
a
x
= dv
x
/dt and v
y
= dv
y
/dt
We therefore have
•
•
a
x
= (d/dt){cosφ r – sinφ(r φ)} (2.26)
K I N E M A T I C S : T H E G E O M E T R Y O F M O T I O N 42
••
•
• •
••
= cosφ(r – r φ
2
) – sinφ(2r φ + r φ)
and
•
• •
a
y
= (d/dt){sinφ r + cosφ(r φ)} (2.27)
• •
••
••
•
= cosφ(2r φ + r φ) + sinφ(r – r φ
2
).
These equations can be written
a
r
cosφ sinφ a
x
= . (2.28)
a
φ
–sinφ cosφ a
y
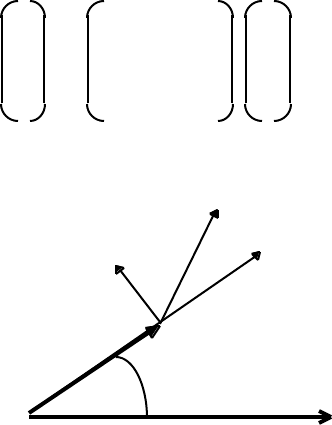
The acceleration components in [r, φ] coordinates are therefore
A
• •
••
|a
φ
| = 2r φ + r φ
••
•
|a
r
| = r – r φ
2
P[r, φ]
r φ
O x
These expressions for the components of acceleration will be of key importance in
discussions of Newton’s Theory of Gravitation.
We note that, if r is constant, and the angular velocity ω is constant then
••
•
a
φ
= r φ = rω = 0, (2.29)
•
a
r
= – r φ
2
= – rω
2
= – r(v
φ
/r)
2
= – v
φ
2
/r, (2.30)
and
•
v
φ
= r φ = rω. (2.31)
These equations are true for circular motion.
