Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

650 10 Glaciers and Ice Sheets

10.2.7 The Grounding Line

In the transition region, we need to retain terms which are of importance in both ice

sheet and ice shelf approximations. This requires us to rescale the ice sheet scaled

variables in the following way:

x −x

∼γ, z,b ∼β, s ∼δβ, u ∼

,w∼

t ∼β, p,τ

∼

δβ

,τ

∼

δβ

,τ∼

δβ

(10.147)

where x

is the grounding line position; the parameters β and γ are deﬁned by

β =





n+2

,γ=βε. (10.148)

This rescaling reintroduces the full Stokes equations. Denoting the rescaled vari-

ables (except time) by capitals, and writing

x −x

(t) =γX, t =βt

∗

, (10.149)

we derive the model

=0,

0 =−S

−P

0 =−P

−T

n−1

(10.150)

The boundary conditions are the following. On the surface Z =δS,

+δ(P −T

=0,

P +T

+δT

=0,

W =δ(γS

∗

−˙x

) +δUS

−γa,

(10.151)

where ˙x

∗

. On the base Z = B, when X>0,

−T

+(−P +T

=(S +B)B

S +B =−[P +T

W =γB

∗

−˙x

+UB

−γm,

(10.152)

and when X<0,

W =0,U=0, (10.153)

where we assume that the sliding velocity is zero for grounded ice.

This simple assumption is not very realistic, since it is most likely that in the vicinity of the

grounding line, the basal ice will be at the melting point, and the sliding velocity will be non-zero.

Where ice streams go aﬂoat, the velocity is almost entirely due to basal sliding.

10.2 The Shallow Ice Approximation 651

To leading order, we can approximate the top surface boundary conditions as

γ →0 and also δ →0by

=P +T

=W =0onZ =0. (10.154)

The kinematic condition at the shelf base is approximately

W =−˙x

+UB

on Z =B. (10.155)

In addition, the solution must be matched to the outer (sheet and shelf) solutions.

We consider ﬁrst the ice sheet behaviour as x → x

. We suppose that the ice sheet

is described in one dimension by (10.45), thus

=−q

+a, (10.156)

where the ice ﬂux is (in ice sheet scaled variables)

q =

(s −b)

n+2

(−s

)

n +2

. (10.157)

We can carry out a local analysis near x

similar to those in Sect. 10.2.5.Asx →

, s −b → 0 (since s −b ∼ β 1), but the ice ﬂux is non-zero; in this case we

ﬁnd that always

H =s −b ∼C(x

−x)

2(n+1)

,q∼q



2(n +1)



2n+2

n +2

. (10.158)

When the surface slope is computed from this, we ﬁnd that the requisite matching

condition for the slope written in terms of the transition zone scalings is that

∼−

2(n +1)

(−δX)

n+2

2(n+1)

as X →−∞. (10.159)

Clearly the presence of the small parameter δ does not allow direct matching of the

transition zone to the ice sheet.

The problem is easily resolved, however. There is a ‘joining’ region in which

X =

X/δ, S =

S/δ, and then also P,T

,W ∼ δ; the resultant set of equations is

easily solved (it is a shear layer like the ice sheet), and we ﬁnd

S =B



(−B

)

2(n+1)/n

−

2(n +1)



(n +2)q



1/n



n/(2n+2)

, (10.160)

where B = B

at x = x

. Expanding this as

X → 0, we ﬁnd that the matching

condition for S in the transition zone as X →−∞is

S ∼−ΛX, (10.161)

where

Λ =

{(n +2)q

}

1/n

(−B

)

(n+2)/n

. (10.162)

A ﬁnal simpliﬁcation to the transition zone problem results from deﬁning

Π =P +S; (10.163)

652 10 Glaciers and Ice Sheets

to leading order in γ and δ, the transition problem is then

=0,

=−T

n−1

(10.164)

together with the boundary conditions

=W =0onZ =0, (10.165)

B =−(Π +T

(1 −B

) =2T

W =(−˙x

+U)B

on Z =B, X > 0,

(10.166)

and

W =U =0onZ =B

,X<0. (10.167)

The matching conditions to the ice sheet may be summarised as

→−Λ, W →0,T

→−ΛZ as X →−∞, (10.168)

with the ﬂow becoming the resultant pressure gradient driven shear ﬂow at −∞.

Towards the ice shelf, a comparison of orders of magnitude shows ﬁrstly that





1/(n+1)

1, (10.169)

and that in the ice shelf, the transition scaled variables are

S,B ∼

,W∼

,P,T

∼





; (10.170)

note also that the ice shelf time scale νλ is much less than the transition zone time

scale β, so that it is appropriate in the transition zone to assume that the far ﬁeld ice

shelf is at equilibrium, and thus described by (10.145) and (10.146).Bearinginmind

(10.169), it follows from this that suitable matching conditions for the transition

region are

∼−

B, U ∼MX

1/(n+1)

W →0,B∼−

as X →∞,

(10.171)

where

M =



(n +1)







1/(n+1)

, (10.172)

10.2 The Shallow Ice Approximation 653

and the ﬂow becomes an extensional ﬂow as X →∞. It follows from integration

of the continuity equation between B and S that the ice ﬂux to the ice shelf, q

,is

given by

+˙x

. (10.173)

The top surface is deﬁned by

S =(Π +T

Z=0

, (10.174)

and uncouples from the rest of the problem. The extra condition on Z =B, X > 0

in (10.166) should determine B providing ˙x

is known. This is the basic conundrum

of the grounding line determination, since there appears to be no extra condition to

determine ˙x

The resolution of this difﬁculty has not yet been ﬁnally achieved. One might won-

der whether there is an extra condition hiding in the matching conditions (10.168)

or (10.171), but it appears not: the conditions on T

and W as X →−∞imply

the pressure gradient condition, while the condition on U as X →∞implies the

other three. It seems that the answer lies in the additional posing of contact condi-

tions. Speciﬁcally, for the solution in the transition region to have physical sense,

we require that the effective normal stress downwards, −σ

−p

, be positive on

the grounded base, and we require the ice/water interface to be above the submarine

land surface on the ﬂoating shelf base. When written in the current scaled coordi-

nates, these conditions become

B +Π +T

> 0,X<0,

B>B

,X>0.

(10.175)

In addition, we may add to these the condition that at the grounding line, the effec-

tive normal stress is zero, whence

B +Π +T

=0atX =0. (10.176)

Numerical solutions appear to be consistent with the idea that, for any given ˙x

there is a unique value of Λ such that the contact conditions (10.175) and (10.176)

are satisﬁed. If this is true, then (10.162) determines the ice sheet ﬂux q

at the

grounding line as a function of x

(through B

) and ˙x

, and this provides the extra

condition (as well as s →b as x → x

−) for the determination of the grounding

line position.

10.2.8 Marine Ice Sheet Instability

Much of the interest concerning grounding line motion concerns the possible insta-

bility of marine ice sheets. A marine ice sheet is one whose base is below sea level;

the major example in the present day is the West Antarctic Ice Sheet. Marine ice

sheets terminate at grounding lines, from which ice shelves protrude. Depending

on the slope of the submarine surface, they can be susceptible to instability, and it

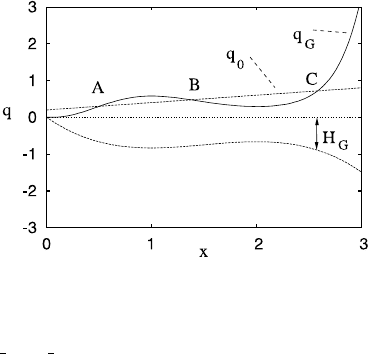
654 10 Glaciers and Ice Sheets

Fig. 10.8 Var ia ti on o f q

(x)] and the equilibrium ﬂux q

=ax for the bottom depth proﬁle

indicated. Equilibria occur for the points of intersection of the two ﬂux curves, with instability

occurring if q



. Thus points A and C are stable, while B is unstable. The particular functions

used are H

=2x −

−

, q

,andq

=0.2(1 +x) (with the divide implicitly being

at x =−1)

has been postulated that ﬂuctuations in sea level, for example, might cause a catas-

trophic retreat of the grounding lines in West Antarctica, and consequent collapse

of the ice sheet.

To understand why this might be so, consider an ice sheet governed by the mass

conservation equation (10.156), and for simplicity (it does not affect the argument),

take the ice ﬂux q =−H

, so that

+a, (10.177)

with boundary conditions

=0atx =0,

H =H

), −H

(H ) at x =x

(10.178)

(note that we retain here the ﬁnite depth of the ice sheet at the grounding line).

(x) represents the depth of the land subsurface below sea level, and we assume

that q

is an increasing function of H , as suggested by (10.162), if Λ is constant.

There is a steady solution H = H

(x); note that since the ice sheet slopes down to

the ice shelf, we have H



)<H



Consider a situation such as that shown in Fig. 10.8, in which the subsurface

slopes upwards for part of the domain. In this case there can be three possible

equilibria, of which the middle one is unstable. The casual argument for this is

the following suggestion: if x

advances, then the ice sheet must deliver a larger

ﬂux q

; however, assuming q



(H ) > 0, then in regions where H



(x) < 0 (i.e., the

bed slopes upwards towards the grounding line), the actual ﬂux delivered is less;

consequently, the ice builds up behind the grounding line, causing its further ad-

vance.

To demonstrate this mathematically, we linearise (10.177) and (10.178) about the

steady state H =H

(x), x

= x

, by putting H = H

(x) + η, x

= x

+γ ;the

10.3 Sliding and Drainage 655

resulting linearised system for η is (eliminating γ )

=η

=0atx =0,

−η

=Kη at x =x

(10.179)

where

K =



) −a



) −H



)

, (10.180)

which has (stable) solutions η = e

−λ

cosλx providing λ tan λx

= K.IfK>0,

these are the only solutions, and the steady state is stable. However, if K<0, the

ﬁrst mode (with λx

π) is replaced by an unstable mode η = e

coshλx,

where λ tanhλx

=−K. Therefore the steady state is unstable precisely if K<0.

Consulting (10.180), and recalling that H



)<H



), it follows that the steady

state is unstable if

<a, (10.181)

as suggested in Fig. 10.8. Question 10.8 generalises this result to the case where

q =−D(H,H

10.3 Sliding and Drainage

The sliding law relates the basal shear stress τ

to the basal sliding velocity u

.The

classical theory, enunciated by Lliboutry, Weertman, Nye, Kamb, and others, con-

siders ice ﬂowing at the base of a glacier over an irregular, bumpy bedrock. The

ice is lubricated at the actual interface by the mechanism of regelation, or melting-

refreezing, which allows a thin ﬁlm (microns thick) to exist at the ice-rock interface,

and allows the ice to slip. The drag is then due to two processes; regelation itself,

and the viscous ﬂow of the ice over the bedrock. Regelation is dominant for small

wavelength roughness, while viscous drag is dominant for large wavelengths, and

early work emphasised the importance of a controlling (intermediate) wavelength

(of several centimetres). More recently, the emphasis has moved away from rege-

lation and has been put more on consideration of the viscous ﬂow, and we do this

here, assuming no normal velocity of the ice as it slides over the bed.

A suitable model for discussion is the ﬂow of a Newtonian ﬂuid over a rough

bedrock of ‘wavelength’ [x] and amplitude [y], given by

y =h

(x) ≡[y]h



[x]



, (10.182)

656 10 Glaciers and Ice Sheets

where y is now the vertical coordinate.

The governing equations for two-

dimensional ﬂow down a slope of angle α are

=0,

=ρ

g sin α +η∇

=−ρ

g cos α +η∇

(10.183)

where η is the viscosity. We suppose that the glacier has a depth of order d, thus

providing a basal shear stress τ

of order [τ ], which drives a shear velocity of order

[u], and these are related by

[τ ]=ρ

gd sin α =

η[u]

. (10.184)

The basal boundary conditions are those of no shear stress and no normal ﬂow, and

take the form

(1 −h

2

) −2τ



1 +h

2

=0, (10.185)

where

=2ηu

,τ

=η(u

), (10.186)

and

v =uh



, (10.187)

both (10.185) and (10.187) being applied at y =h

(x). Note also that the normal

stress is

−σ

p(1 +h

2

) +τ

(1 −h

2

) +2h



1 +h

2

. (10.188)

Because we describe a local ﬂow near the base of the glacier, it is appropriate to

apply matching conditions to the ice ﬂow above. In particular, we require τ

→τ

as y becomes large, and hence

u ∼u

(10.189)

far from the bed.

We non-dimensionalise the equations by scaling

x,y ∼[x],u,v∼[u],τ

=[τ ]τ

∗

=[u]u

∗

p =p

ν[τ ]

(10.190)

where

+ρ

g(y

−y)cos α (10.191)

Because shortly we will use z for the complex variable x +iy.

10.3 Sliding and Drainage 657

is the ice overburden pressure, and y =y

∼d is the ice upper surface (and taken as

locally constant); this leads to the non-dimensional set

=0,

νP

=σ

+∇

νP

=∇

(10.192)

subject to the boundary conditions that

P →0,u∼u

∗

+στ

∗

y as y →∞, (10.193)

and



1 −ν

2



) −4νh



=0,

v =νuh



(10.194)

on the dimensionless bed y =νh (from (10.182)). The corrugation σ and the aspect

ratio ν are deﬁned by

σ =

[x]

,ν=

[y]

[x]

; (10.195)

ν is a measure of the roughness of the bed.

We will assume that both ν and σ are small. In consequence, the dimensionless

basal stress τ

∗

in (10.193) is uncoupled from the problem; however, integration of

the momentum equations over the domain yields an expression for τ

∗

. In dimen-

sional terms, this relation is



ds, (10.196)

where the integral is over a length L of the base y = h

, over which conditions are

taken to be periodic (alternatively, the limit L →∞may be taken).

Evidently, the velocity is uniform to leading order, and therefore we write

u =u

∗

+νU, v =νV, (10.197)

so that the problem reduces to

=0,

+∇

U, (10.198)

=∇

with boundary conditions

U ∼

στ

∗

y as y →∞, (10.199)

and



1 −ν

2



) −4νh



=0,

V =(u

∗

+νU)h



(10.200)

658 10 Glaciers and Ice Sheets

on y =νh. When written in dimensionless terms, the overall force balance (10.196)

takes the form (with L now being dimensionless)

στ

∗







1 +ν

2





1 −ν

2



+2νh



)





1 +ν

2

(10.201)

It is fairly clear from (10.201) that there is a distinguished limit σ ∼ν

, which corre-

sponds to the situation where sliding is comparable to shearing, and it is convenient

to adopt this limit as an example. We introduce a stream function ψ via

U =ψ

,V=−ψ

; (10.202)

then letting ν →0 with σ ∼ν

, we derive the reduced model

=∇

=−∇

(10.203)

together with the boundary conditions

P,ψ →0asy →∞,

ψ =−u

∗

h(x), ψ

−ψ

=0ony =0.

(10.204)

The shear stress is determined by (10.201), whence to leading order (e.g., if h is

periodic with period 2π)

στ

∗

2π



2π

(P +2ψ

y=0



dx; (10.205)

more generally a spatial average would be used. Since the expression in brackets in

(10.205) is simply (minus) the normal stress, it is therefore also equal to the scaled

water pressure in the lubricating ﬁlm, which from (10.190) can be written in the

form

P +2ψ

=−N

∗

σ(p

−p

)

ν[τ ]

. (10.206)

The quantity N

∗

is the dimensionless effective pressure at the bed. We come back

to this below.

A nice way to solve this problem is via complex variable theory. We deﬁne the

complex variable z =x +iy, and note that Eqs. (10.203) are the Cauchy–Riemann

equations for the analytic function P +i∇

ψ. Consequently, ψ satisﬁes the bihar-

monic equation, which has the general solution

ψ =(¯z −z)f (z) −B(z) +(cc), (10.207)

where f and B are analytic functions and (cc) denotes the complex conjugate, as

does the overbar. The zero stress condition (10.204) requires f =−



, and also

B →0asz →∞(with Im z>0), and the last condition is then

B +

B =u

∗

h on Im z =0. (10.208)

10.3 Sliding and Drainage 659

If h is periodic, with a Fourier series

h =

∞



−∞

ikx

, (10.209)

then B is simply given by

B =u

∗

∞



ikz

(10.210)

(we can assume a

=0, i.e., the mean of h is zero). However, it is also convenient

to formulate this problem as a Hilbert problem. We deﬁne L(z) =B



(z), which is

analytic in Im z>0, and then L(z) =



(¯z) is analytic in Im z<0. From (10.207),

∇

ψ = 4ψ

z¯z

=−2(L +

L), and therefore P +i∇

ψ + 4iL = P + 2i(L −

L) is

analytic; since this last expression is real, it is constant and thus zero, since it tends

to zero as z →∞. Applying the boundary conditions at Im z = 0, and using the

usual notation for the values on either side of the real axis, it follows that

−

∗



−L

−

iP,

(10.211)

which relate the values either side of Im z = 0. From (10.207), we have ψ

i(ψ

− ψ

¯z¯z

) =

i(z −¯z)(B



− B



), and thus ψ

y=0

= 0; it follows that P =

−N

∗

on y = 0, and the drag (i.e., the sliding law) is then computed (for a 2π-

periodic h)as

στ

∗

iπ



2π

−L

−



dx; (10.212)

evaluating the integral, we ﬁnd

στ

∗

=4u

∗

∞



. (10.213)

For a linear model such as this, τ

∗

and thus τ

is necessarily proportional to u

∗

and

thus u

. For Glen’s ﬂow law, the slip coefﬁcient multiplying τ

∗

becomes

n+1

.The

problem cannot be solved exactly, but variational principles can be used to estimate

a sliding law of the form

≈Ru

1/n

. (10.214)

Weertman’s original sliding law drew a balance between (10.214) and the linear

dependence due to regelation, and the heuristic ‘Weertman’s law’ τ

∝ u

1/m

, with

m ≈

(n +1) is often used.

Simplistic sliding laws such as the above have been superseded by the inclusion

of cavitation. When the ﬁlm pressure behind a bump decreases to a value lower

than the water pressure in the local subglacial drainage system, a cavity must form,