Fowler A. Mathematical Geoscience
Подождите немного. Документ загружается.


780 11 Jökulhlaups
and ≈2,900 m
2
for Fig. 11.8), which imply maximum channel radii in the region
of 20 m and 43 m, respectively, it is pertinent to wonder whether the assumption of
semi-circular cross section is likely to be correct.
We can give some plausibility arguments to suggest why a circular shape is
adopted. For ‘weak’ floods in which the channel effective pressure is always pos-
itive, channel closure is that of a more viscous ‘fluid’ pushing back a less viscous
one. For this situation, viscous fingering does not occur, and a circularly deforming
boundary is stable. Further arguments in this direction are that, since the ice pres-
sure is larger at the glacier bed, the contracting effective stress is larger there: this
mitigates against wider channels, while taller channels are not favoured because of
the consequent increased lateral melting.
None of these arguments work for ‘strong’ (flotation driven) floods, which as we
have discussed, propagate as viscous fractures at the tip, and in which the channels
must therefore be wide (Jóhannesson 2002a, 2002b).
Temperature The assumption of equilibrium temperature (and thus the removal
of θ from the Nye model) seems rather unfortunate, and it would seem that at least it
would affect the flood dynamics in a quantitative manner. Let us therefore reconsider
the energy equation. Neglecting ε in (11.17), we have
Q
∂θ
∂x
=Q
ˆ
Φ −m, (11.160)
where we write the hydraulic gradient as
ˆ
Φ =Φ +
∂N
∂X
(11.161)
(here x =δX). Since
Q|Q|=S
8/3
ˆ
Φ, m ≈
θ
γ
|Q|
S
1/2
0.8
, (11.162)
the temperature equation simplifies to
∂θ
∂x
=
ˆ
Φ −
θ
λ
, (11.163)
where
λ =
γ |Q|
0.5
sgnQ
|
ˆ
Φ|
0.15
. (11.164)
Our simplification of the Nye model to the form (11.42) was based on the neglect
of the advective term in (11.163). As we stated, between floods this seems entirely
reasonable, since in equilibrium θ ≈ λ
ˆ
Φ 1. During floods, if we take
ˆ
Φ to be
constant, we see that the advective term θ
x
= exp(−x/λ), and in fact this is small
away from the lake, since for weak floods, we have computed the peak Q ∼10
−2
,
thus λ ∼ 0.1, and θ
x
∼ 10
−4
. However, the neglect of the advective term is inac-
curate near the lake where x =δX, and in this region the equilibrium assumption
leads to the approximation for the advective term
θ
x
≈
γ
√
Q
δ
ˆ
Φ
0.85
, (11.165)

11.8 Notes and References 781
where the prime denotes differentiation of
ˆ
Φ
0.85
with respect to X: γ and δ are de-
fined in (11.18), with typical values given in (11.21). This term is of order γ
√
Q/δ,
and becomes significant at peak discharge. Its effect on the melt rate m which ap-
pears in the channel closure equation (11.17)
1
is to replace m =
ˆ
ΦQ by
m ≈Q[
ˆ
Φ −θ
x
] (11.166)
(see (11.160)). Inspection of our numerical results shows that S
X
< 0atthelake
at peak discharge, and thus (since
ˆ
Φ = Q
2
/S
8/3
),
ˆ
Φ
> 0, and thus θ
x
> 0. The
effect of including temperature adjustment should therefore be to reduce the peak
discharge.
This assumes the lake temperature is essentially equal to the freezing tempera-
ture, i.e., θ = 0atx = 0. If the lake is superheated, as might be the case following
an eruption, then we expect θ
x
< 0, and the peak discharge will be enhanced. As we
have seen, the floods may be rather different in this case. In particular, we associate
warm water temperature with rapid lake filling, and a likely strong flood propagating
down glacier as a wide fracture channel. Now consideration of the empirical heat
transfer relation (11.5) shows that the term raised to the power 0.8 is essentially
the Reynolds number for a semi-circular channel. For a wide channel, the relevant
length scale is the channel depth, and this implies that to use (11.5) for a wide chan-
nel, we should multiply the constant a
DB
by (h/w)
0.4
, where h is channel depth and
w is channel width. For a wide channel, this cause an increase in γ , which enhances
the importance of the thermal advective term.
However, our problem is really the opposite of this. According to (11.163) and
(11.164), the exit temperature of the water ought to be θ ∼ γ
√
Q. For a peak
discharge of Q = 0.033 (corresponding to 6,000 m
3
s
−1
) and with γ ∼ 2.5asin
(11.21), we have θ ∼ 0.45 corresponding to an exit temperature of 1.6°, using the
scale for θ
0
in (11.20). This is about thirty times higher than is observed (Clarke
2003), suggesting that heat transfer should be much more efficient than that given
by the Dittus–Boelter relation assumed by Nye (1976). Two possible reasons are
that the measurements used in establishing the Dittus–Boelter relation were done at
Reynolds numbers between 10
4
and 10
5
, which is two or three orders of magnitude
less than our situation. It may simply be that the heat transfer parameterisation is
not very accurate. Possibly more likely is that other physical processes contribute to
a larger effective heat transfer; for example, mechanical erosion of ice by the turbu-
lent, sediment-laden flow. In either event, it seems there are good reasons to suppose
that a practical value of γ may be much smaller than given in (11.21).
It has to be said in any case that inclusion of the temperature equation in the form
(11.163) is not a straightforward addition to the numerical problem of solving the
Nye equations. The reason for this is that when X
∗
> 0, the θ equation (11.163)
must be solved in a direction away from the seal: that is, we prescribe (or in fact
require) θ =0atX =X
∗
, and must solve for θ by stepping backwards into X<X
∗
and forwards into X>X
∗
. This is not an insurmountable problem, but it is at least
awkward, because of the singularity at X = X
∗
. A reasonable alternative would
be to ignore advection if X
∗
< 0, and only solve (11.163)ifX
∗
> 0. If the lake
temperature is positive, this gives a discontinuity in θ at flood initiation, and this
would cause further numerical awkwardness.
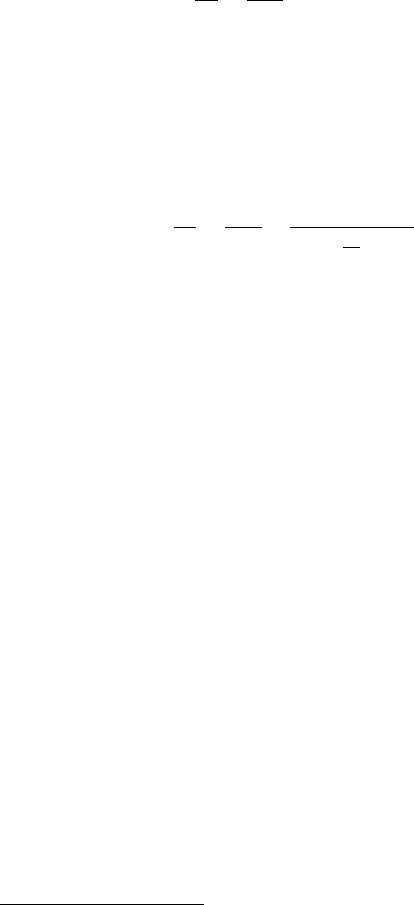
782 11 Jökulhlaups
Snout Closure and Open Channel Flow If we reconsider the channel closure
equation
∂S
∂t
=
|Q|
3
S
8/3
−S|N|
n−1
N, (11.167)
it is clear that the boundary condition N =0 at the snout x =1 is problematic, since
it predicts indefinite opening of the channel. The problem is that the closure rate
term is based on Nye’s (1953) calculation of closure of a cylindrical borehole in an
infinite medium, which becomes increasingly irrelevant at the snout. It is simple to
modify Nye’s analysis to consider the effect of a stress-free outer boundary at radius
R
f
, and the effect of this is to modify the closure term in (11.167) so that the closure
equation becomes
∂S
∂t
=
|Q|
3
S
8/3
−
S|N|
n−1
N
1 −
S
S
f
1/n
n
, (11.168)
where S
f
=πR
2
f
. This limits the growth of S because S ≤S
f
everywhere; (11.168)
applies if S<S
f
, and is replaced by the condition S =S
f
if S ≥S
f
. In practice we
might take S
f
proportional to ice depth (perhaps to some power).
A further complication is that in practice the channel may reach atmospheric
pressure at some distance up stream from the snout. In this case, the location of the
position where N =0 is a free boundary, with the extra condition being that the flux
becomes equal to the open channel value.
Inertia Terms One of the subtleties that Spring and Hutter introduced was the
inertial acceleration terms in the water momentum equation. Later, Clarke (2003)
found a way to solve this formulation of the problem numerically. The inertial terms,
when scaled, are multiplied by a form of Froude number squared, but one computed
with the ice depth, not the channel depth (see Question 11.5). In general, this term
is small and can be safely neglected. Inclusion of inertia terms simply introduces
complication without any advantage.
Channel Roughness In his seminal paper, Nye (1976) used a Manning roughness
of n
= 0.12 m
−1/3
s in order to fit the rising limb of the 1972 Grímsvötn hydro-
graph. This represents a very rough channel, and Clarke (2003) thought that such a
value was too high. Nye only used this to fit the rising limb, and did not otherwise
solve his model. In fact, it is perfectly possible to fit the whole 1972 hydrograph
using lower choices of roughness; for example, Fowler (2009) fitted the 1972 peak
discharge and duration using values A
L
= 10 km
2
(cf. Björnsson 1992, Fig. 2)
9
and n
= 0.04 m
−1/3
s: see also Question 11.7. On the other hand, we might well
suppose that a sediment-laden torrent at Reynolds number 10
8
might well be very
rough.
9
Our previous choice of A
L
= 30 km
2
(after (11.30)) corresponded to the maximum area before
1940, since when the lake area has declined; 10 km
2
is approximately the minimum lake area in
1972. A
L
is an approximately linearly increasing function of lake level, and hence a decreasing
function (see (11.25)) of N
0
.

11.8 Notes and References 783
The Viscous Beam Thin films abound in applied mathematics, having applica-
tions in, for example, glass blowing, foam drainage, and coating flows, and in the
first two of these, where there is no shear stress applied at the upper and lower sur-
faces, the problem is essentially the same as that describing ice shelves, or where
there is a load, ice cauldrons. An entry into this literature is through the papers by
Howell (1996) and Teichman and Mahadevan (2003), for example.
Floods from Ice Sheets The description of the Channelled Scablands of Eastern
Washington State and their origin by massive floodwaters is due to Bretz (1923,
1969). Initially the floods were associated with glacial meltwater, and later with the
ice-dammed glacial Lake Missoula. The sequential nature of the Missoula floods is
described by Waitt (1984), for example.
The 8,200 year cold event is discussed by Alley et al. (1997), and a theoretical
discussion is given by Clarke et al. (2004). Commentary on this paper by Sharpe
(2005) and the authors’ reply (Clarke et al. 2005) focusses on the related work by
John Shaw and his co-workers (e.g., Shaw 1983; Shaw et al. 1989). Shaw’s central
thesis is that drumlins (see Chap. 10) were formed subglacially by flowing meltwa-
ter. The analogy with fluvial erosional forms then dictates high Reynolds number
flows, and consequently that such erosion could only have occurred in huge floods
(so the argument goes). Shaw and his followers have been somewhat messianic in
their pursuit of this thesis, but it has to be said that many of the central pillars of the
argument are coming to be accepted: the existence of subglacial lakes, the existence
of pro- and subglacial floods. Like a Shakespearean tragedy, the single flaw in the
argument stems from the unnecessary assumption that because drumlins look ‘like’
fluvial erosion forms, they must be such forms. Most scientists are put off the Shaw
theory because of the apparently unrealistic constraints which the theory seeks to
impose: vast lakes, enormous floods, beyond the ability of a reputable theory to
explain as being physically possible.
Sub-Antarctic lakes are described by Siegert et al. (1996), for example, who give
an inventory of such lakes. A more recent review is by Siegert (2005). The largest
and best known is Lake Vostok (Siegert et al. 2001), which has an approximate vol-
ume of 5,000 km
3
. Lake Vostok may ‘drain’ by basal freeze on, which currently
appears to remove the lake water. For the sorts of subglacial floods described by
Denton and Sugden (2005) (see also Sugden and Denton 2004
10
), some such huge
body of water must drain to the coast, although whether this is possible for Vostok
is not known. Goodwin (1988) describes a jökulhlaup of six months duration ob-
served near the coast in East Antarctica. More recently, Wingham et al. (2006)have
observed small scale floods of a subglacial lake in the Adventure Trough of East
Antarctica. Erlingsson (2006) raises the possibility of a Vostok jökulhlaup.
Dansgaard–Oeschger events were already discussed in Sect. 2.5.5. Ganopolski
and Rahmstorf (2001) provide the model result that freshwater flux oscillations of
magnitude 0.1 Sv (10
5
m
3
s
−1
) can cause switching of the circulatory state. Similar
10
Note: in Fig. 1 of this paper, the two marks of 130° E should both read 163° E (David Sugden,
private communication).

784 11 Jökulhlaups
results are given by Stocker and Wright (1991). Alley et al. (2001) and Ganopolski
and Rahmstorf (2002) suggest that a very weak periodicity may be amplified to
produce the 1,500 year cycle by means of stochastic resonance.
Mars An elegant, if slightly manic, discussion of recent theories about Mars is
the semi-popular book by Kargel (2004). The list of contents is off-putting, but the
material is stimulating, and there are many excellent photographs from the vari-
ous Mars orbiting spacecraft. The literature on Mars is mostly based around these
images and their interpretation. An early paper on massive floods is by Baker and
Milton (1974), and a more recent review is that by Baker (2001). Two contrasting
views (CO
2
or water?) are described by Hoffman (2000) and Coleman (2003), and
the possibility of jökulhalups on Mars, possibly associated with sub-ice volcanoes,
is considered by Chapman et al. (2003).
11.9 Exercises
11.1 In the absence of lake refilling at the inlet, a suitable boundary condition for
(11.17)ats =0isQ =0. Assuming Q
0
is chosen so that Ω =1 (why?), find
typical values of the dimensionless parameters, and hence derive an approx-
imate ordinary differential equation for N describing steady state drainage.
Show further that, if δ is small, a further simplification is possible, and in this
case derive an approximate drainage law in the form N =cQ
ν
, and give ex-
plicit expressions and typical values for c and ν. The approximation δ →0is
a singular perturbation; where does if fail, why, and what is the resolution?
11.2 Suppose the hydraulic gradient near X =0 is given by
Φ =1 −ae
−bX
,
and N and Q are determined on 0 <X<∞ by
Φ +
∂N
∂X
=N sgnQ,
Q =ω(X −X
∗
),
with
N →1asX →∞,
N =N
L
on X =0,
˙
N
L
=−(ν +ωX
∗
),
where ω and ν are small. Show that
N
L
(0) =2e
X
∗
−
1 +
a
b −1
+
2a
b
2
−1
e
−(b−1)X
∗
,
and deduce that the seal is weak (seal breaking occurs when the lake level is
below flotation: N
L
(0)>0) if a<b+1.
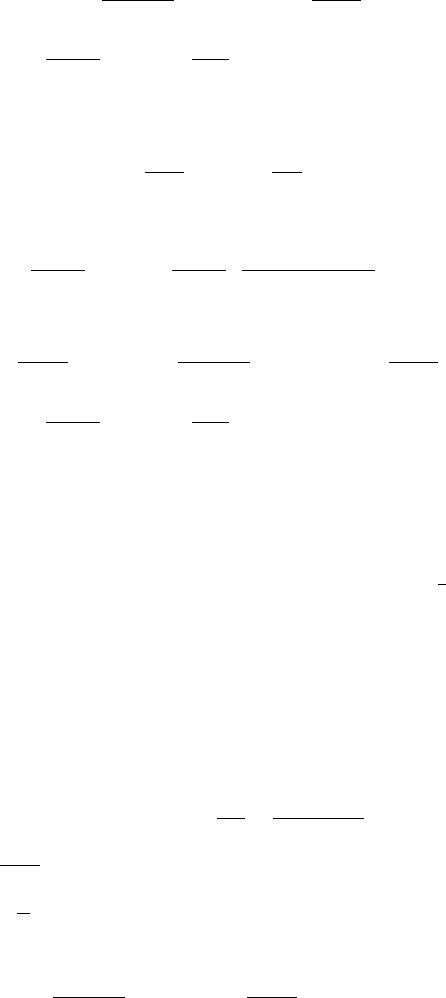
11.9 Exercises 785
11.3 Use the relations
S
0
=
fρ
w
gQ
2
0
Φ
0
3/8
,m
0
=
Φ
0
Q
0
L
,
Φ
0
=
ρ
w
gh
0
l
,t
0
=
ρ
i
S
0
m
0
,N
0
=(Kt
0
)
−1/n
,
to find explicit relations for the scales S
0
, m
0
, etc. in terms of Q
0
, and hence
show that the parameters
ε =
S
0
l
t
0
Q
0
,δ=
N
0
Φ
0
l
are given by
ε =
ρ
w
gh
0
ρ
i
L
,δ=
1
ρ
w
gh
0
Q
1/4
0
Φ
11/8
0
ρ
i
KL(fρ
w
g)
3/8
1/n
.
11.4 Use the definitions
Q
0
=
A
L
N
0
ρ
w
gt
0
,S
0
=
fρ
w
gQ
2
0
Φ
0
3/8
,m
0
=
Φ
0
Q
0
L
,
Φ
0
=
ρ
w
gh
0
l
,t
0
=
ρ
i
S
0
m
0
,N
0
=(Kt
0
)
−1/n
,
to estimate values for the peak discharge Q
max
∼Q
0
and the total discharge
V
max
∼ Q
0
t
0
(assuming A
L
is constant). By varying in turn A
L
, K, f and
Φ
0
, show that
Q
max
∝V
b
max
,
and compare the values of b with the Clague–Mathews result b =
2
3
, or that
of Björnsson, b =1.84.
[The Clague and Mathews (1973) peak discharge/volume relationship is
a venerable curiosity of subglacial hydrology, and appears to have no simple
explanation. Other studies include those by Björnsson (1992), Walder and
COsta (1996), and Ng and Björnsson (2003), the last of which provides a
detailed analytic investigation.]
11.5 The momentum equation in the model for subglacial drainage is modified to
include inertial acceleration terms, thus
ρ
w
(u
t
+uu
x
) =Φ +
∂N
∂x
−
fρ
w
gQ|Q|
S
8/3
,
where Φ =
ρ
w
gd
i
l
is the basic hydraulic gradient, d
i
is ice depth, l is glacier
length, N is the effective pressure, Q is volume flux, S is cross-sectional
area, and u =
Q
S
is the mean velocity. By scaling the variables as
Φ =Φ
0
Φ
∗
,N∼N
0
,x∼l, Q ∼Q
0
,
S ∼
fρ
w
gQ
2
0
Φ
0
3/8
,t∼
ρ
i
LS
0
Φ
0
Q
0
,

786 11 Jökulhlaups
show that the dimensionless form of this equation can be written as
F
2
(εu
t
+uu
x
) =Φ
∗
+δ
∂N
∂x
−
Q|Q|
S
8/3
,
where
δ =
N
0
ρ
w
gd
i
,ε=
ρ
w
gd
i
ρ
i
L
,F
2
=
u
2
0
gd
i
,
and u
0
=
Q
0
S
0
. Show that, if Q
0
= 10
5
m
3
s
−1
, S
0
= 10
4
m
2
, g = 10 m s
−2
and d
i
=500 m, then F
2
∼0.02, and explain why more generally the accel-
eration terms can be neglected. What complications do they cause if they are
included?
11.6 In an approximate model for the channel effective pressure between floods,
N satisfies the Riccati equation
Φ(X) +
∂N
∂X
=N
2
sgn(X −X
∗
),
with boundary conditions
N →1asX →∞,
N =N
L
at X =0,
where we assume Φ(∞) =1.
Assume that
Φ =1 −ae
−bX
,
and use appropriate substitutions in X ≶ X
∗
of the form N = w
/cw to
reduce the model to a pair of linear equations for w. Hence show that for
X>X
∗
,
N =−
v
v
,v=J
ν
λe
−X/ν
,
where
λ =
2
√
a
b
,ν=
2
b
,
and for X<X
∗
,
N =
w
w
,w= J
iν
iλe
−X/ν
+αY
iν
iλe
−X/ν
,
where α must be chosen so that N is continuous at X
∗
.
Hence show that
N
L
(0) =
λJ
ν
(λ)
νJ
ν
(λ)
,
and deduce that the seal is weak if
J
ν
(λ)
J
ν
(λ)
> 0, and thus if
a<a
2
=
1
2
bj
(2/b),1
2
,
where j
ν,1
is the first zero of J
ν
(z).

11.9 Exercises 787
Use tables to evaluate j
ν,1
for ν =
1
2
, 1, 2, 3, 4, 5, and compare the conse-
quent values of a
2
for b<4 with those obtained from the asymptotic result
j
ν,1
≈ ν + 0.81ν
1/3
when ν 1, and deduce that the small b approxima-
tion is accurate in this range. By plotting the results numerically, show that a
useful approximation to a
2
is then
a
2
≈1.2 +b,
for b<4.
An even better approximate model is to take
Φ +
∂N
∂X
=
N
2
σ
2
sgn(X −X
∗
),
where σ = ω
1/11
≈ 0.44 (since Q ∼ ω)forω = 1.2 × 10
−4
. In this case,
modify the analysis above to show that a seal is weak if
a<a
2
=
1
2
σbj
(2/σ b),1
2
,
and deduce that
a
2
≈1.2 +0.44b
for b<9.
11.7 The dimensionless, reduced Nye model for jökulhlaups depends on dimen-
sionless parameters ω =δΩ and ν defined by
ω =
M
Φ
0
Q
0
Φ
11/8
0
Q
1/4
0
ρ
i
KL(fρ
w
g)
3/8
1/n
,ν=
m
L
Q
0
,
and the dimensional results depend on the volume flux scale Q
0
and time
scale t
0
defined by
t
0
=
ρ
i
L
Φ
0
(fρ
w
g)
3/8
Q
1/4
0
,
Q
0
=
A
L
ρ
w
g
n
1
K
Φ
0
fρ
w
g
3/8
Φ
0
ρ
i
L
n+1
4/(3n−1)
.
The periodic solutions therefore have dimensional period
P =
t
0
ν
P
∗
,
and the floods have peak discharge
Q
max
=Q
0
Q
∗
and duration
t
F
=t
0
t
∗
.

788 11 Jökulhlaups
In general, the starred quantities are functions of ω and ν, but let us assume
they depend only on the quantity
α =
ω
4n/(4n−1)
ν
=
1
m
L
M
Φ
0
m
L
4n/(4n−1)
Φ
11/8
0
ρ
i
KL(fρ
w
g)
3/8
4/(4n−1)
.
Suppose that a particular numerical solution, with particular choices for
the scales and parameters (and in particular f =f
n
, A
L
=A
n
and m
L
=m
n
),
produces floods of (dimensional) duration t
n
, peak discharge Q
n
and with
period P
n
, whereas the actual observed floods have corresponding quantities
t
a
, Q
a
and P
a
. Show how, by choosing new values f = f
a
, A
L
= A
a
and
m
L
=m
a
, the numerical solution can be made to fit the data, and give explicit
expressions for the ratios
f
a
f
n
,
A
a
A
n
and
m
a
m
n
.
11.8 The Nye model for jökulhlaups can be reduced to the system
∂S
∂t
=
|Q|
3
S
8/3
−S|N|
n−1
N,
Q =ω(X −X
∗
),
Φ +
∂N
∂X
=
Q|Q|
S
8/3
,
with the boundary conditions that
∂N
∂t
(0,t) = Q(0,t)−ν,
∂N
∂X
→0asX →∞,
assuming that the effect of thermal advection is ignored.
Suppose that ω ∼ν 1. Show that between floods, the variables can be
rescaled (explaining how) so that the equations take the form
β
∂s
∂T
=
|q|
3
s
8/3
−|Π |
n−1
Π,
q =ξ −ξ
∗
,
Φ +Π
ξ
=
|q|q
s
8/3
,
subject to
Π
T
=−1 +αq on ξ =0,
Π
ξ
→0asξ →∞,
where
α =
ω
4n/(4n−1)
ν
,β=
ν
ω
(n+1)/(4n−1)
,
and show that for values of ω, ν ∼10
−3
, β 1butα =O(1) (e.g., if n =3).
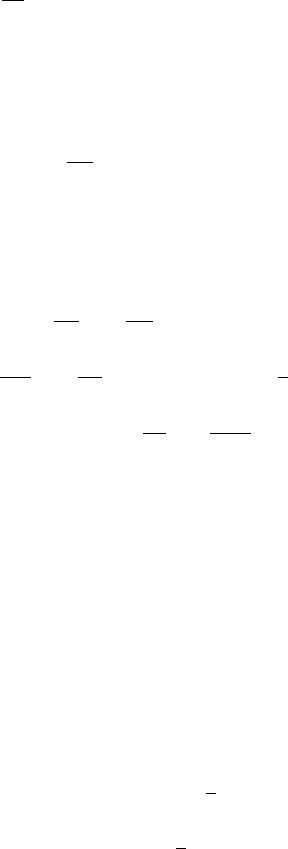
11.9 Exercises 789
Show that if β is put to zero, then the Nye model between floods (when
ξ
∗
> 0 and Π>0) can be solved by computing the solution to the system
d
dξ
|ξ −ξ
∗
|
1/4n
R
=R
8n/11
sgn(ξ −ξ
∗
) −Φ(ξ),
subject to
R →Φ
11/8n
∞
as ξ →∞
and
d
dT
ξ
∗(1/4n)
R
ξ=0
=−1 −αξ
∗
.
Consider and explain the difficulties in solving this problem numerically.
Explain why this approximation can break down if ν ω.
11.9 The vertically integrated dimensionless viscous ice beam equations are given
by
2
∂T
∂x
+ν
2
∂U
∂x
=γβNh
x
+β(s −h)s
x
,
∂M
∂x
−ν
2
∂L
∂x
+S =−γβNhh
x
−
1
2
β
s
2
−h
2
s
x
,
∂S
∂x
=−
γβN
ν
2
,
where M, S, T , U and L are defined by
M =−
s
h
2zτ
1
dz, S =
s
h
τ
3
dz, T =
s
h
τ
1
dz,
U =
s
h
σ
3
dz, L =
s
h
zσ
3
dz,
s(x,t) is the ice surface elevation, h(x, t) is the lake roof, and p + τ
1
=
−ν
2
σ
3
.
Show that if
−p +τ
1
=β(s −z), τ
3
=0
on x =x
±
, which denote the subglacial lake margins, then
2T +ν
2
U =
1
2
β(s −h)
2
,
−M +ν
2
L =
1
6
β(s −h)
2
(s +2h),
S =0,
at x =x
±
. Show that
x
+
x
−
Ndξ=0,
