Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.

6 Applications to Nonlinear PDEs in IR
N
293
u(x , t)
r =|x|
t
1
0
t
2
t
4
T
r
0
s
−
(t)
s
+
(t)
t
1
< t
2
< T < t
4
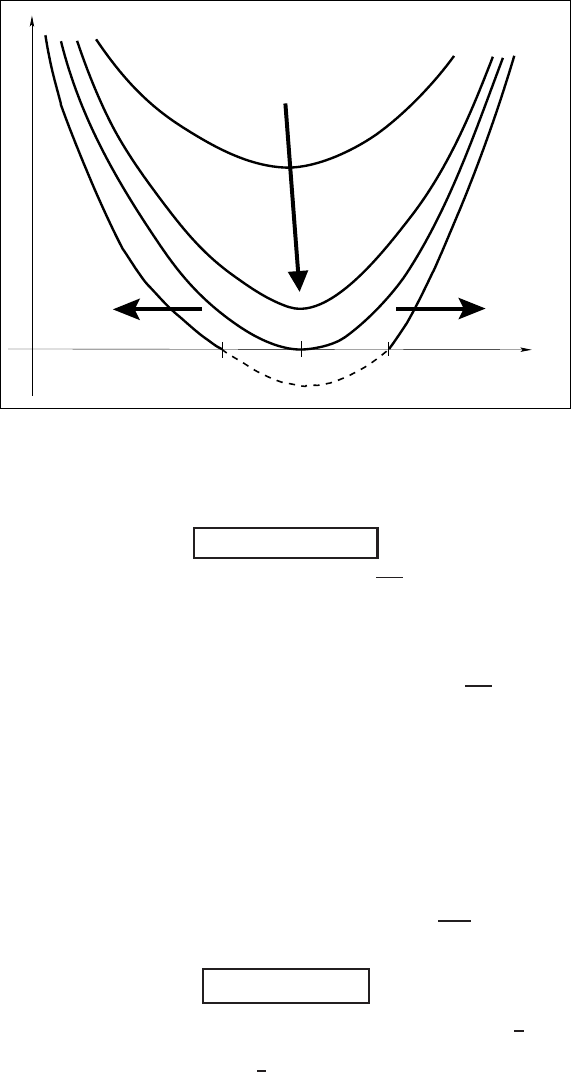
Figure 6.1 Quenching at t = T of positive solutions (6.55). For t > T , there appear two
interfaces and an FBP should be properly posed.
yields the PDE
u
t
= F[u] + au + b.
There exist solutions v(x, t) =
C
1
(t) + C
2
(t)|x |
2
−
N+2
2
of (6.56), where
C
1
= 2NC
2
1
C
2
+ aC
1
+ b,
C
2
= 2NC
1
C
2
2
+ aC
2
,
which are not new. By the true pressure transformation v = u
−
N+2
4
, (6.56) reduces
to a quadratic PDE, which, in general, possesses a wider class of exact solutions on
W
r
3
= L{1, |x |
2
, |x |
4
}, where Proposition 6.24 applies.
6.3 On the remarkable operator in IR
2
Consider the following remarkable quadratic operator:
F
rem
[u] = uu −|∇u|
2
on the plane (x, y) ∈ IR
2
, (6.57)
which, according to (6.38), has the critical parameter γ =−
N+2
4
=−1. The corre-
sponding quadratic parabolic equation
u
t
= uu −|∇u|
2
(6.58)
is transformed into the fast diffusion PDE by the pressure change v =
1
u
,
v
t
=∇·
1
v
∇v
≡ ln|v|. (6.59)
© 2007 by Taylor & Francis Group, LLC
294 Exact Solutions and Invariant Subspaces
This PDE arises as a model for long van der Waals interactions in thin films of
a fluid spreading on a solid surface if fourth-order effects are neglected [249, 54]
(cf. Section 3.1). It also represents (see [278] and, e.g., [577]) the evolution of the
conformallyequivalent metric g
i, j
ds
2
= v(dx
2
+dy
2
)
under the Ricci flow which
evolves a general metric ds
2
= g
i, j
dx
i
dy
j
by its Ricci curvature R
i, j
by the PDE
∂
∂t
g
i, j
=−2R
i, j
. (6.60)
In the present case, the conformal metric g
i, j
= v I
i, j
has scalar curvature R =
−
1
v
lnv and R
i, j
=
1
2
Rg
i, j
,whereR(x , t) satisfies the semilinear heat equation
R
t
= R + R
2
, (6.61)
which admit solutions blowing-up as t → T
−
< ∞. As a principal feature, note
that (6.60) is a system of second-order nonlinear parabolic equations which obey the
Maximum Principle (similar to (6.61)). In Hamilton [278], it was established that,
for a given compact 3D manifold with initially positive Ricci curvature, after scal-
ing, the Ricci flow (6.60) evolves to a metric of positive constant curvature (so the
manifold is diffeomorphic to the sphere S
3
). A crucial part of Hamilton’sanalysis
is proving that solutions R(x, t)>0 of (6.61), after scaling, form a symmetric in x
blow-up singularity as t → T . The phenomenon of symmetrizationclose to blow-up
time is a fundamental property of many nonlinear evolution PDEs. In the previous
chapters, this has been checked for a number of parabolic equations admitting ex-
act solution on invariant subspaces. New refined estimates of solutions of equations
(6.60) and (6.61) (and, implicitly, (6.58) and (6.59)), including a monotonicity for-
mula [97, p. 254], are a core of Perel’man’s approach to the Poincar´e Conjecture (a
closed connected 3D manifold is homeomorphic to S
3
; see [97] for history, refer-
ences, and recent development).
It is known [10, Sect. 10.7] that the symmetry Lie algebra of equation (6.59) con-
tains an infinite-dimensionalsubalgebra generated by operators
X = ξ
1
∂
∂x
+ ξ
2
∂
∂y
− 2ξ
1x
v
∂
∂v
, (6.62)
where ξ
1
(x , y) and ξ
2
(x , y) are arbitrary harmonic conjugate functions, i.e., satisfy-
ing the Cauchy–Riemann conditions
ξ
1x
= ξ
2y
,ξ
1y
=−ξ
2x
.
The existence of this algebra is connected with the invarianceof equation (6.59) with
respect to the transformation
¯x = η(x, y), ¯y = δ(x, y), ¯v =
v
(η
x
)
2
+(η
y
)
2
, (6.63)
where η and δ are arbitrary independent harmonic conjugate functions,
δ
x
= η
y
,δ
y
=−η
x
(δ
x
η
y
− δ
y
η
x
= 0). (6.64)
The first two formulae (6.63) define a group of conformal transformations of the
(x , y)-plane. Imposing in addition the conditions
δ
x
=
ξ
1
ξ
2
1
+ξ
2
2
,δ
y
=
ξ
2
ξ
2
1
+ξ
2
2
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
295
yields that, in the variables (6.63), the operator (6.62) takes the form
¯
X = ∂/∂ ¯y
which corresponds to translations in ¯y.
Hence, for equation (6.58), we obtain the transformation
¯x = η(x, y), ¯y = δ(x, y), ¯u =
(η
x
)
2
+ (η
y
)
2
u, (6.65)
leaving this equation invariant. Applying the transformation (6.65) to a solution u =
f (x, y, t) of (6.58) yields an infinite family of solutions,
u(x , y, t) =
1
(η
x
)
2
+(η
y
)
2
f (η(x , y), δ(x, y), t), (6.66)
containing a pair of harmonic conjugate functions. In particular, taking solution u =
f (x, t) independent of y, i.e., satisfying the 1D equation
u
t
= uu
xx
− (u
x
)
2
,
yields the solution
u(x , y, t) =
1
(η
x
)
2
+(η
y
)
2
f (η(x, y), t) (6.67)
of the 2D equation (6.58).
Thus, operator (6.57) is “doubly critical”, since, in addition to the property in
Proposition 6.24, the associated parabolic (and also elliptic) PDE admits an infinite-
dimensional Lie algebra of symmetries. This is a rare situation for nonlinear equa-
tions that allows us to discuss new aspects concerning the structure of invariant sub-
spaces and nonlinear separation of variables.
6.3.1 Polynomial subspaces
Proposition 6.37
Operator
(6.57)
preserves the 9D subspace
W
9
= L
1, x , y, x
2
, xy, y
2
, xr
2
, yr
2
, r
4
r
2
= x
2
+ y
2
. (6.68)
This subspace has larger dimension than most other quadratic operatorsstudied so
far. Subspace (6.68) is an extension for N = 2 of that given in Proposition 6.26.
Example 6.38 (Fast diffusion equation and remarkable operators) The fast dif-
fusion equation with a quadratic reaction-absorption term
v
t
=∇·
1
v
∇v
− av
2
− bv (6.69)
by the pressure change v =
1
u
reduces to
u
t
= F
rem
[u] + a + bu in IR
2
× IR
+
. (6.70)
There exist solutions, which are more general than (6.46),
u(x , t) = C + d
1
x + d
2
y + a
1
x
2
+ a
2
xy + a
3
y
2
+ e
1
xr
2
+ e
2
yr
2
+ Gr
4
, (6.71)
© 2007 by Taylor & Francis Group, LLC
296 Exact Solutions and Invariant Subspaces
where the expansion coefficients satisfy the DS
C
= [2(a
1
+ a
3
) + b]C − d
2
1
− d
2
2
+ a,
d
1
= [2(a
3
− a
1
) + b]d
1
− 2a
2
d
2
+ 8Ce
1
,
d
2
= [2(a
1
− a
3
) + b]d
2
− 2a
2
d
1
+ 8Ce
2
,
a
1
= [2(a
3
− a
1
) + b]a
1
− a
2
2
+ 2d
1
e
1
− 2d
2
e
2
+ 16CG,
a
2
= [−2(a
1
+ a
3
) + b]a
2
+ 4d
2
e
1
+ 4d
1
e
2
,
a
3
= [2(a
1
− a
3
) + b]a
3
− a
2
2
− 2d
1
e
1
+ 2d
2
e
2
+ 16CG,
e
1
= [2(a
3
− a
1
) + b]e
1
− 2a
2
e
2
+ 8Gd
1
,
e
2
= [2(a
1
− a
3
) + b]e
2
− 2a
2
e
1
+ 8Gd
2
,
G
= [2(a
1
+ a
3
) + b]G − e
2
1
− e
2
2
.
(6.72)
Let us return to equation (6.58). Note that the following three types of transfor-
mations, which are particular cases of (6.65), do not change the form of the solution
under consideration affecting only the coefficients of the expansion (6.71):
(i) translations in x and in y;
(ii) rotations in the (x, y)-plane; and
(iii) the inversion
¯x =
1
r
2
x, ¯y =
1
r
2
y, ¯u =
1
r
4
u. (6.73)
The full subspace W
9
contains the invariant subspace W
4
= L{1, x
2
, y
2
, r
2
} on
which the DS (6.72) is simplified (we set a = b = 0andalsod
1
= d
2
= a
2
=
e
1
= e
2
= 0), so the general solution
u(x , y, t) = C(t) + a
1
(t)x
2
+ a
3
(t)y
2
+ G(t)r
4
will contain four arbitrary constants. Applying to this solution the abovetransforma-
tions in the (x, y)-plane, inversion and translations in ¯x and ¯y,wefind, at most, a
nine-parametric family of solutions (6.71) on the subspace W
9
.
Remark 6.39 Equation (6.70)with non-zero parametersa or b is not invariantunder
the inversion (6.73) and is mapped into
¯u
t
= F
rem
[¯u] +a ¯r
4
+ b ¯u,
where the “inhomogeneous” term a ¯r
4
belongs to the subspace (6.68), with the new
variables {¯x, ¯y}.
Example 6.40 (Quasilinear wave equation) Consider the corresponding quasilin-
ear wave equation
u
tt
= F
rem
[u] + a + bu. (6.74)
Looking for solutions (6.71) on W
9
, we obtain the DS (6.72) with the second-order
derivatives
d
2
dt
2
on the left-hand side. Similarly, (6.73) maps this equation into that
with the right-hand side in W
9
,
¯u
tt
= F
rem
[¯u] +a ¯r
4
+ b ¯u.
Example 6.41 (Pseudo-hyperbolic PDEs) The following equation which is for-
mally pseudo-hyperbolicin {u > 0}:
(I − )u
tt
≡ u
tt
− u
tt
= uu −|∇u|
2
(6.75)
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
297
is a dispersion model that describes the propagation of long 2D waves [337]. Being
restricted to (6.68), this PDE reduces to an 18D DS. A similar reduction exists for
higher-order pseudo-hyperbolicPDEs, such as
(I − )u
tt
=−α
2
u + uu −|∇u|
2
+ βu + γ u + δ. (6.76)
6.3.2 The GSV and other invariant subspaces
The remarkable operator (6.57) makes it possible to clarify interesting relations be-
tween the extended polynomial subspace and others. In general, determining invari-
ant subspaces is equivalent to a hard problem of the generalized separation of vari-
ables (GSV), which in the present remarkable case admits a special treatment. We
consider the parabolic equation (6.70). The same analysis applies to the hyperbolic
PDE (6.74).
Let us apply transformation (6.65) to the equation (6.58) to obtain another equa-
tion
¯u
t
= F
rem
[¯u] +a
(η
x
)
2
+ (η
y
)
2
+ b ¯u. (6.77)
We then impose the condition
(η
x
)
2
+ (η
y
)
2
∈
¯
W
9
= L
1, ¯x, ¯y, ¯x
2
, ¯x ¯y, ¯y
2
, ¯x ¯r
2
, ¯y ¯r
2
, ¯r
4
¯r
2
=¯x
2
+¯y
2
.
Therefore, for η(x, y), we obtain the following multi-parameter first-order PDE (a
nonlinear eigenvalue problem): to find parameters {p
1
, ..., p
9
} and η ≡ 0suchthat
(η
x
)
2
+ (η
y
)
2
= p
1
+ p
2
¯x + p
3
¯y + p
4
¯x
2
+ p
5
¯x ¯y + p
6
¯y
2
+ p
7
¯x ¯r
2
+ p
8
¯y ¯r
2
+ p
9
¯r
4
.
(6.78)
Then (6.77) will have solutions on W
9
. For instance, take
η(x, y) = e
x
cos y =¯x, so that δ(x, y) =−e
x
sin y =¯y (6.79)
by (6.64). Then (η
x
)
2
+ (η
y
)
2
= e
2x
=¯x
2
+¯y
2
=¯r
2
and ¯u = e
2x
u. The solutions
of (6.77) on
¯
W
9
are
¯u = C
1
+ C
2
¯x +C
3
¯y + C
4
¯x
2
+ C
5
¯x ¯y + C
6
¯y
2
+ C
7
¯x ¯r
2
+ C
8
¯y ¯r
2
+ C
9
¯r
4
.
In the original variables, this gives
e
2x
u = C
1
+ C
2
e
x
cos y − C
3
e
x
sin y
+C
4
e
2x
cos
2
y − C
5
e
2x
cos y sin y + C
6
e
2x
sin
2
y
+C
7
e
3x
cos y − C
8
e
3x
sin y + C
9
e
4x
.
Combining similar terms, we finally obtain
u =
1
2
(C
4
+ C
6
) + C
1
e
−2x
+ C
9
e
2x
+ (C
2
e
−x
+ C
7
e
x
) cos y
−(C
3
e
−x
+ C
8
e
x
) sin y +
1
2
(C
4
− C
6
) cos2y +
1
2
C
5
sin2y,
or, which is the same, passing to the hyperbolic functions and renaming the expan-
sion coefficients,
u =
˜
C
1
+
˜
C
2
cosh2x +
˜
C
3
sinh2x +
˜
C
8
cos2y +
˜
C
9
sin2y
+(
˜
C
4
coshx +
˜
C
5
sinh x) cos y + (
˜
C
6
coshx +
˜
C
7
sinh x) sin y.
© 2007 by Taylor & Francis Group, LLC

298 Exact Solutions and Invariant Subspaces
Therefore,the polynomialsubspaceis transformedinto the newexponential-trigonometric
invariant subspace.
Proposition 6.42
Operator
(6.57)
preserves the following subspaces:
W
4
= L{1, cosh2x, cos2y, coshx cos y}
and
(6.80)
W
9
= L
1, cosh2x, sinh2x, cos2y, sin2y,
coshx cos y, sinh x cos y, coshx sin y, sin x sin y
.
(6.81)
Of course, (6.80) is a subspace of (6.81)to functionsthat are even in both x and y.
Note that F
rem
maps even functions into even, so that the subspace of even function
from W
9
is also invariant. The above calculus of invariant transformations illustrate
how the lower-dimensional invariant subspace W
4
can be extended to W
9
.
Are there other interesting solutions of the nonlinear eigenvalue problem (6.78)
rather than (6.79)? This is an
OPEN PROBLEM.
Example 6.43 (Fast diffusion equation) The equation(6.70)admitsexactsolutions
on the subspace (6.80),
u(x , t) = C
1
+ C
2
cosh2x + C
3
cos2y + C
4
coshx cos y, (6.82)
C
1
= 4
C
2
2
− C
2
3
+ a + bC
1
,
C
2
= 4
C
1
C
2
−
1
8
C
2
4
+ bC
2
,
C
3
= 4
1
8
C
2
4
− C
1
C
3
+ bC
3
,
C
4
= 4C
4
(C
2
− C
3
) + bC
4
.
(6.83)
For a < 0, (6.69) admits positive blowing up patterns, so that solutions (6.82), (6.83)
can be used for detecting a fine structure of blow-up singularities for the case of this
critical fast diffusion operator.
Example 6.44 The fourth-orderpseudo-hyperbolicequation (6.76) can be restricted
to subspaces (6.80), or (6.81).
6.3.3 An application to systems
As in Section 5.4, the above results can be used for generating various systems of
PDEs reduced to DSs on invariant subspaces.
Example 6.45 Let us first present a formal, but exceptional application of the oper-
ator (6.57) in the following hyperbolic system in IR
2
× IR :
U
tt
=−A
2
U + BU + CF[U] + DU + E, (6.84)
where U = (u
1
, ..., u
m
)
T
, A > 0, B, C, D are m × m matrices, E ∈ IR
m
,and
F[U] = (F
rem
(u
1
), ..., F
rem
(u
m
))
T
.
The right-hand side in (6.84) preserves subspace (6.81), provided that E ∈ W
9
,so
system (6.84) restricted to W
9
is an 18mth-order DS.
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
299
Example 6.46 (Parabolic system) The parabolic system for m = 2 with remark-
able operators,
u
t
= a
1
F
rem
[u] + b
1
u + c
1
v + d
1
u + e
1
v + f
1
,
v
t
= a
2
F
rem
[v] + b
2
u + c
2
v + d
2
u + e
2
v + f
2
,
where f
1,2
∈ W
9
, being restricted to W
9
, is an 18th-order DS. Setting u =
1
U
and
v =
1
V
for positive solutions recovers a system with remarkable elliptic operators
given in (6.59), admitting an infinite-dimensional Lie group of symmetries,
U
t
= a
1
lnU +b
1
U − 2b
1
|∇U |
2
U
− c
1
U
2
1
V
− d
1
U −e
1
U
2
V
− f
1
U
2
,
V
t
= a
2
ln V − b
2
V
2
1
U
+ c
2
V − 2c
2
|∇V |
2
V
− d
2
V
2
U
− e
2
V − f
2
V
2
.
6.3.4 On partial invariant modules
Let us briefly describe invariant modules related to F
rem
that, in the 1D case, were
studied in Examples 1.37 and 1.43. Consider the PDE operator
ˆ
F[u] = u
t
− (uu −|∇u|
2
) in IR
2
× IR
+
,
and solutions of the form
u(x , t) = C
1
(t) + C
2
(t)x + C
3
(t)e
γ(t )x
e
y
, (6.85)
where γ(t) is a function. For a constant γ , the module with given basic functions
is not invariant under F
rem
, though it is composed of the invariant modules of lin-
ear functions L{1, x, y} and the exponential function W
2
= L{1, e
γ x
e
y
}.Forany
function (6.85), the following holds:
ˆ
F[u] = C
1
+ C
2
2
+ C
2
x +
C
3
− (γ
2
+ 1)C
1
C
3
+ 2γ C
2
C
3
e
γ x
e
y
+
γ
− (γ
2
+ 1)C
2
C
3
xe
γ x
e
y
,
so that we need the condition
γ
= (γ
2
+ 1)C
2
,
which deletes the last term and keeps the subspace invariant (see more details in
Example 1.37).
Example 6.47 (Parabolic equation) The fourth-order semilinear parabolic PDE
u
t
=−
2
u + (u + α)u −|∇u|
2
+ µu + ν
admits solutions (6.85) with the DS
C
1
=−C
2
2
+ µC
1
+ ν,
C
2
= µC
2
,
C
3
= (γ
2
+ 1)C
1
C
3
− 2γ C
2
C
3
+
−(γ
2
+ 1)
2
+ α(γ
2
+ 1) + µ
C
3
,
γ
= (γ
2
+ 1)C
2
.
If µ = 0, the second ODE yields C
2
(t) = e
µt
, and the last implies
γ(t) = tan
1
µ
e
µt
+ constant
.
© 2007 by Taylor & Francis Group, LLC

300 Exact Solutions and Invariant Subspaces
For µ = 0, it follows that C
2
= 1andγ
2
(t) = tant.
Similar more general solutions can be taken in the form of
u(x , y, t) = C
1
(t) + C
2
(t)x + C
3
(t)y + C
4
(t)e
γ
1
(t)x
e
γ
2
(t)y
(6.86)
with two unknown functions γ
1,2
(t). The invariance property is checked similarly.
Let us present final computations for a slightly modified model.
Example 6.48 (2mth-order parabolic equation) A higher-order PDE
u
t
= (−1)
m+1
m
u + (u + α)u −|∇u|
2
+ µu + ν
admits solutions (6.86), where the following DS occurs:
C
1
=−C
2
2
− C
2
3
+ µC
1
+ ν,
C
2
= µC
2
,
C
3
= µC
2
,
C
4
= (γ
2
1
+ γ
2
2
)C
1
C
4
− 2γ
1
C
2
C
4
− 2γ
2
C
3
C
4
+
(−1)
m+1
(γ
2
1
+ γ
2
2
)
m
+ α(γ
2
1
+ γ
2
2
) + µ
C
4
,
γ
1
=
γ
2
1
+ γ
2
2
C
2
,
γ
2
=
γ
2
1
+ γ
2
2
C
3
.
Solving independently the ODEs for coefficients {C
2
, C
3
,γ
1
,γ
2
} yields expressions
for γ
1,2
(t) similar to those given above.
6.4 On second-order p-Laplacian operators
Here, we describe specific subspaces that are admitted by operators in IR
N
with
gradient-dependent nonlinearities.
Example 6.49 (p-Laplacian operator)Consider the followingquasilinear parabolic
p-Laplacian equation with extra nonlinear and linear terms:
v
t
=∇·(|∇v|
σ
∇v) + av
1
σ +1
+ bv(v≥ 0), (6.87)
where σ>−1, σ = 0, is a fixed exponent. Equations with such nonlinearities
describe filtration in non-Newtonian dilatable (for σ>0) and pseudo-plastic (for
σ ∈ (−1, 0)) fluids, and also occur in solid fuel combustion theory (see details in
[444] and in the Remarks to Section 8.5).
In radial geometry, for solutions v = v(r, t) with r =|x |≥0, (6.87) becomes
v
t
=|v
r
|
σ
(σ + 1)v
rr
+
N−1
r
v
r
+ av
1
σ +1
+ bv.
By the transformation v = u
σ +1
σ
(similar to the PMEs, u is called the pressure in
filtration theory), we obtain
u
t
= F[u] + A + Bu, (6.88)
where F is the quasilinear operator
F[u] = µ|u
r
|
σ
(σ + 1)
uu
rr
+
1
σ
(u
r
)
2
+
N−1
r
uu
r
, (6.89)
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
301
with constants µ = (
σ +1
σ
)
σ
, A =
aσ
σ +1
,andB =
bσ
σ +1
. Though (6.89) is not a
quadratic or a cubic operator, it has the following invariant property.
Proposition 6.50
Operator
(6.89)
preserves the 2D subspace
W
r
2
= L{1, r
γ
},
where
γ =
σ +2
σ +1
.
Proof. Taking an arbitrary function from W
r
2
,
u(x , t) = C
1
(t) + C
2
(t)r
γ
, (6.90)
yields
F[u] = αC
1
C
2
|C
2
|
σ
+ β|C
2
|
σ +2
r
γ
∈ W
r
2
,
where α = µγ
σ +1
N and β = µγ
σ +1
N +γ +
γ
σ
.
The regularity properties of solutionsgiven by the pressure (6.90) well correspond
to the known typical smoothness of weak solutions of the p-Laplacian equations. In
particular, the H¨older continuity in r of the function r
γ
in (6.90) is optimal, at least
for N = 1, and in radial geometry for bell-shaped solutions (i.e., for those without
holes in the support). In the theory of quasilinear degenerate PDEs, this is proved by
Bernstein’s method; see DiBenedetto [148] and Kalashnikov [309].
Equation (6.88) restricted to W
r
2
is equivalent to the DS
C
1
= αC
1
C
2
|C
2
|
σ
+ BC
1
+ A,
C
2
= β|C
2
|
σ +2
+ BC
2
.
Let us integrate this system. Assuming for definiteness that C
2
≤ 0 (this corresponds
to finite-time extinction to be considered below) and setting C
2
≡−C with C ≥ 0,
we arrive at
C
1
=−αC
1
C
σ +1
+ BC
1
+ A,
C
=−βC
σ +2
+ BC.
(6.91)
The second ODE is independent and is integrated explicitly,
C
σ +1
(t) = B
β + H
0
e
−B(σ +1)t
−1
,
where H
0
is an arbitrary constant. In this case, from the first ODE in (6.91),
C
1
(t) =−
A
B(σ +1)
e
Bt
βe
B(σ +1)
+ H
0
−λ
E(t), (6.92)
where the function E is given by the integral related to Euler’s Beta function
E(t) =
z
δ
(β + H
0
z)
λ
dz, (6.93)
with z = e
−B(σ +1)t
, λ =
α
β(σ+1)
≡
N
(σ +1)(Nσ +σ +2)
,andδ =−
σ [N(σ +1)+σ +2]
(σ +1)(Nσ +σ +2)
.The
special case H
0
= 0 yields the constant function
C
2
=−C =−
B
β
1
σ +1
, with B > 0.
Then (6.92) implies
C
1
(t) =
H
1
e
B(1−
α
β
)t
− A
B
1 −
α
β
−1
,
where H
1
is a constant of integration. Another explicit elementary solution exists
© 2007 by Taylor & Francis Group, LLC
302 Exact Solutions and Invariant Subspaces
for A = B = 0. This solution on W
r
2
yields precisely the fundamental, instantaneous
point-source(orsource-type)solutionof the p-Laplacian equationu
t
= F[u], which
is similar to the ZKB solution for the PME; see [509, p. 84] and history therein.
Example 6.51 (Interface equation and finite-time extinction) Consider nonnega-
tive solutions of the p-Laplacian equation with absorption
v
t
=∇·
|∇v|
σ
∇v
− v
1
σ +1
in IR
N
× IR
+
, (6.94)
where σ>0. This PDE describes processes with the finite propagation, i.e., with
interfaces (free boundaries) similar to the PME. In addition, due to the presence
of the strong absorption term −v
p
with the exponent p = p
∗
=
1
σ +1
< 1, any
bounded solution has finite extinction time T and v(x , t) → 0ast → T
−
for any
x ∈ IR
N
. Furthermore, the critical absorptionexponent p
∗
=
1
σ +1
in (6.94) is known
to generate the following phenomena:
(i) the finite interface propagation no longer obeys the standard Darcy law (see [226,
Ch. 7]), and
(ii) the singular extinction behavior of the solution as t → T
−
becomes special and
differs from those which occur for p above and below the critical exponent p
∗
(see
details in [245, Ch. 4]).
Let us show that solutions on W
r
2
correctly describe both critical phenomena. Us-
ing (6.90) leads to the following explicit solutions:
v(x , t) ≡ u
σ +1
σ
(x , t) =
C
1
(t) − C(t)|x|
γ
σ +1
σ
+
, (6.95)
where the coefficients are given by
C
1
(t) =
σ
(σ +1)(1+λ)
(T
1+λ
− t
1+λ
) and C(t) = [β(σ + 1)t]
−
λ
σ +1
. (6.96)
Here, T > 0isthefinite extinction time and λ is as in (6.93).
Interface equation. It follows from (6.95) that
r = s(t) =
C
1
(t)
C(t )
σ +1
σ +2
is the interfaces of the solution. Let us derive the corresponding dynamic interface
equation. As usual, differentiating the identity for the pressure u(s(t), t) ≡ 0 implies
u
r
(s, t)s
+ u
t
= 0, which yields
s
(t) =−
1
u
r
(s(t),t )
u
t
(s(t), t), (6.97)
provided that both derivatives involved exist and the limit as r → s
−
(t) makes
sense. For the explicit solution (6.95), formula (6.97) is obviously valid. In order
to simplify the right-hand side, we calculate u
t
from the pressure equation (6.88),
(6.89) with A =−
σ
σ +1
, B = 0, so passing to the limit as r → s
−
yields
u
t
=
σ +1
σ
σ +1
|u
r
|
σ +2
−
σ
σ +1
at r = s(t).
Substituting into (6.97) determines the following dynamic interface equation:
s
(t) = S[u] ≡−
σ +1
σ
σ +1
|u
r
|
σ +1
+
σ
σ +1
1
u
r
at r = s(t), (6.98)
© 2007 by Taylor & Francis Group, LLC
