Galaktionov V.A., Svirshchevskii S.R. Exact Solutions and Invariant Subspaces of Nonlinear Partial Differential Equations in Mechanics and Physics
Подождите немного. Документ загружается.


6 Applications to Nonlinear PDEs in IR
N
303
consisting of two terms. The standard Darcy law for the pure p-Laplacian equation
contains the first term only, so, in this case, the strong absorption essentially changes
the local interface propagation. Using the whole family of exact solutions on W
r
2
makes it possible to extend (6.98) to general radial monotone solutions of (6.94) by
using the geometric Sturmian argument of intersection comparison, [226, Ch. 7].
Extinction behavior. This is also easily detected from the explicit solution (6.95).
Calculating the asymptotics of C
1
(t) in (6.96) yields, as t → T
−
,
v(x , t) =
σ
σ +1
(T − t)
1 −
|ξ|
γ
a
γ
0
σ +1
σ
+
+ ... , ξ = x/(T − t)
σ +1
σ +2
, (6.99)
where a
0
> 0 is a constant and ξ is the rescaled spatial variable. It is important that
the extinction behavior(6.99) is not self-similar,since thesimilarity rescaled variable
for (6.94) is different, η = x /(T − t). By the Sturmian intersection comparison, the
asymptotic extinction behavior (6.99) holds true for general solutions, [245, Ch. 4].
Example 6.52 (Regional blow-up) We next consider a combustion problem and
describe a blow-up behavior for the p-Laplacian equation with source
u
t
=∇·(|∇u|∇u) + u
2
in IR
N
× IR
+
. (6.100)
The operator on the right-hand side is quadratic and we use Proposition 6.9 to derive
exact solutions on a 2D subspace,
u(x , t) =
T
(T −t )t
−
T −t
T
+ f (x )
∈ L{1, f (x)}, (6.101)
where T > 0 is the blow-up time and f is a solution of the following quasilinear
elliptic PDE (the same as in Example 5.6):
∇·(|∇ f |∇ f ) + f
2
− f = 0inIR
N
(6.102)
that admits weak compactly supported solutions. For N = 1, there exists a nonneg-
ative profile f (x ) given by the incomplete Euler Beta function such that [216]
f (x)>0 on the interval
|x| <
1
2
L
S
= 2
1
3
3
−
1
2
π
.
Existence of a radial weak solution f ≥ 0 in any dimension N > 1 was proved
in [229] (the proof, in the case of regional blow-up, is the same as for the porous
medium operator in [509, p. 183]; the structure of single point blow-up similarity
patterns is completely different).It is reasonable to expect that any nonnegativecom-
pactly supported weak solution of (6.102) is radially symmetric relative to a point in
IR
N
. Such a result should involve the moving plane method via Aleksandrov’s Re-
flection Principle; see [245, p. 51].
Given a suitable nonnegative solution (6.101), we have the phenomenon of local-
ization of blow-up (regional blow-up), where, as t → T
−
,
u(x , t) →+∞ for any x inside supp f ,
and u(x, t) →−
1
T
for all x ∈ IR
N
\ supp f , as shown in Figure 6.2.
It is curious that the solution (6.101) exhibits an extremely singular behavior at
the initial moment of time t = 0. Passing to the limit t → 0
+
yields the following
© 2007 by Taylor & Francis Group, LLC
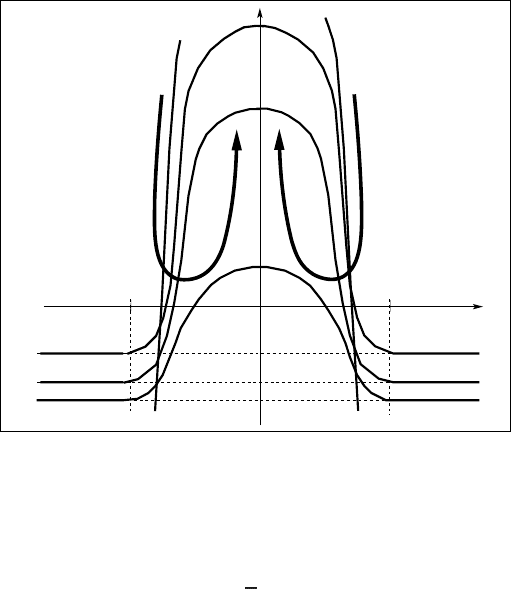
304 Exact Solutions and Invariant Subspaces
u(x , t)
t
2
t
3
0 < t
1
< t
2
< t
3
< t
4
< T
t
1
t
4
0
x
L
S
−L
S
Figure 6.2 Regional blow-up of solutions (6.101) on the interval [−L
S
, L
S
].
initial function for such solutions:
u(x , 0
+
) =
−∞, if f (x )<1,
+∞, if f (x )>1,
1
T
, if f (x) = 1.
These initial data are unbounded almost everywhere in IR
N
, but generate a bounded
weak solution that exists in IR
N
×(0, T ). Such a phenomenon is portrayedin Figure
6.2 (see the steep profile for t = t
1
≈ 0). This is an exceptional situation. Obviously,
such a local solvability of (6.100) for initial data u
0
∈ L
∞
loc
() for any arbitrarily
small domain ⊂ IR
N
is not a generic property of this PDE.
Using functions f (x) from Example 5.7, similar blow-up patterns can be con-
structed for higher-order reaction-diffusion PDEs, such as
u
t
=−(|u
xx
|u
xx
)
xx
+ u
2
and u
t
=−(|u
xxx
|u
xxx
)
x
+ u
2
.
6.5 Invariant subspaces for operators of Monge–Amp
`
ere type
6.5.1 Second-order equations
For a given function u ∈ C
2
(IR
N
),letD
2
u be the corresponding N × N Hessian
matrix #u
x
i
x
j
#. Parabolic Monge–Amp
`
ere (M-A) equations
u
t
= g
detD
2
u
+ h(x, u, D
x
u) in IR
N
× IR
+
(6.103)
play an important role in various geometric problems and applications, such as log-
arithmic Gauss and Hessian curvature flows, the Minkowski problem (1897), the
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
305
Weyl problem, the Calabi conjecture in complex geometry, and many others. See
references and basic mathematical results in [550, Ch. 14,15], [253, Ch. 17], and
[272]. For increasing functions g(s), equation (6.103) is parabolic if D
2
u(·, t) re-
mains positively definite for t > 0, assuming that D
2
u
0
> 0 for initial data u
0
.For
a class of lower-order operators h(·) satisfying necessary growth estimates, typical
monotone increasing, concave nonlinearities g in the principal operator are
g(s) = lns, g(s) =−
1
s
, and g(s) = s
1
N
for s > 0,
for which the global-in-time solvability is known. For other g(s) functions with a
faster growth as s →∞, local-in-time solutions existing by standard parabolic the-
ory (see e.g., the classic book [365, p. 320]) may blow-up in finite time. This gives
special asymptotic patterns, which sometimes are also of interest for geometric ap-
plications.
We will verifya few types of singularityformation phenomenaoccurringon linear
subspaces admitted by such Monge–Amp`ere operators. We discuss our basic exam-
ples in the 2D case N = 2 with independent variables {x, y},so
F
2
[u] = detD
2
u ≡ u
xx
u
yy
− (u
xy
)
2
. (6.104)
Example 6.53 (Motion with constant speed) In the subspace of convex parabolic
surfaces
u(x , y, t) = C
1
(t) + C
2
(t)x
2
+ C
3
(t)y
2
∈ W
3
= L{1, x
2
, y
2
}, (6.105)
with C
2
> 0, C
3
> 0, the parabolic flow with an arbitrary g,
u
t
= g(F
2
[u]),
is globally well-defined by the DS
C
1
= g(4C
2
C
3
),
C
2
= 0, C
3
= 0.
So C
2,3
(t) ≡ C
2,3
(0), from which we obtain the solution
u(x , y, t) = C
1
(0) + g(4C
2
(0)C
3
(0))t + C
2
(0)x
2
+ C
3
(0)y
2
corresponding to the motion of the surface with constant speed. For the hyperbolic
M-A equation
u
tt
= g(F
2
[u]),
the DS is of sixth order (it is of eighth order if L{xy} is included into the subspace)
C
1
= g(4C
2
C
3
),
C
2
= 0, C
3
= 0.
Initial data u
t
(x , 0) are important to keep u(x, y, t) convex and the equation hyper-
bolic. Otherwise, if D
2
u(·, t) loses its positivity, the PDE becomes of elliptic type
and possibly loses evolution setting as the Cauchy problem.
Example 6.54 (Blow-up via PME-term) Adding a standard quasilinear quadratic
© 2007 by Taylor & Francis Group, LLC

306 Exact Solutions and Invariant Subspaces
operator from PME theory to the right-hand side,
u
t
= g
detD
2
u
+ uu, (6.106)
for the same polynomial solutions (6.105), we obtain the DS
C
1
= g(4C
2
C
3
) + 2C
1
(C
2
+ C
3
),
C
2
= 2C
2
(C
2
+ C
3
),
C
3
= 2C
3
(C
2
+ C
3
).
From the last two ODEs, it follows that C
3
= AC
2
, with a constant A > 0, so
C
2
= 2(1 + A)C
2
2
, which yields finite-time blow-up of C
1,2,3
(t) with the rate
C
2
(t) =
1
2(1+A)
1
T −t
.
This blow-up is induced by the quadratic operator on the right-hand side of (6.106),
so, in this sense, the M-A operator is weaker on such polynomial profiles.
Example 6.55 (Blow-up in quadratic equations) We next consider the parabolic
equation with g(s) = s,
u
t
= F
2
[u] ≡ u
xx
u
yy
− (u
xy
)
2
. (6.107)
The basic subspace for F
2
consists of arbitrary fourth-degree polynomials,
W
15
= L{x
α
y
β
, 0 ≤ α + β ≤ 4}. (6.108)
For simplicity, consider solutions on a smaller subspace W
6
,
u(x , y, t) = C
1
+ C
2
x
2
+ C
3
y
2
+ C
4
x
2
y
2
+ C
5
x
4
+ C
6
y
4
, (6.109)
C
1
= 4C
2
C
3
,
C
2
= 24C
3
C
5
+ 4C
2
C
4
,
C
3
= 4C
3
C
4
+ 24C
2
C
6
,
C
4
=−12C
2
4
+ 144C
5
C
6
,
C
5
= 24C
4
C
5
,
C
6
= 24C
4
C
6
.
(6.110)
The last two ODEs yield C
6
= AC
5
, with A > 0. Then we obtain two independent
equations for {C
4
, C
5
},
C
4
=−12C
2
4
+ 144AC
2
5
,
C
5
= 24C
4
C
5
,
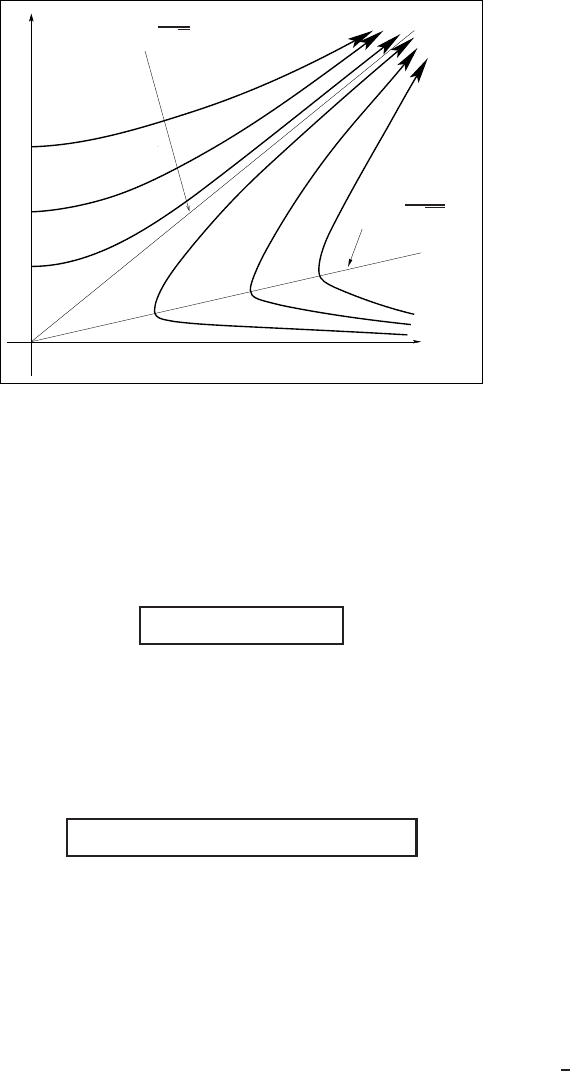
which are integrated in quadratures. The phase-plane of the first-order ODE
dC
5
dC
4
=
2C
4
C
5
12AC
2
5
−C
2
4
(6.111)
is given in Figure 6.2, which shows that all positive orbits blow-up in finite time and
approach the explicit solution C
5
=
1
2
√
A
C
4
, corresponding to coefficients
C
4
(t) =
1
24
1
T −t
,
C
5
(t) =
1
48
√
A
1
T −t
,
C
6
(t) =
√
A
48
1
T −t
.
(6.112)
© 2007 by Taylor & Francis Group, LLC
6 Applications to Nonlinear PDEs in IR
N
307
C
4
C
5
C
5
=
1
2
√
A
C
4
C
5
=
1
2
√
3A
C
4
0
Figure 6.3 The phase-plane of (6.111): stability of the explicit solution (6.112).
The rest of the coefficients can also be calculated explicitly from the first three ODEs
(6.110), and these are also singular as t → T
−
. In the class of fourth-degreepolyno-
mials (6.109), the solution of the parabolic M-A equation (6.107) is essentially local
in time, u(x , y, t) →∞as t → T
−
. This blow-up is connected with the exceeding
growth of convex initial data at infinity.
The blow-up phenomenon can also be detected for the hyperbolic equation
u
tt
= u
xx
u
yy
− (u
xy
)
2
,
where the DS with the right-hand sides from (6.110) is of twelfth order and, as is
usual for such quadratic systems, the blow-up rate is now ∼ (T −t)
−2
. For the whole
subspace(6.108), the DS is of thirties order and cannotbe reduced for arbitraryinitial
data, unlike the parabolic case.
Example 6.56 (Higher-order regularization) Consider a fourth-order parabolic
regularization of the above M-A equation,
u
t
= u
xx
u
yy
− (u
xy
)
2
− u
2
u (u > 0).
Then the last three ODEs of the DS (6.110) take the form
C
4
=−20C
2
4
+ 144C
5
C
6
− 24C
4
(C
5
+ C
6
),
C
5
= 8(2C
4
− 3C
5
− 3C
6
)C
5
,
C
6
= 8(2C
4
− 3C
5
− 3C
6
)C
6
.
Again C
6
= AC
5
from the last two ODEs, so the blow-up behavior (or a global one
due to the fourth-order regularization) can be studied on the {C
4
, C
5
}-plane.
Example 6.57 (Extinction for a parabolic equation) We next consider the extinc-
tion phenomenon for the M-A equation associated with the nonlinearity g(s) =−
1
s
,
© 2007 by Taylor & Francis Group, LLC

308 Exact Solutions and Invariant Subspaces
where an extra linear multiplier u is included,
u
t
=−
u
detD
2
u
. (6.113)
For solutions (6.105), the DS takes the form
C
1
=−
C
1
4C
2
C
3
,
C
2
=−
1
4C
3
,
C
3
=−
1
4C
2
.
Integrating yields the following solutions:
u(x , y, t) =
√
T − t
B +
1
2A
x
2
+
A
2
y
2
, (6.114)
where A and B are arbitrary positive constants. These separate variables solutions
vanish as t → T
−
, and represent a singular extinction pattern. Let us describe the
corresponding asymptotic problem for more general solutions having extinction at
the same moment t = T . Introducing the rescaled function according to (6.114),
u(x , t) =
√
T − t v(x, y,τ), τ =−ln(T − t) →+∞, (6.115)
yields the rescaled PDE
v
τ
=−
v
detD
2
v
+
1
2
v. (6.116)
Typical second-order Hessian operators are known to be potential and the corre-
sponding smooth parabolic flows are gradient systems. For M-A PDEs, these ideas
go back to Bernstein (1910) [51]; see also Reilly [486], and [462] for a particular
case. For (6.116), the Lyapunov functional is given by
(v) =−
1
3
v detD
2
v + 2
v.
Here, we assume integrationovera boundeddomain ⊂ IR
2
withsuitable boundary
conditions on ∂, so the manipulations make sense. For the problem in IR
N
,extra
conditions at infinity are necessary, as well as suitable changing of the functional.
Using (6.116) then yields
d
dτ
(v) =−
v
τ
detD
2
v − 2
≡−
v(detD
2
v−2)
2
2detD
2
v
≤ 0. (6.117)
On the other hand, this is equivalent to an L
2
-bound of the time-derivative v
τ
,
∞
dτ
2detD
2
v
v
(v
τ
)
2
< ∞, (6.118)
which shows that the ω-limit set of the rescaled orbit satisfying (6.116) consists of
stationary points only. A rigorous application of gradient systems theory for (6.116)
also demands some delicate estimates of the rescaled orbits; e.g., to provethat v(·,τ)
is uniformlyboundedandboundedfrom belowforτ 1.This is not easyfor scaling
(6.115), which is singular as t → T
−
(τ →+∞). These problems are OPEN.
Example 6.58 (Extinction for a hyperbolic equation) The corresponding hyper-
bolic M-A equation
u
tt
=−
u
detD
2
u
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
309
admits solutions
u(x , y, t) = C
1
(t)
1 + Ax
2
+ By
2
,
where A, B > 0 are constants and C
1
satisfies the ODE C
1
=−
1
4AB
1
C
1
. It admits
solutions vanishing in finite time with the generic behavior
C
1
(t) = (T − t) −
1
4AB
(T − t) ln(T − t) + ... as t → T
−
.
This represents an asymptotic separate variables extinction pattern that describes a
stable extinction behavior on W
3
. A stability theory is absent and OPEN.
Example 6.59 (Blow-up) For the parabolic M-A equation
u
t
= u
√
detD
2
u in IR
2
× IR
+
, (6.119)
the solutions (6.105) lead to the DS
C
1
= 2C
1
√
C
2
C
3
,
C
2
= 2C
2
√
C
2
C
3
,
C
3
= 2C
3
√
C
2
C
3
.
This gives blow-up solutions in separate variables,
u(x , y, t) =
1
2
√
AB
1
T −t
1 + Ax
2
+ By
2
→∞ as t → T
−
,
where A, B > 0. For the corresponding hyperbolic M-A equation
u
tt
= u
√
detD
2
u in IR
2
× IR
+
,
there are the following blow-up solutions in separate variables:
u(x , y, t) = C
1
(t)
1 + Ax
2
+ By
2
, with C
1
= 2
√
AB C
2
1
.
TheDSforthecoefficients {C
1
, C
2
, C
3
} shows that this pattern is stable on W
3
(the
analysis is similar to that for hyperbolic equations in Example 5.1). The generic
blow-up behavior on the subspace W
3
(in general, stability is OPEN)isgivenby
C
1
(t) ∼
3
√
AB
1
(T −t )
2
as t → T
−
.
Example 6.60 The logarithmic Gauss curvature flow in terms of the support func-
tion (see [122]) is described by the M-A-type equation
u
t
=
1 +|x|
2
ln
detD
2
u
+ h in IR
N
× IR
+
,
where h is given.Depending on the initial uniformly convexhypersurfaces,this PDE
is known to admit either a local solution, corresponding to shrinking to a point in fi-
nite time or a global solution that describes the uniform convergenceto an expanding
sphere.
Consider a simpler related version of this M-A-type equation
u
t
= (1 +|x|
2
)g
detD
2
u
in IR
N
× IR
+
and pose the same question of the blow-up or global existence of solutions. Taking
© 2007 by Taylor & Francis Group, LLC
310 Exact Solutions and Invariant Subspaces
solutions on the subspace of second-degree polynomials,
u(x , t) = C
0
(t) + C
1
(t)x
2
1
+ ... + C
N
(t)x
2
N
,
their dynamics are governed by the DS
C
k
= g
2
N
C
1
...C
N
for k = 0, 1, ..., N .
It follows that blow-up solutions appear iff Osgood’s criterion holds
∞
ds
&
g(s
N
)<∞.
If the integral diverges, the flow is globally defined in t. For the hyperbolic PDE
u
tt
= (1 +|x|
2
)g
detD
2
u
in IR
N
× IR
+
,
taking the solutions in separate variables
u(x , t) = C
1
(t)
1 + A
1
x
2
1
+ ... + A
N
x
2
N
yields the ODE
C
1
= g
2
N
A
1
...A
N
C
N
1
,
so blow-up occurs via another Osgood criterion
∞
ds
&
g(s
N
)ds < ∞.
Example 6.61 Finally, consider the following PDE (see Remarks for a motivation
for such models):
u
t
= F
2
[u] ≡ detD
2
u − u
2
in IR
2
× IR
+
. (6.120)
In order to describe main aspects of blow-up for such M-A equations, we present an
invariant analysis of (6.120) in radial geometry with the spatial variable r =|x |,so
u
t
= F
2
[u] ≡
1
r
u
r
u
rr
− u
2
in IR
+
× IR
+
. (6.121)
The origin,r = 0, is a regular point of the operator on the right-hand side. Indeed, by
L’Hospital’s rule, for strictly convex C
2
-solutions,
1
r
u
r
u
rr
→ (u
rr
)
2
> 0asr → 0.
Consider solutions satisfying
u < 0, u
r
> 0, and u
rr
> 0, (6.122)
on which the equation is uniformly parabolic. Let us construct exact solutions
u(r, t) = C
1
(t) + C
2
(t) f (r ) ∈ L{1, f }, (6.123)
with some unknown function f . Plugging (6.123) into (6.121), and assuming that f
solves the ODE problem
1
r
f
f
= f
2
, f < 0forr ∈ (0, r
0
), f
(0) = 0, f (r
0
) = 0, (6.124)
(where L{1, f } is invariant under F
2
) yields the DS
C
1
=−C
2
1
,
C
2
=−2C
1
C
2
.
© 2007 by Taylor & Francis Group, LLC

6 Applications to Nonlinear PDEs in IR
N
311
This gives blow-up solutions
u(r, t) =−
1
T −t
+
A
(T −t)
2
f (r), with A > 0. (6.125)
These solutions have singularity at the degeneracy point r = r
0
,whereu
rr
= 0by
(6.124), so solutions are not strictly convex. The PDE is degenerate and loses its uni-
form parabolicity.It followsthat,for solutions(6.123) defined for all r > 0, the point
r = r
0
is the only point of degeneracy (u
rr
> 0forallr = r
0
). Nevertheless, the
strong Maximum Principle for u
rr
does not apply, and this singularity point persists
until the blow-up time t = T . Introducing the rescaled function
u(r, t) =
1
(T −t)
2
v(r,τ), where τ =
1
T −t
,
gives the rescaled equation with an O(
1
τ
)-perturbation,
v
τ
=
1
r
v
r
v
rr
− v
2
−
2
τ
v. (6.126)
Notice that, for solutions v(r,τ) of (6.126), the “waiting time” of the singularity at
r = r
0
is infinite. Exact solutions (6.125) show the convergence as τ →∞,
v(r,τ)≡−
1
τ
+ Af(r) → Af(r).
The passage to the limit in the general equation (6.126) is an
OPEN PROBLEM.
In addition, (6.121) admits separate variablessolutionswitha weaker blow-uprate
¯u(r, t) =
1
T −t
¯
f (r),
where
¯
f solves the ODE
1
r
¯
f
¯
f
=
¯
f
2
+
¯
f for r ∈ (0, r
0
),
¯
f
(0) = 0,
¯
f (r
0
) = 0;
u(r, t) = C
1
(t) + C
2
(t)
¯
f (r),
C
1
=−C
2
1
,
C
2
=−2C
1
C
2
+ C
2
2
.
The regularity convexity assumption,
¯
f
> 0, determines another singularity point
r =¯r
0
> 0suchthat
¯
f (¯r
0
) =−1 with different boundary conditions that give such
a blow-up solution. The rescaled solution now takes the form
u(r, t) =
1
T −t
w(r, s), where s =−ln(T − t),
and satisfies the autonomous, unperturbed PDE with a potential operator
w
s
=
1
r
w
r
w
rr
− w
2
− w.
A Lyapunov function is obtained by multiplying by rw
s
in L
2
with suitable bound-
ary conditions. The passage to the limit as s →∞demonstrates that, for general
solutions, w(r, s) →¯g(r).
For the M-A equation with absorption
u
t
=
1
r
u
r
u
rr
+ u
2
(u < 0)
© 2007 by Taylor & Francis Group, LLC
cf. (6.124). The corresponding exact solutions are

312 Exact Solutions and Invariant Subspaces
in the class (6.122), the generic decay behavior is expected to be described by the
separable solution
u(r, t) =
1
T +t
˜
f (r), where
1
r
˜
f
˜
f
+
˜
f
2
=−
˜
f
and
˜
f (0) ∈ (−1, 0). Hence, the equation is degenerate at some point r
0
,atwhich
˜
f (r
0
) = 0. It is easy to construct solutions on the subspace L{1,
˜
f }.
The above subspaces can be used for studying singularity formation phenomena
for hyperbolicM-A models in radial geometry,
u
tt
=
1
r
u
r
u
rr
± u
2
.
6.5.2 On higher-order Monge–Amp
`
ere-type equations
We discuss some typesof higher-order M-A equationsadmitting invariantsubspaces.
Existence,uniqueness, and regularity theory of such PDEs is not well developed,ex-
cluding a few particular cases; see Remarks.
Example 6.62 (Fourth-order Hessian equations) In order to formulate fourth-
order Hessian equations in IR
2
, let us write down the fourth differential of a C
4
-
function u = u(x, y) as a quartic form
d
4
u = u
xxxx
dx
4
+ 4u
xxxy
dx
3
dy + 6u
xxyy
dx
2
dy
2
+ 4u
xyyy
dxdy
3
+ u
yyyy
dy
4
.
This gives the catalecticant determinant
F
4
[u] = detD
4
u ≡ det
'
u
xxxx
u
xxxy
u
xxyy
u
xxxy
u
xxyy
u
xyyy
u
xxyy
u
xyyy
u
yyyy
(
,
which plays an important role in the theory of quartic forms. For instance, each such
form in two variables can be expressed via a sum of three fourth powers of linear
forms and via two powers, provided that det D
4
u = 0; see [281].
We will use F
4
[u] for constructionof some geometric flows. Clearly, F
4
preserves
the subspace of fourth-degreepolynomials W
7
= L{1, x
2
, xy, y
2
, x
4
, x
2
y
2
, y
4
} and
F
4
: W
7
→ L{1}.Therefore,the flow u
t
= F
4
[u]is globalon W
7
.The basic invariant
subspace of sixth-degree polynomials is
W = L{x
α
y
β
, 0 ≤ α +β ≤ 6}, (6.127)
on which blow-up may happen via a cubic DS. Singular patterns also exist for other
fourth-order M-A-type models that are constructed in accordance to their second-
order counterparts.
Example 6.63 (Extinction and blow-up) Equation
u
t
=−
u
detD
4
u
in IR
2
× IR
+
admits solutions on W
4
,
u(x , y, t) = C
1
(t) + C
2
(t)x
4
+ C
3
(t)x
2
y
2
+ C
4
(t)y
4
.
© 2007 by Taylor & Francis Group, LLC
