Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

goes like this:

x ¼ð4  j8

1=2

Þ=ð6Þ

¼ 4=6  j½8

1=2

=ð6Þ

¼ 2=3  j½2  2

1=2

=ð6Þ

¼ 2=3  j½2=ð6Þ2

1=2



¼ 2=3  jð1=3  2

1=2

¼ 2=3 ½jð1=3  2

1=2

Þ

¼ 2=3  jð1=3  2

1=2

This might not look any ‘‘simpler’’ at ﬁrst glance, but it’s good practice to

state complex numbers in standard form, and reduced to lowest fractions.

The last step, in which the minus sign disappears, is justiﬁed because adding

a negative is the same thing as subtracting a positive, and subtracting a

negative is the same thing as adding a positive.

Fig. 6-4. The complex number plane portrays real numbers on the horizontal axis and

imaginary numbers on the vertical axis.

CHAPTER 6 More Algebra 131

The two complex solutions to the equation can be stated separately

this way:

x ¼ 2=3 þ jð1=3  2

1=2

x ¼ 2=3  jð1=3  2

1=2

PROBLEM 6-5

Solve the following equation using the quadratic formula:

þ 9 ¼ 0

SOLUTION 6-5

In standard form showing all three coeﬃcients a, b, and c, the equation

looks like this:

þ 0x þ 9 ¼ 0

Thus the coeﬃcients are:

a ¼ 1

b ¼ 0

c ¼ 9

Plugging these numbers into the quadratic formula yields:

x ¼f0 ½0

ð4  1  9Þ

1=2

g=ð2  1Þ

¼ ð36Þ

1=2

¼j6=2

¼j3

PROBLEM 6-6

Write out the quadratic equation from the preceding problem in factored

form.

SOLUTION 6-6

This would be tricky if we didn’t already know the solutions. But we do, so

it’s easy:

ðx þ j3Þðx  j3Þ¼0

You can verify that this works by ‘‘plugging in’’ the solutions derived from

the quadratic formula in the previous problem.

PART 2 Finding Unknowns

132

One-Variable, Higher-Order Equations

As the exponents in single-variable equations get bigger, ﬁnding the

solutions becomes a more challenging business. In the olden days, a lot of

insight, guesswork, and tedium was involved in solving such equations.

Today, scientists have the help of computers, and when problems are

encountered containing equations with variables raised to large powers,

they just let a computer take over. The material here is presented so you

won’t be taken aback if you ever come across one-variable, higher-order

equations.

THE CUBIC

A cubic equation, also called a one-variable, third-order equation or a

third-order equation in one variable, can be written in the following standard

form:

þ bx

þ cx þ d ¼ 0

where a, b, c, and d are constants, x is the variable, and a 6¼ 0.

If you’re lucky, you’ll be able to reduce a cubic equation to factored form

to ﬁnd real-number solutions r, s, and t:

ðx þ rÞðx þ sÞðx þ tÞ¼0

Don’t count on being able to factor a cubic equation. Sometimes it’s easy,

but most of the time it is nigh impossible. There is a cubic formula that can

be used in a manner similar to the way in which the quadratic formula is

used for quadratic equations, but it’s complicated, and is beyond the scope

of this discussion.

Plotting cubics

When we substitute y for 0 in the standard form of a cubic equation and

then graph the resulting relation with x on the horizontal axis and y on

the vertical axis, a curve with a characteristic shape results.

Figure 6-5 is a graph of the simplest possible cubic equation:

¼ y

CHAPTER 6 More Algebra 133

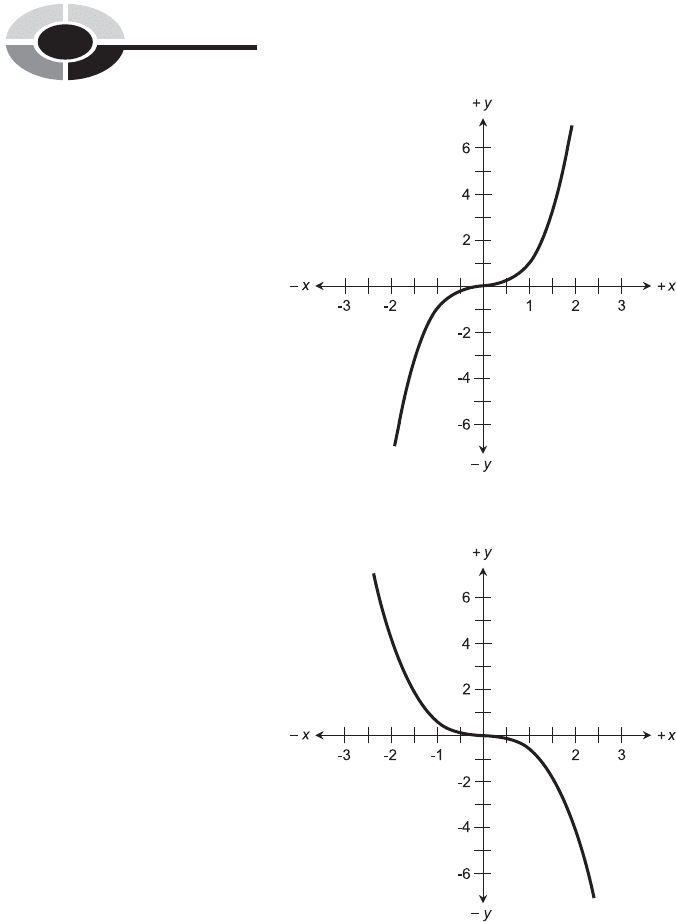
The domain and range of this function both encompass the entire set of real

numbers. This makes the cubic curve diﬀerent from the parabola, whose

range is always limited to only a portion of the set of real numbers.

Figure 6-6 is a graph of another simple cubic:

ð1=2Þx

¼ y

In this case, the domain and range also span all the real numbers.

Fig. 6-5. Graph of the cubic equation x

¼ y.

Fig. 6-6. Graph of the cubic equation (1/2)x

¼ y.

PART 2 Finding Unknowns

134

The inﬂection point, or the place where the curve goes from concave down-

ward to concave upward, is at the origin (0, 0) in both Fig. 6-5 and Fig. 6-6.

This is because the coeﬃcients b, c, and d are all equal to 0. When these

coeﬃcients are nonzero, the inﬂection point is not necessarily at the origin.

THE QUARTIC

A quartic equation, also called a one-variable, fourth-order equation or a fourth-

order equation in one variable, can be written in the following standard form:

þ bx

þ cx

þ dx þ e ¼ 0

where a, b, c, d, and e are constants, x is the variable, and a 6¼ 0.

Once in a while you will be able to reduce a quartic equation to factored

form to ﬁnd real-number solutions r, s, t, and u:

ðx þ rÞðx þ sÞðx þ tÞðx þ uÞ¼0

As is the case with the cubic, you will be lucky if you can factor a quartic

equation into this form and thus ﬁnd four real-number solutions with ease.

Plotting quartics

When we substitute y for 0 in the standard form of a quartic equation and

then graph the resulting relation with x on the horizontal axis and y on

the vertical axis, a curve with a ‘‘parabola-like’’ shape is the result. But this

curve is not a true parabola. It is distorted – ﬂattened down in a sense – as

can be seen when it is compared with a true parabola. The bends in the

curve are sharper than those in the parabola, and the curve ‘‘takes oﬀ’’

more steeply beyond the bends.

Figure 6-7 is a graph of the simplest possible quartic equation:

¼ y

The domain encompasses the whole set of real numbers, but the range of

this function spans only the non-negative real numbers. Figure 6-8 is a

graph of another simple quartic:

ð1=2Þx

¼ y

In this case, the domain spans all the real numbers, but the range spans only

the non-positive real numbers.

You are welcome to ‘‘play around’’ with various quartic equations to see

what their graphs look like. Their shapes, positions, and orientations can

vary depending on the values of the coeﬃcients b, c, d, and e.

CHAPTER 6 More Algebra 135

THE QUINTIC

A quintic equation, also called a one-variable, ﬁfth-order equation or a ﬁfth-

order equation in one variable, can be written in the following standard form:

þ bx

þ cx

þ dx

þ ex þ f ¼ 0

where a, b, c, d, e, and f are constants, x is the variable, and a 6¼ 0.

Fig. 6-7. Graph of the quartic equation x

¼ y.

Fig. 6-8. Graph of the quartic equation (1/2)x

¼ y.

PART 2 Finding Unknowns

136

There is a remote possibility that, if you come across a quintic, you’ll be

able to reduce it to factored form to ﬁnd real-number solutions r, s, t,

u, and v:

ðx þ rÞðx þ sÞðx þ tÞðx þ uÞðx þ vÞ¼0

As is the case with the cubic and the quartic, you will be lucky if you can

factor a quintic equation into this form.

Plotting quintics

When we substitute y for 0 in the standard form of a quintic equation and

then graph the resulting relation with x on the horizontal axis and y on

the vertical axis, the resulting curve looks something like that of the graph

of the cubic equation. The diﬀerence is that the bends are sharper, and the

graphs run oﬀ more steeply toward ‘‘positive inﬁnity’’ and ‘‘negative inﬁnity’’

beyond the bends.

Figure 6-9 is a graph of the simplest possible quintic equation:

¼ y

The domain and range of this function both span the set of reals. Figure 6-10

is a graph of another simple quintic:

ð1=2Þx

¼ y

In this case, the domain and range also span all the real numbers.

Fig. 6-9. Graph of the quintic equation x

¼ y.

CHAPTER 6 More Algebra 137

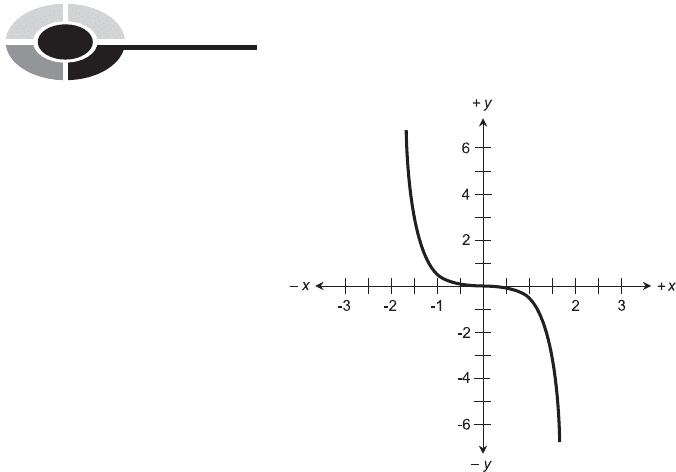
The inﬂection point for the graph of the quintic is at the origin in both

Fig. 6-9 and Fig. 6-10. As in the case of equations of lower order that are

shown in this chapter, the reason is that the coeﬃcients other than a are all

equal to 0.

THE nth-ORDER EQUATION

A one-variable, nth-order equation can be written in the following standard

form:

þ a

n1

þ a

n2

þþa

n2

þ a

n1

x þ a

¼ 0

where a

, a

, ..., a

are constants, x is the variable, and a

6¼ 0. We won’t

even think about trying to factor an equation like this in general, although

speciﬁc cases might lend themselves to factorization. Solving nth-order

equations, where n>5, practically demands the use of a computer.

PROBLEM 6-7

What happens to the general shape of the graph of the following equation if

n is a positive even integer and n becomes larger without limit?

¼ y

SOLUTION 6-7

If x ¼ 0, then y ¼ 0. If x ¼1orx ¼ 1, then y ¼ 1. These two facts are true no

matter what the value of n, as long as it is even. As n increases, the curve

Fig. 6-10. Graph of the quintic equation (1/2)x

¼ y.

PART 2 Finding Unknowns

138

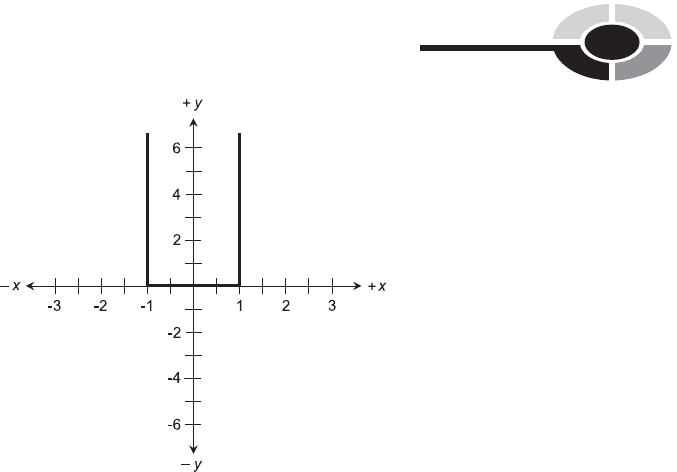
tends more and more toward 0 from the positive side when 1<x<0 and

when 0 < x < 1. Also, the curve rises ever-more-steeply toward ‘‘positive

inﬁnity’’ (þ1) when x < 1orx>1. Figure 6-11 is an approximate draw-

ing of the graph of the equation x

998

¼ y. The bends are not perfectly

squared-oﬀ, but they’re pretty close. The curve ‘‘takes oﬀ’’ in almost, but

not perfectly, vertical directions.

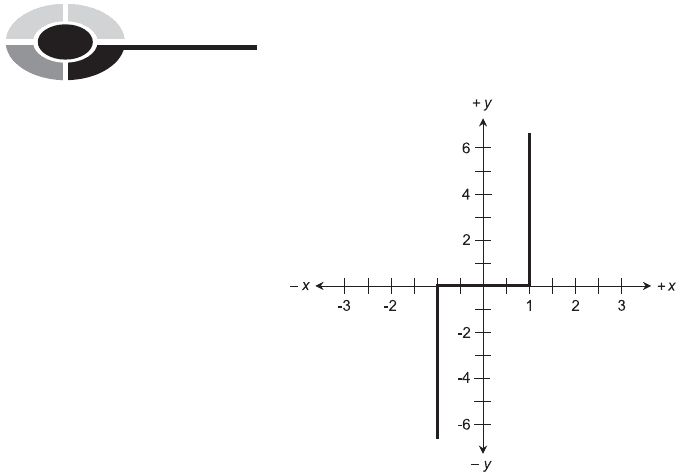
PROBLEM 6-8

What happens to the general shape of the graph of the following equation if

n is a positive odd integer and n becomes larger without limit?

¼ y

SOLUTION 6-8

If x ¼ 0, then y ¼ 0. If x ¼1, then y ¼1. If x ¼ 1, then y ¼ 1. These two

facts are true regardless of the value of n, as long as it is odd. As n increases,

the curve tends more and more toward 0 from the negative side when

1<x < 0, and more and more toward 0 from the positive side when

0<x < 1. The curve descends ever-more-steeply toward ‘‘negative inﬁnity’’

(1) when x < 1, and rises ever-more-steeply toward ‘‘positive inﬁnity’’

(þ1) when x>1. Figure 6-12 is an approximate drawing of the graph of

the equation x

999

¼ y. As with the curve shown in Fig. 6-11, the ‘‘take-oﬀ’’

slopes are almost, but not quite, vertical.

Fig. 6-11. Illustration for Problem 6-7.

CHAPTER 6 More Algebra 139

Quiz

Refer to the text in this chapter if necessary. A good score is eight correct.

Answers are in the back of the book.

1. A point on the graph of a function where the curve goes from concave

upward to concave downward is called

(a) an inﬂection point

(b) a focal point

(d) a slope point

2. The general form of a quadratic equation is:

þ bx þ c ¼ 0

Suppose a is a negative real number, b and c are real numbers, and

 4ac) ¼ 0. Then which of the following statements is true?

(a) The equation has a real-number solution.

(b) The equation has two diﬀerent real-number solutions.

(d) The equation has no solutions at all.

3. The equation x

¼ 3x

þ 2 is an example of

(a) a second-order equation

Fig. 6-12. Illustration for Problem 6-8.

PART 2 Finding Unknowns

140