Gibilisco S. Everyday Math Demystified: A Self-Teaching Guide

Подождите немного. Документ загружается.

(b) a third-order equation

(d) a ﬁfth-order equation

4. Which of the following equations has a graph that is not a parabola?

(a) x

¼ y

(b) x

þ 2x ¼ y

 2x þ 4 ¼ y

(d) 4x þ 5 ¼ y

5. In standard form, the factored equation (x  10)(x þ 10) ¼ 0 is:

(a) x

þ 10x þ 100 ¼ 0

(b) x

 10x  100 ¼ 0

þ 100 ¼ 0

(d) x

 100 ¼ 0

6. What is, or are, the real-number solutions of the equation (x  10)

(x þ 10) ¼ 0?

(a) 10

(b) 10

(d) There are none.

7. Which of the following numbers, when multiplied by itself, is equal

to 100?

(a) 10

(b) 10

(d) 10 þ j10

8. The domain of the function 2x

 x

þ 4x þ 2 ¼ y consists of

(a) the set of real numbers greater than 2

(b) the set of real numbers smaller than 2

(d) the entire set of real numbers

9. Consider the following equation:

ðx  6Þðx þ j10Þðx  14Þðx þ j2Þ¼0

Which of the following numbers is not a solution to this equation?

(a) 6

(b) 14

(d) j10

CHAPTER 6 More Algebra 141

10. The solution(s) to the equation x

 2 ¼ 0 is or are

(a) imaginary

(b) real, but irrational

(d) nonexistent

PART 2 Finding Unknowns

142

CHAPTER

A Statistics Sampler

If you want to understand anything about a scientiﬁc discipline, you must

know the terminology. Statistics is no exception. This chapter deﬁnes some

of the most common terms used in statistics.

Experiments and Variables

Statistics is the analysis of information. In particular, statistics is concerned

with data: information expressed as measurable or observable quantities.

Statistical data is usually obtained by looking at the real world or universe,

although it can also be generated by computers in ‘‘artiﬁcial worlds.’’

EXPERIMENT

In statistics, an experiment is an act of collecting data with the intent of learn-

ing or discovering something. For example, we might conduct an experiment

143

to determine the most popular channels for frequency-modulation (FM)

radio broadcast stations whose transmitters are located in American

towns having less than 5000 people. Or we might conduct an experiment

to determine the lowest barometric pressures inside the eyes of all the

Atlantic hurricanes that take place during the next 10 years.

Experiments often, but not always, require specialized instruments to

measure quantities. If we conduct an experiment to ﬁgure out the average test

scores of high-school seniors in Wyoming who take a certain standardized

test at the end of this school year, the only things we need are the time,

energy, and willingness to collect the data. But a measurement of the

minimum pressure inside the eye of a hurricane requires sophisticated

hardware in addition to time, energy, and courage.

VARIABLE (IN GENERAL)

In mathematics, a variable, also called an unknown, is a quantity whose

value is not necessarily speciﬁed, but that can be determined according to

certain rules. Mathematical variables are expressed using italicized letters

of the alphabet, usually in lowercase. For example, in the expression

x þ y þ z ¼ 5, the letters x, y, and z are variables that represent numbers.

In statistics, variables are similar to those in mathematics. But there

are some subtle distinctions. Perhaps most important is this: In statistics, a

variable is always associated with one or more experiments.

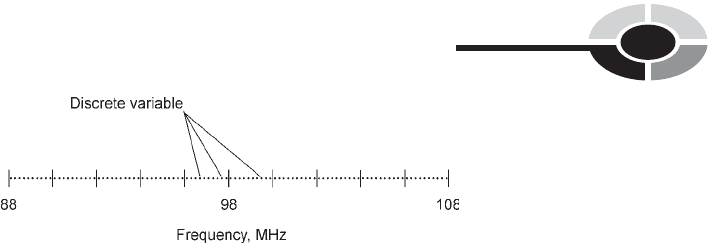
DISCRETE VARIABLE

In statistics, a discrete variable is a variable that can attain only speciﬁc

values. The number of possible values is countable. Discrete variables

are like the channels of a television set or digital broadcast receiver. It’s

easy to express the value of a discrete variable, because it can be assumed

exact.

When a disc jockey says ‘‘This is radio 97.1,’’ it means that the assigned

channel center is at a frequency of 97.1 megahertz, where a megahertz (MHz)

represents a million cycles per second. The assigned channels in the FM

broadcast band are separated by an increment (minimum diﬀerence)

of 0.2 MHz. The next lower channel from 97.1 MHz is at 96.9 MHz, and

the next higher one is at 97.3 MHz. There is no ‘‘in between.’’ No two

channels can be closer together than 0.2 MHz in the set of assigned standard

FM broadcast channels in the United States. The lowest channel is at

88.1 MHz and the highest is at 107.9 MHz (Fig. 7-1).

PART 2 Finding Unknowns

144

Other examples of discrete variables are:

The number of people voting for each of the various candidates in a

political election.

The scores of students on a standardized test (expressed as a percent-

age of correct answers).

The number of car drivers caught speeding every day in a certain town.

The earned-run averages of pitchers in a baseball league (in runs per 9

innings or 27 outs).

All these quantities can be expressed as exact values.

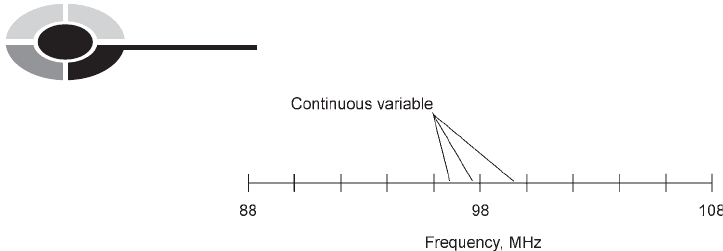
CONTINUOUS VARIABLE

A continuous variable can attain inﬁnitely many values over a certain span or

range. Instead of existing as speciﬁc values in which there is an increment

between any two, a continuous variable can change value to an arbitrarily

tiny extent.

Continuous variables are something like the set of radio frequencies to

which an analog FM broadcast receiver can be tuned. The radio frequency is

adjustable continuously, say from 88 MHz to 108 MHz for an FM headset

receiver with analog tuning (Fig. 7-2). If you move the tuning dial a little,

you can make the received radio frequency change by something less than

0.2 MHz, the separation between adjacent assigned transmitter channels.

There is no limit to how small the increment can get. If you have a light

enough touch, you can adjust the received radio frequency by 0.02 MHz, or

0.002 MHz, or even 0.000002 MHz.

Other examples of continuous variables are:

Temperature in degrees Celsius.

Barometric pressure in millibars.

Brightness of a light source in candela.

Intensity of the sound from a loudspeaker in decibels with respect to

the threshold of hearing.

Fig. 7-1. The individual channels in the FM broadcast band constitute values of a

discrete variable.

CHAPTER 7 A Statistics Sampler 145

Such quantities can never be determined exactly. There is always some instru-

ment or observation error, even if that error is so small that it does not have a

practical eﬀect on the outcome of an experiment.

Populations and Samples

In statistics, the term population refers to a particular set of items, objects,

phenomena, or people being analyzed. These items, also called elements,

can be actual subjects such as people or animals, but they can also be

numbers or deﬁnable quantities expressed in physical units.

Consistent with the above deﬁnitions of variables, some examples of

populations are as follows:

Assigned radio frequencies (in megahertz) of all FM broadcast trans-

mitters in the United States.

Temperature readings (in degrees Celsius) at hourly intervals last

Wednesday at various locations around the city of New York.

Minimum barometric-pressure levels (in millibars) at the centers of

all the hurricanes in recorded history.

Brightness levels (in candela) of all the light bulbs in oﬃces in

Minneapolis.

Sound-intensity levels (in decibels relative to the threshold of hearing)

of all the electric vacuum cleaners in the world.

SAMPLE, EVENT, AND CENSUS

A sample of a population is a subset of that population. It can be a set

consisting of only one value, reading, or measurement singled out from a

population, or it can be a subset that is identiﬁed according to certain

Fig. 7-2. The frequency to which an analog FM broadcast receiver can be set is an example

of a continuous variable.

PART 2 Finding Unknowns

146

characteristics. The physical unit (if any) that deﬁnes a sample is always the

same as the physical unit that deﬁnes the main, or parent, population. A sin-

gle element of a sample is called an event.

Consistent with the above deﬁnitions of variables, some samples are:

Assigned radio frequencies of FM broadcast stations whose transmit-

ters are located in the state of Ohio.

Temperature readings at 1:00 P.M. local time last Wednesday at

various locations around the city of New York.

Minimum barometric-pressure levels at the centers of Atlantic

hurricanes during the decade 1991–2000.

Brightness levels of halogen bulbs in oﬃces in Minneapolis.

Sound-intensity levels of the electric vacuum cleaners used in all the

households in Rochester, Minnesota.

When a sample consists of the whole population, it is called a census. When

a sample consists of a subset of a population whose elements are chosen at

random, it is called a random sample.

RANDOM VARIABLE

A random variable is a discrete or continuous variable whose value cannot

be predicted in any given instance. Such a variable is usually deﬁned

within a certain range of values, such as 1 through 6 in the case of a

thrown die, or from 88 MHz to 108 MHz in the case of an FM broadcast

channel.

It is often possible to say, in a given scenario, that some values of a

random variable are more likely to turn up than others. In the case of a

thrown die, assuming the die is not ‘‘weighted,’’ all of the values 1 through 6

are equally likely to turn up. When considering the FM broadcast channels of

public radio stations, it is tempting to suppose (but this would have to be

conﬁrmed by observation) that transmissions are made more often at the

lower radio-frequency range than at the higher range. Perhaps you have

noticed that there is a greater concentration of public radio stations in the

4-MHz-wide sample from 88 MHz to 92 MHz than in, say, the equally wide

sample from 100 MHz to 104 MHz.

In order for a variable to be random, the only requirement is that it be

impossible to predict its value in any single instance. If you contemplate

throwing a die one time, you can’t predict how it will turn up. If you

contemplate throwing a dart one time at a map of the United States while

wearing a blindfold, you have no way of knowing, in advance, the lowest

radio frequency of all the FM broadcast stations in the town nearest the

point where the dart will hit.

CHAPTER 7 A Statistics Sampler 147

FREQUENCY

The frequency of a particular outcome (result) of an event is the number

of times that outcome occurs within a speciﬁc sample of a population.

Don’t confuse this with radio broadcast or computer processor frequencies!

In statistics, the term ‘‘frequency’’ means ‘‘often-ness.’’ There are two species

of statistical frequency: absolute frequency and relative frequency.

Suppose you toss a die 6000 times. If the die is not ‘‘weighted,’’ you should

expect that the die will turn up showing one dot approximately 1000 times,

two dots approximately 1000 times, and so on, up to six dots approximately

1000 times. The absolute frequency in such an experiment is therefore

approximately 1000 for each face of the die. The relative frequency for

each of the six faces is approximately 1 in 6, which is equivalent to about

16.67%.

PARAMETER

A speciﬁc, well-deﬁned characteristic of a population is known as a parameter

of that population. We might want to know such parameters as the follow-

ing, concerning the populations mentioned above:

The most popular assigned FM broadcast frequency in the United

States.

The highest temperature reading in the city of New York as determined

at hourly intervals last Wednesday.

The average minimum barometric-pressure level or measurement at the

centers of all the hurricanes in recorded history.

The lowest brightness level found in all the light bulbs in oﬃces in

Minneapolis.

The highest sound-intensity level found in all the electric vacuum

cleaners used in the world.

STATISTIC

A speciﬁc characteristic of a sample is called a statistic of that sample.

We might want to know such statistics as these, concerning the samples

mentioned above:

The most popular assigned frequency for FM broadcast stations in

Ohio.

The highest temperature reading at 1:00 P.M. local time last

Wednesday in New York.

PART 2 Finding Unknowns

148

The average minimum barometric-pressure level or measurement at

the centers of Atlantic hurricanes during the decade 1991–2000.

The lowest brightness level found in all the halogen bulbs in oﬃces

in Minneapolis.

The highest sound-intensity level found in electric vacuum cleaners

used in households in Rochester, Minnesota.

Distributions

A distribution is a description of the set of possible values that a random vari-

able can take. This can be done by noting the absolute or relative frequency.

A distribution can be illustrated in terms of a table, or in terms of a graph.

DISCRETE VERSUS CONTINUOUS

Table 7-1 shows the results of a single, hypothetical experiment in which a

die is tossed 6000 times. Figure 7-3 is a vertical bar graph showing the

same data as Table 7-1. Both the table and the graph are distributions that

describe the behavior of the die. If the experiment is repeated, the results

will diﬀer. If a huge number of experiments is carried out, assuming the

die is not ‘‘weighted,’’ the relative frequency of each face (number) turning

up will approach 1 in 6, or approximately 16.67%.

Table 7-1 Results of a single, hypothetical experiment

in which an ‘‘unweighted’’ die is tossed 6000 times.

Face of die Number of times face turns up

1 968

2 1027

3 1018

4 996

5 1007

6 984

CHAPTER 7 A Statistics Sampler 149

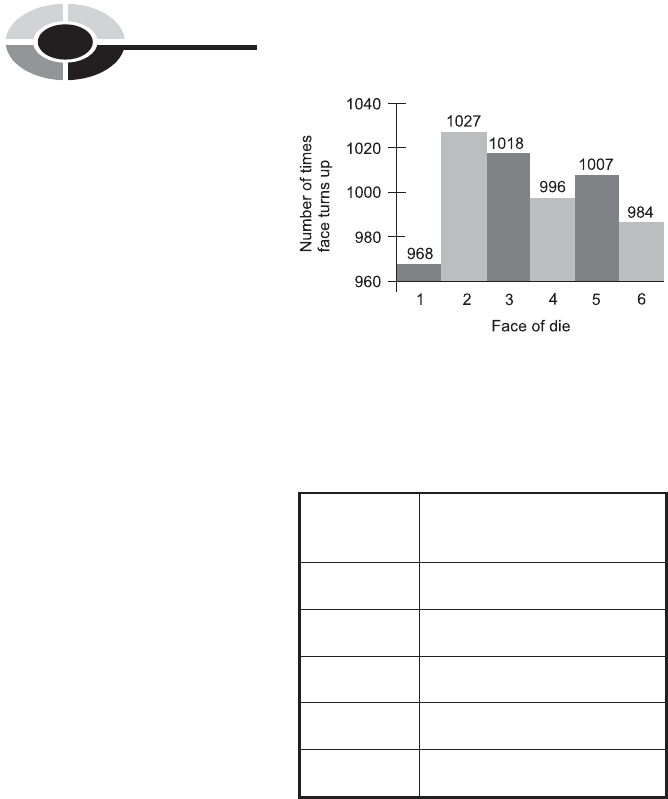
Table 7-2 shows the number of days during the course of a 365-day year in

which measurable precipitation occurs within the city limits of ﬁve diﬀerent

hypothetical towns. Figure 7-4 is a horizontal bar graph showing the same

data as Table 7-2. Again, both the table and the graph are distributions.

If the same experiment were carried out for several years in a row, the results

would diﬀer from year to year. Over a period of many years, the relative fre-

quencies would converge towards certain values, although long-term climate

change might have eﬀects not predictable or knowable in our lifetimes.

Both of the preceding examples involve discrete variables. When

a distribution is shown for a continuous variable, a graph must be used.

Figure 7-5 is a distribution that denotes the relative amount of energy

available from sunlight, per day during the course of a calendar year, at a

hypothetical city in the northern hemisphere.

Fig. 7-3. Results of a single, hypothetical experiment in which an ‘‘unweighted’’ die is tossed

6000 times.

Table 7-2 Number of days on which measurable rain

occurs in a speciﬁc year, in ﬁve hypothetical towns.

Town name Number of days in year

with measurable precipitation

Happyville 108

Joytown 86

Wonderdale 198

Sunnywater 259

Rainy Glen 18

PART 2 Finding Unknowns

150