Glikin A.E. Polymineral-Metasomatic Crystallogenesis

Подождите немного. Документ загружается.

212 5 Metasomatic Transformation of Aggregates

5.3.3 General Regularities and Possible Mechanisms

The results obtained are too incoherent to allow development of a unified theory of

recrystallizations in solutions. However, some fundamental tendencies can be

briefly summarized as follows.

Activity and passivity are the main peculiarities of mixture aggregates, which are

recrystallized under thermo-oscillation conditions. Active aggregates undergo sig-

nificant fast changes and passive ones preserve basic elements of initial structure

for a long period of time.

A mixture of NaNO

and K

can be an example of an active aggregate,

because the time required for a complete transformation of its macrostructure varies

depending on composition from several weeks to several months (Figs. 5.15 and

5.16). A mixture of KCl and K

is an example of a passive aggregate, because

its macrostructure does not significantly alter for at least 2 years.

The following mixtures NaNO

–K

, Ba(NO

)

–BaCl

·2H

O, and

KAl(SO

)

·12H

O–NiSO

·7H

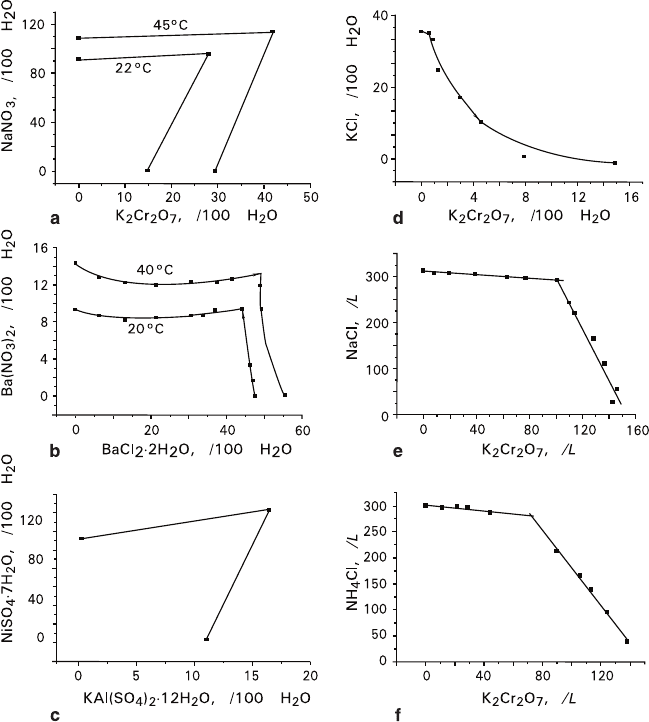
O were active in all studied experimental series (Fig.

5.13a–c). For each mixture there is an extreme content of a component, and if a

content of the component exceeds the extreme value, the mixture separates into a

monomineral part and bimineral part. The compositions of bimineral parts do not

depend upon the initial aggregate compositions. As a whole, quantitative character-

istics of transformed aggregates are almost unaffected by the temperature condi-

tions and sizes of the initial fractions.

On the contrary, there are not any extreme contents for mixtures of NaCl and

(in majority of series) and NH

Cl–K

(at 21°C), or they are indis-

tinct, while bimineral parts form almost the same compositions at various compo-

nent ratios of the initial mixtures (Figs. 5.13d, e). These mixtures, and also

KCl–K

mixture, can be classified as passive ones, though under certain con-

ditions they can behave as active systems.

Despite a wide spread of the experimental points and incompleteness of the data

obtained for different mixtures, some other tendencies can be derived from Fig.

5.13. In each case, high-temperature conditions (42°C) cause more intensive sepa-

ration into layers in comparison with that observed in the low-temperature mode

(21°C). This tendency is more expressed in the passive mixtures (5.13d, e) than in

the active ones (5.13b). Increase of the fraction content also leads to more intensive

separation, which appears to be significant in the passive mixture (5.13d), and vis-

ible in the active mixtures (5.13b, c).

Activity and passivity of mixtures is regarded as the system belonging to the

particular type with “salting-in” and “salting-out” respectively (Glikin et al. 1988;

Petrov et al. 1988; Glikin 1991; Glikin and Petrov 1998; see Sects. 1.5.1 and 4.1).

Comparison of data obtained for capabilities of certain mixtures to undergo

recrystallization with the data available on phase equilibria (Figs. 5.13 and 5.21)

shows that the active systems studied belong to the type “with salting-in” (Figs.

5.21a–c) either in the whole compositional range of saturated solutions (NaNO

–

–H

O and KAl(SO

)

·12H

O–NiSO

·7H

O–H

O), or at least for composi-

tions, which are close to their eutonic points (Ba(NO

)

–BaCl

·2H

O–H

O). On the

contrary, passive systems KCl–K

–H

O, NaCl–K

–H

O, and NH

Cl–

–H

O belong to the type “with salting-out” (Figs. 5.21d–f).

Positive feedbacks act in the active mixtures ensuring maximal rates and effi-

ciency of recrystallization due to salting-in effect. Elevation of temperature

Fig. 5.21 Phase concentration diagrams of active (a–c) and inert (d–f) systems: Data for NaNO

–

–H

O and KAl(SO

)

·12H

O–NiSO

·7H

O–H

O systems were provided by Dr S. V.

Petrov, data for Ba(NO

)

–BaCl

·2H

O–H

O, KCl–K

–H

O, NaCl–K

–H

O, and

Cl–K

–H

O systems were taken from Solubility (1961–1970). Isotherms for systems

(c–f) 20°C

ggg

5.3 Recrystallization of Polymineral Aggregates 213

214 5 Metasomatic Transformation of Aggregates

increases dissolution rate of each component due to salting-in effect of the dissolv-

ing partner component which goes into solution. Similarly, lowering the tempera-

ture accelerates precipitation of each component due to diminishing the concentration

of the partner component.

Passive mixtures form negative feedbacks, which slow down recrystallization

process due to salting-out effect. Elevation of temperature slows down dissolution

of each component due to salting-out influence of the partner component, which

dissolves. Analogously, lowering the temperature causes slowing down of the pre-

cipitation of each component as a result of the decrease in the partner component

concentration.

The feedback efficiency obviously weakens with increase of distances between

the crystals of different phases, since the time necessary for saturation of a great

volume of solution and transportation of substance to partner-crystal increases. It

can be seen as reduced passivity of NaCl–K

mixtures containing fractions of

greater sizes and, correspondingly, greater intercrystalline intervals (Fig. 5.13d).

However, changes observed in active Ba(NO

)

–BaCl

·2H

O and KAl(SO

)

·12H

O–

NiSO

·7H

O mixtures (Figs. 5.13b, c) are opposite to the expected.

Diminishing passivity of NaCl–K

mixture and increasing activity of

Ba(NO

)

–BaCl

·2H

O mixture with elevation of temperature and transition from

the low-temperature to high-temperature mode can be induced not only by change

of the absolute temperature, but also by alteration of the amplitude of oscillating

temperature perturbation.

System of NH

Cl–K

O–H

O is a system with salting-out, but separation of the

corresponding mixture into layers is rather fast. In a low-temperature mode (21°C,

0.25–0.5 mm fraction) it behaves similar to a passive NaCl–K

O mixture capable

of layering (high-temperature mode 42°C, 0.5–1 mm fraction). Probably, different

conditions compensate the differences in properties of the systems, and the processes

eventually lead to similar results. In a high-temperature mode, NH

Cl–K

O–H

behaves as a typical active mixture, but this can be a result of an equilibrium trans-

formation occurring above 40°C and the system conversion into a KCl–Na

–

O mixture.

Probably, in contrast to low-temperature conditions, the resulting

system is a system with salting-in; moreover, transition from one state to another

should be accompanied by a metasomatic transformation of the mixture phase com-

position, which would profoundly affect the process of recrystallization (especially

if the transition point lies within the interval of the temperature oscillations).

Such conversion remains unfortunately uninvestigated despite the fact that it frequently occurs in

complex systems. Representative examples of the systems comprise a phthalate mixture KHC

–

·4C

·4H

O–H

O (Fig. 7.13). For this system the eutonic line intersects the line of the

solution composition stoichiometric in respect to KHC

in the area located between the regions

of KHC

and K

·4C

·4H

O. That results in alterations in the composition of the

phase undergoing crystallization occurring in accordance with the change in temperature. To prevent

this alteration it is necessary to add KOH into solution (Glikin et al. 1979).

Variety of curve types plotted for passive mixtures and similarity of dependencies

drawn for active systems indicates a greater sensitivity of the negative and less sus-

ceptibility of the positive feedbacks to various factors of the process. The conclusion

seems quite logical as variations of multidirectional factors can lead to the qualitative

changes in the process taking place in passive mixtures, while variations of unidirec-

tional factors in active mixtures change only their quantitative characteristics.

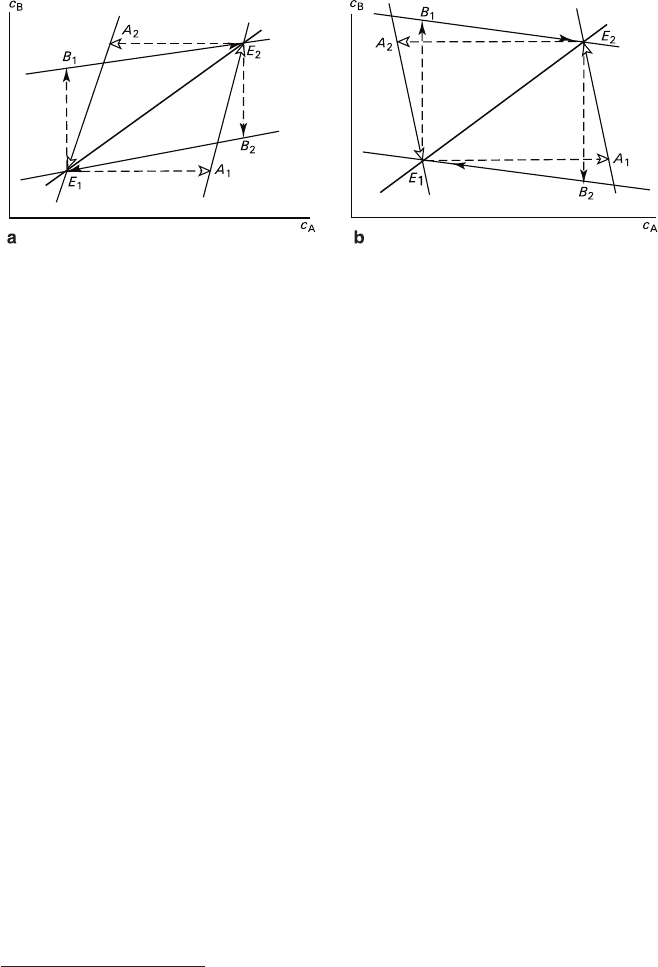
A physicochemical aspect of recrystallization in systems of main types having

fixed phase compositions

and positive temperature gradients of solubilities is sche-

matically shown in Fig. 5.22. The temperature varies within the range T

–T

cor-

responding to the solubility isotherms containing eutonic points E

and E

. The

mixture contains excesses of both crystal phases, which exceed fluctuations of their

contents in solution induced by changes of temperature.

At elevating temperature the total solution compositions in any systems move

from the neighborhood of the eutonic points E

to the neighborhood of E

along an

arbitrary trajectory lying within the limits of quadrangles E

. The trajectory is

determined by the dissolution rates of different phases and elevation of temperature.

If the temperature rises sufficiently slowly, the equilibrium dissolution takes place

and the trajectory coincides with the eutonic line. The trajectory of a nonequilibrium

process depends upon a ratio between the rates v of solution saturation with compo-

nents A and B; the difference in values v can be determined by differences in dissolu-

tion kinetics and the sizes of crystals formed by different phases. The extreme

trajectories are lines E

or E

(if v

< v

or v

> v

, respectively). If v

and v

Recrystallization of mixtures containing isomorphic components cannot be discussed at present.

Preliminary investigations gave ambiguous results ranging from a complete passivity to an active

separation of system into layers. This can be accounted for by a great complexity of crystalloge-

netic processes proceeding in the systems, which at the present state-of-the-art makes any predic-

tions impossible.

Fig. 5.22

Changes in total compositions of solutions during recrystallization of active bimineral

mixtures with salting-in (a) and passive bimineral mixtures with salting-out (b): E

–E

–

equilibrium trajectories at lowering or elevating temperatures, E

–E

or E

–E

– extreme nonequilibrium trajectories

5.3 Recrystallization of Polymineral Aggregates 215

216 5 Metasomatic Transformation of Aggregates

are of the same order of magnitude, the intermediate trajectories lie within E

regions, and their extreme points may or may not coincide with E

and E

At lowering temperature the total solution compositions change in the opposite

direction (from the neighborhood of E

to the neighborhood of E

) and within the

limits of other quadrangles: E

. If the temperature lowering is sufficiently

slow, the composition trajectory of the solution undergoing equilibrium crystalliza-

tion of both phases accompanied by the solution depletion coincides with the

eutonic line in the way similar to the dissolution stage. The extreme trajectories of

nonequilibrium processes are E

(if v

< v

) or E

(if v

> v

), whereas the

intermediate trajectories lie within the areas E

or E

. Nonequilibrium

trajectories for the stages corresponding to elevation of temperature and its lower-

ing lie on the opposite sides of the eutonic lines.

The shapes of trajectories of the processes occurring in the systems with salting-in

and salting-out (Figs. 5.22a and 5.22b respectively) differ. The trajectories of the

former process (Fig. 5.22a) always have positive values of ∂c

/∂c

regardless to

elevation or lowering the temperature. For the latter system (Fig. 5.22b) the sign of

the derivative can change, for example, on the extreme trajectories in the points A

and B

at increasing temperature and in the points A

and B

at lowering temperature;

the course of process after a change of the sign corresponds to a metasomatic

salting-out reaction, which impedes the process.

It should be noted that physicochemical scheme described covers variations of

the total solution composition and is intended for providing an explanation for

activity and passivity of polymineral mixtures undergoing recrystallization.

Three-stage division of thermo-oscillatory recrystallization of active mixtures is

the next important feature of the process which terminates by the aggregate, reach-

ing a stationary state with respect to the macrostructure, granulometric, and mineral

composition (Figs. 5.12, 5.15, and 5.16). The three-stage sequence of monomineral

aggregate recrystallization was in general described as resulting from a superposi-

tion of several competing mechanisms (Askhabov 1984). The results presented

allow to conclude that all the recrystallization processes involve a participation of

a three-stage mechanism, which can be further adjusted to describe the processes

occurring in polymineral aggregates.

The mechanism suggested below for polymineral recrystallization is considered

(Glikin 1991; Glikin and Petrov 1998) as generalization of a model proposed for

monomineral recrystallization, which is based on cyclic alternations of processes of

dissolution and growth of grains and takes into consideration essential differences

in rate disorders of the growth and dissolution processes (Punin 1965). The process

in question is characterized by a high structural stability of the final aggregate,

abrupt transitions between the stages, and fast termination of layering caused by

changes in ratios between the solid phases. Heterogeneous distribution of crystals

by imperfection, which determines monomineral recrystallization (Punin 1965),

cannot explain these phenomena.

The major factor of polymineral recrystallization is considered to be heterogene-

ous and nonoptimal spatial distribution of crystals belonging to different phases and

having various sizes. In general, it is distribution of crystals having different proper-

ties, and then monomineral recrystallization appears to be a particular case of the

process. In accordance with the mechanism suggested by Krasnova and co-workers

(1985), temperature fluctuations result in solution enrichment or depletion with

different components in various points (during dissolution or growth of the aggre-

gate crystals, correspondingly), thus acquiring concentration heterogeneity. Light

and heavy portions of the solution migrate along the intergrain interstices upwards

and downwards. Crystallization of separated solutions at lowering temperature

leads to the layering of an aggregate.

The term “grain coordination” hereinafter means a number of grains of one

mineral surrounding a central grain composed of the other mineral (by analogy with

crystallochemical terminology) in a conventional “coordination cell.” The greater

the coordination number of a cell and, respectively, the smaller the sizes of coordi-

nating grains, the greater are their relative surfaces and the faster the concentration

of the grain substance varies under the action of the changing temperature in the

solution surrounding the central grain. Therefore, a greater coordination number is

the reason for a faster reaction of the central grain to the temperature change, as it

results from a faster saturation of the solution with the component of the substance

inducing salting-in. Heterogeneous structure of an aggregate defines various coor-

dination numbers for the grains of the same substance thus resulting in variations

of solution density from cell to cell.

This mechanism is also considered to be responsible for formation of the block

and layered heterogeneities in intermediate macrostructures of cumulative recrystal-

lization. According to it, polymineral ensembles initially enriched with some com-

pound are represented as the centers of “macrocells.” Each ensemble behaves as an

entity towards the medium (similarly to the dense aggregates of crystals during

metasomatic replacement), and “coordination cells” described above are formed

inside the ensembles. The cells promote dissociation of macroheterogeneities. If a

system contains large crystals, the kinetics of recrystallization changes (Fig. 5.16)

and that can also be explained as follows: these crystals act as “continuous macro-

cells,” and their dissociation can be induced only by resorption of external contours.

It explains formation of the above comb crystals (Fig. 5.17). Separation into layers

stops when the aggregate reaches a homogeneous composition.

Criteria of uniformity of the aggregate composition are absent. From the point

of view of the model discussed, the composition can be determined as homogene-

ous if the solution composition and density vary equally in all the coordination cells

under the action of temperature perturbations. This could be true if ensembles of

crystals forming the cells had definite combinations of geometrical characteristics

of individuals (shapes, sizes, and coordinations) ensuring identical responses of the

cells to perturbation. In some sense, such structure is so highly ordered that it disa-

grees with supposition of equilibrium systems losing perfection of mineral distribu-

tion (Aleksandrov 1995).

Universal approach to definitions of homogeneity and ordering in structures of polymineral

aggregates seems to be impossible, as impossible is creation of a universal classification.

5.3 Recrystallization of Polymineral Aggregates 217

218 5 Metasomatic Transformation of Aggregates

Another effective factor is apparently a degree of system deviation from the

equilibrium during dissolution or growth. At increasing temperature rates, increas-

ing the concentrations of both substances can be arbitrary (Fig. 5.22a and com-

ments to it). Thus, if the dissolution rate of the component A is essentially greater,

there are no obstacles for solution composition to move along the trajectory

. On the contrary, the inverse symmetric change of solution composition

along the trajectory E

in accordance with a formal hysteresis principle is

apparently hampered, since growth of the crystals A should occur in a stability

domain of the phase B. Most likely, optimal aggregate composition is a composi-

tion, which counterbalances rates of dissolution and growth of both phases so that

change of solution composition during the temperature fluctuations occurs along

the eutonic line.

It is to be reminded that an important structural feature of a recrystallized

aggregate is its multimodal granulometric composition (Petrov et al. 1988).

Taking into consideration this experimental fact, it is possible to demonstrate

geometrically that one of the conditions of permanent-equilibrium state of an

aggregate under conditions of temperature oscillations should be optimal multi-

modal granulometric composition of the aggregate. An example of such a sys-

tem is an elementary case of monomineral ensemble consisting of i number of

grains having mass M and j number of grains having mass m (the total aggregate

mass is iM + jm). During dissolution the masses of corresponding grains

decrease by ΔM

−

and Δm

−

, while during growth, they increase by ΔM

and Δm

respectively. Maintaining the equilibrium should correspond to the following

condition: iΔM

−

+ jΔm

−

= iΔM

+ jΔm

, or i(ΔM

−

− ΔM

) = j(Δm

−

− Δm

); or:

i/j = (Δm

−

− Δm

)/(ΔM

−

− ΔM

). This example proves a possibility of reaching

the equilibrium state during a monomineral recrystallization. It can also at least

partially explain the experimental results showing granulometric multimodality

of these aggregates (Punin 1964) and slowing down the process at the final stage

(Askhabov 1984). Despite the obvious complexity of strict calculation, the

physical meaning of above formula must be applicable for polymineral aggre-

gates containing crystals of random shapes, including variants of variable

growth and dissolution rates.

Hence, stationary states of recrystallized aggregates having close granulometric

and mineral compositions, achieved irrespective to their initial compositions, can

be explained by formation of homogeneous structures providing conditions for

preservation of uniform structures ensuring local (for individual cells) and common

equilibrium between the aggregates and solution under the action of temperature

perturbations. However, a reason for a system to choose a direction of structural

transformation is still unclear. It is possible to assume that the basic role belongs to

asymmetry of trajectories defining movement from E

to E

and back (Fig. 5.22),

which disappears when they merge with the eutonic line: as mentioned earlier, dis-

solution trajectory can be arbitrary, while configuration of the growth trajectory

should be delimited, since, in general, the components crystallize within a “for-

eign” domain. Solution of this problem requires experimental or at least physico-

chemical computer examination of the sites located around separate grains and

analysis of the system evolution caused by interactions of different sites of this

liquid mosaic.

Among the other mechanisms leading to a stationary condition, it is necessary

to mention plugging of intergrain interstices as a result of the aggregate condensa-

tion, and slowing down the alternating processes of saturation–depletion of the

solution caused by reduction in dispersivity of the aggregate. They should induce a

gradual change of the process rate, and, probably, these mechanisms prevail in the

course of separation of passive NaCl–K

mixtures into layers (at 42°C, see

Figs. 5.13d, e).

All the information stated above allows the following assumptions concerning

the nature of recrystallization stage to be made. Incubation interval I (Fig. 5.15) is

determined by isolation of those coordination cells or their ensembles in which

deviations of concentration from the average induced by temperature changes are

most significant. The active stage A comprises convective infiltration of light and

heavy portions of solution through the aggregate mass, decomposition of cells

whose kinetic parameters significantly deviate from the average values, and forma-

tion of new cells with approximately average characteristics. The stationary stage S

includes self-regulation of structure to acquire an optimum-homogeneous distribu-

tion of the crystal phase.

Quantitative estimation of the individual process components determining the

composition of recrystallized aggregates was performed by S. V. Petrov and G. N.

Polishchuk (Petrov et al. 1988). Five major components covering about 80% of the

total dispersion of attributes (the remaining 20% cover the components of small

importance) were determined using R-modification of factor analysis, which

included:

1. Crystal coarsening accompanied by phase redistributions (45%)

2. Transformation of monomodal grain-size distribution into a multimodal distri-

bution (13%)

3. Profound heterogeneity of initial granulometric composition (10%)

4. Formation of metacrystals (6%)

5. Increase of the average grain size in the column in downward direction (6%)

Change of grain size accompanies recrystallization of aggregates in the form of

either coarsening or reduction.

Grain coarsening is considered as one of the basic characteristics of the process

(Grigor’ev 1961; Punin 1964; Grigor’ev and Zhabin 1975; Askhabov 1984; and others).

Our experiments show that granulometric effects of recrystallization of the active

polymineral mixtures are similar to those observed in monomineral aggregates and

include statistical grain coarsening, multimodal size distribution, and a three-stage

process. However, these effects are different in their nature. In monomineral process

the leading factors are heterogeneous distribution of crystals according to their

imperfection (Punin 1965) and the crystal sizes (Gordeeva and Shubnikov 1967;

Vacek et al. 1975a, b). In polymineral process, the leading role is believed to belong

to heterogeneity of spatial distribution of solid components and to physicochemical

parameters of the solution, which were discussed above in the present section.

5.3 Recrystallization of Polymineral Aggregates 219

220 5 Metasomatic Transformation of Aggregates

Grain reduction seems to be unusual process; we observed it during polymineral

recrystallization and consider it to be induced by its metasomatic component.

Two types of processes take place in active mixtures (see Sect. 5.3.1): fragmen-

tation of the large crystals surrounded by the fine-grained aggregate of the other

substance (formation of druse cavities, and also, probably, the comb crystals; see

Fig. 5.17), and development of net fine-grained ensembles of one substance along

the intergrain borders of the other (Fig. 5.14). We consider both processes to be

examples of formation of Type II negative replacement products due to salting-in

at lowering temperature (see Sects. 1.2, 1.4, and 1.5.1).

Grain fragmentation seems to be usual enough for passive mixtures. It can be

logically deduced from a significant role the metasomatic stage plays in the mecha-

nism ensuring mixture passivity (Fig. 5.22b and comments to it), as, according to

conclusions presented in Sect. 1.5.1, replacement of Type Ia results in polycrystal-

line replacement.

We observed a special case of recrystallization proceeding according to a meta-

somatic mechanism involving the grain fragmentation in passive NaCl–KCl mix-

ture, which does not undergo layering. In this system, fragmentation of aggregates

occurs along the intergrain borders; it is shown in Fig. 5.19. It is defined by

“inverted” eutonic line determined by significant difference in the temperature

solubility gradients (Glikin 1996a) (Figs. 2.8a and 4.1i and explanations given in

Sects. 2.2 and 4.4). At fluctuating temperatures the process proceeds in cyclic mode

from the neighborhood of E

to the neighborhood of E

and vice versa. Each stage

includes dissolution of one phase and growth of the other, and their change leads to

inversion of the phase functions, i.e., the replacing phase becomes a phase undergo-

ing replacement and vice versa.

This type of replacement results in formation of polycrystalline products, and

the process includes a stage of nucleation, which requires at least a minimal

supersaturation. After precipitation of a sufficient amount of a fine-grained frac-

tion, which has high specific surface, supersaturation abruptly slows down as

temperature drops, and subsequent nucleation does not occur. Fragmentation

stops, and the process turns into its slow stage. The trajectory of figurative point

during this process apparently coincides with the eutonics. Short duration of the

experiments does not allow to define whether this stage is stationary or if it is a

preliminary stage for a subsequent gradual evening-out of grain-size distribution.

It is interesting to note that such stationary state is quite possible; in this case, the

resulting structure consisting of a large and fine crystal mixture should be consid-

ered homogeneous in accordance with our definition mentioned in this section.

Classification of mixtures in accordance with their thermo-oscillatory recrystal-

lization ability, as well as division of crystals in accordance with their susceptibility

to isothermal metasomatic replacement is determined by physicochemical types of

We do not speak of a trivial variant, which is diminishing the grain sizes in some fraction of an

aggregate due to coarsening of the others.

corresponding systems. It should be noted that recrystallization proceeds in systems

with salting-in, and metasomatic replacement, on the contrary, takes place in sys-

tems with salting-out.

Passivity of a mixture is rather a conditional concept describing relative stability

of its macrostructure in the course of thermo-oscillatory recrystallization; in sys-

tems of this type, intensive processes proceed at the level of individuals or even at

a macrostructural level if temperature gradients exist in the system.

Thermogradient recrystallization phenomena complete the schematic picture of

the fourth class of overelementary metasomatic processes (see Introduction). The

main tendencies are described briefly as follows.

Different mixtures are transformed into columns having similar macrostructures

and containing a central druse cavity and a series of layers differing partially or

entirely in their mineral composition and divided, as a rule, by sharp borders, which

are perpendicular to the temperature gradient (Fig. 5.20). The most important fact

is that the resulting structure does not depend upon the system belonging to one of

the above types, i.e., with salting-in or salting-out. Therefore, it can be concluded

that mechanisms of thermogradient and thermo-oscillatory recrystallizations are

different.

Thermogradient columns have at least three characteristic features. The first

one is a central druse cavity appearing as a result of contraction due to condensa-

tion of near-selvage zones; they are likely to bear a genetic similarity to the axial

cavities in the alpine veins. The second feature is asymmetry of the upper and

lower zoned structures determined by gravitation factor. The asymmetry shows in

vertical crystal bunches, breaking the sharpness of contacts that confirms existence

of concentration flows, similar to the flows causing layering of aggregates during

thermo-oscillation processes (see this Section). The third peculiarity consists in

the presence of large metacrystals both in the druse cavity and the fine-grained

matrix of the partner component. These formations are results of convective mass

transfer (so-called autoclave effect) and can assist in distinguishing recrystalliza-

tion from thermo-oscillation recrystallization, provided they do not occur

simultaneously.

Judging from the signs mentioned above and microstructural attributes, the

resulting columns (Fig. 5.20) can be considered to be identical to experimental

metasomatic or bimetasomatic columns (Zaraiskii 1979, 1991; Zaraiskii et al.

1986). Photos and drawings presented in the cited publications allow to draw right-

ful analogies. The common feature is also a gradual extinction of the processes with

time. These similarities indicate identity of the both recrystallization mechanisms,

and thus, evolution of thermogradient recrystallization columns is determined by

differential mobility of the components participating in the process and by local

equilibrium in various column zones, which is in a good agreement with theory of

metasomatic zonality (Korzhinskii 1970, 1993). Classical processes and the proc-

esses described above differ in driving forces – concentration and temperature

gradients, respectively – and this difference can be easily included in theoretical

basis of the cited works.

5.3 Recrystallization of Polymineral Aggregates 221