Gross R., Sidorenko A., Tagirov L. Nanoscale Devices

Подождите немного. Документ загружается.

74 Rudolf Gross

by the heavy, whereas P

Nv²

and P

tun

are determined by the light electrons.

That means, that P

DOS

and P

Nv²

or P

tun

can be very different, since they are

determined by different types of electrons. Moreover, P

DOS

and P

Nv²

or P

tun

can have opposite sign. A typical example for this second case is Ni.

Although band structure calculations yield P

DOS

< 0 for Ni, the transport

spin polarization has opposite sign for a large energy range, i.e. P

Nv²

> 0.

Indeed, for Ni usually a positive spin polarization is derived from transport

experiments, where P

Nv²

is measured, which is however much larger than

expected from band structure calculations. This indicates that band structure

calculations underestimate the effect. This most likely is due to the fact that

band structure calculations yield a too weak localization of the d-electrons.

Classification of half-metals

In this subsection we give a classification of half-metals using the

definitions for the spin-polarization given above. Doing so, we will follow

Coey's work [151, 152]. Usually, a half-metal is defined as a material which

is a normal metal with a well-defined Fermi surface for one spin direction,

but shows a gap in the density of states around the Fermi level for the other

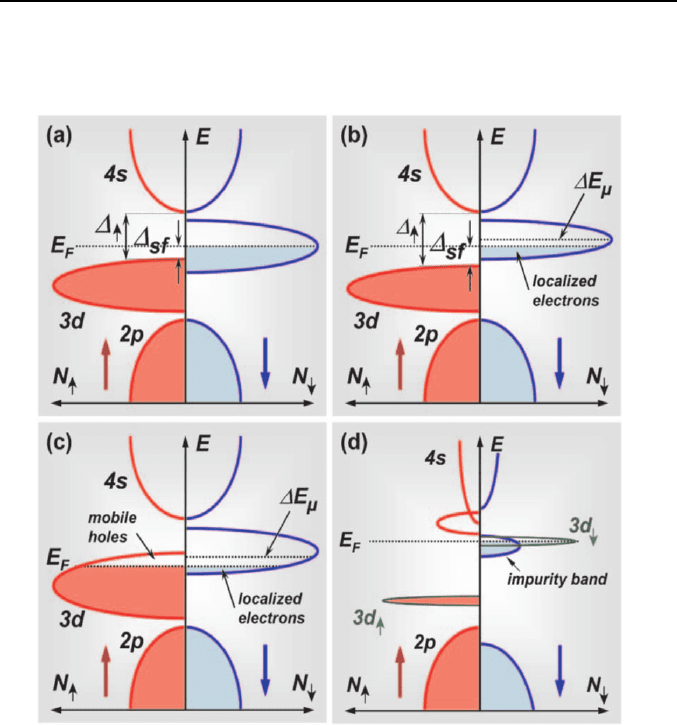
spin direction [153]. This classical definition is shown in Fig. 6a. Following

Coey we denote these half-metals as type-I half-metals. A further

classification into

and I

can be made depending on whether there are

less or more than five d electrons so that either the spin-up or spin-down

band is only partly filled. In either case there is a spin gap ∆

↑

or ∆

↓

and a

smaller gap ∆

for spin-flip excitations (see Fig. 6a).

It is well known that ferromagnetic transition metals are no half-metals.

Although e.g. Co and Ni have a d-band split so that all 3d

↑

subbands are

filled and only the 3d

↓

subbands cross the Fermi level, the presence of an

unsplit 4s conduction band results in a finite density of states for both spin

directions at the Fermi level. A half-metallic behavior can be generated by

shifting upwards the 4s band. In oxides this is achieved by the hybridization

of the 4s metal and the 2p oxygen states pushing the 4s band up above E

or shifting down the Fermi level into the d band below the bottom of the 4s

band. Typical type-I half-metals are the transition metal oxides CrO

)

and double perovskites such as Sr

FeMoO

). Another well-known

example are the so called Heusler compounds. Here, heavy d elements such

as Sb tend to suppress the 3d levels below the 4s band edge by p-d

hybridization. For example, in NiMnSb [154] there are spin-up electron

with Ni e

character at E

(type I

). In contrast, in the compound Mn

VAl

[155] there are Mn t

spin-down electrons at E

(type I

). It is evident that

according to the different definitions of the degree of spin polarization

Magnetic Tunnel Junctions Based on Half-Metallic Oxides 75

given above, for type-I half-metals we have P

DOS

= P

Nv²

= P

tun

= 1.

That is, we have 100% spin-polarization independent of the specific

definition of the spin-polarization.

Fig. 6.

Schematic sketch of the densities of states for the spin-up and spin-down

electrons for the classification of different types of half-metals. For the type-I half-

metals, there is a finite density of states only for the majority, spin-up (not shown)

or minority, spin-down electrons (a), whereas there is a gap in the density of states

for the other spin direction. Type-II half-metals (b) are equivalent to type-I half-

metals. However, due to narrow bands the states at the Fermi level are localized

and transport is due activation across a mobility edge

∆E

. Finally, type-III half-

metals (c) have mobil charge carries for one spin direction and localized ones for

the opposite.

∆

↑,↓

is the representing the gap for a particular spin direction and ∆

is the gap for spin-flip processes. (d) shows a half-metal as expected from the spin-

split impurity band model [157], which describes the magnetic exchange in a high-

κ oxide (e.g. ZnO) doped with transition metal ions (e.g. Co) far below the

percolation threshold.

76 Rudolf Gross

Note that the d-bands may be very narrow. Then, in oxides the charge

carriers often form small polarons with large effective mass and small

mobility. Conduction is then by polaron hopping. Also, if the Fermi level is

close to the bottom or the top of the conduction band, disorder may cause

localization below or above a mobility edge. According Coey's

classification scheme, type-I half metals with localized charge carriers are

denoted as type-II half-metals (Fig. 6b). Again we can further subdivide

into type II

and II

depending on whether the band is less or more than

half filled. Obviously, we have P

DOS

= P

Nv²

= P

tun

= 1 also for type-II

half-metals. A typical candidate for a type- II

half-metal is magnetite for

which the Fermi level is in the

↓

band of octahedral iron. The charge

carriers of this band are localized to form polarons.

The strong localization of charge carriers in oxides brings us to the

definition of type-III half-metals (Fig. 6c). In such half-metals we have a

finite density of states at the Fermi level for both spin directions. However,

whereas the charge carriers for one spin direction are mobile, those for the

other are localized and cannot contribute to transport. Then, we have a half-

metal in the sense that we have metallic behavior for one and insulating

behavior for the other spin direction, i.e. again only half of the electrons

contribute to transport. A typical example for a type- III

half-metal is

0.7

0.3

MnO

with mobile Mn e

spin-up electrons and localized Mn t

spin-down electrons at E

. With respect to the different definitions of the

degree of spin polarization given above, for type-III half-metals we have

DOS

< 0, that is, the DOS spin polarization is less than 100%, it even may

be zero. However, since the charge carriers for one spin direction are

localized (e.g. v

↓

= 0), we have P

= P

Nv²

= P

tun

= 1. That is, the transport

spin polarization is 100%. This means that also type-III half-metals have

full spin-polarization for the majority of situations, where transport

properties are relevant.

As the last type we consider diluted ferromagnetic semiconductors. On

the

one hand, these materials can become ferromagnetic by a polarization

of the spins s of the conduction or valance band carriers due to the spin S of

localized ion cores by an s·S exchange. This exchange can cause a spin

splitting which is larger than the Fermi energy. Examples are (GaMn)As,

where the S = 5/2 core spin of the Mn

(3d

) ions split the top of the

valence band producing spin-down holes [156], and EuO or EuS doped

with trivalent rare earth elements. On the other hand, ferromagnetism can

arise from the fact that the dopant impurity atoms are sufficiently close to

form a narrow impurity band, which is unstable with respect to spin

splitting. Possible candidates for this category, where none of the atoms

needs to be magnetic, are (LaCa)B

and ferromagnetic carbon. Another

possibility

is that the ferromagnetic exchange is mediated by charge

Magnetic Tunnel Junctions Based on Half-Metallic Oxides 77

carriers in a spin-split impurity band [157]. Such spin-split impurity band

model can account for ferromagnetism in insulating or conducting high-κ

oxides with concentrations of magnetic transition metal ions that lie far

below the percolation threshold (Fig. 6d).

Measurement of spin polarization

The analysis given above makes clear that the spin polarization of a

material reported in the literature depends on the method used to measure it.

We therefore briefly summarize the various experimental methods sketched

in Fig. 7 and discuss the kind of spin polarization that is achieved.

Photoelectron spectroscopy

As illustrated in Fig. 7a, in spin-resolved photoemission experiments [158]

the surface of a material is irradiated by photons of energy ħω and the

photoelectrons emitted from the surface are analyzed using a spin-sensitive

detector (Mott analyzer) [159]. This method directly measures the DOS

spin polarization P

DOS

. However, it has several drawbacks. First, it is a

surface

sensitive method, since the emission depth of the photoelectrons is

Fig. 7. Illustration of different measuring methods for the spin polarization of

ferromagnets. (a) Spin-polarized photoemission from a ferromagnet upon

irradiation by photons of energy ħω (b) spin-polarized tunneling in magnetic tunnel

junctions, (c) spin-polarized tunneling in superconductor/insulator/ ferromagnet

(S/I/FM) tunnel junctions, (d) spin-polarized transport in point contacts between

two ferromagnets and (e) spin-polarized transport between a superconductor and a

ferromagnet involving Andreev reflection. H

ext

denotes the applied magnetic field,

M the magnetization in the ferromagnet, I

tun

the tunneling current and I the ballistic

or diffusive transport current in the point contacts.

78 Rudolf Gross

of the order of 10Ǻ. Therefore, the derived values of the spin polarization

are susceptible to surface states, reconstructions, contamination etc. Second,

the energy resolution is limited. Finally, in photoemission experiments the

spin polarization is usually measured only in a few k-directions and does

therefore not represent a Fermi surface average.

Superconducting tunnel junctions

The measurement of the spin polarization using a tunnel junction consisting

of a ferromagnetic and a superconducting electrode (see Fig. 7c) was

pioneered by Meservey and Tedrow [40, 44]. The tunneling conductance of

such junction is determined by the convolution of the density of states of

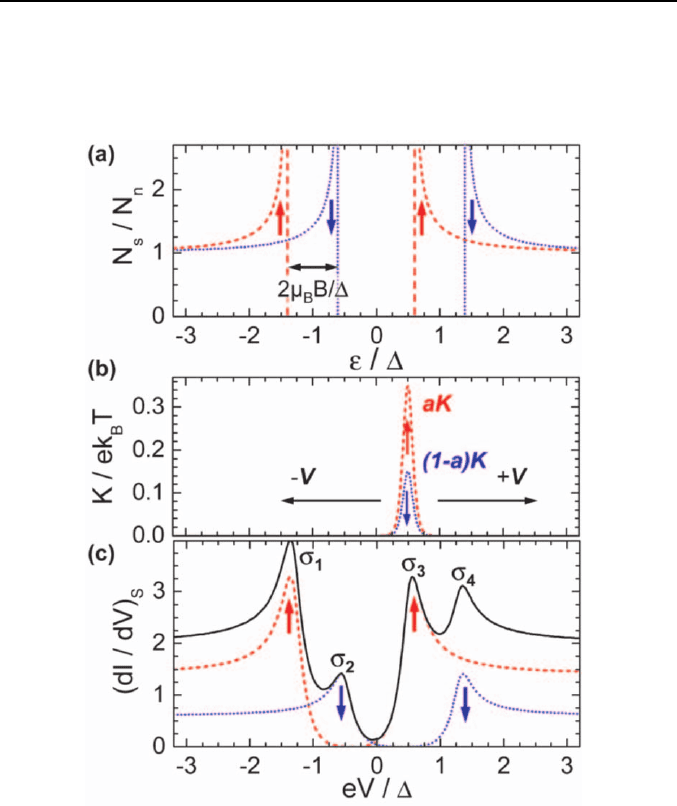
the ferromagnet and the superconductor. As illustrated in Fig. 8, the DOS of

the superconductor has a sharp peak at the gap energy ∆ and is symmetric

for spin-up and spin-down electrons. Applying a magnetic field parallel to

the junction electrodes this peak is spin-split by

B. The tunneling

conductance for the two spin direction is obtained by convoluting this split

DOS by the function aK and (1-a)K, where

)/(

↓↑↑

≡

NNNa

and

)/()(1

↓↑↓

+≡− NNNa

is the fraction of the spin-up and spin-down

electrons at the Fermi level in the ferromagnet and K is the derivative of the

Fermi function with respect to energy. Due to the finite spin polarization of

the ferromagnet we have a ≠ (1-a) and the conductance versus voltage

curves become asymmetric with four peaks at eV = ∆

B and eV = -∆

B as shown in Fig. 8. In a first approximation the spin polarization can be

evaluated by measuring the conductance values

at these peak

positions giving [44, 161]

,12=

)()(

3124

−

−+−

−

σσσσ

(44)

where the second equals sign is only correct, if the tunneling probability is

the same for the spin-up and spin-down electrons. In a more detailed

evaluation the measured conductance spectra have to be fitted to the

theoretical prediction using the spin polarization as fitting parameter and

taking into account spin-orbit and spin-flip scattering [161]. Note that spin-

orbit scattering is smearing out the Zeeman-split density of states while

magnetic impurities act as pair breakers and result in a reduction of the

energy gap.

In practice, usually Al is used for the superconducting

material,

since it has small spin-orbit scattering and its native oxide forms

a very good tunneling barrier. The drawback of this method is that it

requires very low temperatures (typically below 1 K) so that the spin-

Magnetic Tunnel Junctions Based on Half-Metallic Oxides 79

splitting 2µ

B of the superconducting DOS peak is larger than k

Therefore, it cannot be used to measure the temperature dependence of the

spin polarization. Recent experimental values are listed in Table 1.

Fig. 8. (a) Zeeman splitting of the DOS in a superconductor into spin-up (dashed)

and spin-down part (dotted) due to an applied magnetic field. (b) Energy derivative

K of the Fermi function for a specific voltage multiplied by the fraction a and (1-a)

of the spin-up and spin-down electrons at the Fermi level. (c) Spin-up (dashed) and

spin-down (dotted) conductivity vs voltage as well as the total conductivity (solid

line).

Although early experimental results have been interpreted in terms of

the DOS of the ferromagnetic electrodes, of course this method rather

yields the tunneling spin polarization P

tun

than P

DOS

. Indeed the

experimental values listed in Table 1 show that the spin polarization

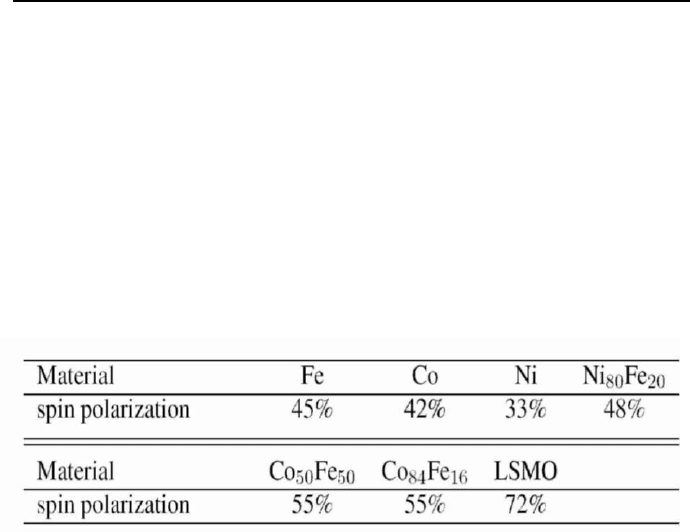
80 Rudolf Gross

determined according to eq. (44) is always positive for 3d transition metals

and alloys in obvious contradiction to band structure calculations [162],

which yield negative values for P

DOS

of Co and Ni. This contradiction was

first addressed by Stearns [74], who pointed out that for 3d transition metals

the tunneling current is dominated by the 4s electrons due to their small

effective mass and in turn large tunneling probability, whereas the DOS is

dominated by the 3d electrons. Taking this into account, a positive

tunneling spin polarization is obtained for Co and Ni in agreement with the

experiment.

with Al/AlO

/FM tunnel or Al/SrTiO

/FM (for FM = La

2/3

1/3

MnO

(LSMO))

junctions using equation (44) (data taken from Refs. [21, 44, 160, 161]).

Ferromagnetic point contacts. In point contacts or nano-constrictions

between two ferromagnets usually a contact area is formed that allows for

ballistic transport. Therefore, with such configuration the quantity P

can

be measured over a wide temperature range [163]. The drawback of this

technique is that in most cases there is a finite barrier strength Z or

equivalently a transmission probability T

< 1 of the contact. Furthermore,

usually both Z and the relative orientation of the two ferromagnets are not

precisely known. In most experiments this is circumvented by repeated

measurements with many contacts to obtain average results.

Point contact Andreev-reflection. If one part of the point contact is

replaced by a superconductor, the spin polarization of the ferromagnet can

be obtained by point contact Andreev spectroscopy [113, 114]. Andreev

scattering at a normal metal to superconductor (N/S) interface is caused by

the fact that electrons with energies smaller than the superconducting

energy gap cannot enter the superconductor due to the lack of available

states (see Fig. 9a). Therefore, an electron incident on the NS interface from

the N side is retro-reflected as a hole, while at the same time a singlet

Cooper pair formed by two electrons with opposite spin and wave vector is

Point contacts

Table 1. Spin polarization obtained from spin dependent tunneling experiments

Magnetic Tunnel Junctions Based on Half-Metallic Oxides 81

transferred to the superconductor [164]. That is, in total a charge of 2e is

transferred across the NS interface. As a result, the conductance is twice to

that of an N/N interface at bias within the gap. Andreev scattering is a

phase coherent scattering process and is responsible for the proximity effect

at N/S interfaces, where phase correlations are induced in the N material

[165, 166]. The situation changes for a ferromagnetic metal with finite spin

polarization. If P = 1, the Andreev reflection described above is completely

blocked. If an electron with wave vector k and spin-up is incident on the

FM/S interface, it requires an electron with wave vector -k and spin-down

to form a singlet Cooper pair and to enter the superconductor (formally, this

is equivalent to the retro-reflection of a spin-down hole, see Fig. 9b).

However, since for P = 1 such electrons are not available, this process is

blocked and the conductance is zero for bias within the gap [167].

In order to understand Andreev reflection at a FM/S interface we first

consider a FM/N interface. For a clean interface (Z = 0) the conduction at

zero bias, G(0), is given by

,)(=

↓↑

+ NN

(45)

that is, the conduction quantum times the number of contributing channels.

For a FM/S interface all the (minority) N

↓

but only the fraction (N

↓

↑

the (majority) N

↑

channels contribute to Andreev reflection and transfer the

charge 2e across the interface [113, 114]. This results in the conduction

,4=22=

↓↑

↑

↓













+ N

(46)

which would be zero for the situation shown in Fig. 9b. Normalizing to

FM/N

, we see that the suppression of the conductance at V = 0 and Z = 0

scales linearly with the spin polarization P of the ferromagnet as

[108, 113, 114]

,)(12=

(0)

−

(47)

82 Rudolf Gross

Fig. 9. Schematic illustration of Andreev scattering at (a) a normal

metal/superconductor (N/S) interfaces and (b) a ferromagnet/superconductor

(FM/S) interface. For simplicity in (b) a half-metal is assumed. The reflection of a

spin-down hole is forbidden in (b) due to lack of available states.

where G

FM/N

is the normal state conductance and the extracted spin

polarization is P = P

. For large barrier and/or diffusive transport the

extracted spin polarization is P = P

Nv²

in the first approximation. However,

for this case in general a more detailed analysis is required for exact results

[108]. Furthermore, for finite interface scattering (finite barrier strength Z)

the analysis of the experimental data is not as simple and one has to

determine the spin polarization by fitting the experimental conductance

versus voltage curve to model predictions incorporating interface scattering

[168]. Note that point contact Andreev reflection probes

〉〈

Nv averaged

over the entire Fermi surface, whereas tunneling through a thick barrier is

restricted to a narrow tunneling cone probing

Nv only at those selected

points of the Fermi surface, where quasimomentum is perpendicular to the

interface. However, the experimental data for the spin polarization obtained

from both methods are usually very close. The reason for that is the use of

polycrystalline materials in the tunneling experiments. Apparently,

averaging over individual grains helps to bring the tunneling spin-

polarization results close to the Fermi surface averaged point contact

Andreev reflection results [169].

Magnetic Tunnel Junctions Based on Half-Metallic Oxides 83

The advantage of the Andreev reflection technique is the detection of

spin polarization for a wider range of materials due to the simple sample

preparation. A large number of experimental results has been reported [167-

176]. Certainly, a drawback of the Andreev scattering method is that it can

be applied only at temperatures lower than the transition temperature of the

superconductor and therefore does not allow to determine the temperature

dependence of the spin polarization. Furthermore, care has to be taken in

the quantitative analysis of experimental data, which should take into

account factors such as an non-spherical Fermi surface [108] as well as the

roughness and size of the point contact leading to a diffusive component of

the transport [177-179].

Ferromagnetic tunnel junctions

For planar tunnel junctions formed by two ferromagnetic electrodes

separated by a thin insulating barrier the spin polarization can be

determined by measuring the resistance for parallel and anti-parallel

magnetization direction according to eqs. (2) and (3). However, as

thickness, defect states etc.). The quantity measured in such experiment is

usually the tunneling spin polarization P

tun

one has to distinguish between junctions with well oriented electrode and

barrier materials and those based on polycrystalline materials. As discussed

probability for junctions with

thick tunneling barrier only those electrons contribute significantly to the

tunneling conductance, which have the

smallest

, i.e. those with k

║

≈ 0.

Therefore, tunneling only probes certain crystallographic directions for oriented

electrode material. A Fermi surface average is only obtained for polycrystalline

electrodes due to the averaging

crystalline tunneling barriers can give rise

to a much higher tunneling spin polarization due to a highly spin-dependent

evanescent decay of the relevant wave functions [61, 62, 78]. That is, for single

crystalline or well a

oriented electrode material one has to take into account the

specific crystallographic orientation of the electrode material with respect to the

tunneling direction, whereas for polycrystalline electrodes one gets an

average over all possible orientations. In general, using planar MTJs it is

difficult to extract reliable information on the intrinsic DOS spin

polarization. However, the tunneling spin polarization obtained in

experiments based on MTJs is the quantity relevant for a large variety of

the electronic states at the interface and the choice of oxide barrier (height,

given by eq. (41). Furthermore,

discussed in the introduction the measured TMR values depend critically on

in the section on the tunneling definition of the spin polarization, due to the

dominating exponential factor in the tunneling

over many grains with different crystallo-

graphic orientation. Furthermore,

Gross R., Sidorenko A., Tagirov L. Nanoscale Devices - Fundamentals and Applications

Подождите немного. Документ загружается.