Gubbins D., Herrero-Bervera E. Encyclopedia of Geomagnetism and Paleomagnetism

Подождите немного. Документ загружается.

ranging to determine the vehicle’s position underwater. Once these

steps have been completed then the data can be treated like sea

surface data by removing the regional field to obtain an anomaly

and then calculating a source crustal magnetization.

Maurice A. Tivey

Bibliography

Cole, J.F., 1908. Magnetic declination and latitude observations in the

Bermudas. Terrestrial Magnetism and Atmospheric Electricity, 13:

49–56.

Dietz, R.S., 1961. Continent and ocean basin evolution by spreading

of the seafloor. Nature, 190: 854–857.

Glen, W., 1982. The Road to Jaramillo. Critical Years of the Revolution

in Earth Science. Stanford, CA: Stanford University Press, 459 pp.

Heezen, B.C., Ewing, M., and Miller, E.T., 1953. Trans-Atlantic pro-

file of total magnetic intensity and topography, Dakar to Barbados:

Deep Sea Research, 1:25–33.

Hess, H.H., 1962. History of ocean basins. In Engel, A.E.J., James,

H.L., and Leonard, B.F. (eds.), Petrologic Studies, the Burlington

Vo lu m e . Boulder, CO: Geological Society of America, pp. 599–620.

Johnson, H.P., Hautala, S.L., Tivey, M.A., Jones, C.D., Voight, J., Pruis,

M., Garcia-Berdeal, I., Gilbert, L.A., Bjorklund, T., Fredericks, W.,

Howland, J., Tsurumi, M., Kurakawa, T., Nakamura, K.,

O’Connell, K., Thomas, L., Bolton, S.,Turner, J., 2002. Survey stu-

dies hydrothermal circulation on the northern Juan de Fuca ridge.

EOS: Transactions of the American Geophysical Union, 83:73–79.

Macdonald, K.C., 1977. Near-bottom magnetic anomalies, asymmetric

spreading, oblique spreading, and tectonics of the Mid-Atlantic Ridge

near lat 37



N. Geological Society of America Bulletin, 88:541–555.

Macdonald, K.C., Miller, S.P., Luyendyk, B.P., Atwater, T.M., and

Shure, L., 1983. Investigation of a Vine-Matthews magnetic linea-

tion from a submersible: the source and character of marine mag-

netic anomalies. Journal of Geophysical Research, 88: 3403–3418.

Raff, A.D., and Mason, R.G., 1961. A magnetic survey off the west

coast of North America, 40-N to 52-N. Geological Society of

America Bulletin, 72: 1267–1270.

Rumbaugh, L.H., and Alldredge, L.R., 1949. Airborne equipment for

geomagnetic measurements. Transactions of American Geophysi-

cal Union, 30: 836–848.

Sheriff, R.E., 1981. Encyclopedic Dictionary of Exploration Geophysics,

6th edn. Tulsa, OK: Society of Exploration Geophysicists, 266 pp.

Tivey, M.A., Bradley, A., Yoerger, D., Catanach, R., Duester, A.,

Liberatore, S., and Singh, H., 1997. Autonomous underwater

vehicle maps seafloor. EOS, 78: 229–230.

Tivey, M.A., Schouten, H., and Kleinrock, M.C., 2003. A near-bottom

magnetic survey of the Mid-Atlantic Ridge axis at 26



N: Implica-

tions for the tectonic evolution of the TAG segment. Journal of

Geophysical Research, 108: 2277, 10.1029/2002JB001967.

Tivey, M.A., and Tucholke, B.E., 1998. Magnetization of O-29 Ma

ocean crust on the Mid-Atlantic Ridge, 25



to 27



N. Journal

of Geophysical Research, 103: 17807–17826.

Cross-references

Carnegie Institution of Washington,Department of Terrestrial Magnetism

Carnegie, Research Vessel

Geomagnetism, History of

Halley, Edmond (1656–1742)

IGRF, International Geomagnetic Reference Field

Instrumentation, History of

Observatories, Instrumentation

Project MAGNET

Reduction to Pole

Vine-Matthews-Morley Hypothesis

Voyages Making Geomagnetic Measurements

MAGNETIC SUSCEPTIBILITY, ANISOTROPY

Introduction

The preferred orientation of minerals is typical of almost all rock

types. In some rocks, for example, metamorphic mica-schist, it is very

strong and visible to the naked eye, while in others, like basalt and

massive granite, it is very weak and detectable only by sensitive instru-

ments. It develops during various geological processes, such as by

water flow in sediments, by lava or magma flow in volcanic and

plutonic rocks, or by ductile deformation in metamorphic rocks, and

in turn, these processes can be assessed from it. The preferred orienta-

tion of rock-forming minerals has been measured in thin sections using

microscope and universal stage analysis since the beginning of the

20th century, while today, more sophisticated techniques have been

developed (e.g., X-ray pole figure goniometry, neutron pole figure

goniometry, and electron backscatter diffractography).

Magnetic minerals, mostly occurring in rocks in accessory amounts,

show preferred orientation. This orientation, called magnetic fabric, can

be advantageously investigated by means of magnetic anisotropy, a

technique based on the directional variability in magnetic properties.

For example, the magnetic susceptibility of hematite or pyrrhotite crys-

tal is an order of magnitude higher within the basal plane than along

the c-axis, thus constituting the magnetocrystalline anisotropy. In mag-

netite grains, the susceptibility is the highest along the longest dimen-

sion of the grain, and lowest along the shortest dimension regardless of

the orientation of crystal lattice. This anisotropy is called shape aniso-

tropy. If the magnetic grains are oriented preferentially in a rock, the

rock shows magnetic anisotropy. Modern instruments are sensitive

enough to be able to measure anisotropy in almost all rock types with

sufficient accuracy. In addition, this technique is so sensitive that in

rocks with a very weak-preferred orientation of minerals (e.g., some

volcanic rocks), it is the only method that gives reasonable results.

This technique is also extremely fast, an order of magnitude faster than

classical methods of structural analysis. For these reasons, anisotropy

has experienced broad use in many branches of geology and geophy-

sics and has become one of the most important techniques of modern

structural geology.

Principles of anisotropy of magnetic susceptibility

The magnetization (M) of a magnetically isotropic substance is depen-

dent on the intensity of the magnetizing field (H) as follows:

M ¼ kH

where k is the magnetic susceptibility, independent of the field in para-

magnetic and diamagnetic substances and being a complex function of

the field in ferromagnetic sensu lato (in a broad sense) substances. In

weak fields, in which the so-called initial susceptibility is measured,

the susceptibility is also constant in ferromagnetic sensu lato substances.

If in magnetically anisotropic rocks, the magnetization is no longer

parallel to the magnetizing field, then, the relationship between the

magnetization and the intensity of the weak field is described in a

more complex way by a set of three equations:

¼ k

þ k

¼ k

þ k

¼ k

þ k

where M

(i ¼ 1, 2, 3) are the components of the magnetization vector,

( j ¼ 1, 2, 3) are the components of the vector of the intensity of

magnetic field, and k

¼ k

) are the components of the symmetric

second-rank susceptibility tensor that reflects the directional variation

of susceptibility in its shape. The susceptibility is the highest in one

direction and the lowest in a perpendicular direction. In these two

546 MAGNETIC SUSCEPTIBILITY, ANISOTROPY

directions and in a direction perpendicular to them, the magnetization

is parallel to the field. In the Cartesian coordinate system defined by

these directions, the above equations simplify to:

¼ k

The components k

 k

, often denoted as k

 k

,or

max

 k

int

 k

min

, are called the principal susceptibilities (the maxi-

mum, intermediate, and minimum susceptibilities) and their directions

are the principal directions. The susceptibility tensor, even though math-

ematically rigorous, is simple and elegant and is nonillustrative from a

geological point of view. Fortunately, it can be geometrically repre-

sented by the susceptibility ellipsoid or AMS ellipsoid (for details see

Nye, 1957) that are quite illustrative and frequently used in geological

interpretations of AMS; their definitions are clear from Figure M69.

The axes of the AMS ellipsoid are parallel to the principal directions

and the semiaxes lengths equal the principal susceptibilities.

AMS can be measured with various instruments (e.g., low-field torque

meter, AC induction bridge, anisotropy spinner magnetometer), their prin-

ciples being described in another entry of this volume. Nevertheless, the

principle of the AMS determination lies in measuring the susceptibility

of a specimen in at least six independent directions, and subsequently fit-

ting the susceptibility tensor to these data using the least-squares method

(Figure M70). Measuring susceptibility in more than six directions

enables the error in fitting the tensor as well as the errors in determining

the principal susceptibilities and principal directions to be evaluated.

For each principal direction, two error angles are determined that delimit

a region within which the true principal direction lies with a probability

of 95% (Figure M71; for details see Jelínek, 1977).

The theory of AMS in rocks works with field-independent suscept-

ibility that results from the linear relationship between magnetiza-

tion and the magnetizing field. This is valid in diamagnetic and

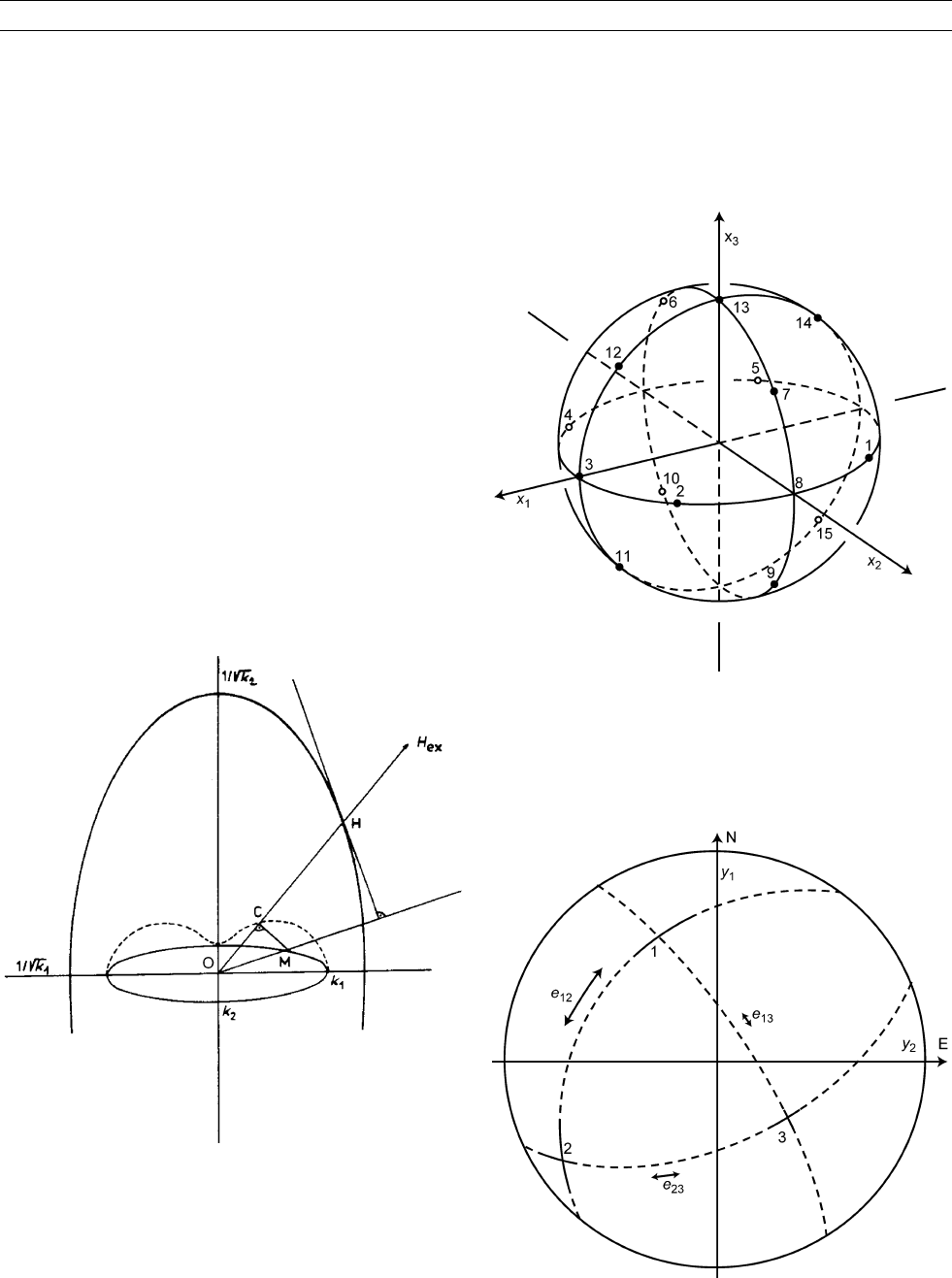
Figure M69 Definition of the susceptibility ellipsoid and AMS

ellipsoid. Legend: OH, direction of external magnetic field H

;

OM, anisotropic magnetization induced by H

; OC, component

of magnetization parallel to H

or the quantity measured by usual

methods. If \vert H

\vert ¼ 1, OC is the susceptibility parallel

to H

(directional susceptibility). Loci of H, where OH ¼ 1/

ﬃﬃﬃﬃﬃﬃﬃﬃ

represents the susceptibility ellipsoid (heavy line) and the loci of

M (thin line) is the AMS ellipsoid. The dashed line represents the

directional behavior of the directional susceptibility; note that it is

not represented by an ellipsoid. (Adapted from Nagata, 1961.)

Figure M70 Rotatable design (independent of the coordinate

system) of measuring directions used in the Jelı

nek (1977) method

for the AMS determination. Besides, some instruments measure a

slowly rotating specimen; consequently, a much larger set of

directional data is obtained. (After Jelı

nek, 1977.)

Figure M71 Confidence angles (e

, e

) that define the

regions where the true principal directions lie with probability of

95%. Specimen of granodiorite. (After Jelı

nek, 1977.)

MAGNETIC SUSCEPTIBILITY, ANISOTROPY 547

paramagnetic minerals by definition, as well as in ferromagnetic

minerals sensu lato, provided that the fields used in common AMS

meters are weak enough so that the initial susceptibility is measured.

Recently it has been shown that this is true for magnetite, while the

susceptibility of pyrrhotite, hematite, and titanomagnetite may be

field-dependent. This may theoretically result in the invalidity of the

AMS theory in rocks whose AMS is carried by these minerals. Fortu-

nately, the recent investigations have also shown that this effect does

not manifest in the orientations of the principal susceptibilities and

the AMS ellipsoid shapes. It affects only the degree of AMS, that

can be corrected by relatively simple means (de Wall, 2000; Hrouda,

2002). Consequently, the simple and elegant linear AMS theory may

be still in use.

The causes of the magnetic anisotropy of rocks are usually summarized

as follows: (1) the alignment of nonequidimensional grains, (2) the lattice

alignment of crystals with magnetocrystalline anisotropy, (3) the align-

ment of magnetic domains, (4) the stringing together of magnetic grains

(this is special case of (1)), (5) stress-induced anisotropy, and (6) exchange

anisotropy (Banerjee and Stacey, 1967). Extensive investigations of

magnetic anisotropy have shown that the dominant factors are (1) and

(2) (Tarling and Hrouda, 1993).

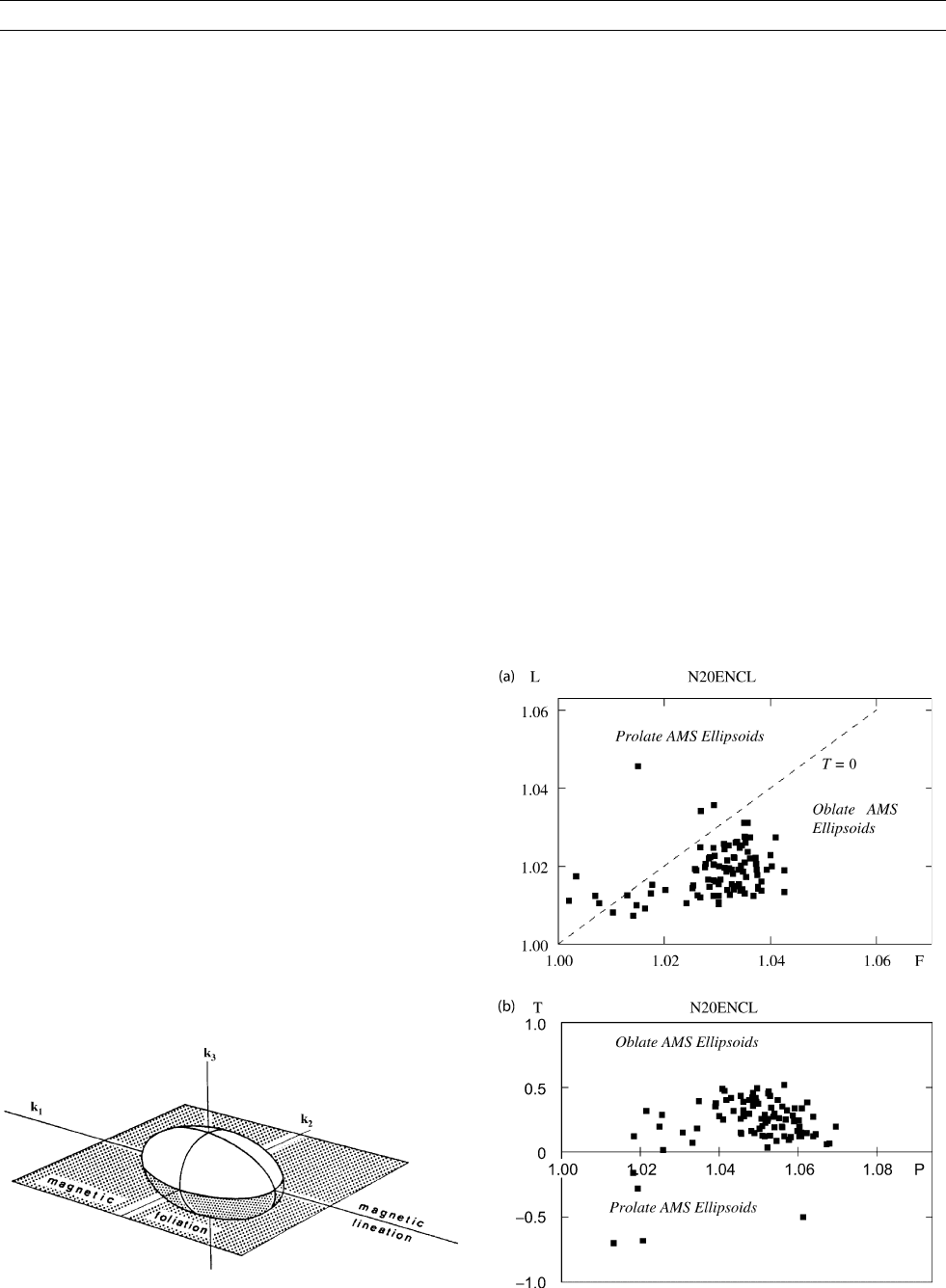
The eccentricity and shape of the AMS ellipsoid can be character-

ized by parameters derived from the relationship between the principal

susceptibilities. More than 30 such parameters have been introduced

(see Tarling and Hrouda, 1993), despite two are sufficient to do so.

The most commonly used are:

P ¼ k

—degree of AMS

¼ exp√{2[(

–)

þ (

–)

þ (

–)

]}—corrected degree

of AMS

L ¼ k

—magnetic lineation

F ¼ k

—magnetic foliation

T ¼ (2

–



)/(

–

)—shape parameter

q ¼ (k

– k

)/[(k

þ k

)/2 – k

]—shape parameter

where 

¼ lnk

, 

¼ lnk

, 

¼ lnk

,  ¼ (

þ 

)/3. The

parameters P and P

, being interrelated as P

¼ P

(a ¼ √T

/3), indicate

the intensity of the preferred orientation of the magnetic minerals in a

rock. The parameters L and F characterize the intensity of the linear-

parallel and planar-parallel orientations, respectively. The direction of

magnetic lineation is parallel to the maximum susceptibility, while

the magnetic foliation pole is parallel to the minimum susceptibility

(Figure M72). The parameters T and q characterize the shape of the

AMS ellipsoid. If 0 < T < þ1or0< q < 0.7 the AMS ellipsoid

is oblate (the magnetic fabric is planar); T ¼þ1orq ¼ 0 means

that the AMS ellipsoid is rotationally oblate. If 1 < T < 0or

0.7 < q < 2 the AMS ellipsoid is prolate (the magnetic fabric is

linear); T ¼1orq ¼ 2 means that the AMS ellipsoid is rotationally

prolate.

The eccentricity and shape of the AMS ellipsoid can be represented

graphically using two types of AMS plots (Figure M73a,b). In the first

type (Figure M73a), the magnetic foliation (F) is plotted on the

abscissa and the magnetic lineation (L ) on the ordinate, analogous to

the Flinn plot used by structural geologists. In the second type of plot

(Figure M73b), the degree of AMS (P or P

) is as abscissa and the T

parameter is the ordinate. The first plot type is convenient for the

AMS of deformed rocks because it formally resembles the deformation

plot used by structural geologists. The second plot type is convenient

in cases when the degree of AMS is of primary interest.

The orientations of the directions of the principal susceptibilities are

usually presented on the lower hemisphere of an equal-area projection.

The general convention is to use square symbols for k

, triangles for

, and circles for k

AMS of minerals

Whereas in paleomagnetism only ferromagnetic minerals sensu lato

are important, most frequently represented by magnetite, hematite,

and pyrrhotite, since they carry a remanent magnetization, in the

AMS are important not only these minerals, but also some paramag-

netic ferromagnesian silicates, as for example olivine, pyroxene,

augite, hornblende, mica, and diamagnetic calcite. The AMS of these

minerals are presented in Table M5, in terms of the degree of AMS,

the shape parameter, and the AMS type. The AMS of hematite and

pyrrhotite is magnetocrystalline in origin and extremely strong. In

ferromagnesian silicates and in calcite, the AMS is also magnetocrys-

talline but much weaker.

Figure M72 Definition of magnetic foliation and magnetic

lineation with respect to the AMS ellipsoid. (Adapted from

Siegesmund et al., 1995.)

Figure M73 Magnetic anisotropy plots. (a) L-F (Flinn type) plot

and (b) P-T (Jelı

nek type) plot.

548 MAGNETIC SUSCEPTIBILITY, ANISOTROPY

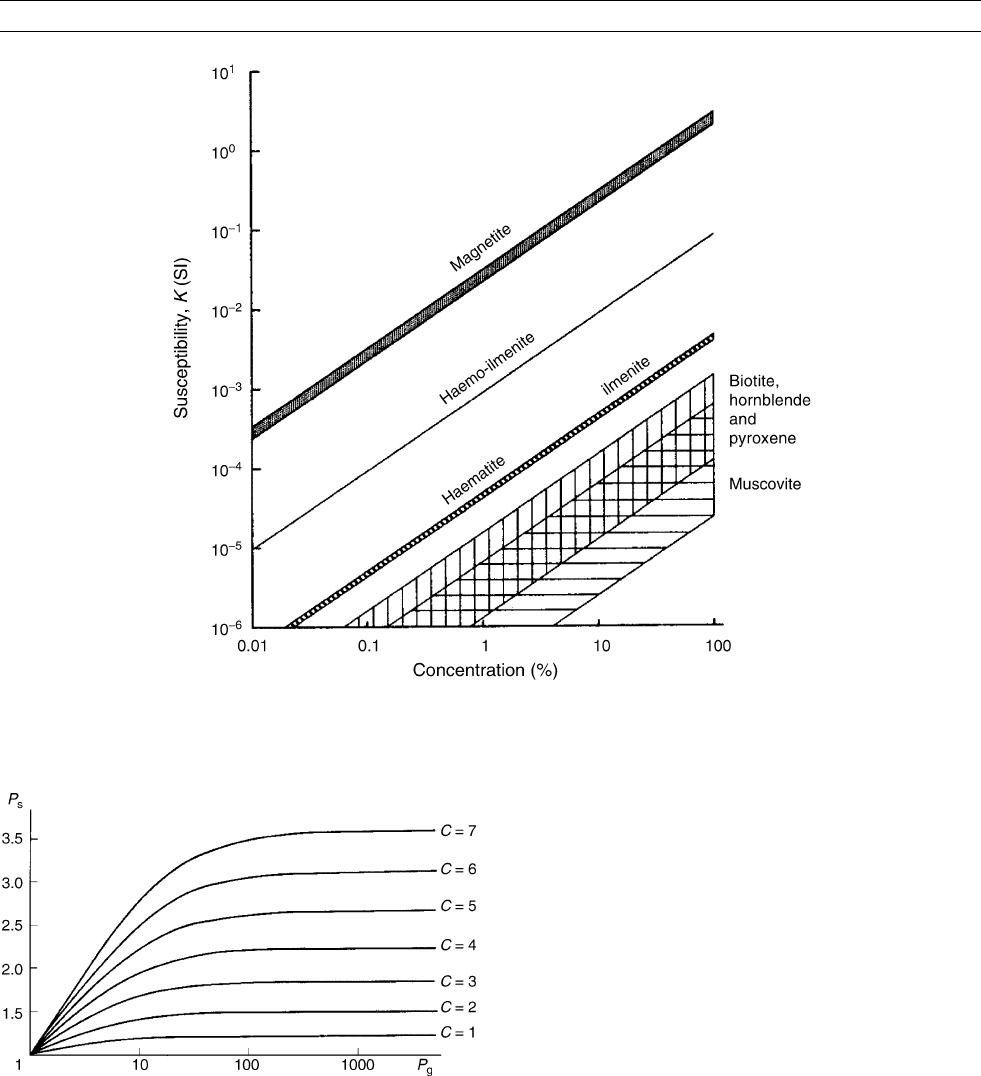
Magnetite displays shape anisotropy depending on the eccentricities

of the grains and on the intrinsic susceptibility of the mineral. The

degree of grain AMS is then (Uyeda et al ., 1963)

P ¼ð1 þ kN

Þ=ð1 þ kN

Þ;

where k is the intrinsic susceptibility, which is isotropic and dependent

only on the chemical composition of the mineral, and N

and N

which

are the demagnetizing factors along the longest and shortest grain

axes, respectively, solely depending on the grain shape. The quantitative

relationship, though straightforward, is relatively complex, described by

formulas containing elliptic integrals. Figure M74 shows this relation-

ship quantitatively. It is obvious that grains with a lower intrinsic sus-

ceptibility show a lower degree of AMS than the grains with a higher

intrinsic susceptibility having exactly the same shapes. Consequently,

the AMS data for magnetite presented in Table M5 are only informative.

Rock susceptibility, in general, is controlled by all minerals present

in a rock. Figure M75 shows model contributions of individual mineral

groups. In strongly magnetic rocks, with a bulk susceptibility higher

than 5  10

–3

(SI units), the effect of mafic silicates is negligible and

the rock susceptibility is effectively controlled by magnetite only.

In weakly magnetic rocks, with bulk susceptibility less than 5  10

–4

(SI units), the content of ferromagnetic minerals is often so low that

the susceptibility is effectively controlled by mafic silicates. In rocks

with a bulk susceptibility between 5  10

–4

and 5  10

–3

(SI units), the

AMS, in general, is controlled by both ferromagnetic and paramagnetic

minerals. If the bulk susceptibility is less than 5  10

–5

(SI units), neither

the effect of diamagnetic fraction (the calcite in marble) is negligible.

Quantitative relationship between AMS and mineral

preferred orientation

The AMS of rocks is controlled not only by the intensity of the pre-

ferred orientation of magnetic minerals, but also by their grain AMS.

The effect of these factors is obvious from a simple model in which

the degree of AMS of the rock (P

) is plotted against the degree of

AMS of the magnetic grains (P

) for different intensities of the preferred

orientation of the principal axes (characterized by parameter C in

Figure M76). If the grain anisotropy is small (similar to that of magne-

tite and phyllosilicates), the rock AMS is controlled by both the grain

AMS and the intensity of the preferred orientation. If the grain AMS

is high (as in hematite and pyrrhotite), the rock AMS is controlled solely

by the intensity of the preferred orientation of the magnetic axes.

The preferred orientation of minerals in rocks is traditionally repre-

sented by density diagrams presented on equal-area projections. The

density that maps the preferred orientation of a specific crystal axis

can be described mathematically by the orientation tensor, defined as:

E ¼



where l

, m

, n

are the direction cosines of the ith linear element repre-

sented by unit vector and N is the number of the linear elements con-

sidered (Scheidegger, 1965). The principal values of this tensor (E



 E

) have the following property:

þ E

¼ 1.

Consequently, E

> E

¼ E

represents a cluster type of distribution,

whereas E

¼ E

> E

corresponds to a girdle-type pattern

(Figure M77). In a perfect cluster, in which all linear elements are par-

allel, E

¼ 1, E

¼ 0, E

¼ 0. In a perfect girdle, E

¼ 0.5, E

¼ 0.5,

¼ 0.

A straightforward relationship exists between the orientation tensor

and the susceptibility tensor (for a summary see Ježek and Hrouda,

2000). For a rock, whose AMS is carried by a single magnetic mineral,

the relationship is:

k ¼ KI þ DE

where k is the rock susceptibility tensor, I is the identity matrix. For

magnetically rotational oblate grains, K ¼ K

¼ K

, D ¼ K

–K (K

, K

are the grain principal susceptibilities) and E is the orientation

tensor of the grain minimum susceptibility axes. For magnetically rota-

tional oblate grains, K ¼ K

¼ K

, D ¼ K–K

, and E is the orientation

tensor of the grain maximum susceptibility axes. For the grains dis-

playing so-called perfectly triaxial AMS (K

–K

¼ K

–K

), K ¼ K

D ¼ K

–K

¼ K

–K

and E ¼ E

–E

is the Lisle orientation tensor,

where E

and E

are the Scheidegger orientation tensors of the maxi-

mum and minimum axes, respectively.

Since the rock susceptibility is affected by all minerals present in the

rock, the theoretical rock susceptibility can be calculated if the sus-

ceptibility tensors of all minerals and their relative contributions are

known. Unfortunately, this is never known in practice and studies of

the quantitative relationship between the AMS and preferred orienta-

tion are made only in such rocks in which the contribution of one

mineral to the rock susceptibility is dominant. In this case, the model

rock susceptibility is:

Table M5 Grain AMS of various minerals (adapted from Hrouda

(1993)

Mineral PTAMS type

Magnetite 1.1–3.0 Variable Shape

Hematite >100 1 Magnetocrystalline

Pyrrhotite 100–10000 1 Magnetocrystalline

Actinolite 1.1–1.2 0.4–0.4 Magnetocrystalline

Hornblende 1.665 0.51 Magnetocrystalline

Crocidolite 1.098 0.25 Magnetocrystalline

Glaucophane 1.205 0.10 Magnetocrystalline

Chlorite 1.2–1.7 1 Magnetocrystalline

Biotite 1.2–1.6 1 Magnetocrystalline

Phlogopite 1.3 0.95 Magnetocrystalline

Muscovite 1.4 0.44 Magnetocrystalline

Quartz 1.01 – Magnetocrystalline

Calcite 1.11 1 Magnetocrystalline

Aragonite 1.15 0.80 Magnetocrystalline

Figure M74 Relation between the degree of grain AMS (P

) and

the dimension ratio a/b of prolate spheroid (titano-)magnetite

grains for various values of intrinsic susceptibility (SI). (Adapted

from Hrouda and Tarling, 1993.)

MAGNETIC SUSCEPTIBILITY, ANISOTROPY 549

k ¼ pSK ¼ pSðOK

Þ;

where k is the rock susceptibility tensor, K is the magnetic grain sus-

ceptibility tensor, K

the diagonal from the grain susceptibility tensor,

O the matrix specifying the mineral orientation (O

is the transposed

matrix of O), and p the percentage of a magnetic mineral in a rock.

The orientation of magnetic minerals can be investigated either

through direct measurement of individual grains (microscope and

universal stage methods), through determining the orientation tensor

using X-ray pole figure goniometry, or electron backscatter diffraction

with orientation contrast. Studies of this type were made for hematite

(deformed hematite ore, Minas Gerais, Brazil, Hrouda et al., 1985),

biotite (Bíteš orthogneiss, Hrouda and Schulmann, 1990), chlorites

(Lüneburg et al., 1999; Chadima et al., 2004), and calcite (Carrara

marble, Owens and Rutter, 1978). Results from these studies show that

the principal susceptibilities of the whole rock measured are oriented

in the same way as those calculated from the crystallographic axis pat-

tern. The degree of AMS and the shape parameter are not always in

agreement with that calculated from the crystallographic axis pattern.

The differences may reflect the situation that the AMS and X-ray mea-

surements are often not executed on exactly the same specimens, and

the respective specimen volumes differ substantially (1 cm

vs thin

section). In addition, minor effect of other magnetic minerals cannot

be excluded. Nevertheless, the agreement between the theoretical and

measured AMS can be considered to be satisfactory. Some of these

results are illustrated in Figure M78.

Resolution of AMS into paramagnetic and

ferromagnetic components

In rocks with the bulk susceptibility between 5  10

–4

and 5  10

–3

the AMS is, in general, controlled by both ferromagnetic and paramag-

netic minerals. As these mineral groups may behave differently in var-

ious geological situations, it is desirable to resolve the rock AMS into

its ferromagnetic and paramagnetic components. This resolution is

usually made through measuring the AMS in various strong magnetic

fields of the order of tesla in which the ferromagnetic and paramag-

netic minerals behave in a different way (described in an another part

Figure M75 Mineral contribution to the susceptibility of a rock. Note that 1% of magnetite contributes more than 100% of phyllosilicates.

(Adapted from Hrouda and Kahan, 1991.)

Figure M76 The dependence of the degree of AMS of a model

rock (P

) on the grain degree of AMS (P

) and on the parameter C

characterizing the intensity of the preferred orientation of the axes

of magnetically uniaxial grains. (Adapted from Hrouda, 1980.)

550 MAGNETIC SUSCEPTIBILITY, ANISOTROPY

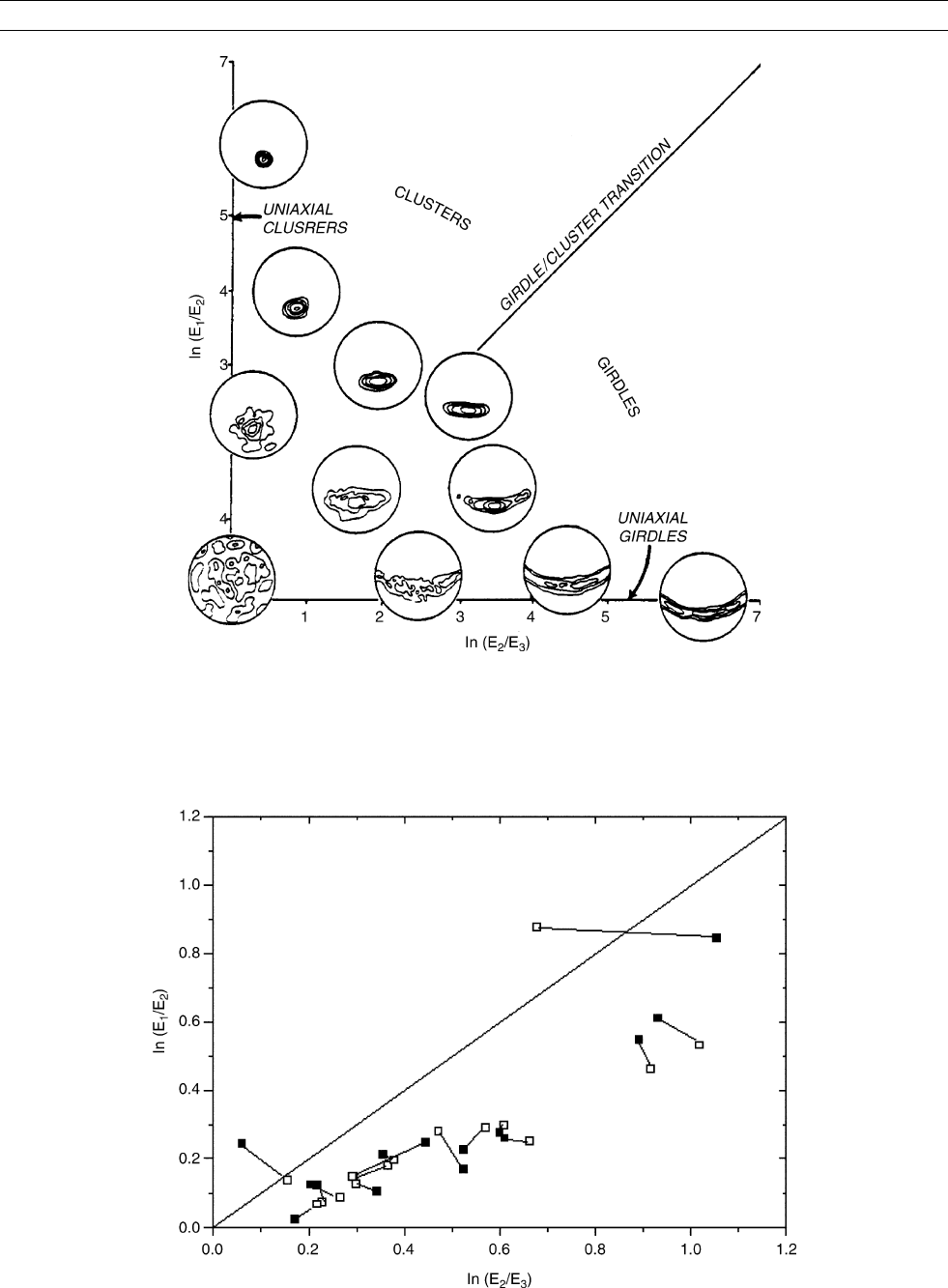
Figure M77 Relationship between preferred orientation of a linear element and principal values of the orientation tensor. (Adapted

from Woodcock, 1977.)

Figure M78 Relationship between orientation tensor calculated from mineral preferred orientation (c-axes of chlorite) and from AMS.

Constructed from Chadima et al. (2004) data.

MAGNETIC SUSCEPTIBILITY, ANISOTROPY 551

of this volume) or at variable temperatures in which the ferromagnetic

and paramagnetic minerals also behave differently.

Variation of the susceptibility of paramagnetic minerals with tempera-

ture is represented by a hyperbola, while in ferromagnetic minerals it is

a complex curve in case of magnetite characterized by acute susceptibil-

ity decreases at about 155



C, the Verwey transition, and at about

580



C, the Curie temperature. Fortunately, in some temperature inter-

vals, typically between room temperature and 200



C, the ferromagnetic

susceptibility is either constant or follows only a mildly sloped straight

line (Figure M79).

The susceptibility vs temperature curve of a rock containing both

ferromagnetic and paramagnetic minerals for the case in which the fer-

romagnetic susceptibility is constant within the considered temperature

interval, is:

k ¼ p

C=T þ p

;

and for the case in which the ferromagnetic susceptibility is repre-

sented by only a mildly sloped straight line, it is:

k ¼ p

C=T þ p

ðbT þ aÞ;

where k is the rock susceptibility, k

the ferromagnetic susceptibility,

and p

the percentages of paramagnetic and ferromagnetic fractions,

respectively, C the paramagnetic constant and T the absolute tempera-

ture, a and b are constants.

The first equation is that of a hyperbola offset along the susceptibil-

ity axis, and the second is a combination of a hyperbola and a straight

line. By fitting the hyperbola and straight line either horizontal (first

equation), or sloped (second equation) to k vs T curve using the

least-squares method, one obtains the paramagnetic susceptibility con-

tribution ( p

C/T ) and the ferromagnetic susceptibility contribution ( p

or p

(bT þ a)). These methods were developed by Hrouda (1994)

and Hrouda et al. (1997), respectively, and are broadly used in resol-

ving the mean bulk susceptibility measured on powder specimens into

paramagnetic and ferromagnetic components.

Richter and van der Pluijm (1994) developed a technique for the

AMS resolution into the paramagnetic and ferromagne tic components

based on susceptibility measurements at low temperatures (between

the temperature of liquid nitrogen and room temperature). At these

temperatures, the contribution of paramagnetic fraction to the rock sus-

ceptibility is amplified because of the hyperbolic course. By plotting the

reciprocal susceptibility against temperature one can easily visualize

the linear paramagnetic susceptibility contribution and separate it from

the ferromagnetic contribution. If this measurement is made in six direc-

tions, one can obtains six directional paramagnetic and ferromagnetic

susceptibilities from which the paramagnetic and ferromagnetic suscept-

ibility tensor can be calculated in a standard way (Figure M80).

Thermal enhancement of the magnetic fabric

The AMS is often measured using the instrumentation of a paleomag-

netic laboratory. Paleomagnetic techniques, such as AF demagnetiza-

tion and thermal demagnetization, have then been logically tested as

to whether they are also applicable to the AMS (Urrutia-Fucugauchi,

1981). It has been shown that the AF demagnetization has only weak

effect on the AMS and its use ceased. On the other hand, the effect of

thermal demagnetization on the AMS can be strong. However, thermal

demagnetization mechanisms are different in AMS than in remanent

magnetization. Thermal demagnetization affects the induced magneti-

zation very weakly, probably negligibly, but may induce the creation

of new magnetic phases or even new minerals. If this creation is made

in a zero magnetic field, it would have virtually no effect on the rema-

nent magnetization, but would have a very strong effect on the AMS.

Often, the newly created phases are more magnetic than the original

phases and may be coaxial to the old phases. Thermal demagnetiza-

tion, in fact, enhances the original magnetic fabric. Newly created

phases can also be noncoaxial, and their creation may obscure the ori-

ginal magnetic fabric. If the new creation is confined to a phase of dif-

ferent origin than the original phase, thermal treatment may “visualize”

the cryptic fabric (Henry et al., 2003). Even though positive results

may be obtained in this way in some cases, this technique cannot be

recommended to be used in a routine way because the process of

the creation of new magnetic phases due to specimen heating is very

complex, and our knowledge about this is far from complete.

Statistical evaluation of the AMS data

The AMS technique is so fast that several specimens are usually mea-

sured in a site. The site data or the data from geological bodies should

be evaluated statistically. The simplest approach is to consider the indi-

vidual principal directions as vectors and to process them using a vec-

tor statistics, for example the Fisher statistics. Unfortunately, the

principal directions do not have a Fisherian distribution, being ortho-

gonal and bipolar, so various modifications of the Fisher statistics have

been proposed (Ellwood and Whitney, 1980; Park et al., 1988).

To avoid these problems Jelínek (1978) has developed a statistical

method that is based on averaging out the individual components of

the susceptibility tensors in one coordinate system (e.g., geographical)

after they have been normalized against their mean susceptibility.

In this way the mean tensor (and the orientations of its principal

directions) as well as the elliptical confidence regions (in terms of con-

fidence angles) about each principal direction are computed from the

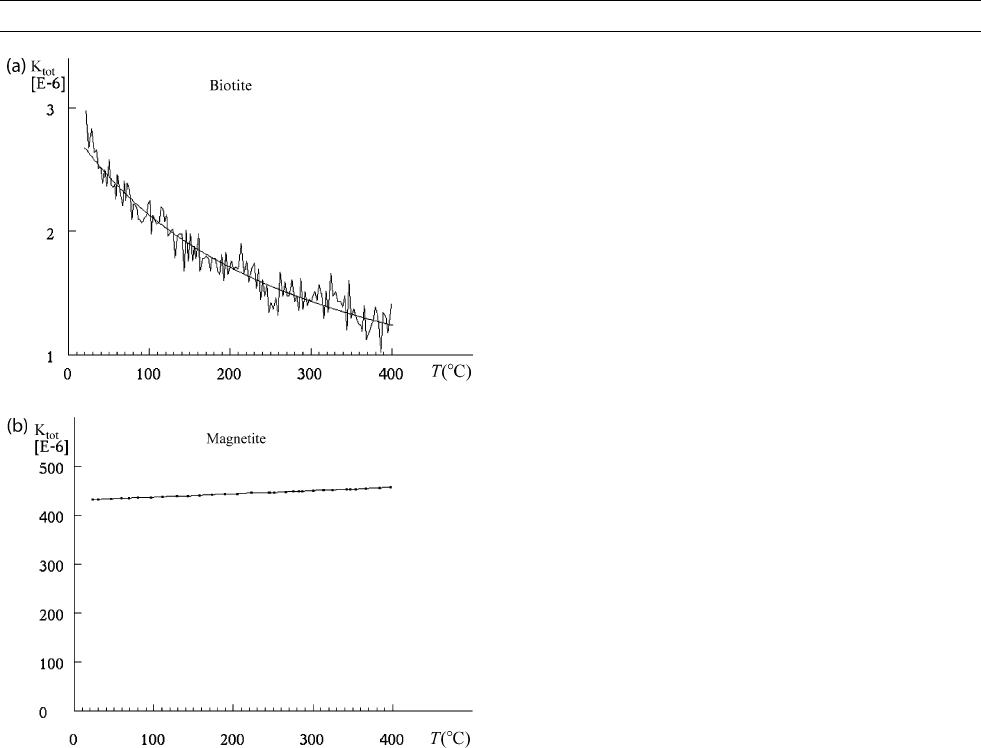
Figure M79 Susceptibility vs temperature relationship in the

temperature interval between room temperature and 200

C for

biotite (a) and magnetite (b).

552 MAGNETIC SUSCEPTIBILITY, ANISOTROPY

variance-covariance matrix (Figure M81). This technique seems to be

the most frequently used at present.

In data sets with widely scattered principal directions, neither ana-

lytical method provides an adequate visual representation of the

observed data. To overcome these disadvantages, Constable and Tauxe

(1990) developed a bootstrap method which delineates the confidence

regions using Monte Carlo probability modeling.

Statistical evaluation of the AMS data is a complex problem and

further investigations are required to evaluate the effectiveness of the

individual methods (for discussion see Ernst and Pearce, 1989; Tarling

and Hrouda, 1993; Borradaile, 2001).

Geological applications of AMS

Magnetic fabric in sedimentary rocks

The AMS in sedimentary rocks provides information on the deposition

and compaction processes (for a summary, see Hamilton and Rees,

1970; Rees and Woodall, 1975; Rees, 1983; Taira, 1989; Tarling and

Hrouda, 1993; Hrouda and Ježek, 1999). In natural sedimentary rocks

unaffected by later deformation, the relationship that is primarily inves-

tigated is the agreement between the magnetic foliation and lineation and

the sedimentary external structures (sole markings, flute casts, groove

casts) and internal structures (cross-bedding, current-ripple lamination,

symmetric and asymmetric ripples). It has been found that the magnetic

foliation is always oriented near the bedding/compaction plane, while

the magnetic lineation is mostly roughly parallel to the near-bottom

water current directions determined using sedimentological techniques

(see Figure M82). Less frequently, the magnetic lineation may be per-

pendicular to the current direction, which is typical of the flysch sedi-

ments of the lowermost A member of the Bouma sequence. The degree

of AMS is relatively low and the AMS ellipsoid is, in general, oblate.

In artificial sediments deposited through grain by grain (or from

thin suspension) deposition from still or running water onto a flat or

sloping bottom under controlled conditions in tanks and flumes in

laboratories, the AMS ellipsoid is clearly oblate; the magnetic foliation

dips less than 15



from the bedding toward the origin of flow and the

magnetic lineation is parallel to the direction of flow, slightly plunging

toward the origin of flow.

During deposition from medium-concentrated suspensions, the

AMS ellipsoids can be clearly triaxial to slightly prolate, in which the

Figure M80 Principle of the resolution of AMS into paramagnetic and ferromagnetic components using measurement of

low-temperature susceptibility. (a) Six orientations of a specimen used to construct the susceptibility tensor, (b) the relative amount

of paramagnetic and ferromagnetic susceptibilities is determined in six orientations from heating curves, the upper curve being the

original heating curve and the lower curve being the paramagnetic remnant, and (c) the resolved paramagnetic and ferromagnetic

subtensors. (Adapted from Richter and van der Pluijm, 1994.)

Figure M81 Results of statistical evaluation of the AMS data from

a locality of the C

ista

granodiorite made by the Jelı

nek (1978)

method. Small symbols indicate individual specimens, and large

symbols indicate the mean tensor. The confidence regions around

the mean principal directions are elliptic on a sphere, being

slightly deformed due to the equal area projection.

MAGNETIC SUSCEPTIBILITY, ANISOTROPY 553

magnetic foliation dips less than 15



toward the origin of flow, and

the magnetic lineation is perpendicular to the direction of flow and to

the dip of magnetic foliation. During deposition from very concentrated

grain dispersions onto a sloping bottom, the AMS ellipsoids are triaxial.

The magnetic foliation dips 25



–30



toward the origin of the flow and

the magnetic lineation is parallel both to the flow and to the dip of

magnetic foliation, and plunges slightly toward the origin of flow.

During the process of diagenesis, the originally sedimentary mag-

netic fabric may be slightly modified due to ductile deformation

accompanying this process. If the ductile deformation is represented

by vertical shortening due to the loading by the weight of the overly-

ing strata, the degree of AMS and the oblateness of the AMS ellipsoid

increase, whereas the magnetic foliation and lineation retain their

orientations (e.g., Lowrie and Hirt, 1987). If the ductile deformation

is represented by the bedding parallel shortening or by the bedding

parallel simple shears or by both, the degree of AMS initially decreases

and only later increases when the deformation is strong enough to over-

come the initial compaction. The magnetic fabric initially becomes more

planar, and only later it does become more triaxial or even linear. The mag-

netic lineation deviates gradually from the direction of flow toward that of

maximum strain, often creating a bimodal pattern. The magnetic foliation

remains initially near the bedding. After a stronger strain, it deviates from

it, creating a girdle in the magnetic foliation poles that are perpendicular to

the magnetic lineation.

Magnetic fabric in volcani c rocks

The AMS of volcanic rocks is, in general, very weak, reflecting a very

poor dimensional orientation of the magnetic minerals (mostly titano-

magnetites) in these rocks. In spite of this, their AMS can, in general,

be measured precisely because the volcanic rocks are often strongly

magnetic, and the AMS seems to be the quickest method to be able

to reliably investigate the weakly preferred orientation of the minerals.

Since the first investigations of the AMS of volcanic rocks it has

been clear that it reflects the dimensional orientation of magnetic

minerals created during a lava flow. The magnetic foliation is often

found to be near or even parallel to the flow plane in lava flows, sills,

and dikes (Ernst and Baragar, 1992; Ca



non-Tapia et al., 1994; Raposo

and Ernesto, 1995; Hrouda et al., 2002a). The magnetic lineation is

mostly parallel to the lava flow directions (Figure M83), even though

perpendicular or oblique relationships can also be rarely found.

AMS enables not only the lava flow process to be investigated, but

also the rheomorphic flow in ignimbrites and the motions of tuffs and

tuffites (MacDonald and Palmer, 1990).

Magnetic fabric in plutonic rocks

In plutonic rocks, the AMS is one of the most powerful tools of struc-

tural analysis, because it can efficiently measure the magnetic fabric

even in massive granites that are isotropic at the first sight. The AMS

of plutonic rocks varies from very weak (typical of volcanic rocks)

to extraordinarily strong (typical of metamorphic and/or strongly

deformed rocks).

Granites, the most important representatives of plutonic rocks,

usually display a bimodal distribution of their magnetic susceptibility.

One mode corresponds to susceptibilities in the order of 10

–5

to 10

–4

SI units and are due to weakly magnetic (Dortman, 1984) or paramag-

netic (Bouchez, 2000) granites. These are equated with the S (sedimental)

type granites, such as the ilmenite-bearing granites. The other mode

has susceptibilities in the order of 10

–3

–10

–2

SI units, and this is

due to magnetic or ferromagnetic granites. These are equated with

the I (igneous) type granites such as magnetite-bearing granites. In

magnetic granites, the AMS investigates the preferred orientation of

magnetite by grain shape. In weakly magnetic granites, the AMS

reflects the preferred orientation of mafic silicates (mainly biotite,

and less frequently amphibole) by crystal lattice.

The plutonic rocks that have suffered no postintrusive deformation

show the magnetic fabric created during the process of magma empla-

cement. The characteristic features of this magnetic fabric are as

follows: the degree of AMS is relatively low, indicating only weak

preferred orientation of magnetic minerals created during the liquid

flow of magma; the magnetic fabric ranges from oblate to prolate

according to the local character of the magma flow; the magnetic folia-

tion is parallel to the flow plane and the magnetic lineation is parallel

to the flow direction; the magnetic foliations are steep in stocks and

upright sheetlike bodies in which the magma flowed vertically

(Figure M84). On the other hand, it is oblique or horizontal in the bodies

where the magma could not ascend vertically and moved in a more

complex way. The magnetic lineation can be vertical, horizontal, or obli-

que according to the local direction of the magma flow. The magnetic

fabric elements usually show a close relationship to the shapes of mag-

matic bodies and to magmatic structural elements, if observable. Many

examples are shown in the book by Bouchez et al. (1997).

Some plutonic rocks exhibit a very high degree of AMS and a very

high mean magnetic susceptibility. The magnetic fabric in these rocks

usually indicates a preferred orientation of magnetite by grain shape

that is younger than the fabric of the surrounding silicates and takes

its shape from highly anisometric intergranular (interfoliation) spaces.

This magnetic fabric is usually termed as the mimetic magnetic fabric

(e.g., Hrouda et al., 1971).

Some granites have suffered tectonic ductile deformation after their

emplacement. In this process, the originally intrusive magnetic fabric

is overprinted or even obliterated by the deformational magnetic fab-

ric. The degree of AMS of such rocks is often much higher, because

the ductile deformation is a relatively efficient mechanism for the reor-

ientation of magnetic minerals. The magnetic foliations and lineations

deviate from the directions of the intrusive fabric elements toward the

directions of the principal strains. A good example includes granites of

the West Carpathians whose magnetic fabrics are coaxial with those of

surrounding metamorphic rocks and covering sedimentary rocks as

result of ductile deformation associated with retrogressive deformation

acting during creation and motion of the West Carpathian nappes

(Hrouda et al., 2002b).

Figure M82 Magnetic and sedimentary fabrics in sediments of the

Rosario Formation, La Jolla, California (crosses, magnetic foliation

poles; open circles, magnetic lineation). Equal-area projection on

lower hemisphere (projection plane ¼ bedding plane). (Adapted

from von Rad, 1971.)

554 MAGNETIC SUSCEPTIBILITY, ANISOTROPY

AMS of metamorphic and deformed rocks

The AMS of metamorphic rocks in general and even of low-grade

metamorphic rocks is considerably higher than the AMS in unde-

formed sedimentary and volcanic rocks. Hence, the mechanism orient-

ing magnetic grains during low-grade metamorphism is very effective.

It probably involves ductile deformation or recrystallization in an

anisotropic stress field operating during metamorphism. The AMS

therefore enables these processes to be studied.

AMS is an extremely powerful tool in investigating the progressive

modification of the sedimentary magnetic fabric by ductile deformation

that takes place in accretionary prisms (Figure M85). After sediment

deposition, the AMS ellipsoid is usually oblate with the magnetic folia-

tion near the bedding, and if a magnetic lineation is present, it is near

the current direction. In initial stages of deformation, represented by

shortening along the bedding, the AMS ellipsoid changes from oblate

to triaxial; the degree of AMS may slightly decrease, the magnetic folia-

tion remains parallel to bedding, but the magnetic lineation reorients

perpendicular to the shortening direction. In progressing deformation,

spaced cleavage develops and the magnetic lineation becomes parallel

to the bedding/cleavage intersection line. The AMS ellipsoid becomes

prolate. If the deformation continues, giving rise to the development of

slaty cleavage, the AMS ellipsoid becomes oblate again, the degree of

AMS considerably increases, the magnetic foliation pole reorientates

parallel to the cleavage and the magnetic lineation remains parallel to

the bedding/cleavage intersection line. If the deformation is very strong,

the magnetic lineation may be dip-parallel in the cleavage plane.

AMS can be used in revealing the origin of folds (Hrouda, 1978;

Hrouda et al., 2000). Various types of folds differing in terms of the

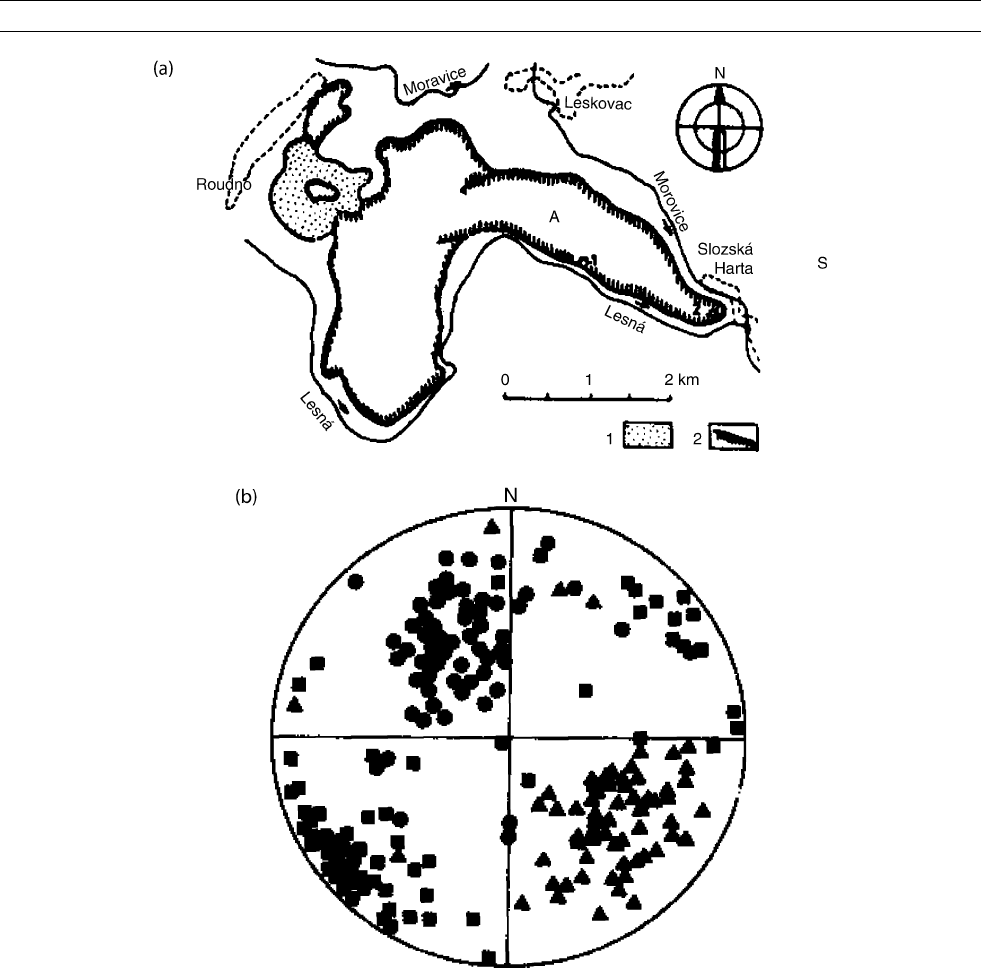
Figure M83 Magnetic fabric in basalt of the Chr

ibsky

les lava flow. (a) Synoptic geological map of the Chr

ibsky

les lava flow (A) and its

environs (Legend: 1, basalt tuff; 2, boundaries of lava bodies), (b) orientations of principal susceptibilities in the quarry 1 (Legend:

triangle, magnetic lineation; square, intermediate susceptibility; circle, magnetic foliation pole). Equal-area projection on lower

hemisphere. (Adapted from Kolofı

kova, 1976.)

MAGNETIC SUSCEPTIBILITY, ANISOTROPY 555