Harris C.M., Piersol A.G. Harris Shock and vibration handbook
Подождите немного. Документ загружается.


The next step is to find the kinetic and potential energies of the wave motion of
the plate. The kinetic energy may be determined from the transverse velocity of the
plate at each point over the circle of radius a covered by the wave. Figure 9.2 shows
an approximate distribution of velocity over the circle of radius a at the end of
impact.
8
The direction of the impact also is shown. The kinetic energy in the wave at
the end of impact is
T =
a
0
1
⁄2 ⋅ 2h ⋅ ρ
1
⋅ 2πR ⋅ ˙w
2
dR (9.9)
where ˙w is the transverse velocity at distance R from the origin. As an approxima-
tion it is assumed that the sum of the potential energy and the kinetic energy in the
wave is 2T. With considerable effort
these energies can be calculated in terms
of the motion of the plate, although the
calculation may be laborious.
The impulse in the plate produced by
the colliding body is
J =
a
0
1
⁄2 ⋅ 2h ⋅ ρ
1
⋅ 2πR ⋅ ˙w dr (9.10)
The integration should be carried out
with due regard to the sign of velocity. If
m
u
is the mass of colliding body, ˙u its
velocity before impact, and e the coeffi-
cient of restitution, the following rela-
tions are obtained on the assumption
that the energy is conserved:
1
⁄2 m
u
˙u
2
(1 − e
2
) = 2T (9.11)
m
u
˙u(1 + e) = J (9.12)
Equation (9.11) represents the energy lost to the moving sphere as a result of impact
and Eq. (9.12) represents the change in momentum of the sphere.
The coefficient of restitution e is determined by evaluating the integrals for T and
J and substituting their values in Eq. (9.12). The necessary integrations can be per-
formed by taking the function for transverse velocity in Fig. 9.2 as arcs of sine curves.
The resultant expression for e is
e = (9.13)
where a, the radius of the deformed region, is given by Eq. (9.8) and τ
H
, the time of
contact between sphere and plate, is given by Hertz’s theory of impact to a first
approximation.
4
The mass of the sphere is m
u
; the mass of the plate is assumed to be
infinite. Large discrepancies between theory and experiment occur when the diam-
eter of the sphere is large compared with the thickness of the plate. The duration of
impact τ
H
is
hρ
1
a
2
− 0.56m
u
hρ
1
a
2
+ 0.56m
u
9.4 CHAPTER NINE
FIGURE 9.2 Distribution of transverse veloc-
ities in plate as a result of impact by a moving
body. (After Lamb
8
.)
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.4

τ
H
= 2.94
where α=
ν
1
2
+
m
u
2/5
R
s
−1/5
(9.14)
The radius of the striking sphere is R
s
and its velocity before impact is ˙u. Subscripts
1 and 2 represent the properties of the sphere and plate, respectively. The value of τ
H
may be substituted in Eq. (9.8) above.
Experimental results verify the theory when the limitations of the theory are not
violated. The velocity of impact must be sufficiently small to avoid plastic deforma-
tion.When the collision involves steel on steel, the velocity usually must be less than
1 ft/sec. However, useful engineering results can be obtained with this approach
even though plastic deformation does occur locally.
9, 10
TRANSVERSE IMPACT OF A MASS ON A BEAM
If F(t) is the force acting between the sphere and the beam during contact, the dis-
tance traveled by the sphere in time t after collision is
11
˙ut −
t
0
F(t
v
) (t − t
v
) dt
v
(9.15)
where ˙u = velocity of sphere before collision (beam assumed to be at rest initially)
m
u
= mass of solid sphere
The beam is assumed to be at rest initially.
For example, the deflection of a simply supported beam under force F(t
v
) at its
center is
∞
1,3,5...
t
0
F(t
v
) dt
v
(9.16)
where m
b
= one-half of mass of beam
ω
n
= angular frequency of the nth mode of vibration
Equation (9.16) represents the transverse vibration of a beam. While the present case
is only for direct central impact, the cases for noncentral impact depend only on the
corresponding solution for transverse vibration. Oblique impact also is treated readily.
The expression for the relative approach of the sphere and beam, i.e., penetration
of beam by sphere, is
11
α=κ
1
F(t)
2⁄3
(9.17)
where κ
1
is a constant depending on the elastic and geometrical properties of the
sphere and the beam at the point of contact, and α is given by Eq. (9.14). Conse-
quently, the equation that defines the problem is
α=K
1
F
2/3
= ˙ut −
t
0
F(t
v
)(t − t
v
) dt
v
−
∞
1,3,5
t
0
F(t
v
) dt
v
(9.18)
sin ω
n
(t − t
v
)
ω
n
1
m
b
1
m
u
sin ω
n
(t − t
v
)
ω
n
1
m
b
1
m
u
1 −ν
2
2
E
2
1 −ν
1
2
E
1
15
16
α
˙u
EFFECTS OF IMPACT ON STRUCTURES 9.5
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.5

Equation (9.18) has been solved numerically for two specific problems by subdi-
viding the time interval 0 to t into small elements and calculating, step by step, the
displacements of the sphere.
11
The results are not general but rather apply only to
the cases of beam and sphere.
For the impact of a mass on a beam, the sum of the kinetic and the potential ener-
gies may be expressed in terms of the unknown contact force.
12
Also, the impulse
integral J in terms of the contact force may be expressed as
J =
t
0
F(t) dt = m
u
˙u(1 + e) (9.19)
A satisfactory approximation to F(t) is defined in terms of a normalized force
F:
F(t) = m
u
˙u(1 + e)
F(t) (9.20)
Thus, from Eqs. (9.19) and (9.20),
t
0
Fdt= 1 (9.21)
The value of this integral is independent of the shape of F(t). The normalized force
is defined such that its maximum value equals the maximum value of the correspon-
ding normalized Hertz force.
12
To perform the necessary integrations, a suitable
function for defining F(t) is chosen as follows:
F(t) = sin t [0 < t <τ
L
]
F(t) = 0[|t| >τ
L
]
(9.22)
Results for particular problems solved in this manner agree well with those obtained
for the same problems by the numerical solution of the exact integral equation.
12
To apply these results to a specific beam impact problem, it is necessary to
express the deflection equation for the beam in terms of known quantities. One of
these quantities is the coefficient of restitution; a formula must be provided for its
determination in terms of known functions. This is given by Eq. (9.31).
IMPACT OF A RIGID BODY ON A DAMPED
ELASTICALLY SUPPORTED BEAM
For the more general case of impact of a rigid body on a damped, elastically sup-
ported beam, it is assumed that there is external damping, damping determined by
the Stokes’ law of stress-strain, and an elastic support attached to the beam along its
length in such a manner that resistance is proportional to deflection.
13
The differen-
tial equation for the deflection of the beam is
EI + c
1
I + c
2
+ kw +ρS = F(x,t) (9.23)
where w = deflection, in.
E = Young’s modulus, lb/in.
2
I = moment of inertia for cross section (constant), in.
4
∂
2
w
∂t
2
∂w
∂t
∂
5
w
∂x
4
∂t
∂
4
w
∂x
4
π
τ
L
π
2τ
L
9.6 CHAPTER NINE
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.6

c
1
= internal damping coefficient, lb/in.
2
-sec (Stokes’ law)
c
2
= external damping coefficient, lb/in.
2
-sec
k = foundation modulus, lb/in.
2
ρ= density, lb-sec
2
/in.
4
S = area of cross section (constant), in.
2
= acceleration, in./sec
2
t = time, sec
F(x,t) = driving force per unit length of beam, lb/in.
For example, to illustrate the application of specific boundary conditions, con-
sider a simply supported beam of length l. The moments and deflections must van-
ish at the ends. The beam is assumed undeflected and at rest just before impact, and
central impact is assumed although with some additional computation this restric-
tion may be dropped. The solution may be written as follows:
w(x,t) =
∞
sin sin
×
t
0
e−δ
n
(t −τ)
sin
ω
n
2
−
δ
n
2
⋅ (t −τ)
F
1
(τ) dτ
(9.24)
where e = base of natural logarithms
δ
n
= damping numbers =
r
i
+ r
e
r
i
=
r
e
=
ω
n
= angular frequencies
m =
1
⁄2ρAl
A satisfactory analytical expression for the contact force F
1
(t), a particularization
of F(x,t) in Eq. (9.23), must be developed. Although F
1
(t) is assumed to act at the
center of the beam, the methods apply with only minor alterations if the impact
occurs at any other point of the beam.
One of the conditions which the contact force must satisfy is that its time integral
for the duration of impact equal the change in momentum of the striking body. The
change of momentum is
m˙z − m˙z′=m˙z
1 −
(9.25)
where m = mass of rigid body, lb-sec
2
/in.
˙z = velocity of rigid body just before collision, in./sec
˙z′=velocity of rigid body just after collision, in./sec
When the velocity of the beam is zero, Eq. (9.1) may be written
˙z′
˙z
c
2
ρS
c
1
I
ρS
n
4
π
4
l
4
1
2
1
ω
n
2
−
δ
n
2
1
m
nπ
2
nπx
l
∂
2
w
∂t
2
EFFECTS OF IMPACT ON STRUCTURES 9.7
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.7

e =− (9.26)
Equation (9.26) may be written
m˙z
1 −
= m˙z(1 + e) (9.27)
From the equivalence of impulse and momentum:
τ
0
0
F
1
(t) dt = m˙z(1 + e) (9.28)
where τ
0
is the time of contact.
It can then be shown
13
that the impact force may be written
F
1
(t) = m˙z(1 + e) sin [0 < t <τ
L
]
F
1
= 0[t >τ
L
]
(9.29)
It can be shown further
13
that
τ
L
= 3.28
⋅
1⁄5
(9.30)
where R = radius of sphere, in.
ν= Poisson’s ratio
The time interval τ
L
is a special value of the time of contact T
0
. It agrees well with
experimental results.
The coefficient of restitution e is
13
e =
1 −
∞
1
Φ
n
−
∞
1
Ψ
n
(9.31)
1 +
∞
1
Φ
n
+
∞
1
Ψ
n
where m = mass of sphere
m
b
= half mass of beam
The functions Φ
n
and Ψ
n
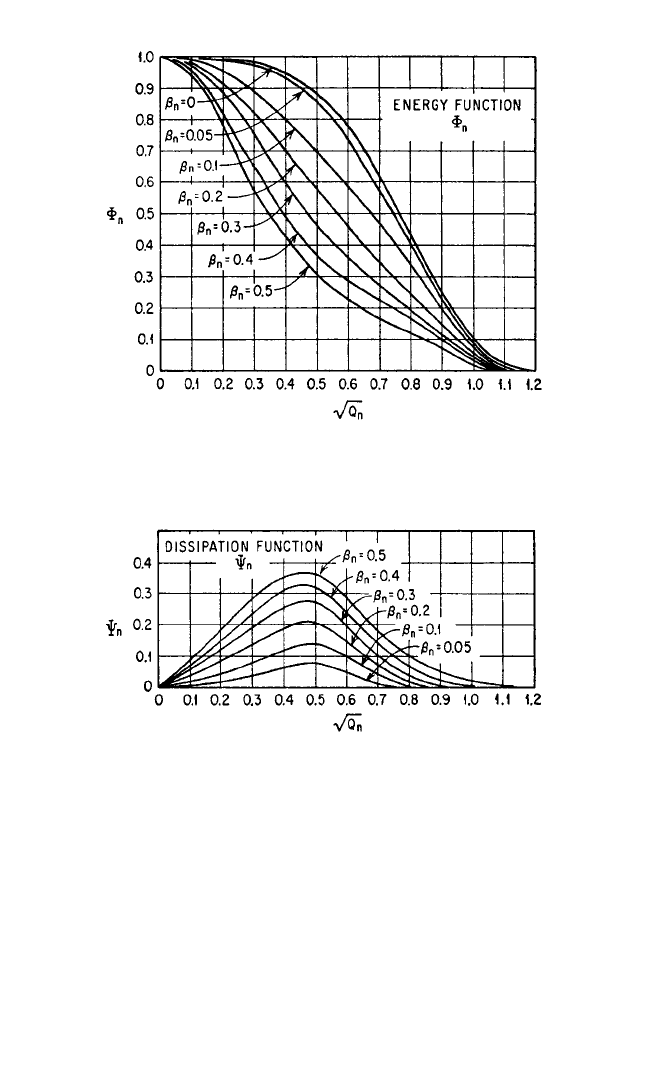
are given in the form of curves in Figs. 9.3 and 9.4; the sym-
bol β
n
=δ
n
/ω
n
represents fractional damping and Q
n
=ω
n
τ
L
/2π is a dimensionless fre-
quency where ω
n
= angular frequency of nth mode of vibration of undamped vibration
of beam, rad/sec, and τ
L
= length of time the sinusoidal pulse is assumed to act on
beam [see Eq. (9.30)]. If damping is neglected, the functions Ψ
n
vanish from Eq. (9.31).
The above theory may be generalized to apply to the response of plates to
impact. The deflection equation of a plate subjected to a force applied at a point is
required. The various energy distributions at the end of impact are arrived at in a
manner analogous to that for the beam.
The theory has been applied to columns and continuous beams
14, 15
and also could
be applied to transverse impact on a ring. Measurement of the force of impact illus-
trates the large number of modes of vibration that can be excited by an impact.
16, 17, 22
m
m
b
m
m
b
m
m
b
m
m
b
(1 −ν
2
)
E
2
m
2
˙zR
nπt
τ
L
π
2τ
L
˙z′
˙z
˙z′
˙z
9.8 CHAPTER NINE
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.8
Principal qualitative results of the foregoing analysis are:
1. Impacts by bodies of relatively small mass moving with low velocities develop
significant bending strains in beams.
2. External damping of the type assumed above has a rapidly decreasing effect on
reducing deflection and strain as the number of the mode increases.
3. Internal damping of the viscous type here assumed reduces deflection and strain
appreciably in the higher modes. For a sufficiently high mode number, the vibra-
tion becomes aperiodic.
4. Increasing the modulus for an elastic foundation reduces the energy absorbed by
the structure from the colliding body.
EFFECTS OF IMPACT ON STRUCTURES 9.9
FIGURE 9.3 Energy functions Φ
n
used with Eq. (9.31) to deter-
mine the coefficient of restitution from the impact of a rigid body
on a damped elastically supported beam.
FIGURE 9.4 Dissipative (damping) functions Ψ
n
used with Eq.
(9.31) to determine the coefficient of restitution from the impact of
a rigid body on a damped elastically supported beam.
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.9

5. Impacts from collision produce sharp initial rises in strain which are little influ-
enced by damping.
6. Because of result 5, the fatigue problem for machines and structures, in which the
impact conditions are repeated many times, can be serious. Ordinary damping
affords little protection.
7. The structure seldom can be treated as a single degree-of-freedom system with
any degree of reliability in predicting strain.
13, 19
LONGITUDINAL AND TORSIONAL
IMPACT ON BARS
If a mass strikes the end of a long bar, the response may be investigated by means of
the Hertz contact theory.
11
The normal modes of vibration must be known so the dis-
placement at each part of the bar can be calculated in terms of a contact force. In a
similar manner, the torsional vibration of a long bar can be studied, using the normal
modes of torsional vibration.
PLASTIC DEFORMATION RESULTING
FROM IMPACT
Many problems of interest involve plastic deformation rather than elastic deforma-
tion as considered in the preceding analyses. Using the concept of the plastic hinge,
the large plastic deformation of beams under transverse impact
23
and the plastic
deformation of free rings under concentrated dynamic loads
24
have been studied. In
such analyses, the elastic portion of the vibration usually is neglected. To make fur-
ther progress in analyses of large deformations as a result of impact, a realistic the-
ory of material behavior in the plastic phase is required.
An attempt to solve the problem for the longitudinal impact on bars has been
made using the static engineering-type stress-strain curve as a part of the analysis.
25
An extension of the work to transverse impact also was attempted.
26
Figure 9.5 illustrates the impact of a large body m colliding axially with a long
rod. The body m has an initial velocity ˙u and is sufficiently large that the end of the
rod may be assumed to move with constant velocity ˙u. At any time t a stress wave
will have moved into the bar a definite distance; by the condition of continuity (no
break in the material), the struck end of the bar will have moved a distance equal to
the total elongation of the end portion of the bar:
˙ut = ⋅ l (9.32)
The velocity c of a stress wave is c = l/t, and Eq. (9.32) becomes
= (9.33)
The stress and strain in an elastic material are related by Young’s modulus. Substi-
tuting for strain from Eq. (9.33),
˙u
c
9.10 CHAPTER NINE
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.10

σ= ⋅ E = E (9.34)
where ˙u = velocity of end of rod,
in./sec
l = distance stress wave trav-
els in time t, in.
t = time, sec
σ= stress, lb/in.
2
= strain (uniform), in./in.
E = Young’s modulus, lb/in.
2
c = velocity of stress wave
(dilatational), in./sec
When the yield point of the material is exceeded, Eq. (9.34) is inapplicable.
Extensions of the analysis, however, lead to some results in the case of plastic defor-
mation.
25
The differential equation for the elastic case is
E =ρ (9.35)
where u = displacement, in.
x = coordinate along rod, in.
t = time, sec
E = Young’s modulus, lb/in.
2
ρ = mass density, lb-sec
2
/in.
4
The velocity of the elastic dilatational wave obtained from Eq. (9.35) is
c =
The modulus E is the slope of the stress-strain curve in the initial linear elastic
region. Replacing E by ∂σ/∂ for the case in which plastic deformation occurs, the
slope of the static stress-stress curve can be determined at any value of the strain .
25
Equation (9.35) then becomes
=ρ (9.36)
Equation (9.36) is nonlinear; its general solution never has been obtained. For the
simple type of loading discussed above and an infinitely long bar, the theory predicts
a so-called critical velocity of impact because the velocities of the plastic waves are
much smaller than those for the elastic waves and approach zero as the strain is
indefinitely increased.
25
Since the impact velocity ˙u is an independent quantity, it can
be made larger and larger while the wave velocities are less than the velocity for
elastic waves. Hence a point must be reached at which the continuity of the material
is violated. Experimental data illustrate this point.
27
∂
2
u
∂t
2
∂
2
u
∂x
2
∂σ
∂
E
ρ
∂
2
u
∂t
2
∂
2
u
∂x
2
˙u
c
EFFECTS OF IMPACT ON STRUCTURES 9.11
FIGURE 9.5 Longitudinal impact of moving
body on end of rod.
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.11

ENERGY METHOD
Many problems in the design of machines and structures require knowledge of the
deformation of material in the plastic condition. In statical problems the method of
limit design
28
may be used. In dynamics, the most useful corresponding concept is
less theoretical and may be termed the energy method; it is based upon the impact
test used for the investigation of brittleness in metals. Originally, the only purpose of
this test was to break a standard specimen as an index of brittleness or ductility. The
general method, using a tension specimen, may be used in studying the dynamic
resistance of materials.
27
An axial force is applied along the length of the specimen
and causes the material to rupture ultimately. The energy of absorption is the total
amount of energy taken out of the loading system and transferred to the specimen
to cause the plastic deformation. The elastic energy and the specific mode of build-
up of stress to the final plastic state are ignored. Such an approach has value only to
the extent that the material has ductility. For example, in a long tension-type speci-
men of medium steel, the energy absorbed before neck-down and rupture is of the
order of 500 ft-lb per cubic inch of material. Thus, if the moving body in Fig. 9.5
weighs 200 lb and has an initial velocity of 80 ft/sec, it represents 20,000 ft-lb of
kinetic energy. If the tension bar subjected to the impact is 10 in. long and 0.5 in. in
diameter, it will absorb approximately 1,000 ft-lb of energy. Under these circum-
stances it will rupture. On the other hand, if the moving body m weighs only 50 lb
and has an initial velocity of 30 ft/sec, its kinetic energy is approximately 700 ft-lb
and the bar will not rupture.
If the tension specimen were severely notched at some point along its length, it
would no longer absorb 500 ft-lb per cubic inch to rupture.The material in the imme-
diate neighborhood of the notch would deform plastically; a break would occur at
the notch with the bulk of the material in the specimen stressed below the yield
stress for the material.A practical structural situation related to this problem occurs
when a butt weld is located at some point along an unnotched specimen. If the weld
is of good quality, the full energy absorption of the entire bar develops before rup-
ture; with a poor weld, the rupture occurs at the weld and practically no energy is
absorbed by the remainder of the material. This is an important consideration in
applying the energy method to design problems.
REFERENCES
1. Love, A. E. H.:“The Mathematical Theory of Elasticity,” p. 25, Cambridge University Press,
New York, 1934.
2. Timoshenko, S., and D. H.Young:“Engineering Mechanics,” McGraw-Hill Book Company,
Inc., New York, 1956.
3. Loney, S. L.: “A Treatise on Elementary Dynamics,” p. 199, Cambridge University Press,
New York, 1900.
4. Hertz, H.: J. Math. (Crelle), pp. 92, 155, 1881.
5. Rayleigh, Lord: Phil. Mag. (ser. 6), 11:283 (1906).
6. Timoshenko, S.: “Theory of Elasticity,” 3d ed., McGraw-Hill Book Company, Inc., New
York, 1969.
7. Raman, C. V.: Phys. Rev., 15, 277 (1920).
8. Lamb, H.: Proc. London Math. Soc., 35, 141 (1902).
9.12 CHAPTER NINE
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.12

9. Hoppmann, II, W. H.: Proc. SESA, 9:2, 21 (1952).
10. Hoppmann, II, W. H.: Proc. SESA, 10:1, 157 (1952).
11. Timoshenko, S.: “Vibration Problems in Engineering,” 3d ed., p. 413, D. Van Nostrand
Company, Inc., Princeton, N.J., 1955.
12. Zener, C., and H. Feshbach: Trans.ASME, 61:a-67 (1939).
13. Hoppmann, II, W. H.: J. Appl. Mechanics, 15:125 (1948).
14. Hoppmann, II, W. H.: J. Appl. Mechanics, 16:370 (1949).
15. Hoppmann, II, W. H.: J. Appl. Mechanics, 17:409 (1950).
16. Goldsmith, W., and D. M. Cunningham: Proc. SESA, 14:1, 179 (1956).
17. Barnhart, Jr., K. E., and Werner Goldsmith: J. Appl. Mechanics, 24:440 (1957).
18. Emschermann, H. H., and K. Ruhl: VDI-Forschungsheft 443, Ausgabe B, Band 20, 1954.
19. Hoppmann, II, W. H.: J. Appl. Mechanics, 19 (1952).
20. Wenk, E.,Jr.: Dissertation,The Johns Hopkins University, 1950, and David W.Taylor Model
Basin Rept. 704, July 1950.
21. Compendium, “Underwater Explosion,” O. N. R., Department of the Navy, 1950.
22. Prager,W.: James Clayton Lecture, The Institution of Mechanical Engineers, London, 1955.
23. Lee, E. H., and P. S. Symonds: J. Appl. Mechanics, 19:308 (1952).
24. Owens, R. H., and P. S. Symonds: J. Appl. Mechanics, 22 (1955).
25. Von Kármán, T.: NDRC Rept. A-29, 1943.
26. Duwez, P. E., D. S. Clark, and H. F. Bohnenblust: J. Appl. Mechanics, 17, 27 (1950).
27. Hoppmann, II, W. H.: Proc. ASTM, 47:533 (1947).
28. Symposium on the Plastic Theory of Structures, Cambridge University, September 1956,
British Welding J., 3(8) (1956); 4(1) (1957).
EFFECTS OF IMPACT ON STRUCTURES 9.13
8434_Harris_09_b.qxd 09/20/2001 11:19 AM Page 9.13
