Хисамутдинов И.А. (ред.) Основы экономики и теории рынка
Подождите немного. Документ загружается.

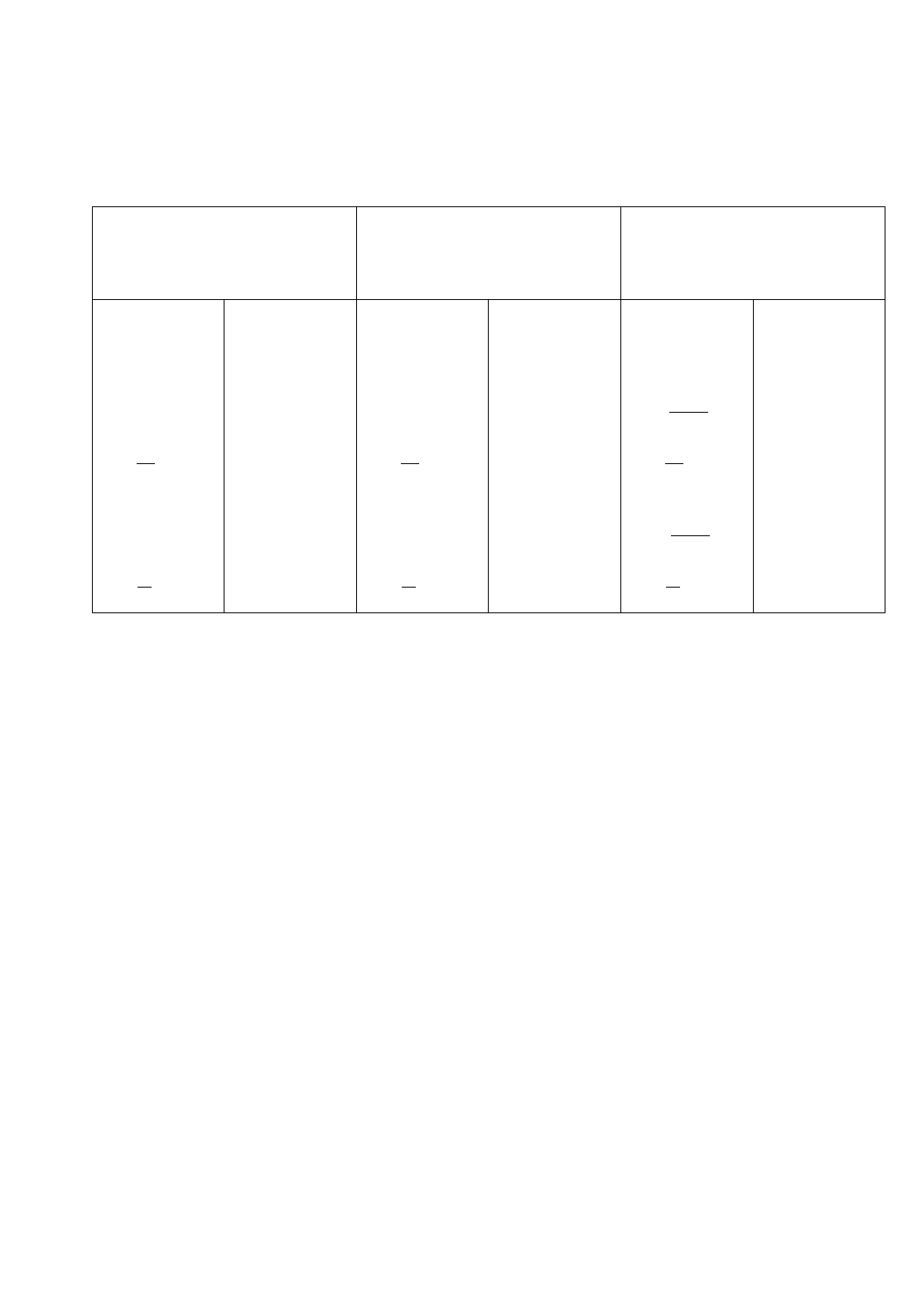
316
Таблица 12.1
Характеристика основных переменных модели Солоу
в состоянии устойчивого равновесия
При отсутствии роста
населения и
технологического
прогресса
При росте населения с
темпом п
При росте населения с
темпом п и
технологическом
прогрессе с темпом g
переменная
темп роста
переменная
темп роста
переменная
темп роста
L
0
L
n
L
n
L·E
n+g
K
0
K
n
K
n+g
EL
K
k
0
L
K
k
0
L
K
k
0
L
K
k
g
Y
0
Y
n
Y
n+g
EL
Y
y
0
L
Y
y
0
L
Y
y
0
L
Y
y
g
Таким образом, в модели Солоу найдено объяснение
механизма непрерывного экономического роста в режиме
равновесия при полной занятости ресурсов.
Как известно, в кейнсианских моделях норма сбережения
задавалось экзогенно и определяла величину равновесного темпа
роста дохода. В неоклассической модели Солоу при любой норме
сбережения рыночная экономика стремится к соответствующему
устойчивому уровню фондовооруженности (k*) и
сбалансированному росту, когда доход и капитал растут с темпом
(n+g). Величина нормы сбережения (накопления) является
объектом экономической политики и важна при оценке различных
программ экономического роста.
Поскольку равновесный экономический рост совместим с
различными нормами сбережения (как мы видели, увеличение
лишь на короткое время ускоряло рост экономики, в длительном
периоде экономика возвращалась к устойчивому равновесию и
постоянному темпу роста в зависимости от значения п и g),
возникает проблема выбора оптимальной нормы сбережения.
Оптимальная норма накопления, соответствующая “золотому
правилу” Э. Фелпса, обеспечивает равновесный экономический

317
рост с максимальным уровнем потребления. Устойчивый уровень
фондовооруженности соответствующий этой норме накопления,
обозначим k**, а потребления – с**.
Уровень потребления в расчете на одного занятого при любом
устойчивом значении фондовооруженности k* определяется путем
ряда преобразований исходного тождества: у=с+i. Выражаем
потребление с через у и i и подставляем значения данных
параметров, которые они принимают в устойчивом состоянии: с=у-
i, с*=ƒ(k*)-dk*, где с* — потребление в состоянии устойчивого
роста, а i=s·ƒ(k)=dk по определению устойчивого уровня
фондовооруженности. Теперь из различных устойчивых уровней
фондовооруженности (k*), соответствующих разными значениям s,
необходимо выбрать такой, при котором потребление достигает
максимума (рис. 12.6).
Рис. 12.6. «Золотое правило» Э. Фелпса
Если выбрано k*<k**, то объём выпуска увеличивается в
большей степени, чем величина выбытия (линия ƒ(k*) на графике
круче, чем dk*), а значит разница между ними, равная
потреблению, растет. При k*>k** увеличение объема выпуска
меньше роста выбытия, т.е. потребление падает. Рост потребления
возможен лишь до точки k**, где оно достигает максимума
(производственная функция и кривая dk* имеют здесь одинаковый
наклон). В этой точке увеличение запаса капитала на единицу даст
прирост выпуска, равный предельному продукту капитала (МРК), и
увеличит выбытие на величину d (износ на единицу капитала).
Роста потребления не будет, если весь прирост выпуска будет
использован на увеличение инвестиций для покрытия выбытия.
Таким образом, при уровне фондовооруженности,

318
соответствующем “золотому правилу” (k**), должно выполняться
условие: МРК=d (предельный продукт капитала равен норме
выбытия)
10
, а с учетом роста населения и технологического
прогресса: МРК=d+п+g.
Если экономика в исходном состоянии имеет запас капитала
больший, чем следует по “золотому правилу”, необходима
программа по снижению нормы накопления. Эта программа
обусловливает увеличение потребления и снижение инвестиций.
При этом экономика выходит из состояния равновесия и вновь
достигает его при пропорциях, соответствующих “золотому
правилу”.
Если экономика в исходном состоянии имеет запас капитала
меньше, чем k**, необходима программа, направленная на
повышение нормы сбережения. Эта программа первоначально
приводит к росту инвестиций и падению потребления, но по мере
накопления капитала с определенного момента потребление вновь
начинает расти. В результате экономика достигает нового
равновесия, но уже в соответствии с “золотым правилом”, где
потребление превышает исходный уровень. Данная программа
обычно считается непопулярной в связи с наличием “переходного
периода”, характеризующегося падением потребления, поэтому её
принятие зависит от межвременных предпочтений политиков, их
ориентации на краткосрочный или долгосрочный результат.
Рассмотренная модель Солоу позволяет описать механизм
долгосрочного экономического роста, сохраняющий равновесие в
экономике и полную занятость факторов. Она выделяет
технический прогресс как единственную основу устойчивого роста
благосостояния и позволяет найти оптимальный вариант роста,
обеспечивающий максимум потребления.
Представленная модель не свободна и от недостатков. Модель
анализирует состояния устойчивого равновесия, достигаемые в
длительной перспективе, тогда как для экономической политики
важна и краткосрочная динамика производства и уровня жизни.
Многие экзогенные переменные модели Солоу – s,d,n,g - было бы
предпочтительнее определять внутри модели, поскольку они тесно
связаны с другими её параметрами и могут видоизменять конечный
10
Этот же результат можно получить, учитывая тот факт, что функция потребления
достигает максимума при равенстве нулю её первой производной: (c*)´=[ƒ(k*)-dk*]´ = 0.

319
результат. Модель не включает также целый ряд ограничителей
роста, существенных в современных условиях — ресурсных,
экологических, социальных. Используемая в модели функция
Кобба-Дугласа, описывая лишь определенный тип взаимодействия
факторов производства, не всегда отражает реальную ситуацию в
экономике. Эти и другие недостатки пытаются преодолеть
современные теории экономического роста.
В неоклассической модели роста объём выпуска в устойчивом
состоянии растет с темпом (п+g), а выпуск на душу населения — с
темпом g, т.е. устойчивый темп роста определяется экзогенно.
Современные теории эндогенного роста пытаются определить
устойчивый темп роста в рамках модели, эндогенно, связывал его
со всеми возможными количественными и качественными
факторами: ресурсными, институциональными и др.
Сторонники концепции “экономики предложения” полагают,
что увеличение темпов роста при полной занятости возможно
прежде всего путём сокращения регулирующего вмешательства
извне в рыночную систему.
12.3. Экономический цикл: понятие, фазы, причины
колебаний
Теория экономических циклов изучает временную динамику
колебаний экономической активности, анализирует их причины и
объясняет механизмы их возникновения и развития.
Направления и характер изменения основных
макроэкономических показателей называются экономической
конъюнктурой. Поэтому теорию экономических циклов называют
также и теорией экономической конъюнктуры.
Основной вопрос, на который призвана ответить теория
экономических циклов, заключается в следующем: почему динамика
важнейших макроэкономических показателей, таких, как уровень
производства, занятости и т.д., подвержена циклическим
колебаниям? При этом, какие из всех возможных причин колебаний
основных макроэкономических параметров наилучшим образом
объясняют фактические колебания экономической активности?

320
Экономический цикл
11
можно определить как временной
интервал между двумя качественно одинаковыми состояниями
экономической конъюнктуры. Продолжительность цикла
определяется как период между двумя соседними высшими или
низшими поворотными точками ( ).
Рис. 12.7. Фаза экономического цикла
В модели цикла выделяют четыре фазы (рис.12.7):
- первая фаза – бум (II), при котором экономика достигает
максимальной активности. Это период сверхзанятости (экономика
находится выше уровня потенциального объема производства,
выше тренда) и инфляции. Экономика в этом состоянии называется
«перегретой»;
- вторая фаза – спад (III) – деловая активность начинает
сокращаться, фактический ВВП доходит до своего потенциального
уровня и продолжает падать ниже тренда, что приводит экономику
к следующей фазе – кризису;
- третья фаза – кризис (IV), или стагнация, экономика
находится в состоянии рецессионного разрыва, поскольку
фактический ВВП меньше потенциального. Это период
недоиспользования экономических ресурсов, т.е. высокой
безработицы;
- четвертая фаза – оживление (I), или подъем, экономика
постепенно начинает выходить из кризиса, фактический ВВП
приближается к своему потенциальному уровню, а затем
11
Термины «экономический цикл», «бизнес-цикл», «деловой цикл, «цикл экономической
конъюнктуры» являются синонимами.
I
I
II
III
I
IV
I
I
II
t
1
t
2
y
t

321
превосходит его, пока не достигнет своего максимума, что вновь
приведет к фазе бума.
Для характеристики состояния и динамики экономической
конъюнктуры используются различные показатели, важнейшими из
которых являются объем ВНП, уровень занятости, уровень загрузки
производственных мощностей, объем прибыли предпринимателей и
другие параметры. При этом, в зависимости от того, как
макроэкономические параметры меняются в ходе экономического
цикла, их можно разделить на проциклические, контрциклические и
ациклические.
Проциклические переменные имеют тенденцию к росту в
период подъема и к снижению в период спада.
Контрциклические переменные имеют тенденцию к снижению
в период подъема и к росту в период спада.
Ациклическими называются переменные, динамика которых не
связана непосредственно с циклами деловой активности.
Темпы динамики различных параметров, как правило, не
совпадают: в то время как одни из проциклических переменных еще
возрастают, другие уже снижаются, соответственно, в то время как
одни из контрциклических переменных еще снижаются, другие уже
возрастают. Этим, в частности, объясняется, что смена фаз подъема и
спада происходит достаточно плавно.
Поэтому экономические переменные различают в зависимости
от того, достигают ли они максимума (минимума) до или после
достижения экономикой высшей (низшей) поворотной точки
экономического цикла. Выделяют три типа макроэкономических
параметров: опережающие, запаздывающие и соответствующие.
Опережающими, или ведущими (leading), считаются такие
параметры, которые достигают максимума (минимума) перед
достижением пика (дна) экономической активности.
Запаздывающими (lagging) считаются такие параметры,
которые достигают максимума (минимума) после достижением пика
(дна) экономической активности.
Соответствующими (coincident) считаются такие параметры,
которые меняются одновременно с динамикой экономической
активности.

322
12.4. Виды и теории экономических циклов
Выделяют различные виды циклов по продолжительности:
- столетние циклы, длящиеся 100 лет и более;
- длинные или циклы Кондратьева, продолжительность которых
составляет 40- 60 лет и которые названы в честь выдающегося
русского экономиста Николая Дмитриевича Кондратьева,
разработавшего теорию «длинных волн экономической
конъюнктуры». Кондратьев предположил, что наиболее
разрушительные кризисы происходят, когда совпадают точки
максимума спада деловой активности длинноволнового цикла и
классического. Примерами таких кризисов могут служить кризис
1873 г., великая депрессия 1929 – 1933 гг., стагфляция 1974 – 1975 гг.
«Длинные волны» не являются колебаниями: кризисы в «большой
волне» не обязательно отражают абсолютное падение производства.
Это изменение темпов роста вокруг долговременных тенденций.
Фазы «длинных волн»: восстановление, длинный подъем, большой
кризис. Смена одной «длинной волны» другой – это переход от
одного технологического способа производства к другому,
включающий качественные в рабочей силе и системе образования,
коренные новации в организационно-экономических отношениях
волны» другой – это переход от одного технологического способа
производства к другому, включающий качественные в рабочей силе
и системе образования, коренные новации в организационно-
экономических отношениях, структурную революция в сфере
управления. Циклы Кондратьева связаны с открытиями или с
важными техническими нововведениями и их распространением.
- средние или классические циклы (деловые или бизнес-циклы).
Первый «классический» кризис (кризис перепроизводства)
произошел в Англии в 1825г., а с 1857г. такие кризисы стали
мировыми. В период до Второй мировой войны продолжительность
этих циклов составляла 10-12 лет, а в настоящее время - 5-8 лет.
Наиболее точно деловые циклы – колебания инвестиционных
расходов, ВВП, инфляции и безработицы – описывает модель
циклических колебаний Жюгляра;
- циклы С. Кузнеца занимают промежуточное положение между
«длинными волнами» и среднесрочными циклами. Они связаны с
долгосрочным накоплением факторов производства и имеют период
15 – 23 года.

323
- короткие или циклы Китчина продолжительностью 2 - 4 года –
состоят в нарушениях и восстановлениях равновесия рыночных
спроса и предложения на потребительские товары. Отклонения от
него могут быть краткосрочными и длительными. Краткосрочные
отклонения устраняются моментально: или поступлением товара со
склада в торговлю, или задействованием резервных мощностей
производства. Длительные отклонения преодолеваются в течение 3 –
4 лет путем перепрофилирования производства на выпуск
пользующихся повышенным спросом потребительских благ или
создания дополнительных производственных мощностей для их
выпуска. Каждый цикл завершается новым равновесием при уже
измененных пропорциях в спросе на потребительские товары. Циклы
Китчина связаны с движением запасов, изменениями в банковском
клиринге и оптовых ценах.
Все вышеназванные циклы связаны с инвестициями и
опираются на три лаговых процесса: цикл Китчина связан с разрывом
во времени между выделением инвестиций и вводом новых средств
труда; цикл Жугляра – с разрывом во времени между вводом и
выбытием активной части средств труда; циклы Кузнеца (в
основном) и Кондратьева связаны с разрывом во времени между
вводом и выбытием пассивной части средств труда. При этом цикл
Китчина зависит от динамики чистых инвестиций, а циклы Жугляра,
Кузнеца и Кондратьева – от валовых инвестиций, связанных с
обновлением капитала.
Реальное воспроизводство оказывается совмещением,
сплетением и взаимоналожением разных циклов. Совмещенные
циклы образуют тот экономический цикл, с которым повседневно
имеют дело все субъекты экономики.
Следует сразу отметить, что какой-либо единой теории
экономического цикла к настоящему времени не создано. Более
того, существует достаточно большой разброс во взглядах на причины
возникновения и механизмы деловых циклов. К тому же практические
исследования подтверждают, что колебания экономической
активности в разных странах достаточно сильно различаются по
регулярности, длительности и причинам возникновения.
Поэтому современная теория циклов представляет собой
определенную совокупность различных моделей, с некоторыми
упрощениями формализующих процесс экономической динамики,
наиболее известные из которых представлены ниже. Тем не менее,

324
исходя из результатов имеющихся исследований можно попытаться
(хотя и с некоторой долей условности) делать некоторые
обобщения.
Первая серьезная попытка обобщения в теории экономических
циклов была предпринята Артуром Бернсом и Уэсли Клэр Митчеллом
в их исследовании, являвшимся частью широкомасштабного проекта,
проводимого в течение нескольких десятилетий Национальным бюро
экономических исследований (США).
Одна из основных гипотез, лежащих в основе подхода Бернса и
Митчелла, состоит в том, что динамику рядов выпуска и занятости
обуславливая экономический рост, известный как возрастающий
тренд, а цикл деловой активности представляет собой колебания
вокруг тренда (рис. 12.8).
Тренд есть результат действия факторов, обуславливающих
долговременный рост в экономике: уровня сбережений, прироста
труда и капитала, технологических сдвигов и т.п. Факторы же,
определяющие вид делового цикла, практически не влияют на
формирование долговременного тренда. То бизнес-цикл представляет
собой временные отклонения от долгосрочного тренда.
Рис. 12.8. Гипотетическая модель делового цикла А.Бернса и
У.Митчелла
Долгое время данная гипотеза являлась общепринятой, однако в
некоторых недавних исследованиях обоснованность различий между
трендом и циклом поставлена под сомнение. Некоторые авторы
высказывают точку зрения, что существенная часть колебаний
выпуска происходит вследствие постоянных шоков, а не временных
отклонений от неизменного тренда. По их мнению, последствия
случайных воздействий на выпуск достаточно устойчивы во
времени. Например, если выпуск неожиданно резко возрастет в

325
текущем периоде, то и тренд в целом будет выше в течение
некоторого последующего периода.
В ранних исследованиях экономических колебаний
предпочтение отдавалось детерминистским теориям, согласно
которым экономические циклы появляются с устойчивой
регулярностью, причем для всех циклов характерны одни и те же
свойства. Однако дальнейшие исследования показали, что данная
посылка не соответствует реальности.
В противоположность детерминизму импулъсно-
распространительный подход предполагает, что экономические
циклы являются следствием случайных воздействий (импульсов),
которые вызывают в экономике циклическую модель отклика. Сила
такого отклика со временем ослабевает (то есть цикл "угасает"),
однако деловые циклы возникают вновь вследствие появления новых
импульсов. Таким образом, цикличность развития экономики есть
результат воздействия серии последовательно возникающих
независимых импульсов (называемых также шоками).
Различают три типа шоков: шоки предложения, политические
шоки и шоки в спросе частного сектора.
К первым в теории циклов относят колебания мировых цен на
сырье и открытие новых источников сырья, технологические сдвиги,
природные катаклизмы.
Ко вторым относят импульсы, являющиеся следствием
политических решений, имеющих макроэкономический характер, и
воздействующие преимущественно на совокупный спрос. Это могут
быть изменения предложения денег, обменного курса, фискальной
политики.
Третьи представляют собой изменения инвестиционных или
потребительских расходов, вызванные переменами в ожиданиях
экономических субъектов.
В заключение главы следует отметить необходимость
проведения антициклической политики, посредством проведения
налогово-бюджетной (см.тему 9.2), денежно-кредитной (см. тему
10.4), внешнеторговой (см. тему 22.4), социальной (см. тему 18.4) и
др. видов политики для стабилизации экономики (сглаживания
экономических циклов) и увеличения экономического роста.
