Hua C., Wong R. Differential Equations and Asymptotic Theory in Mathematical Physics
Подождите немного. Документ загружается.


62
c) the integral
+W
j(x)
=
~cp(x)
=
1
cp(t)e-?dt
converges for
x
E
V
(the sector
V
being bisected by
R+
with opening
>
7r
=
f).
Then, by definition
f(x)
=
Lcp(x)
is
the Borel-sum
of
f^
in the
direction
R+.
In the next paragraph, we will recall basic facts about Laplace trans-
form.
Using the first (abstract) definition of k-summability, it is evident to
check the following.
Proposition
1.3.
Let
k
>
0.
Let d
a
fixed direction. The set
@{x}*,~
is
a
C-sub-digerential algebra
of
C[[x]];.
Definition
1.6.
If
f
E
@[[XI]
is k-summable in all the directions but
perhaps
a
finite set, we will say that it is k-summable and will denote
f
E
@{x}*.
Proposition
1.4.
(i)
Iff
is
k-summable
in
all
the directions, then
f
is
convergent (and conversely).
(ii)
@{x};
is a sub-diflerential algebra
of
@[[XI]*.
Remark
1.3.
The inclusion
@{x}l;d
c
@[[z]]l
is strict.
Indeed, consider
f
E
@[[x]]1
such that
Bf
=
@
admits a radius of
convergence
1
with the circle of center
0
and radius one as a natural cut.
Then it is not possible to extend
cp
analytically along
d
and
f
@
@{x}l,d.
A
similar argument can be used to prove that the inclusions
@{z};,~
c
@[[XI];
are all strict.
1.4.
Laplace
transform
Fourier transform.
We will use
real
conjugated variables
t
and
<.
Let
‘p
E
L’(R)
(t-line). We set
+m
Fcp(E)
=
@(E)
=
1
cp(t)e-itEdt.
-W
An important result is the
inversion
formula:

63
A
suficient
hypothesis is that
‘p
and
@
E
L1(R). It
is sufficient to suppose
that
‘p
E
C2(R)
and that
‘p, ‘p’, ‘p”
E
L1(R)
(then
@
E
0(1/t2)).
Laplace transform.
Let
‘p
E
C2([0,
+m)).
We will suppose that
Iq(t)I
I
AeBt
on
R+
(1.4.1)
for some positive
A,
B
>
0.
Then the integral
L‘p(z)
=
l+w
‘p(t)e-tzdt(= .F[’p(t)e-atIp+](z))
is convergent for
z
E
C,
Re
z
>
B.
Here, we set
z
=
u
+
it
and we denote
by
IR+
the characteristic function of
Rf
c
R.
We suppose that we have for
‘p,
‘p’,
‘p”
estimates of type
(1.4.1),
and
moreover:
‘p(0)
=
~’(0)
=
‘p”(0)
=
0.
Then using
Fourier inversion for-
mula,
we get
1
a+im
v(t)
=
/
L‘p(z)eztdz.
a-am
By direct computations:
1 1
2
22
L(1)
=
-,
L(t)
=
-
and
etz
22
-dz
=
Res(0,
-)
=
t
(u
>
0);
22
L(t
)
=
-,
23
The Laplace transform in the complex plane
Proposition
1.5.
The Laplace transform
C
;
‘p
--f
g
is an isomorphism
between two spaces:
(i) Holomorphic functions
‘p
on an unprecise (narrow) sector
C
=
{IArgtl
<
E}
(E
>
0)
with an exponential growth of order one and finite
type at
infinity
in
this sector:
I‘p(t)l
5
AeBltl
and admitting an asymptotic expansion at
0:
m

64
(ii)
Holomorphic functions
g
in
an unprecise sector
and admitting an asymptotic expansion at
00
in
this sector:
Moreover we have
an+l
=
n!
b,.
We have
(cf.
Fig. 1.4.1):
c+im
Fig 1.4.1
From complex Laplace transform, we get the Borel-Laplace formalism.
We use the conformal transformation
z
=
$
(automorphism of
C*
=
C
-
(0)).
We set
g(z)
=
f(x).
We have (cf. Fig. 1.4.3):
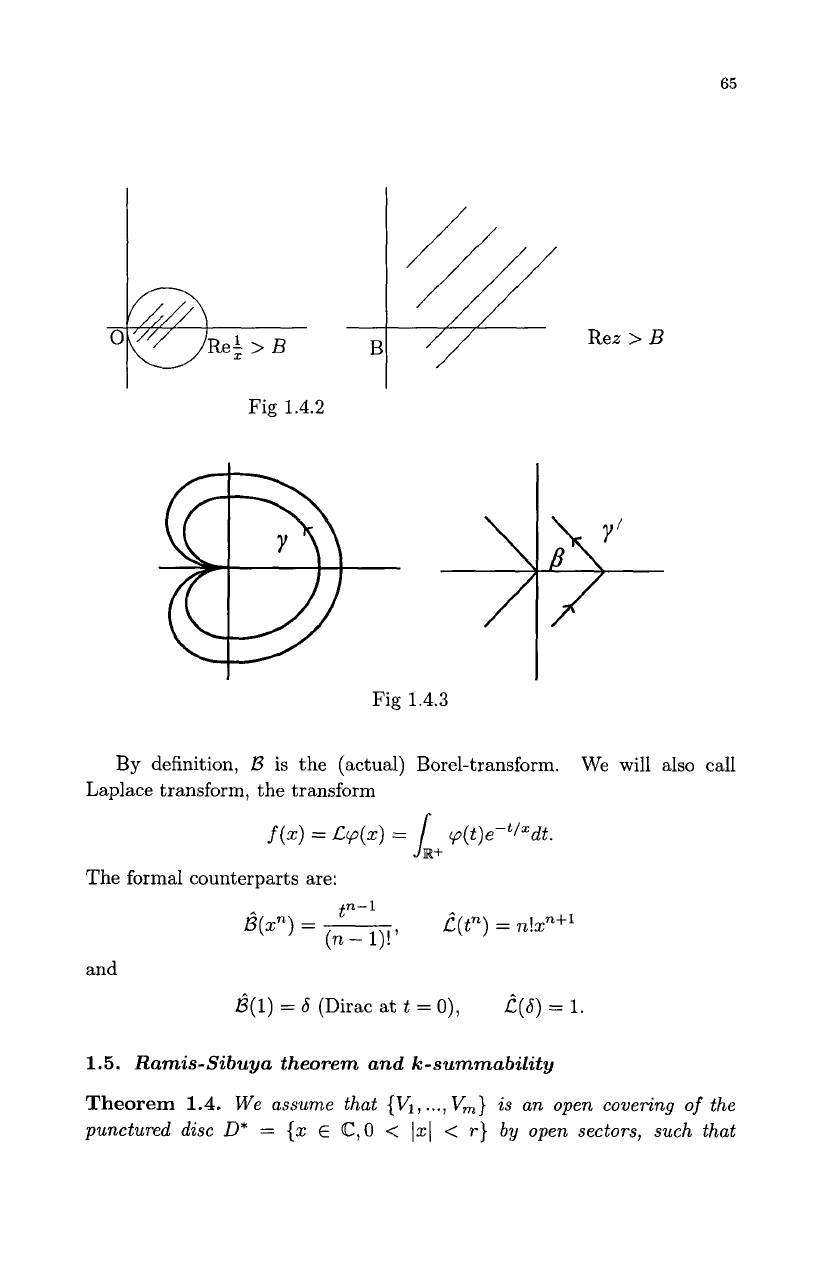
65
Fig
1.4.2
I
Fig
1.4.3
By
definition,
B
is the (actual) Borel-transform. We will also call
Laplace transform, the transform
The formal counterparts are:
tn-1
B(x")
=
_____
E(tn)
=
n!xnf1
(n
-
I)!'
and
g(1)
=
6
(Dirac at
t
=
0),
c(6)
=
1.
1.5.
Ramis-Sibuya theorem and k-summability
Theorem
1.4.
We assume that
{V1,..,,Vm)
is
an open covering
of
the
punctured
disc
D*
=
{x
E
@,O
<
1x1
<
r}
by
open sectors,
such
that

66
the three by three intersections are void. Let
f1,
...,
fm
be a collection
of
holomorphic functions satisfying the following conditions:
(i)
each
fj
E
O(V,)
is
bounded on
V,
(j
=
1,2,
...,
m);
(ii)
fj,j+l
=
fj+l-
fj
E
A<’(V,,j+,)
(j
=
1,2,
...,
m;
“m+l
=
1”;
V,,j+l
=
Then there exists a unique formal power series
f^
E
C[[x]]
such that the
V,
n
V,+d
fj
’S
admit
f^
as asymptotic expansion (in the classical sense) on the
V,
’s.
Moreover, let
k
>
0.
If
(ii)
is
replaced
by
(ii)’
fj,j+l
E
As-k(Y,j+i)JA
then
f^
E
@[[XI];
and
fj
N
f
in
Gevrey
Corollary
1.1.
If
fj
E
A<’(V,)
and
fij
E
ds-k(K,j),
then
fj
E
As-‘(&),
that is
the
fj’s
admit an exponential decay
of
order
k
on the
sense on
V,
(j
=
1,2,
...,
m).
V,
’s.
This result is named “Ramis
-
Sibuya Theorem”. The statement with
hypothesis (ii) is due to Malgrange. The corollary is due to Sibuya. The
statement with hypothesis (ii)’ is due to Ramis. The proof that we will
sketch below is due independently to Ramis and Sibuya. (Malgrange’s
argument was quite different.)
Lemma
1.3.
Let
{Vl,
...,
Vm}
be a covering
of
the punctured disc
D;l
(R
>
0)
by open sectors. (We suppose that
3
by
3
intersections are void.) Let
cpj,j+l
E
As-’((V,,j+l)
(‘h
+
1
=
1”)
be a given family
of
functions
(j
=
1,2,
...,
m).
Then (reducing
R
>
0
if
necessary) there exists a family
of
functions
{cpj}j=1,2
,...,
m,
such that:
(i)
‘pj
E
A(V,)
(j
=
1,2,
...,
m).
(ii)
cpj+l
-
cpj
=
cpj,j+l
(j
=
1,2,
...,
m;
“m
+
1
=
1
”).
Moreover,
if
cpj,j+l
E
AS-k(V,,j+l)
(j
=
1,2,
...,
m),
then
(i)”pj
E
A$(%)
(j
=
1,2,
...,
m).
Proof.
By linearity, we can suppose that
cpj,j+l
=
0
except for
j
=
1,
j
+
1
=
2. Then we set
’pl,~
=
g,
and
V1,2
=
Vl
n
V2;
V
=
{x
E
@,a
<
argx
<
,B,
1x1
<
R}.
We have
,B
<
a
+
27r. We will consider “ramified
sectors” (using the Riemann surface
of
the Logarithm). In particular we
introduce the ramified sector
=
{x
E
o*,
argx
E
[a,
,B
+
27r]}.
(cf. Fig
1.5.1
)
We choose
0
<
r
<
R
and denote
y
=
[0,7ei6]
the corresponding seg-
ment, for a fixed direction of argument
S
E
[(.,PI.
For
a
<
6
<
6’
<
p,

67
Fig
1.5.1
we set
y’
=
[0,7ei6‘].
Let
p’
be the circle arc joining
reib
to
Tei6’.
We
introduce
and
h,!,
h,!
by
analog formulae.
Fig
1.5.2
By
Cauchy integral formula, we get
h,,
-
h,,
-
h,
0
for
z
not belonging to the “triangular” domain delimited
by
y,
p’,
7’.
The
function
h,(z)
is
defined
on
C
-
y,
in particular for arg
5
E
(y,
y
+
27r).
For
z
such that arg
z
E
(y,
y
+
27r),
we can replace the contour of integration
y

68
by
pl
+
yl,
without changing h,(x):
hy(x)
=
hp‘(X)
+
h,’(X).
’
But
h,,
(x)
+
h,!
(x) is defined and holomorphic for x such that 1x1
<
T
and
Therefore we get an analytic extension
of
hy(x) to the ramified sec-
tor {x
E
d*
:
1x1
<
T,
argx
E
(6,s’
+
27r)).
Moving
6’
and therefore
yl
towards argx
=
p,
we get an analytic extension to the ramified sector
(1x1
<
T,
argx
E
(6,p
+
2~)).
Then we can suppose
a
<
6’’
<
6
<
p
and
move
6”
towards
a.
By
a similar argument, we get an analytic extension of
h,
to the ramified
sector:
{
1x1
<
T,
arg
2
E
(a,
p
+
2.)).
We denote
h
this extension. Let x be
such that
a
<
Algx
<
P.
We choose
b’,
6”
such that
a
<
S”
<
arg x
<
S’
<
P.
We consider the closed simple contour
y”
f
p”
-
p
-
y”
(oriented posi-
argx
E
(y1,y’+27r).
tively). By the Cauchy integral formula, we get
and g(x)
=
h(e2i“x)
-
h(x).
The function
g
is the variation of
h.
In
order to end the
proof
of Lemma
1.3,
it remains to prove asymptotic estimates for
h.
We can choose freely
y
with argx
E
(alp)
and prove such estimates for
h,
and
a
sector
W
corresponding to argx
E
[S
-t
E,
6
+
27r
-
E]
(E
>
0).
We write
xp xn
1
n-
1
1
-=-
therefore
We set

69
and we have
Because
I
argz
-
61
2
E,
we have
(tei6
-
21
2
1x1
sin&, therefore
The function
g
being infinitely flat at
0,
we have
therefore
It
follows that
If,
moreover,
g
E
d<-'(V),
then
(g(teib)I
I
ke-:
for some
K,
B
>
0,
and it follows:
We have
B-n+l
n-2
-pd
P
e
CL,
t-ne-B
t
dt
=
Our estimates follow easily; we can do similar computations for any
k
>
0.
This
ends
the
proof
of
Lemma
1.3.
This lemma implies easily Theorem
1.4.
We
apply Lemma
1.3
with
(pi,i+l
=
fi,i+l
=
fi+l
-
fi.
We get a family
of functions
{(pi}i=l,..,m,
'pi
E
d(V,)
(or
.A$(&))
such that
(pi,i+l
=
(pi+l-

70
Pi.
Then we get
pi+l
-
Pi
=
fi+i
-
fil
and
‘pi+l
-
fi+l
=
‘pi
-
fi
on
V,,i+l
=
V,
n
V,+l.
We set
$i
=
‘pi
-
fi
on
V,.
We have
$i
=
$i+l
on
V,
n
K+l,
therefore the
$is
(i
=
1,
...
m)
define
a
holomorphic function
$Ji
on
D*
=
U
V,.
z=l,
...
m
By hypothesis the
f,!s
are bounded, therefore
$J
is bounded on
D*
and
(Riemann’s extension theorem) can be uniquely extended to
a
function
$
holomorphic on
D
:
$
E
@{a:}.
Then
fi
=
‘pi
+$J
and
fi
E
d(V,)
(dt,(V,)),
which ends the proof of Theorem
1.4.
We can now
go
back to the study of k-summability. We recall that
f
E
@[[a:]]
is k-summable
(k
>
0),
if it is k-summable in every direction
d
but perhaps a finite number (the so-called singular directions off:
dl,
...
de).
The finite set
C(f)
=
{dl,
de}
is
the singular support of
f;
C(f)
=
0
H
f
E
@{a:},
i.e.
convergent.
It’s easy to see that, when
d
moves between two consecutive singular
directions
di
and
di+l,
then the sums
fd
off in the direction
d
give together
analytically and define a holomorphic function
fi
on a “sector”
%lo
(cf. Fig
1.5.3)
:
7r
7r
arga:
E
(argdi
-
-,argdi+l+
-).
2k
2k
Fig
1.5.3
“it
is an eye-shaped sector, the radius
1x1
can tend to zero when args
+
arg
di
-
&
or
arg
di+l
+
&
;
it
can be ramified.

71
The functions
fi
and
fi+l,
(i
=
1,
...,
i?
-
1)
have the same asymptotic
expansion at the origin:
fi,
fi+l
N
f”,
in Gevreyi sense. Therefore
fi+l
-
fi
=
fi,i+l
is asymptotic to zero on
V,,i+l
=
V,
fl
V,+l
in Gevrey
$
sense
(i.
e.
is exponentially decreasing with an order
k).
The eye-shaped “sector”
&+I
admits an opening exactly equal to
i.
There is a converse to this property which
(
even if it seems surprising)
will give
a
very efficient way to prove that a power series derived from a
problem of dynamical system is k-summable.
Theorem
1.5.
We assume that
{Vl,
...,
V,}
is an open covering
of
the
punctured disc
D*
by
open sector, such that the
3
by
3
intersections are
void. Let
{
f1,
...,
f,}
be a collection
of
holomorphic functions satisfying
the following conditions:
(a) each
fj
E
O(V,)
is bounded on
V,
(j
=
1,
...,
m);
(ii)
fj,j+l
defined
in
V,,j+l
=
V,
n
&+I
can be extended
in
an holomorphic
function defined on an eyeshaped ((sector” with opening
2
such that
Then there exists a unique formal power series
f”
such that
fj
N
f^
(i
=
1,
...,
m).
Moreover
f”
is k-summable and the
fls
correspond to sums
off
in
diferent directions.
If
we denote by
C
the finite set
of
the bisecting
lines
of
the sectors
&,i+l(i
=
1,
...,
m),
then
C(f”)
c
C.
this extension (denoted also
fj,j+l)
satisfies
fj,j+l
E
A-
<-k
(
v‘
j,j+l).
Proof.
We leave it to the reader (it is easy, using Theorem
1.4)
and
our definition of Ic-summability.
In the case of dynamical systems, it is in many cases possible to find
directly the
fis
using dynamical methods. Then it remains to estimate the
differences
fi+l
-
fi
=
fi,i+l
in order to prove an exponential decay (of
some order).
It
is important to notice that it is easy to linearize this last
problem, therefore the method is very powerful for non-linear problems.
Examples.
We will describe in some details two k-summable series. We
will begin with
our
favorite example: the Euler series. The next example
will be
a
power series coming &om the asymptotic expansion of the Airy
function at infinityll.
+m
=n
Euler series.
We start from
f(z)
=
C
(-l)”n!z”+’.
Here
k
=
1.
Its
.-
-
,.A
formal Bore1 transform is
B
f
(t)
=
&
=
1
-
t
+
t2
-
. .
. .
By 1-summation
llFor
more
details and other examples from special functions theory, cf. [Mar Ram].
