Hua C., Wong R. Differential Equations and Asymptotic Theory in Mathematical Physics
Подождите немного. Документ загружается.

362
Example
2
Same problem with
X
x3
x
t
-
5t2
+
14t3
-
t4
120
f(x,t)
=
-
1
+x'
cp(z)
=
7
-
5,
g(t)
=
1
&
=
0.01
,
0
<t
5
10
We can not find exact solution for this problem. By finite difference
method (FDM) we solve the direct problem and obtain the approximate val-
ues of u(x,t) in net points. Using these approximate values
at
x=0.3,0.5,0.7
as
measurements to solve the inverse problem we obtain the 5-th polynomial
approximation
of
the free boundary:
s(t)
=
-0.19232
+
0.0767t2
+
0.0893t3
-
0.0060t4
-
0.00005t5
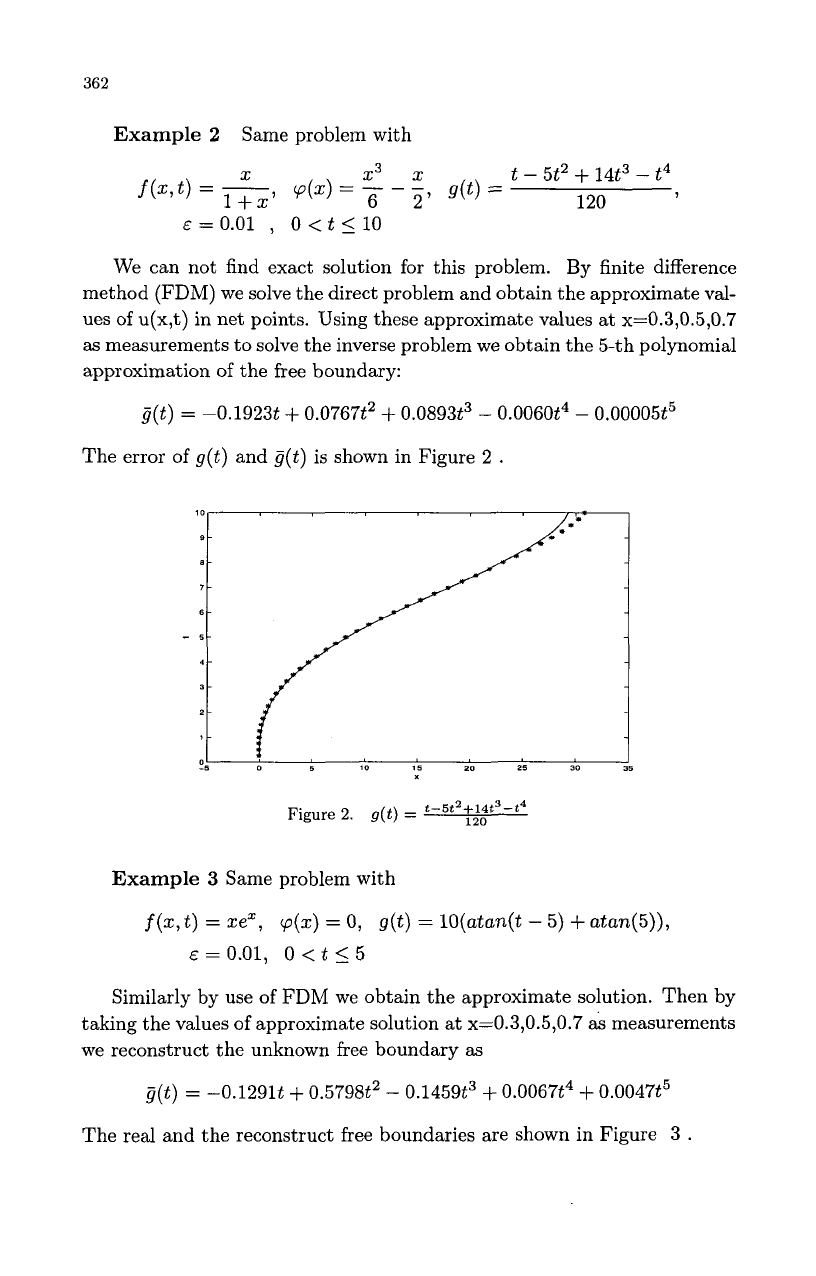
The error
of
g(t)
and
g(t)
is shown in Figure
2
.
Figure
2.
g(t)
=
t-5t2f;04t3-t4
Example
3
Same problem with
f(x,t)
=
ze",
p(x)
=
0,
g(t)
=
lO(atan(t
-
5)
+
atan(5)),
&
=
0.01, 0
<
t
5
5
Similarly by use of
FDM
we obtain the approximate solution. Then by
taking the values of approximate solution at
x=0.3,0.5,0.7
&
measurements
we reconstruct the unknown free boundary
as
s(t)
=
-0.1291t
+
0.5798t2
-
0.1459t3
+
0.0067t4
+
0.0047t5
The real and the reconstruct free boundaries are shown in Figure
3
.

363
Figure
3.
g(t)
=
lO(atan(t
-
5)
+
atan(5))
5.
Some Theoretical Results
Finally we give some related theoretical results to show that the existence
and the uniqueness of the solution for the direct corrosion problem and the
formal perturbation solution is really an asymptotic solution
.
Theorem
1(
Existence and uniqueness). Suppose that
s(t)
is continu-
ously differentiable in
[0,
TI,
vanishes at
t
=
0,
and has
a
low bound
c
>
-1
;
suppose that
f
(x,
t)
vanishes at
x=O
and is
Holder
continuous about
x
uniformly in
fi
(R
=
(0
<
t
5
T,O
<
2
<
1
+
~(t)}),
and suppose
cp(x)
is
continuously differentiable in
[0,1]
and vanishes at
x=O
.
Then the corrosion
boundary problem
in
R
-_
Ou.
a2u.
-
f(x,t)
4x1
0)
=
P(X)
on
[Olll
(8)
at
z?
-
du
i
U(0,t)
=
0
lz=l+s(t)
=
0
in
(O,T]
exists
a
unique solution
.
Based on the result
of
[4],
the proof
of
this theorem is not difficult.
Theorem
2
.
Denote
D1
=
(0,l)
,
521
=
(0,l)
x
(O,T]
,
and
02
=
(0,2)
x
(0,
TI
.
Let
R
=
(0
<
t
5
T,
0
<
x
<
1
+Eg(t)
}
and
R
2
R2,
and
E
be
small enough
.
Let
f,fz
E
C,(i=l2)
and
f(0,t)
=
0,
cp(x)
E
C3+,(.&)
and
cp(0)
=
cp,(l)
=
cp,,(O)
=
0,
and
g(t)
E
Cl+a([O,T])
.
Then the solution
u(x,t)
of the corrosion boundary problem
(2)
has an asymptotic expand
about
E
as
u(x,
t)
=
uo(z,
t)
+
&ul(x,
t)
+
o(E~)
in
fi1
n
il
where
~0(x,t)
is the solution
of
(3)
,
and
uI(x,t)
is the solution of
(4) .

364
References
1.
Karstein Sorli, Inge M.Skaar, Monitoring the wear-line
of
a
melting furnace,
Inverse problems in Engineering
:
Theory and Practice 3rd 1nt.Conference on
Inverse Problems in Engineering, June
13-18, 1999,
Port Ludlow, WA.USA
2. John Ockendon, Sam Howison, Andrew Lacey, Alexander movchan, Applied
Partial Differential Equations(revised edition)
,
Oxford university press,
OX-
ford,
2003
3.
John Hinch, Perturbation methods, Cambridge University Press, Cambridge,
1991
4.
Avner Friedman, Partial differential equations
of
parabolic type, Prentice
Hall, Englewood Cliffs,
1964

EXISTENCE AND STABILITY
OF
LAMELLAR AND
WRIGGLED LAMELLAR SOLUTIONS
IN
THE DIBLOCK
COPOLYMER PROBLEM
JUNCHENG
WE1
Department
of
Mathematics
Chinese University
of
Hong Kong
Shatin, Hong Kong
E-mai1:weiQmath. cuhk. edu. hk
We consider the lamellar phases in the diblock copolymer system which can be
written
as
a system of elliptic equations. Using r-convergence, the existence and
stability of K-interface solutions in
1D
are characterized. Then these solutions
extend trivially to
2D
and
3D
to become perfect lamellar solutions. The stability
of these lamellar solutions is completely characterized by obtaining the asymptotic
expansions
of
their eigenvalues and eigenfunctions. Consequently we find that they
are stable, i.e. are local minimizers in space, only if they have sufficiently many
interfaces. Interestingly the
1-D
global minimizer is near the borderline
of
3-D
sta-
bility. Finally using bifurcation analysis, we find wriggled lamellar solutions
of
the
Euler-Lagrange equation of the total
free
energy. They bifurcate from the perfect
lamellar solutions. The stability of the wriggled lamellar solutions is reduced to a
relatively simple finite dimensional problem, which may be solved accurately by a
numerical method. Our tests show that most of them are stable. The existence of
such stable wriggled lamellar solutions explains why in reality the lamellar phase
is
fragile and it often exists in distorted forms.
Key
words
diblock copolymer, r-convergence, lamellar solutions, distortion, sta-
bility, wriggled lamellar solution, perfect lamellar solution,
2000
Mathematics
Subject Classification
58307,35J55,34Dl5,45J05,82D60
1.
Introduction
In this article, we review and summarize recent advances on the study
of
diblock copolymer system.
A
diblock copolymer is a
soft
material, charac-
terized by fluid-like disorder on the molecular scale and a high degree
of
order at longer length scales.
A
molecule in a diblock copolymer melt is
linear sub-chain
of
A
monomers grafted covalently to another sub-chain
of
B
monomers. Because
of
the repulsion between the unlike monomers, the
different type sub-chains tend to segregate below some critical temperature,
365

366
but
as
they are chemically bonded in chain molecules, even a complete seg-
regation of sub-chains cannot lead to a macroscopic phase separation. Only
a local micro-phase separation occurs: micro-domains rich in
A
and
B
are
formed. These micro-domains form morphology patterns/phases in
a
larger
scale. The most commonly observed undistorted phases are the spherical,
cylindrical and lamellar, depicted in Figure
1.
Here we seek undistorted or
distorted, lamellar patterns.
We consider a scenario that a diblock copolymer melt is placed in a
domain
D
and maintained at fixed temperature.
D
is scaled to have unit
volume in space. Let
a
E
(0,l)
be the relative number of the
A
monomers in
a chain molecule, and
b
=
1
--a
be the relative number of the
B
monomers in
a
chain. The relative
A
monomer density field
u
is an order parameter.
u
M
1
stands for high concentration of
A
monomers. The melt is incompressible
so
the relative
B
monomer density is
1
-
u
and
u
M
0
stands for high
concentration of
B
monomers.
S
phase
C
phase
L
phi
Figure
1.
The spherical, cylindrical, and lamellar morphology phases commonly
ob-
served in diblock copolymer melts. The dark color indicates the concentration
of
type
A
monomer, and the white color indicates the concentration
of
type
B
monomer.
Ohta and Kawasaki [14] introduced an equilibrium theory, in which the
free energy of the system is a functional
of
the relative
A
monomer density:
E2
I(u)
=
~{T~VUI~
+
Yl(-A)-1/2(u
-
.)I2
+
W(u)},
(1.1)
defined in
X,
=
{u
E
W1i2(D)
:
?i
=
a},
where
?i
:=
sDu
is the average
of
u
on
D.
The original formula in [14] is given on the entire
R3.
The
expression here on a bounded domain
D
first appeared in Nishiura and
Ohnishi
[12].
The local function
W
is smooth and has the shape of a double
well.
It
has the global minimum value
0
at two numbers:
0
and
1.
To avoid
unnecessary technical difficulties we assume that
W(p)
=
W(l
-
p).
The

367
two global minimum points are non-degenerate:
W"(0)
=
W"(1)
#
0.
It
reflects the connectivity of polymer chains.
of the positive operator
(-A)-'
from
{w
E
L2(D)
:
integral of the nonlocal part in
(1.1)
may be rewritten
as
The most unusual in
(1.1)
is the nonlocal expression
(-A>-'I2(u
-
u).
is the square root
=
0)
to itself. The
GD
is the Green function of
-A
with the Neumann boundary condition.
It
splits to
a
fundamental solution part and a regular part. The fundamental
solution in
R3
is
&,
a long range Coulomb type interaction, which is
common in many important physical systems (Muratov
[lo]).
E
and
y
are positive dimensionless parameters that depend on various
physical quantities.
In the strong segregation region where morphology
patterns form,
E
is very small.
y
is of order
1
when we choose the size
of
the sample to be comparable to the size of the microdomains. We de-
velop a particular two parameter perturbation method.
We do singular
perturbation analysis with respect to
E
and bifurcation analysis with re-
spect to
y.
The challenge is to combine these two techniques to derive fine
analytical results. Even though this mathematical method
is
tailored
for
the diblock copolymer problem, we believe that it may be applied to other
ones with multiple parameters. Examples include the Seul-Andelman mem-
brane problem
[22,26],
charged Langmuir monolayers
[2,23],
and smectic
films
[24,25].
The Euler-Lagrange equation of
I
is
-f2Au
+
f(u)
-
fo
+
ET(-A)-'(U
-
U)
=
0,
a,u
=
0
on
dD.
(1.2)
-
f
is the derivative of
W.
The term
f(u)
is equal to the Lagrange multiplier
corresponding to the constraint
E
=
a.
The equation
(1.2)
may also be
written as an elliptic system:
-e2Au
+
f(u)
+
~yv
=
Const.
w=u-u
(1.3)
{
a,u
-A
=
a,W
=
0
on
aD,
u
-
u
=
v
=
0.
Here Const. is the Lagrange multiplier.
From now on, we shall concentrate on the study of
(1.3).
To
avoid
clumsy notations a quantity's dependence on
E
is usually suppressed.
For
example we write
u,
the lamellar solution, instead
of
u,.
On the other hand
we often emphasize a quantity's independence of
E
with a superscript
0.
For
example the limit of a lamellar solution
u
as
E
4
0
is denoted by
uo.
In

368
1
1
0.9
0.9
08
08
07
07
06 0.6
05
05
04
04
03 0.3
02
02
0.1
0.1
0
0
0
02
04
06
0.8
1
0
02
0.4
06
08 1
Figure
2.
A
perfect lamellar solution and
a
wriggled lamellar solution. In the dark
regions the solutions are close to
1
and in the light regions the solutions are close to
0.
estimates
C
is always a positive constant independent of
E.
Its value may
vary from line to line. The
L2
inner product is denoted by
(.,
.)
and the
LP
To simplify the formulation of our results, we take
D
=
(0,l)
x
(0,l)
to
be
a
2-D
square instead of a
3-D
box. Generalization to
3-D
is trivial.
References on the mathematical aspects of the block copolymer theory
include, in addition to the ones cited already, Ohnishi
et a1
[13],
Choksi
[3],
Choksi and Ren
[4],
Fife and Hilhorst
[6],
Henry
[7],
Ren and Wei
[16,17,21],
on diblock copolymers, and Ren and Wei
[19,20]
on triblock copolymers.
norm by
II
. Ilp.
2.
One-dimensional
Local
Minimizers
First, we consider
(1.3)
when
D
=
(0,l).
In Ren and Wei
[15]
a
family
of
lamellar solutions is found. When
D
=
(0,
l),
for each positive integer
K
there exists a 1-dimensional local minimizer of
I
if
E
is sufficiently small.
The findings there are summarized in the following theorem.
Theorem
2.1.
[Ren and
Wei
[15]]
In
1-D
for
each positive integer
K
the
functional
in
{u
E
W132(0,
1)
:
u
=
a}, has a local minimizer
u
near
uo,
under the L2
norm, when
E
is
suficiently small. It satisfies the Euler-Lagrange equation

369
and has the properties
Let
H
be the solution
of
-HI'
+
f
(H)
=
0
in
R,
H(-oo)
=
0,
H(m)
=
1,
H(0)
=
1/2.
(2.1)
The constant
T
in the theorem is defined by
T
:=
L(HI(t))'dt.
T
is often called the surface tension in the literature.
uo
is a
step function
of
K
jump discontinuity points, defined to be
uo(x)
=
1
on
(o,x:),
O
on
(x:,xi),
1
on
(xi,xg),
o
on
(x,",xi),
1
on
(x,",x!)
,...
with (recall
b
=
1
-
a)
(2.3)
a
l+b
2+a
3+b
4+a
,
x5=-
,x4=-
K'
K
K
K
'
*'*'
K
x!+- x$-
,
x3=-
Go
is the solution operator of
-v"
=
g,
v'(0)
=
v'(1)
=
v
=
0,
i.e.
v
=
There is another K-interface
1-D
local minimizer whose limiting value
as
E
+
0 is 0 instead of
1
on the first interval
(0,
b/K).
It
is just
1-ii
where
ii
is a solution constructed in Theorem
2.1,
but with
=
b
instead.
1
-
ii
has the same properties as
u
does,
so
we focus on
u. u
is found periodic in
the following sense.
Go[g]
=
(-&)-%.
Theorem
2.2.
structed
in
Theorem
2.1.
When
E
is small,
for
every
x
E
(0,1/K),
[Ren and Wei
[lS]]
Let
u
be
a
1-D
local minimizer con-
u(x)
=
u($
-
x)
=
u(x
+
$)
=
U(R
4
-
x)
=
u(x
+
+)
=
...
u(1
-
x)
if
K
is even
={u(x+y)ifK
isodd.
Moreover when
E
is small,
u
is the unique local minimizer
of
I1
in
an
L2
neighborhood
of
uo.
If
u
on
((j
-
l)/K,j/K)
for
some
j
=
1,2,
...,
K
is
scaled to a function on
(0,
l),
then
it
is exactly a one-layer local minimizer
of
I1
with
E
and
y
replaced
by
2
=
EK
and
;Y.
=
y/K3.
Let us denote this
u
of
K
interfaces by
uy,
to emphasize its dependence
on
y.

370
Actually Theorem
(2.2)
is also true when
y
=
:.
See
[17].
We note
that when
a
=
i,y
=
f,
Muller
[9]
first proved the periodicity of global
minimizers under the condition that
W
is symmetric. Further attempts in
removing the condition
a
=
can be found in
[l],
[13],
where only partial
results are obtained.
3.
Stability of the Perfect Lamellar Solutions in
2D
We consider
D
=
(0,l)
x
(0,l).
The
1-D
local minimizer
uy
of
11
is now
viewed as
a
function on
D,
through extension to the second dimension
trivially,
so
uy(x,y)
=
u,(x).
It is
a
solution
of
(1.2)
and
Il(u,)
=
I(u,).
In
2-D
it has straight interfaces. We call it a perfect lamellar solution of
(1.2).
The linearized operator of
(1.2)
at
u,
is
(3.1)
L,c~
:=
-e2A(p
+
f'(u,)cp
-
f'(uy)P
+
~y(-A)-"p,
'p
E
W2v2(0),
a,'p
=
o
on
a~,
(P
=
0.
This is an unbounded self-adjoint operator defined densely on
{$
E
L2(D)
:
$
=
0}
whose spectrum consists of real eigenvalues only.
For an eigen pair
(X,'p)
of
L,
separation of variables shows that
'p(z,y)
=
$,(x)cos(m.rry)
where
m
is a non-negative integer. Hence the
eigenvalues
X
are naturally classified by
m.
We therefore denote
a
X
that
is associated with
m
by
A,.
-
Let
G,
be the solution operators
of
the differential equations
-XI'
=
$0,
~'(0)
=
~'(1)
=
0,
X
=
0,
if
m
=
0,
(3.2)
(3.3)
i.e.
G,[$,]
=
X.
We often identify the operators
G,
with the Green
functions of
(3.2)
and
(3.3).
Then we have following theorem which char-
acterizes
A,:
Theorem
3.1.
[Ren and Wei [18]]
a
The eigenvalues
X
of
L
are classified
into
A,
by
m
which is a non-negative integer. The following
3
statements
hold when
E
is suficiently small.
-XI'
+
m27r2X
=
$,,
~'(0)
=
~'(1)
=
0,
if
m
#
0,
(1) There exists
M(K)
depending on
K
but
not
E
so
that when
Iml
2
M(K),
A,
2
Ce2
for some
C
>
0
independent
of
E.
a
[18,
Theorem
1.11
is
formulated for a
3-D
box.
The
similar conclusions
hold true
for
the
2-D
square
D
here.

371
(2)
When
m
=
0,
there are
K
small positive
Ao’s.
One
of
them is
of
order
E
whose only eigenfunction is approximately
Cj
(hj
(x)
-
G).
The other
K
-
1
A0
’s
are
of
order
e2.
Their only eigenfunctions are
approximately
Cj
cj”hj(x)
for
some vectors co satisfying
Cj
cj”
=
0.
The remaining
AO’S
are positive and bounded below by a positive
constant independent
of
E.
(3)
When
m
#
0
and
Iml
<
M(K),
there are
K
Am’s
of
order
e2,
which
are not necessarily positive, whose only eigenfunctions are approxi-
mately
Cj
cj”hj(x)
cos(m7ry).
The remaining
A,,,
’s
are positive and
bounded below
by
a positive constant independent
of
E.
Only when
K
is suficiently large
or
y
is suficiently small, all the eigenvalues
of
L
are positive and
u
is stable.
The eigenvalues
A0
in Part
2
of
Theorem
3.1
are just the
1-D
eigenval-
ues
of
uy.
That they are positive is consistent with the fact that
uy
is
a
local minimizer
of
11.
Bifurcations occur at
0
eigenvalues,
so
we are more
interested in the
Am’s
of
Part
3.
In
[18,
Sections
6
and
71
we obtained
asymptotic expansions of the
K
pairs
(A,,,,
q5,,,)
in Part
3.
When m
2
1,
In
(3.4)
q5m
is decomposed to
Cj
cjhj
in
the subspace spanned by
hj,
j
=
1,2,
...,
K,
and
e2q5k
in the orthogonal complement
of
the subspace.
Moreover
11q5&112
=
O(lc1)
‘.
As
E
4
0,
cj
4
cj”.
Here
(A,co)
are the
K
eigenpairs of the
K
by
K
matrix
[G,(xY,
x“,].
[G,(xY,
x“,] is diagonalized
in
[18,
Section
71.
When
K
=
1,
it has,
for
each m
2
1,
one eigenvalue pair
co
0:
1. (3.5)
1
mr(tanh(mra)
+
tanh(mrb))
’
A=
When
K
=
2,
there are two eigenpairs
,co
0:
(-1, I),
1
A=
A=
1
co
0:
(1,l). (3.6)
mr(coth(maa)+cot(mrb)-CSCh
(rnra)+CSCh
(mrb))
rnr(coth(mxa)+cot(rnrb)-CSCh
(maa)-csCh
(mrb))
’
When
K
2
3,
there are
K
eigenpairs
1
A=-
,
co.
d-9
(3.7)
bSee
[18,
Formula
(6.55)).
