Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


15. (a)
(b)
(c)
17. {(ln x, ln y)} is approximately linear, so a power model is
appropriate.
19. {(ln x, ln y)} is approximately linear, so a power model is
appropriate.
21. (a)
(b)
92,000
08
105,000
f(x)
g(x)
92,000
08
105,000
0
40
0 20
0
10
0 20
0
5
0 20
1006 ANSWERS
(c)
(d) Answers will vary.
23. (a)
(b)
(c) An exponential model would be best:
y 148.55(.9700)
x
25. (a)
(b) y 73.59 (.8572)
x
(c) .7
(d) 2012
27. (a)
(c) y 1311520.25(1.02)
x
(e) 1,602,588
(d) (b)
Predicted Number
Adults on of Adults on
Year Probation Probation Ratio
2000 1316333 1311520 1.01
2001 1330007 1338073 1.03
2002 1367547 1365163 1.02
2003 1392796 1392801 1.02
2004 1421911 1420999
29. (a) y 21.34 12.64 ln x
(b) 79.03
(c) 2031
Chapter 5 Review, page 420
1. a
2
3. x
11/15
y
4/3
5. x
2/3
y
2/3
7.
2
y
x
3
2
9.
11. x 17/9 13. No solutions
15. x 1.733 or 5.521
17. 3 x 3 and 0 y 2
19.
21.
23. (a) About 2.03
(b) About 31.97
(c) Approximately 6 to 10 months
(d) Never; however, at the end of 18 months about 99.6%
of the program will be mastered.
25. ln 23 3.14 27. ln (4a b) x 7y
29. log 177 2.248 31. e
6.0014
404
33. e
15t
4xy 35. 6
y
3x 4
37. 2/3 39. x/2
41. ln x 43. ln (3/b
4
)
45. ln x
11
47. 2
49. (c) 51. (c)
2
−2
−4
y
x
−4
4812
h(x) = ln (x + 4) − 2
−1
6
4
2
y
x
−2−4
4
g(x) = 2
x
− 1
2
3
3x 3
h 5
3x 5
ANSWERS 1007
53. x 4 55. x 3 or x 6
57. x 1/3 59. x e
(3b2a)/c
61. x 3 63. x 48.5
65. About 1.64 mg 67. About 12.05 years
69. $3822.66 71. 7.6
73. (a) 11°F
(b)
(c) The ratios of successive entries are approximately
constant.
(d) f (t) 22.42e
.034x
.
(e) About 10°F
Chapter 5 Test, page 424
1. (a) (b) a
b
(c)
2. (a) x 2, x 1 3
(b) x 9, x 7
3. (a) 905 (b) 905 (c) 1105
4. (a) k is positive, because the function approaches zero as it
goes to the left, and gets larger as it goes to the right.
(b) 3
5. (a) 2 3
(b) (3
3
ab
)b
2
(c) a
2
b
3
6. (a) 32 million (b) 176,777 (c) 32.768 billion
7. $3247.30
8. Compute the following
(a) 4 (b) x h (c) 2276
9. 871 years old.
10. (a) x
2
y
2
(b)
b
a
2
(c)
1
3
11. A 3, B 2
12. (a) 1 (b) ln 2 (c) Can’t be simplified
13. A population of mayflies grows according to the equation
P 230e
.6t
where t is in days.
(a) 230 (b) 6.29 days
14. (a) y 120 15 ln x, where x is in months, and x 1
corresponds to January.
(b) 130.40,157.27
3(x
4)
x 16
(a b)(a
b
)
a b
2 h
2 h
28
0
50−1
Chapter 6
Section 6.1, page 434
1. 2p/9 3. p/9 5. p/18
7. About
p
3
9. About
4
3p
11.
9
4
p
,
17
4
p
,
4
7p
,
1
4
5p
13.
11
6
p
,
23
6
p
,
1
6
3p
,
2
6
5p
15. No 17. Yes 19. 5p/3
21. 3p/4 23. 3p/5 25. 7 2p
27. p/30 29. p/15 31. 5p/12
33. 3p/4 35. 5p/4 37. 31p/6
39. 36° 41. 18° 43. 135°
45. 4° 47. 75° 49. 972°
51. 4p/3 53. 7p/6 55. 41p/6
57. 7p 59. 4p 61. 42.5p
63. 2pk
Special Topics 6.1.A, page 440
1. 5 3. 8.75 5. 25.13 cm
7. 2.5 rad 9. 2 rad 11. 6
13. 15 15. 5.56 17. 2000
19. 3455.8 21. 933.1 23. 12.5 sq ft
25. 76.8 sq m 27. 2 rad 29. 2.4 rad
31. r 3978.8736 mi; c 25,000.0001 mi
33. 3
35. (a) 400p
m
ra
i
d
n
(b) 2513.3
m
in
i
.
n
; 209.4
m
f
i
t
n
37. (a) 5p
r
s
a
e
d
c
(b) 6.69 mph
39. 15.9 ft
Section 6.2, page 449
1. 1 3. 0 5. 0
7. 0 9. 0
11. sin t 1/5
, cos t 2/5
, tan t 1/2
13. sin t 4/5, cos t 3/5, tan t 4/3
15. 3
/2, 1/2, 3
17. 2
/2, 2
/2, 1
19. 2
/2, 2
/2, 1 21. 1/2, 3
/2,
3
3
23. sin
23
6
p
1
2
, cos
23
6
p
2
3
, tan
23
6
p
3
3
1008 ANSWERS
25. sin
19
3
p
2
3
, cos
19
3
p
1
2
, tan
19
3
p
3
27. sin
15
4
p
2
2
, cos
15
4
p
2
2
, tan
15
4
p
1
29. sin
17
2
p
1, cos
17
2
p
0,
tan
17
2
p
is not defined
31. 3
/2 33. 2
/2 35.
4
2
(1 3
)
37. sin t 5/34
; cos t 3/34
; tan t 5/3
39. sin t 5/41
; cos t 4/41
; tan t 5/4
41. sin t 8/67
; cos t 3/67
; tan t 8/3
43. (a) 467 mph (b) 1458 mph
45. (a)
(b)
47. 2/p 49.
7
3
p
1
51.
2
3p
2
53.
4
p
3
55. (a) .420686; .416601; .416192; .416151
(b) cos 2 .416147
57. sin t 2/5
; cos t 1/5
; tan t 2
59. sin t 5/34, cos t 3/34, tan t 5/3
61. sin t 1/5
, cos t 2/5
, tan t 1/2
63. Quadrant I: sin t(), cos t(), tan t();
Quadrant II: sin t(), cos t(), tan t();
Quadrant III: sin t(), cos t(); tan t();
Quadrant IV: sin t(), cos t(), tan t()
Date Jan 1 Mar 1 May 1
Average
Temperature 31.7 43.8 68.3
Date July 1 Sept 1 Nov 1
Average
Temperature 80.9 69.0 44.5
Date June 13 June 16 June 19 June 22
Average
Temperature 79.6 80.0 80.3 80.5
Date June 25 June 28
Average
Temperature 80.7 80.8
Date June 1 June 4 June 7 June 10
Average
Temperature 77.4 78.0 78.6 79.1
65. Positive since 0 1 p/2
67. Negative since p/2 3 p
69. Positive since 0 1.5 p/2
71. t
p
2
2pn, n any integer 73. t pn, n any integer
75. t
p
2
pn, n any integer
77. sin(cos 0) sin 1, while cos(sin 0) cos 0 1. Since
sin 1 1 (draw a picture!), cos(sin 0) is larger than
sin(cos 0).
79. (a) Each horse moves through an angle of 2p radians in 1
min. The angle between horses A and B is p/4 radians
(
1
8
of 2p radians). It takes
1
8
min for each horse to
move through an angle of p/4 radians. Thus the posi-
tion occupied by B at time t will be occupied by
A
1
8
min later, that is, at time t
1
8
. Therefore,
B(t) A
t
1
8
.
(b) C(t) A
t
1
3
.
(c) E(t) D
t
1
8
; F(t) Dt
1
3
.
(d) The triangles in Figure S are similar, so that
5
1
D
A(
(
t
t
)
)
. Therefore, D(t) 5A(t).
(e) E(t) 5B(t) 5A
t
1
8
; F(t) 5C(t) 5At
1
3
.
(f) Since horse A travels through an angle of 2p radians
each minute and its starting angle is 0 radians, then at
the end of t min horse A will be on the terminal side of
an angle of 2pt radians, at the point where it intersects
the unit circle. A(t) is the second coordinate of this
point; hence, A(t) sin(2pt).
(g) B(t) A
t
1
8
sin
2p
t
1
8
sin(2pt p/4); C(t) sin(2pt 2p/3)
(h) D(t) 5 sin(2pt); E(t) 5 sin(2pt p/4);
f (t) 5 sin(2pt 2p/3)
Section 6.3, page 464
1. ( fg)(t) 3 sin
2
t 6 sin t cos t
3. 3 sin
3
t 3 sin
2
t tan t 5. (cos t 2)(cos t 2)
7. (sin t cos t)(sin t cos t)
9. (tan t 3)
2
11. (3 sin t 1)(2 sin t 1)
13. (cos
2
t 5)(cos t 1)(cos t 1)
15. ( f g)(t) cos(2t 4), (g f )(t) 2 cos t 4
17. ( f g)(t) tan(t
2
2), (g f )(t) tan
2
(t 3) 1
19. Yes 21. No 23. No
25. sin t 3
/2 27. sin t 3
/2
29. 3/5 31. 3/5 33. 3/4
35. 3/4 37. 21/5 39. 2/5
41. 21/5 43.
2
2
2
45.
2
2
2
ANSWERS 1009
47. sin
2
t cos
2
t 49. sin t
51. sin t cos t sin t
53. 1/4
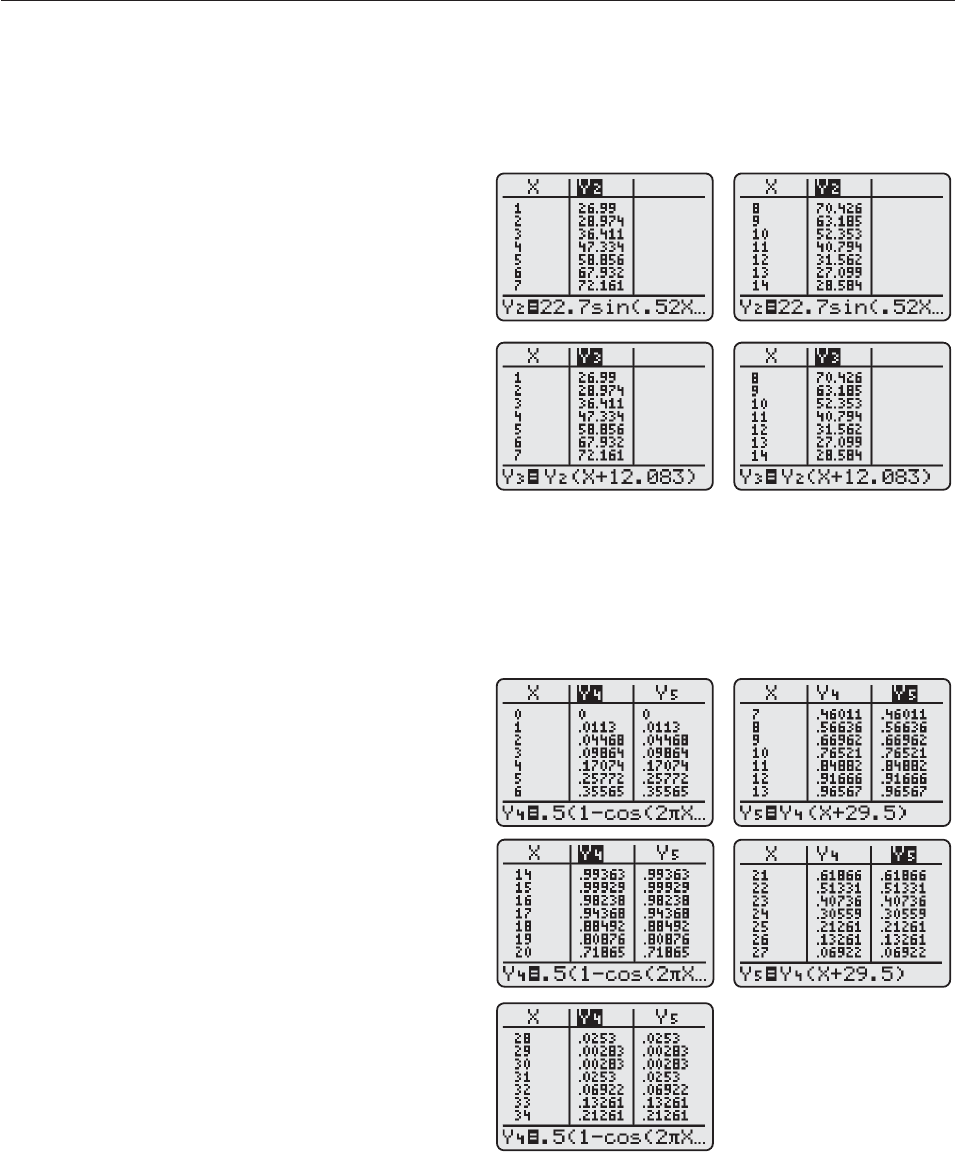
55. cos t 2 57. cos t
59. (a) Y
2
f(t) 22.7 sin(.52x 2.18) 49.6 and Y
3
f(x 12.083) 22.7 sin(.52(x 12.083) 2.18)
(b) Yes; the period is 12.083, which is a reasonable approx-
imation of the expected period of 12 months.
61. (a) 0; about 76.5%; about 51.3%
(b) Y
4
g(t) .5
1 cos
2
2
9
p
.5
t
and Y
5
g(t 29.5)
.5
1 cos
2p(t
2
9.5
29.5)
(c) Late on day 14 (t 14.75)
63. f(t k) cos 3
t
2
3
p
cos (3t 2p) cos 3t f (t)
65. f(t 2) sin (p(t 2)) sin (pt 2p) sin (pt) f(t)
67. f
t
p
2
tan 2
t
p
2
tan (2t p) tan (2t) f(t)
69. (a) There is no such number k.
(b) If we substitute t 0 in cos(t k) cos t, we get
cos k cos 0 1.
(c) If there were such a number k, then by part (b),
cos k 1, which is impossible by part (a). Therefore,
there is no such number k, and the period is 2p.
Section 6.4, page 474
1. t . . . , 2p, p, 0, p, 2p, . . . ; or t pk, where k is any
integer
3. t . . . , 7p/2, 3p/2, p/2, 5p/2, 9p/2, . . . ; or
t p/2 2pk, where k is any integer
5. t . . . , 3p, p, p, 3p, . . . ; or t p 2kp, where k is
any integer
7. 11 9. 1.4
11. Shift the graph of f vertically 3 units upward.
13. Reflect the graph of f in the horizontal axis.
15. Shift the graph of f vertically 5 units upward.
17. Stretch the graph of f away from the horizontal axis by a
factor of 3.
19. Stretch the graph of f away from the horizontal axis by a
factor of 3, then shift the resulting graph vertically 2 units
upward.
21. Shift the graph of f horizontally 2 units to the right.
23. D 25. B 27. F 29. G
31. 2 solutions 33. 2 solutions
35. 2 solutions 37. 2 solutions
39. Possibly an identity 41. Possibly an identity
43. Possibly an identity 45. Not an identity
47. Possibly an identity 49. Not an identity
51. No 53. Yes; period 2p
55. Yes; period 2p 57. No
59. No
61. (a) Yes if proper value of k is used; no
(b) 0, 2p, 4p, 6p, etc. So why do the graphs look identical?
63. (a) 80
(b) 14 or 15 on 96-pixel-wide screens; up to 40–50 on
wider screens; quite different from part (a). Explain
what’s going on. [Hint: How many points have to be
plotted in order to get even a rough approximation of
one full wave? How many points is the calculator plot-
ting for the entire graph?]
65. (a) p t p
(b) n 15; f
15
(2) and g(2) are identical in the first nine
decimal places and differ in the tenth, a very good
approximation.
1010 ANSWERS
67. r(t)/s(t), where r(t) f
15
(t) in Exercise 65 and
s(t) f
16
(t) in Exercise 66.
69. The y-coordinate of the new point is the same as the
x-coordinate of the point on the unit circle. To explain
what’s going on, look at the definition of the cosine
function.
Section 6.5, page 486
1. Amplitude: 3, period: p, phase shift:
p
2
3. Amplitude: 5, period:
2
5
p
, phase shift:
25
1
5. Amplitude: 1, period: 1, phase shift: 0
7. Amplitude: 6, period:
2
3
, phase shift:
3p
1
9. f(t) 3 sin
8t
8
5
p
11. f(t)
3
4
sin(pt)
13. f(t) 7 sin
6
5
p
t
3p
5
2
15. f(t) 2 sin 4t
17. f(t) 1.5 cos
2
t
19. (a) p/100
(b) The graph makes 200 complete waves between 0 and 2p.
(c) 0 x p/25; 2 y 2
21. (a)
9
2
0
p
0
(b) The graph makes 900 complete waves between 0 and 2p.
(c) 0 x
2
2
2
p
5
; 2 y 2
23. (a) f (t) 12 sin
10t
p
2
(b) g(t) 12 cos 10t
25. (a) f (t) sin 2t
(b) g(t) cos
2t
p
2
27.
1
−1
−3
3
−π−2π 2ππ
29.
31.
33. Local maximum at t 5p/6 2.6180; local minimum at
t 11p/6 5.7596
35. Local maxima at t p/6 .5236, t 5p/6 2.6180,
t 3p/2 4.7124; local minima at t p/2 1.5708,
t 7p/6 3.6652, t 11p/6 5.7596
37. A 3.606; b 1; c .5880
39. A 3.8332; b 4; c 1.4572
41. The waves do not have the same amplitude.
43. (a) The person’s blood pressure is 134/92.
(b) The pulse rate is 75.
45. (a) Maximum is 79.5 cubic inches; minimum is 30.5 cubic
inches.
(b) every 4 seconds
(c) 15
47. Period:
980
1
,000
seconds; frequency: 980,000
49. f (t) 125 sin(pt/5)
51. f (t) cos 20pt
16 s
in
2
(20p
t)
53. h(t) 6 sin(pt/2)
55. h(t) 6 cos(pt/2)
57. d(t) 10 sin(pt/2)
59. (a) At least four (starting point, high point, low point, end-
ing point)
(b) 301
(c) Every calculator is different; the TI-84 plots 95 points;
others plot as many as 239.
(d) Obviously, 239 points (or fewer) are not enough when
the absolute minimum is 301.
1
3
−1
−2
−3
2ππ
3π
22
π
2
π
2
h(t) = 3 sin 2t +
()
1
−1
−π−2π 2ππ
ANSWERS 1011
61. (a)
(b) The data appears to be approximately periodic. An ap-
propriate model is f(t) 1.1371 sin(.6352t .6366)
7.4960.
(c) No; the model is only a fair approximation of the data
and, in any case, unemployment is hard to predict.
(d) g(x) 24.85 sin (.52x (2.15)) 48.95
(e) 12.05 months, yes it fits better.
63. (a) f (t) 2.77
sin(.39x 1.91) 2.52
(b) f (x) has period 16.1. One would expect a period
of 12.
(c)
(d) g(x) 2.17 sin(.51x 1.04) 1.71
(e) g(x) has period 12.3, and it seems to fit better than f(x).
65. (a) k 9.8/p
2
(b) When k is replaced by (k .01% of k), the value of v
changes and the period of the pendulum becomes ap-
proximately 2.000099998 sec, meaning that the clock
loses .000099998 sec every 2 sec, for a total of approx-
imately 397.43 sec (6.62 min) during the three months.
Special Topics 6.5.A, page 496
1. A 2.2361, b 1, c 1.1071
3. A 5.3852, b 4, c 1.1903
5. A 5.1164, b 3, c .7442
7. 0 t 2p and 5 y 5 (one period)
9. 10 t 10 and 10 y 10
11. 0 t p/25 and 2 y 2 (one period)
13. 0 t .04 and 10 y 10 (one period)
15. 0 t 20 and 11 y 11 (one period)
17. To the left of the y-axis, the graph lies above the t-axis,
which is a horizontal asymptote of the graph. To the right of
the y-axis, the graph makes waves of amplitude 1, of shorter
and shorter period.
Window: 3 t 3.2 and 2 y 2
6
−1
250
0
10
026
19. The graph is symmetric with respect to the y-axis and consists
of waves along the t-axis, whose amplitude slowly increases
as you move farther from the origin in either direction.
Window: 30 t 30 and 6 y 6
21. The graph which is not defined at t 0, is symmetric with
respect to the y-axis and consists of waves along the t-axis
whose amplitude rapidly decreases as you move farther
from the origin in either direction.
Window: 30 t 30 and .3 y 1
23. The function is periodic with period p. (Why?) The graph
lies on or below the t-axis because the logarithmic function
is negative for numbers between 0 and 1 and cos t is
always between 0 and 1. The graph has vertical asymp-
totes when t p/2, 3p/2, 5p/2, 7p/2, . . .
(cos t 0 at these points and ln 0 is not defined).
Window: 2p t 2p and 3 y 1 (four periods).
25. (a)
(b) Maximum at t .2, t 24.4, and t 48.6, that is,
shortly after midnight. Minimum at t 17.1, t 41.3,
and t 65.5, that is, around 5:30
P.M.
(c) 24.2 hours
Section 6.6, page 502
1. Fourth quadrant 3. Second quadrant
5. Fourth quadrant
7. sin t 4/5, cos t 3/5, tan t 4/3, cot t 3/4,
sec t 5/3, csc t 5/4
9. sin t 12/13, cos t 5/13, tan t 12/5,
cot t 5/12, sec t 13/5, csc t 13/12
11. sin t 5/26, cos t 1/26, tan t 5,
cot t 1/5, sec t 26, csc t 26/5
13. sin t 3
/5
, cos t 2
/5
, tan t 3
/2
,
cot t 2
/3
, sec t 5
/2
, csc t 5
/3
15. sin t , cos t ,
tan t
1
3
2
, cot t
1
3
2
,
sec t , csc t
12
3
2
2
17. About 154.74 ft
19. (a) 0 x 150 and 5 y 20
(b) About 15.16 ft (c) About 143 ft
12 2
2
1 2
1 2
12 2
2
3
12 2
2
0
3
072
1012 ANSWERS
21. sin
4
3
p
2
3
, cos
4
3
p
1
2
, tan
4
3
p
3
,
cot
4
3
p
1
3
, sec
4
3
p
2, csc
4
3
p
2
3
23. sin
7
4
p
2
2
, cos
7
4
p
2
2
, tan
7
4
p
1,
cot
7
4
p
1, sec
7
4
p
2
, csc
7
4
p
2
25. sin
1
4
1p
2
2
, cos
1
4
1p
2
2
,
tan
1
4
1p
1, cot
1
4
1p
1,
sec
1
4
1p
2
, csc
1
4
1p
2
27. 3.8287
29. (a) 5.6511; 5.7618; 5.7731; 5.7743 (b) (sec 2)
2
31. cos t sin t 33. 1 2 sec t sec
2
t
35. cot
3
t tan
3
t 37. csc t (sec t csc t)
39. (1)(tan
2
t sec
2
t)
41. (cos
2
t 1 sec
2
t)(cos t sec t)
43. cot t 45.
2
3
t
s
a
in
n
t
t
1
1
47. 4 tan t
49. tan t
c
s
o
in
s
t
t
cos t
1
/sin t
co
1
t t
51. 1 cot
2
t 1
c
s
o
in
s
2
2
t
t
sin
2
t
si
n
2
c
t
os
2
t
si
1
n
2
t
csc
2
t
53. sec(t)
cos
1
(t)
co
1
s t
sec t
55. sin t
2
3
, cos t
1
2
, tan t 3
,
csc t
2
3
3
, sec t 2, cot t
3
3
57. sin t 1, cos t 0, tan t is undefined, cot t 0,
sec t is undefined, csc t 1
59. sin t
1
1
2
3
, cos t
1
5
3
, tan t
1
5
2
,
cot t
1
5
2
, sec t
1
5
3
, csc t
1
1
3
2
61. Possibly an identity 63. Not an identity
65. Look at the graph of y sec t in Figure 6–84 on page 501.
If you draw in the line y t, it will pass through
(p/2, p/2) and (p/2, p/2), and obviously will not
intersect the graph of y sec t when p/2 t p/2. But
it will intersect each part of the graph that lies above the
horizontal axis, to the right of t p/2; it will also intersect
those parts that lie below the horizontal axis, to the left of
p/2. The first coordinate of each of these infinitely many
intersection points will be a solution of sec t t.
67. (a)
cos u
2
sin u
(b)
tan
2
u
(c)
u
2
Chapter 6 Review, page 506
1.
p
3
3. 324° 5.
11
9
p
7. 495° 9. cos v
1
3
11. 0
13. .809 15. 3
/3 17.
2
3
19. 1.701 21.
3
3
23. 2
25. t 0 p/6 p/4 p/3 p/2
sin t 01/2 2
/2 3
/21
cos t 1 3
/2 2
/21/20
27. 9/4 29. 0 31.
2
3
33.
3
5
35.
1
1
2
3
37.
1
2
39.
2
3
41. (c) 43.
45.
3
7
47.
3
58
49. y 3
x
51.
2
3
53. 55.
3
13
57. See Figure 6–85 on page 502.
59. (d) 61.
3
2
63. 0
65. (d) 67.
1
3
69. (a)
3
2
(b) t
p
5
71.
73. Not an identity 75. Possibly an identity
77. Possibly an identity 79.
1
2
81. (a) Minimum: 8.9 hours; Maximum: 15.1 hours
(b) January 1–March 2 and October 9–December 31
83. 2 cos(5t/2)
85. f (t) 8 sin
2pt
5
28p
is one possibility.
1
0.5
−0.5
−1
−−
2π−2ππ−π
3π
22
π
3π
2 2
π
2
1
f(t) =− sin 2t
2
13
7
58
ANSWERS 1013
87. A 10.5588, b 4, c .4581
89. 0 t p/50 and 5 y 5 (one period)
91. (a)
(b)
(c) The period is 12.05 months. The graph of the func-
tion, superimposed on the data points, suggests a
good fit.
Chapter 6 Test, page 510
1.
3
p
6
2. (a)
2
3
(b)
1
2
(c) 3
3. (sin t)(sin t 1)(sin t 1) 4. About 13,888.89 radians
5. (a) (iii) (b) (i) (c) (iv)
6. (a) (b) (c)
2
3
7.
1
4
7
8. 16 sq cm
9. (a)
8
3
p
radians (b) 4.5°
10. (a)
2
53
(b)
7
53
(c)
2
7
11. 3/4
3
13
2
13
20
100
025
20
100
025
12. Linear speed: 10p inches per minute; angular speed:
2p radians per minute
13. 14.
4(3
p
3
)
15.
2
2
16.
2
3
t
s
a
in
n
t
t
1
1
17. 6.2
18. t 1/2, 3/2, 5/2, 7/2, 9/2, and 11/2
19. (a)
1
2
(b)
2
3
(c)
3
3
(d) 3
(e) 2 (f )
2
3
20. Many correct answers, including:
21. The function has period
5
p
50
(why?). So any viewing
window with the t-axis of length 6
5
p
50
2
3
7
p
5
.03427
(for instance, 0 t
2
3
7
p
5
) and 1 y 1 will show
exactly six complete waves.
−1
2
−2−442
1
x
y
−2
2
−4 −242
x
y
−1
2
−10 −8 −6 −4 −2108642
1
4
5
3
x
y
8 cos t
(sin t)(cos t sin t)
1014 ANSWERS
22. sin
3
t csc
3
t 23. 4
24. (a) f (t) 25.63 sin(.4914t 1.9451) 47.6516
(b) g(t) 24.85 sin(.5213t 2.1482) 49.1479
(c) The model in part (b) (its period is 12.05, whereas the
model in part (a) has period 12.79).
25. 1 tan
2
x 1
c
s
o
in
s
x
x
2
1
c
s
o
in
s
2
2
x
x
cos
2
x
co
s
2
x
sin
2
x
co
1
s
2
x
(by the Pythagorean Identity)
co
1
s x
2
sec
2
x
26. Definitely not an identity.
27. (a) amplitude 3, period p/2, phase shift 7/4
(b) f(t) 6 sin(pt p) or g(t) 6 cos(pt p)
28. (a)
7
13
(b) (c)
(d)
7
6
(e)
7
13
29.
1
p
2
, 2
,
5
1
p
2
, 2
,
and
3
4
p
, 2
30. A 1.6565, b 3, c 2.4270
Chapter 7
Section 7.1, page 522
1. Possibly an identity 3. Possibly an identity
5. B 7. E
9. tan x cos x
c
s
o
in
s
x
x
cos x sin x
11. cos x sec x cos x
co
1
s x
1
13. tan x csc x
c
s
o
in
s
x
x
sin
1
x
co
1
s x
sec x
15.
s
ta
e
n
c
x
x
c
s
o
in
s
x
x
co
1
s x
c
s
o
in
s
x
x
co
1
s x
sin x
17. (1 cos x)(1 cos x) 1 cos
2
x sin
2
x
19. cot x sec x sin x
c
s
o
in
s
x
x
co
1
s x
sin x
s
s
i
i
n
n
x
x
c
c
o
o
s
s
x
x
1
21. tan x cot x
c
s
o
in
s
x
x
c
s
o
in
s
x
x
c
s
o
in
s
x
x
s
s
i
i
n
n
x
x
c
c
o
o
s
s
x
x
c
s
o
in
s
x
x
si
c
n
o
2
x
s x
s
c
in
os
x
2
x
cos x
1
sin x
co
1
s x
sin
1
x
sec x csc x
23. cos x cos x sin
2
x cos x (1 sin
2
x)
cos x (cos
2
x ) cos
3
x
25. This is not an identity.
13
6
6
13
27.
c
s
o
in
s
(
(
x
x
)
)
co
si
s
n
x
x
tan x
29. cot(x)
c
s
o
in
s
(
(
x
x
)
)
co
si
s
n
x
x
cot x
31. This is not an identity.
33. sec
2
x csc
2
x (tan
2
x 1) (cot
2
x 1)
tan
2
x 1 cot
2
x 1 tan
2
x cot
2
x
35. sin
2
x(cot x 1)
2
[sin x(cot x 1)]
2
(cos x sin x)
2
cos x
1
c
s
o
in
s
x
x
2
[cos x(1 tan x)]
2
cos
2
x(tan x 1)
2
37. sin
2
x tan
2
x sin
2
x
c
s
o
in
s
2
2
x
x
sin
2
x(
c
c
o
o
s
s
2
2
x
x 1)
tan
2
x(cos
2
x 1) tan
2
x(sin
2
x) sin
2
x tan
2
x
39. (cos
2
x 1)(tan
2
x 1) (cos
2
x 1)sec
2
x
cos
2
x sec
2
x sec
2
x cos
2
x
co
1
s
2
x
sec
2
x
1 sec
2
x tan
2
x
41.
s
c
e
s
c
c
x
x
1
1
/
/
c
s
o
in
s
x
x
co
1
s x
sin
1
x
c
s
o
in
s
x
x
tan x
43. cos
4
x sin
4
x (cos
2
x)
2
(sin
2
x)
2
(cos
2
x sin
2
x)(cos
2
x sin
2
x) 1(cos
2
x sin
2
x)
cos
2
x sin
2
x
45. This is not an identity.
47. Left side:
1
sin
si
x
n x
sin
1
x
s
s
i
i
n
n
x
x
csc x 1;
Right side:
cs
c
c
o
x
t
2
x
1
c
c
s
s
c
c
2
x
x
1
1
csc x 1
Therefore,
1
sin
si
x
n x
cs
c
c
o
x
t
2
x
1
49.
s
s
e
e
c
c
x
x
t
t
a
a
n
n
x
x
1
1
s
s
i
i
n
n
x
x
51.
ta
1
n
x
co
s
s
in
x
x
c
s
o
in
s
x
x
tan x
53. By Strategy 6, we need only prove
(1 sin x) (1 sin x) cos x cos x.
Proof: (1 sin x) (1 sin x) 1 sin
2
x cos
2
x.
sin x (
c
1
o
s x
cos x)
1 cos x
sin x
co
si
s
n
x
x cos x
1 cos x
c
s
o
in
s
x
x
sin x
1 cos x
1
cos
si
x
n x
1
cos
si
x
n x
co
1
s x
c
s
o
in
s
x
x
co
1
s x
c
s
o
in
s
x
x
(csc x 1)(csc x 1)
csc x 1
sin
2
x cos
2
x sin
2
x
cos
2
x
ANSWERS 1015
55.
sec
s
2
e
x
c
2
x
1
1
s
ta
e
n
c
2
2
x
x
1
s
ta
e
n
c
2
2
x
x
sin
2
x
57.
s
c
e
s
c
c
x
x
c
s
o
in
s
x
x
1
1
/
/
c
s
o
in
s
x
x
ᎏ
c
s
o
in
s
x
x
ᎏ
tan x
c
s
o
in
s
x
x
tan x tan x 2 tan x
59.
se
1
c
x
ta
c
n
s
x
c x
1/
1
c
os
s
x
in
x/
1
c
/
o
s
s
in
x
x
co
1
s x
sin
1
x
1
c
s
o
in
s
x
x
si
s
n
in
x
x
co
c
s
os
x
x
cos x
co
s x
sin x
si
s
n
in
x
x
co
c
s
os
x
x
cos x
co
s x
sin x
sin
1
x
csc x
61.
csc x
1
sin x
1
sin
sin
x
2
x
c
s
o
in
s
2
x
x
co
1
s x
c
s
o
in
s
x
x
sec x tan x
63. This is not an identity.
65.
Conjecture: Right side cos x
Proof: 1
1
sin
c
2
o
x
s x
1
1
c
c
o
o
s
s
x
x
1
sin
c
2
o
x
s x
1
1
co
s x
co
s x
sin
2
x
co
1
s
2
x
co
c
s
o
x
s x
cos
1
x(
co
c
s
o
x
s
x
1)
cos x
67.
Conjecture: Right side tan x
Proof: (sin x cos x)(sec x csc x) cot x 2
(sin x cos x)
co
1
s x
sin
1
x
cot x 2
tan x 1 1 cot x cot x 2 tan x
−5
5
−2π 2π
cos
2
x sin
2
x cos x sin
2
x
1 cos x
−1
1
−2π 2π
1
1
sin
si
x
n
2
x
1
sin
1
x
sin x
c
s
o
in
s
2
2
x
x
cos
1
2
x
