Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

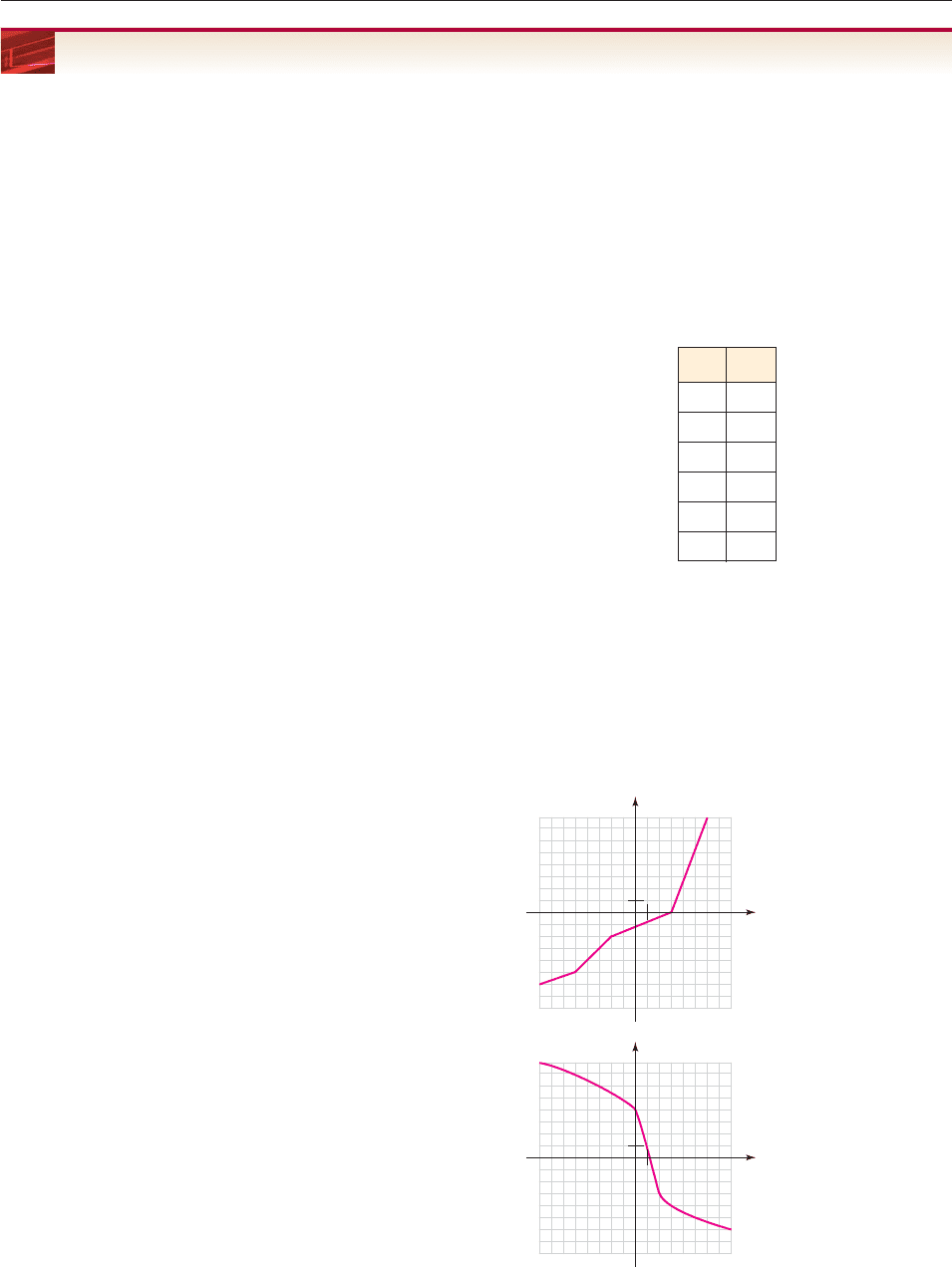
226 CHAPTER 3 Functions and Graphs
EXERCISES 3.7
In Exercises 1–8, use a calculator and the Horizontal Line Test
to determine whether or not the function f is one-to-one.
1. f (x) x
4
4x
2
3
2. f (x) x
4
4x 3
3. f (x) x
3
x 5
x 3ifx 3
4. f (x)
2x 6ifx 3
5. f (x) x
5
2x
4
x
2
4x 5
6. f (x) x
3
4x
2
x 10
7. f (x) .1x
3
.1x
2
.005x 1
8. f (x) .1x
3
.005x 1
In Exercises 9–22, use algebra to find the inverse of the given
one-to-one function.
9. f(x) x
10. f (x) x 1
11. f (x) 5x 4
12. f (x) 3x 5
13. f (x) 5 2x
3
14. f (x) (x
5
1)
3
15. f (x) 4x 7
16. f (x) 5 3x 2
17. f (x) 1/x
18. f (x) 1/x
19. f (x)
2x
1
1
20. f (x)
x
x
1
21. f (x)
x
x
3
3
1
5
22. f (x)
5
3
x
x
2
1
In Exercises 23–28, use the Round-Trip Theorem on page 223
to show that g is the inverse of f.
23. f (x) x 1, g(x) x 1
24. f (x) 2x 6, g(x)
2
x
3
25. f (x)
x
1
1
, g(x)
1
x
x
26. f (x)
2x
3
5
, g(x)
3
2
x
5x
27. f (x) x
5
, g(x)
5
x
28. f (x) x
3
1, g(x)
3
x 1
29. Show that the inverse function of the function f whose rule
is f (x)
2
3
x
x
1
2
is f itself.
30. List three different functions (other than the ones in Exam-
ple 6 and Exercise 29), each of which is its own inverse.
[Many correct answers are possible.]
31. Let f(t) be the population of rabbits on Christy’s property t
years after she received 10 of them as a gift.
Compute the following, including units, or write “not enough
information to tell.” f
1
denotes the inverse function of f.
(a) f(2) (b) f
1
(48)
(c) f
1
(71) (d) 3 f
1
(70)
(e) f
1
(2 48) (f) f(70)
(g) f
1
(4)
In Exercises 32 and 33, the graph of a function f is given. Sketch
the graph of the inverse function of f. [Reflect carefully.]
32.
33.
1
1
y
x
1
1
y
x
tf(t)
010
123
248
364
470
571
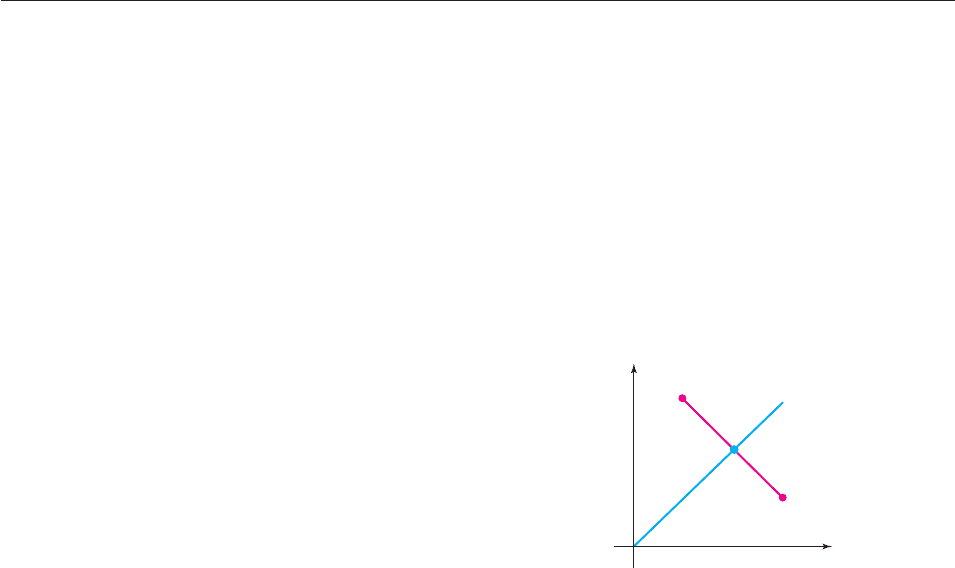
In Exercises 34–39, each given function has an inverse func-
tion. Sketch the graph of the inverse function.
34. f (x) x 3
35. f (x) 3x 2
36. f (x) .3x
5
2
37. f (x)
3
x 3
38. f (x)
5
x
3
x
2
x
2
1ifx 0
39. f (x)
.5x 1ifx 0
In Exercises 40– 42, none of the functions has an inverse. State
at least one way of restricting the domain of the function (that
is, find a function with the same rule and a smaller domain) so
that the restricted function has an inverse. Then find the rule of
the inverse function.
Example: f (x) x
2
has no inverse. But the function h with
domain all x 0 and rule h(x) x
2
is increasing (its graph is
the right half of the graph of f —see Figure 2–2 on page 78)—
and therefore has an inverse.
40. f (x) x
41. f (x) x
2
42. f (x)
4 x
2
43. f (x)
x
2
1
1
44. f (x) 3(x 5)
2
2
45. (a) Using the f
1
notation for inverse functions, find f
1
(x)
when f (x) 3x 2.
(b) Find f
1
(1) and 1/f (1). Conclude that f
1
is not the
same function as 1/f.
46. Let C be the temperature in degrees Celsius. Then the tem-
perature in degrees Fahrenheit is given by f (C)
9
5
C 32.
Let g be the function that converts degrees Fahrenheit to de-
grees Celsius. Show that g is the inverse function of f and
find the rule of g.
THINKERS
47. Let m and b be constants with m 0. Show that the func-
tion f (x) mx b has an inverse function g and find the
rule of g.
48. Prove that the function h(x) 1 .2x
3
of Example 1(c) is
one-to-one by showing that it satisfies the definition:
If a b, then h(a) h(b).
[Hint: Use the rule of h to show that when h(a) h(b), then
a b. If this is the case, then it is impossible to have
h(a) h(b) when a b.]
SECTION 3.7 Inverse Functions 227
49. Show that the points P (a, b) and Q (b, a) are symmet-
ric with respect to the line y x as follows.
(a) Find the slope of the line through P and Q.
(b) Use slopes to show that the line through P and Q is per-
pendicular to y x.
(c) Let R be the point where the line y x intersects line
segment PQ. Since R is on y x, it has coordinates
(c, c) for some number c, as shown in the figure. Use
the distance formula to show that segment PR has the
same length as segment RQ. Conclude that the line
y x is the perpendicular bisector of segment PQ.
Therefore, P and Q are symmetric with respect to the
line y x.
50. Suppose that functions f and g have these round-trip
properties:
(1) g( f (x)) x for every x in the domain of f.
(2) f (g( y)) y for every y in the domain of g.
To complete the proof of the Round-Trip Theorem, we
must show that g is the inverse function of f. Do this as
follows.
(a) Prove that f is one-to-one by showing that
if a b, then f (a) f (b).
[Hint: If f (a) f (b), apply g to both sides and use (1) to
show that a b. Consequently, if a b, it is impossi-
ble to have f (a) f (b).]
(b) If g( y) x, show that f (x)
y. [Hint: Use (2).]
(c) If f (x) y, show that g(y) x. [Hint: Use (1).]
Parts (b) and (c) prove that
g( y) x exactly when f (x) y.
Hence, g is the inverse function of f (see page 219).
51. Prove that every function f that has an inverse function g is
one-to-one. [Hint: The proof of the Round-Trip Theorem on
page 223 shows that f and g have the round-trip properties;
use Exercise 50(a).]
52. True or false: If a function has an inverse, then its inverse
has an inverse. Justify your answer.
53. True or false: If a one-to-one function is increasing, then its
inverse is increasing. Justify your answer.
(c, c)
(b, a)
(a, b)
y = x
y
P
x
R
Q

228 CHAPTER 3 Functions and Graphs
Chapter 3 Review
IMPORTANT CONCEPTS
Section 3.1
Function 144
Domain 144
Range 144
Rule 144
Greatest integer function 145
Functions defined by equations and
graphs 145
Section 3.2
Functional notation 152–153
Difference quotient 154–155
Common mistakes with functional
notation 152
Domain convention 156
Piecewise-defined functions 156–157
Section 3.3
Graphs of functions 161
Catalog of functions 162–163
Step functions 163
Graphs of piecewise-defined
functions 164
Local maximum and local minimum
165
Increasing and decreasing functions
167
Vertical Line Test 169
Graph reading 168
Special Topics 3.3.A
Parametric graphing 176–177
Section 3.4
Vertical shifts 180
Horizontal shifts 181
Expansions and contractions 182
Reflections in the x- and y-axis
184–185
Special Topics 3.4.A
Symmetry with respect to the
y-axis 189–190
Symmetry with respect to the
x-axis 190–191
Symmetry with respect to the
origin 191
Coordinate and algebraic tests for
symmetry 192
Even and odd functions 192–193
Section 3.5
Sums, differences, products, and
quotients of functions 195–196
Composition of functions
196–197
Section 3.6
Average rate of change 206
Secant lines and average rate of
change 208–209
Difference quotient 210
Estimating instantaneous rates of
change 212–213
Section 3.7
One-to-one functions 217
Horizontal Line Test 218
Inverse functions 219
Round-Trip Theorem 222
Graphs of inverse functions
224–225
IMPORTANT FACTS & FORMULAS
■
The average rate of change of a function f as x changes from a to b is the number
f (b
b
)
f
a
(a)
.
■
The average rate of change of a function f as x changes from a to b is the slope of the secant line joining
the points (a, f (a)) and (b, f (b)).
■
The difference quotient of the function f is the quantity
f (x h
h
) f (x)
.

CHAPTER 3 Review 229
CATALOG OF BASIC FUNCTIONS—PART 1
Slope = m > 0
f(x) = mx + b
x
y
Slope = m < 0
Linear Functions
Square Root Function
f(x) = mx + b
x
y
Identity Function
f(x) = x
x
y
x
y
Cube Function
Greatest Integer Function Absolute Value Function
f(x) = x
3
x
y
Square Function
f(x) = x
2
x
y
Constant Function
f(x) = b
x
y
b
f(x) = x
f(x) = ⏐x⏐
x
y
f(x) = x
x
y
1
1
1. Let x denote the greatest integer function and evaluate
(a) 5/2 . (b) 1755 .
(c) 18.7 15.7 .
(d) 7 7 .
2. If f (x) x x x, then find f(0), f (1), f (1/2), and
f(3/2).
3. Let f be the function given by the rule f (x) 7 2x. Com-
plete this table:
4. What is the domain of the function g given by
g(t)
t
t
3
2
?
5. In each case, give a specific example of a function and num-
bers a, b to show that the given statement may be false.
(a) f (a b) f (a) f (b) (b) f (ab) f (a) f (b)
6. If f (x) 3 x x 3
7, then
f (7) f (4) .
7. What is the domain of the function given by
g(r) r 4
r
2?
REVIEW QUESTIONS
x 0124 tkb 11 b 6 2u
f (x) 7
8. What is the domain of the function f (x) x
2
?
9. If h(x) x
2
3x, then h(t 2) .
10. Which of the following statements about the greatest
integer function f (x) x is true for every real num-
ber x?
(a) x x 0 (b) x x 0
(c) x x 0 (d) x x
(e) 3x 3x
11. If f (x) 2x
3
x 1, then f (x/2) .
12. If g(x) x
2
1, then g(x 1) g(x 1) .
13. The radius of an oil spill (in meters) is 50 times the square
root of the time t (in hours).
(a) Write the rule of a function f that gives the radius of the
spill at time t.
(b) Write the rule of a function g that gives the area of the
spill at time t.
(c) What are the radius and area of the spill after
9 hours?
(d) When will the spill have an area of 100,000 square
meters?
14. The cost of renting a limousine for 24 hours is given by
150 if 0 x 25
C(x)
1.75x 150 if x 25,
where x is the number of miles driven.
(a) What is the cost if the limo is driven 20 miles?
30 miles?
(b) If the cost is $218.25, how many miles were driven?
15. Sketch the graph of the function f given by
x
2
if x 0
f (x)
x 1 if 0 x 4
x
if x 4.
16. U.S. Express Mail rates in 2003 are shown in the following
table. Sketch the graph of the function e, whose rule is
e(x) cost of sending a package weighing x pounds by Ex-
press Mail.
230 CHAPTER 3 Functions and Graphs
17. Which of the following are graphs of functions of x?
(a)
(b)
18. The function whose graph is shown gives the number of
Americans who snowboard (in millions) in year x where
x 0 corresponds to 1988.*
(a) What is the domain of the function?
(b) Approximately, what is the range of the function?
(c) Find the average rate of change of the function from
x 6 to x 8 and from x 9 to x 10.
In Questions 19–22, determine the local maxima and minima of
the function, the intervals on which the function is increasing,
and the intervals on which it is decreasing.
19. g(x)
x
2
x
1
20. f (x) 2x
3
5x
2
4x 3
21. g(x) x
3
8x
2
4x 3
22. f (x) .5x
4
2x
3
6x
2
16x 2
In Questions 23 and 24, sketch the graph of the curve given by
the parametric equations.
23. x t
2
4 and y 2t 1(3 t 3)
24. x t
3
3t
2
1 and y t
2
1(3 t 2)
25. Sketch a graph that is symmetric with respect to both the
x-axis and the y-axis. (There are many correct answers and
your graph need not be the graph of an equation.)
0108
Year
12 1464
Snowboarders (in millions)
2
x
y
5
4
3
2
1
y
x
y
x
EXPRESS MAIL
Letter Rate—Post Office to
Addressee Service
Up to 8 ounces $13.65
Over 8 ounces to 2 pounds $17.85
Up to 3 pounds $21.05
Up to 4 pounds $24.20
Up to 5 pounds $27.30
Up to 6 pounds $30.40
Up to 7 pounds $33.45
*National Sporting Goods Association, TransWorld Snowboarding
Business.

26. Sketch the graph of a function that is symmetric with re-
spect to the origin. (There are many correct answers and
you don’t have to state the rule of your function.)
In Questions 27 and 28, determine algebraically whether the
graph of the given equation is symmetric with respect to the
x-axis, the y-axis, or the origin.
27. x
2
y
2
2
28. 5y 7x
2
2x
In Questions 29–31, determine whether the given function is
even, odd, or neither.
29. g(x) 9 x
2
30. f (x) xx 1
31. h(x) 3x
5
x(x
4
x
2
)
32. (a) Draw some coordinate axes and plot the points (2, 1),
(1, 3), (0, 1), (3, 2), (4, 1).
(b) Suppose the points plotted in part (a) lie on the graph of
an even function f. Plot these points: (2, f (2)), (1, f (1)),
(0, f (0)), (3, f (3)), (4, f (4)).
33. Determine whether the circle with equation
x
2
y
2
6y 5
is symmetric with respect to the x-axis, the y-axis, or the
origin.
34. Sketch the graph of a function f that satisfies all of these
conditions:
(i) domain of f [3, 4]
(ii) range of f [2, 5]
(iii) f (2) 0
(iv) f (1) 2
[Note: There are many possible correct answers and the
function whose graph you sketch need not have an algebraic
rule.]
35. Sketch the graph of g(x) 5
x
4
5
.
Use the graph of the function f in the figure to answer
Questions 36–39.
36. What is the domain of f ?
37. What is the range of f ?
38. Find all numbers x such that f (x) 1.
1
1
y
f
x
CHAPTER 3 Review 231
39. Find a number x such that f (x 1) f (x). (Many correct
answers are possible.)
Use the graph of the function f in the figure to answer Ques-
tions 40–46.
40. What is the domain of f ? 41. f (3) .
42. f (2 2) .
43. f (1) f (1) .
44. True or false: 2 f (2) f (4).
45. True or false: 3 f (2) f (4).
46. True or false: f (x) 3 for exactly one number x.
Use the graphs of the functions f and g in the figure to answer
Questions 47–52.
47. For which values of x is f (x) 0?
48. True or false: If a and b are numbers such that
5 a b 6, then g(a) g(b).
49. For which values of x is g(x) f (x)?
50. Find f (0) g(0).
51. For which values of x is f (x 1) 0?
52. What is the distance from the point (5, g(5)) to the point
(6, g(6))?
53. Fireball Bob and King Richard are two NASCAR racers.
The graph on the next page shows their distance traveled in
a recent race as a function of time.
(a) Which car made the most pit stops?
(b) Which car started out the fastest?
1
x
2 3 4 5 6
⫺
5
⫺
4
⫺
3
⫺
2
⫺
1
1
2
3
y
f
f
g
g
⫺
3
⫺
2
1
1
y
f
x
2
3
2
−2
−3
3
4 5 6
−5
−3−4 −2 −1
−1
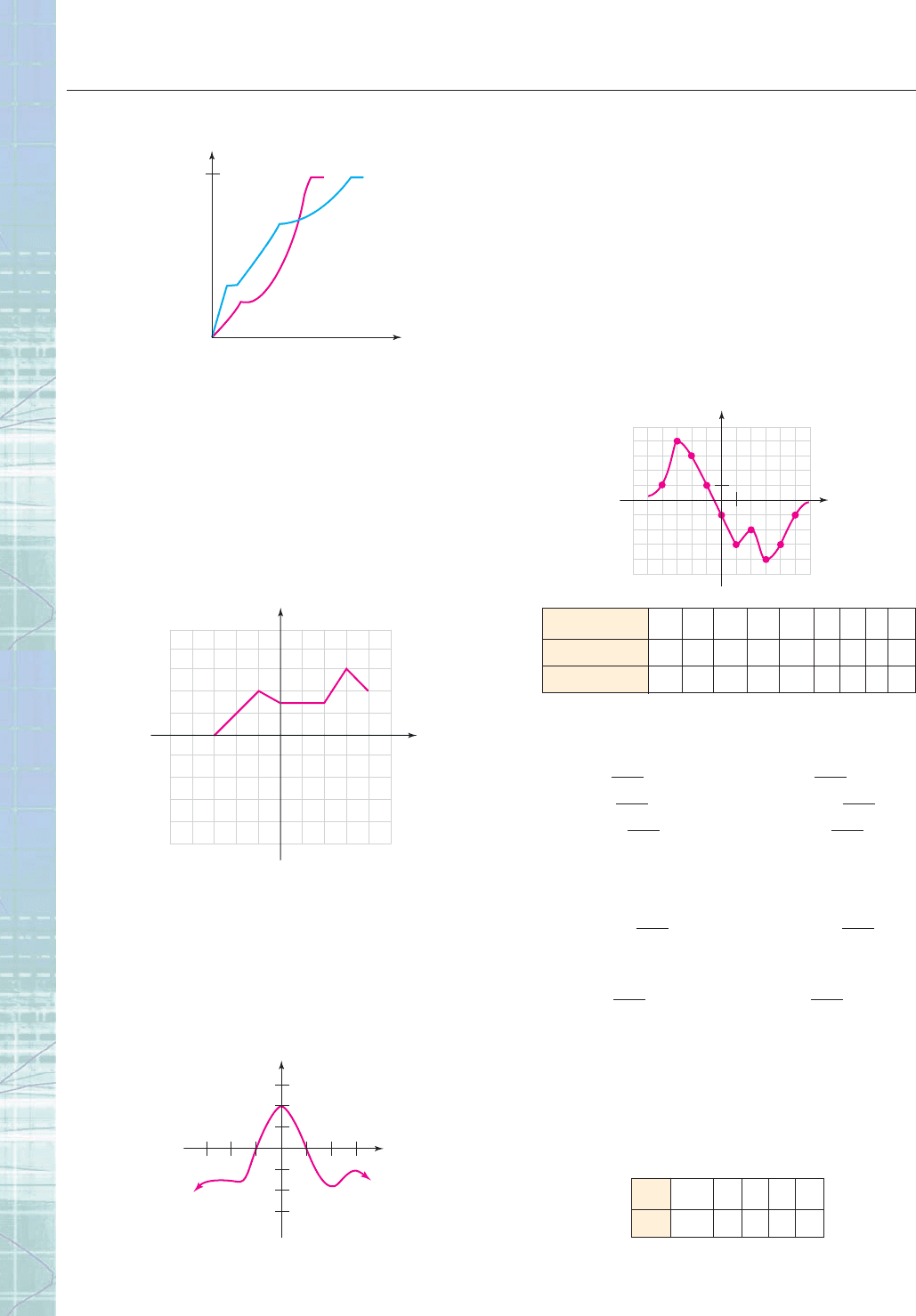
(c) Which car won the race?
In Questions 54–57, list the transformations, in the order in
which they should be performed on the graph of g(x) x
2
, so
as to produce a complete graph of the function f.
54. f (x) (x 2)
2
55. f (x) .25x
2
2
56. f (x) (x 4)
2
5 57. f (x) 3(x 7)
2
2
58. The graph of a function f is shown in the figure. On the
same coordinate plane, carefully draw the graphs of the
functions g and h whose rules are
g(x) f (x) and h(x) 1 f (x)
59. The figure shows the graph of a function f. If g is the func-
tion given by g(x) f (x 2), then which of these state-
ments about the graph of g is true?
(a) It does not cross the x-axis.
(b) It does not cross the y-axis.
(c) It crosses the y-axis at y 4.
(d) It crosses the y-axis at the origin.
(e) It crosses the x-axis at x 3.
1
x
2 3
⫺
3
⫺
2
⫺
1
2
1
3
y
⫺
3
⫺
1
⫺
2
x
y
Time
Fireball Bob
King Richard
Distance traveled
Finish line
232 CHAPTER 3 Functions and Graphs
60. If f (x) 3x 2 and g(x) x
3
1, find:
(a) ( f g)(1) (b) ( f g)(2) (c) ( fg)(0)
61. If f (x)
x
1
1
and g(x)
x
2
5
, find:
(a) ( f/g)(2) (b) (g/f )(x)
(c) ( fg)(c 1) (c 1)
62. Find two functions f and g such that neither is the identity
function, and
( f g)(x) (2x 1)
2
.
63. Use the graph of the function g in the figure to fill in the fol-
lowing table, in which h is the composite function g g.
Questions 64–69 refer to the functions f (x)
x
1
1
and g(t)
t
3
3.
64. ( f g)(1) . 65. (g f )(2) .
66. g( f (2)) . 67. (g f )(x 1) .
68. g(2 f (0)) . 69. f (g(1) 1) .
70. Let f and g be the functions given by
f (x) 4x x
4
and g(x)
x
2
1
(a) ( f g)(x) . (b) (g f )(x) .
71. If f(x)
1
x
and g(x) x
2
1, then
( f g)(x) and (g f )(x) .
72. Let f (x) x
2
. Give an example of a function g with domain
all real numbers such that g f f g.
73. If f (x)
1
1
x
and g(x) x
, then find the domain of the
composite function f g.
74. These tables show the values of the functions f and g at cer-
tain numbers:
1
y
g
x
1
x 4 3 2 10 1 234
g(x) 1
h(x) g(g(x))
x 10123
f(x) 10135
and
Which of the following statements are true?
(a) (g f )(1) 1 (b) ( f g)(2) ( f g)(0)
(c) f (1) f (2) f (3) (d) (g f )(2) 1
(e) None of the above is true.
75. Find the average rate of change of the function
g(x)
x
3
x
x
2
1
as x changes from
(a) 1 to 1 (b) 0 to 2
76. Find the average rate of change of the function
f(x)
x
2
x
1
as x changes from
(a) 3 to 0 (b) 3 to 3.5 (c) 3 to 5
77. If f (x) 2x 1 and g(x) 3x 2, find the average rate of
change of the composite function f g as x changes from 3
to 5.
78. If f (x) x
2
1 and g(x) x 2, find the average rate of
change of the composite function f g as x changes from 1
to 1.
In Questions 79–82, find the difference quotient of the function.
79. f (x) 3x 4 80. g(x) x
81. g(x) x
2
1 82. f (x) x
2
x
83. The profit (in hundreds of dollars) from selling x tons of
Wonderchem is given by
P(x) .2x
2
.5x 1.
What is the average rate of change of profit when the num-
ber of tons of Wonderchem sold increases from
(a) 4 to 8 tons? (b) 4 to 5 tons? (c) 4 to 4.1 tons?
84. On the planet Mars, the distance traveled by a falling rock
(ignoring atmospheric resistance) in t seconds is 6.1t
2
feet.
How far must a rock fall in order to have an average speed
of 25 feet per second over that time interval?
85. The graph in the figure shows the population of fruit flies
during a 50-day experiment in a controlled atmosphere.
(a) During what 5-day period is the average rate of popula-
tion growth the slowest?
400
300
200
100
Population
50403020100
Days
CHAPTER 3 Review 233
t 01234
g(t) 10125
(b) During what 10-day period is the average rate of popu-
lation growth the fastest?
(c) Find an interval beginning at the 30th day during which
the average rate of population growth is the same as the
average rate from day 10 to day 20.
86. The graph of the function g in the figure consists of straight
line segments. Find an interval over which the average rate
of change of g is
(a) 0 (b) 3(c).5
(d) Explain why the average rate of change of g is the same
from 3 to 1 as it is from 2.5 to 0.
87. The table shows the median sale price for single-family
homes in the western United States in selected years.
(a) Find the average rate of change of the median price from
1985 to 1998, from 1998 to 2001, and from 1985 to 2001.
(b) If the average rate of change from 1998 to 2001 contin-
ues in years after 2001, what is the median price in 2005?
88. Find the inverse of the function f (x) 2x 1.
89. Find the inverse of the function f (x) 5 x
7.
90. Find the inverse of the function f (x)
5
x
3
1
.
91. The graph of a function f is shown in the figure. Sketch the
graph of the inverse function of f.
x
f
y
2
2
4 6 8
−2−4
−2
x
y
Ye ar 1985 1990 1995 1998 2000 2001
Median $95,400 $129,600 $141,000 $164,800 $183,000 $194,500
Price
2
24681012
4
6810 12
2
2
4
4
6
8
x
y
Chapter
3
Test
Sections 3.1–3.3; Special Topics 3.3.A
1. Express the area of a circle as a function of its radius.
2. Consider the function f whose graph is shown below:
Label each of the following graphs with one of the labels
below, and explain your reasoning. (There are more labels
than there are graphs. Each graph gets one label, and there
will be some labels left over.)
f(x) f (x) f(3x)
f
1
3
x
f(x) 3 f (x) 3
f(x 3) f (x 3) 3 f(x)
1
3
f(x) 3f (x) f (3x)
Label:___________
22440
2
4
6
8
10
x
y
22440
2
4
6
8
10
x
y
Label:___________
Label:__________
3. The function g is given by the following graph
22440
2
4
6
8
10
x
y
22440
2
4
6
8
10
x
y
234 CHAPTER 3 Functions and Graphs
92. Which of the following functions have inverse functions
(give reasons for your answers):
(a) f (x) x
3
(b) f(x) 1 x
2
, x 0
(c) f (x) x
In Exercises 93–95, determine whether or not the given func-
tion has an inverse function (give reasons for your answer). If
it does, find the graph of the inverse function.
93. f (x) 1/x
94. f (x) .02x
3
.04x
2
.6x 4
95. f (x) .2x
3
4x
2
6x 15

CHAPTER 3 Test 235
(a) Find the domain of g (b) Find the range of g
(c) Find g(0)
4. Does the equation y x 5 define y as a function of x?
Why or why not?
5. Compute and simplify the difference quotient
f(x h
h
) f(x)
for the function f(x)
2
x
3. Assume
that h 0
6. Graph the curve given by
x t
3
t
y
3
t
with 1.5 t 1.5. Choose your viewing window carefully.
Sections 3.4–3.7; Special Topics 3.4.A
7. A child’s score, s, on a standardized test is a function of the
number of books, b, he or she has read. The formula for s is
given below:
s(b) 15 10b
100
(a) Explain in terms of books and test scores the meaning
of the following statements: s(0) 25, s
1
(35) 30.
(b) How many books would a child have to read to get a
score of 45 on the test?
8. Determine whether the given graph is symmetric with
respect to the y-axis, the x-axis, the origin, or none of these:
(a)
(b)
y
x
x
y
(c)
9. Describe a sequence of transformations that will transform
the graph of the function f into the graph of the function g
f(x) x
2
2 g(x) (x 5)
2
9
10. The height in feet of a dropped ball after t seconds is given
by h(t) 16t
2
500.
(a) Find the average rate at which the ball falls in the inter-
val from 3 to 3.1 seconds.
(b) Find the average rate at which the ball falls in the inter-
val from 3 to 3.01 seconds.
(c) Estimate the rate at which the ball falls after exactly
3 seconds.
11. The table below shows the total number of shares traded
(in millions) on the New York Stock Exchange in the
year 2007. Find the average rate of change in monthly share
volume from January through April. Include units in your
answer.
12. The given function has an inverse function. Sketch the
graph of the inverse function:
x
2
if x 0
f(x)
.6x if x 0
13. Use the round-trip theorem to show that g is the inverse
of f, where
f(x)
5
x 1
and g(x) x
5
1
x
y
Month January February March April
Volume 110.15 106.07 139.35 108.24
