Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

The remainder Theorem shows that the remainder when f (x) is divided by
x 3 is the number f (3), which is 0, as we saw in part (a). Therefore,
f (x) (x 3)q(x) 0 (x 3)q(x).
Thus, x 3 is a factor of f (x). [To determine the other factor, the quotient
q(x), you have to perform the division.] ■
Example 7 illustrates this fact, which can be proved by the same argument used
in the example.
256 CHAPTER 4 Polynomial and Rational Functions
Factor
Theorem
The number c is a root of the polynomial f (x) exactly when x c is a factor
of f (x).
EXAMPLE 8
The graph of f (x) 15x
3
x
2
114x 72 in the standard viewing window
(Figure 4–8) is obviously not complete but suggests that 3 is an x-intercept, and
hence a root of f (x). It is easy to verify that this is indeed the case.
f (3) 15(3)
3
(3)
2
114(3) 72 405 9 342 72 0.
Since 3 is a root, x (3) x 3 is a factor of f (x). Use synthetic or long
division to verify that the other factor is 15x
2
46x 24. By factoring this
quadratic, we obtain a complete factorization of f (x).
f (x) (x 3)(15x
2
46x 24) (x 3)(3x 2)(5x 12). ■
EXAMPLE 9
Find three polynomials of different degrees that have 1, 2, 3, and 5 as roots.
SOLUTION A polynomial that has 1, 2, 3, and 5 as roots must have x 1,
x 2, x 3, and x (5) x 5 as factors. Many polynomials satisfy these
conditions, such as
g(x) (x 1)(x 2)(x 3)(x 5) x
4
x
3
19x
2
49x 30
h(x) 8(x 1)(x 2)(x 3)
2
(x 5)
k(x) 2(x 4)
2
(x 1)(x 2)(x 3)(x 5)(x
2
x 1).
Note that g has degree 4. When h is multiplied out, its leading term is 8x
5
, so h has
degree 5. Similarly, k has degree 8 since its leading term is 2x
8
. ■
If a polynomial f (x) has four roots, say a, b, c, d, then by the same argument
used in Example 8, it must have
(x a)(x b)(x c)(x d)
as a factor. Since (x a)(x b)(x c)(x d ) has degree 4 (multiply it out—its
leading term is x
4
), f (x) must have degree at least 4. In particular, this means that
10
10
−10
−10
Figure 4–8

SECTION 4.2 Polynomial Functions 257
Number
of Roots
A polynomial of degree n has at most n distinct roots.
EXERCISES 4.2
In Exercises 1–10, determine whether the given algebraic
expression is a polynomial. If it is, list its leading coefficient,
constant term, and degree.
1. 1 x
3
2. 7 3. (x 1)(x
2
1)
4. 7
x
2x 1 5. (x 3
)(x 3
)
6. x
3
3x
2
p
3
7. x
3
3x
2
p
x
8. 4x
2
3 x
5 9.
x
7
2
5
x
15
10. (x 1)
k
(where k is a fixed positive integer)
In Exercises 11–18, state the quotient and remainder when the
first polynomial is divided by the second. Check your division
by calculating (Divisor)(Quotient) Remainder.
11. 3x
4
8x
2
6x 1; x 1
12. x
5
x
3
x 5; x 2
13. x
5
2x
4
6x
3
x
2
5x 1; x
3
1
14. 2x
5
5x
4
x
3
7x
2
13x 12; x
2
2x 3
15. 2x
5
5x
4
x
3
7x
2
13x 12; 2x
3
x
2
7x 4
16. 3x
4
3x
3
11x
2
6x 1; x
3
x
2
2
17. 5x
4
5x
2
5; x
2
x 1
18. x
5
1; x 1
In Exercises 19–22, determine whether the first polynomial is a
factor of the second.
19. x
2
5x 1; x
3
2x
2
5x 6
20. x
2
9; 4x
5
13x
4
36x
3
108x
2
81
21. x
2
3x 1; x
4
3x
3
2x
2
3x 1
22. x
2
4x 7; x
3
3x
2
3x 9
In Exercises 23–27, determine which of the given numbers are
roots of the given polynomial.
23. 2, 3, 5, 1; g(x) x
4
6x
3
x
2
30x
24. 1, 1/2, 2, 1/2, 1/3; f (x) 6x
2
x 1
25. 2 2
, 2
, 2
, 1, 1; h(x) x
3
x
2
8x 8
26. 3
, 3
, 1, 1; k(x) 8x
3
12x
2
6x 9
27. 3, 3, 0; l(x) x(x 3)
27
In Exercises 28–38, find the remainder when f (x) is divided by
g(x), without using division.
28. f (x) x
2
1; g(x) x 1
29. f (x) x
10
x
8
; g(x) x 1
30. f (x) x
6
10; g(x) x 2
31. f (x) 3x
4
6x
3
2x 1; g(x) x 3/2
32. f (x) x
5
3x
2
2x 1; g(x) x 3
33. f (x) x
3
2x
2
8x 4; g(x) x 2
34. f (x) 10x
70
8x
60
6x
40
4x
32
2x
15
5;
g(x) x 1
35. f (x) 2x
5
3
x
4
x
3
3
x
2
3
x 100;
g(x) x 10
36. f (x) x
3
8x
2
29x 44; g(x) x 11
37. f (x) 2px
5
3px
4
2px
3
8px 8p;
g(x) x 20
38. f (x) x
5
10x
4
20x
3
5x 95; g(x) x 10
In Exercises 39–46, use the Factor Theorem to determine
whether or not h(x) is a factor of f (x).
39. h(x) x 1; f (x) x
5
1
40. h(x) x 1/2; f (x) 2x
4
x
3
x 3/4
41. h(x) x 3; f (x) x
3
3x
2
4x 12
42. h(x) x 1; f (x) x
3
4x
2
3x 8
43. h(x) x 1; f (x) 14x
99
65x
56
51
44. h(x) x 2; f (x) x
3
x
2
4x 4
45. h(x) x 2
; f (x) 3x
3
4x
2
6x 8
46. h(x) x 2; f (x) x
3
2
x
2
(6 2
)x 62
no polynomial of degree 3 can have four or more roots. A similar argument works
in the general case.
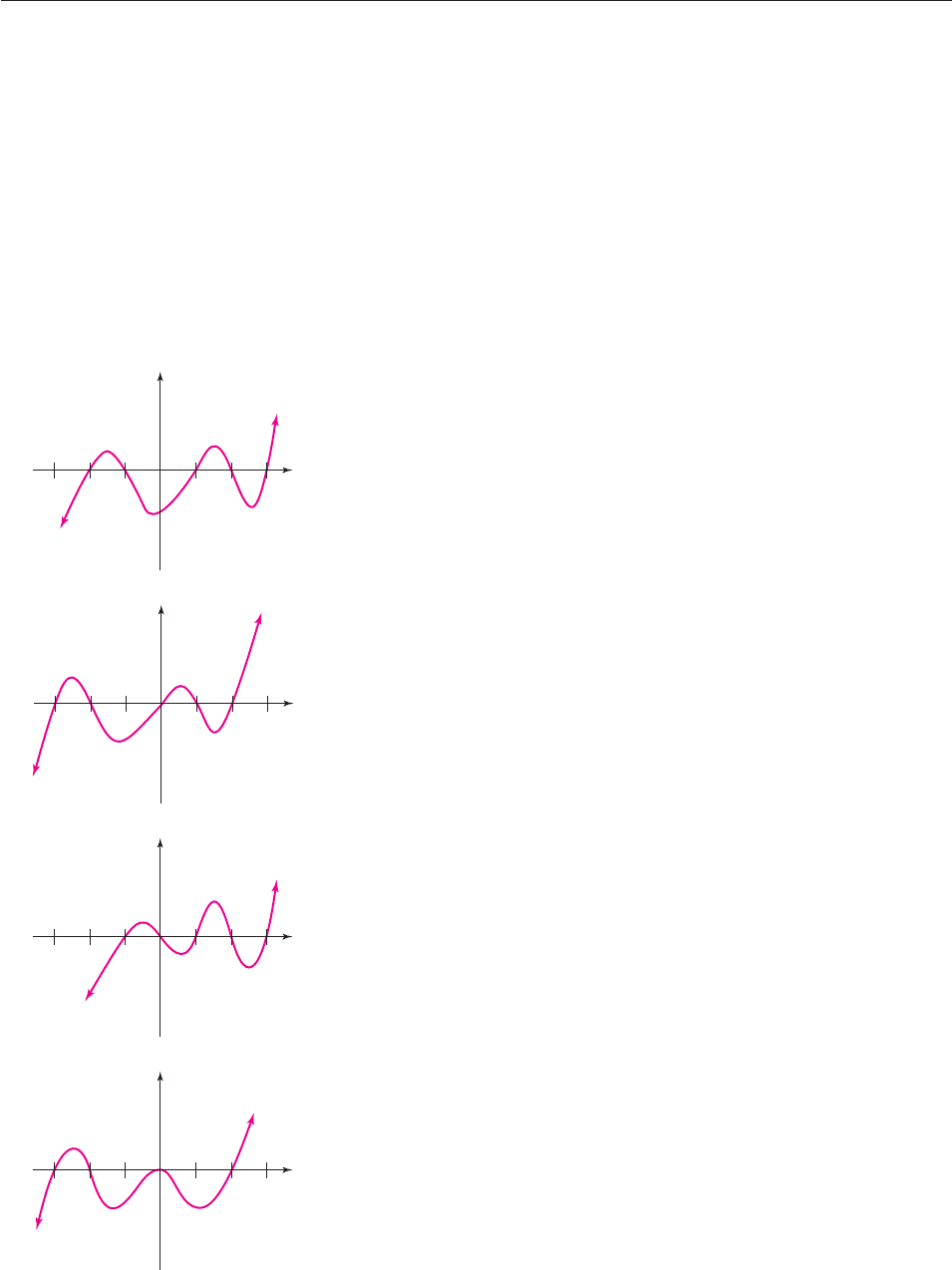
In Exercises 47–50, use the Factor Theorem and a calculator
to factor the polynomial, as in Example 7.
47. f (x) 6x
3
7x
2
89x 140
48. g(x) x
3
5x
2
5x 6
49. h(x) 4x
4
4x
3
35x
2
36x 9
50. f (x) x
5
5x
4
5x
3
25x
2
6x 30
In Exercises 51–54, each graph is of a polynomial function f(x)
of degree 5 whose leading coefficient is 1. The graph is not
drawn to scale. Use the Factor Theorem to find the polynomial.
[Hint: What are the roots of f(x)? What does the Factor
Theorem tell you?]
51.
52.
53.
54.
x
y
−3 −2 −1123
x
y
−3 −2 −1123
x
y
−3 −2 −1123
x
y
−3 −2 −1123
In Exercises 55–60, find a polynomial with the given degree n,
the given roots, and no other roots.
55. n 3; roots 1, 7, 4
56. n 3; roots 1, 1
57. n 2; roots 1, 1
58. n 1; root 5
59. n 6; roots 1, 2, p
60. n 5; root 3
61. Find a polynomial function f of degree 3 such that
f (10) 25
and the roots of f (x) are 0, 5, and 8.
62. Find a polynomial function g of degree 4 such that the roots
of g are 0, 1, 2, 3, and g(3) 288.
In Exercises 63–66, find a number k satisfying the given
condition.
63. x 2 is a factor of x
3
3x
2
kx 2.
64. x 3 is a factor of x
4
5x
3
kx
2
18x 18.
65. x 1 is a factor of k
2
x
4
2kx
2
1.
66. x 2 is a factor of x
3
kx
2
3x 7k.
67. Use the Factor Theorem to show that for every real number
c, x c is not a factor of x
4
x
2
1.
68. Let c be a real number and n a positive integer.
(a) Show that x c is a factor of x
n
c
n
.
(b) If n is even, show that x c is a factor of x
n
c
n
.
[Remember: x c x (c).]
69. (a) If c is a real number and n an odd positive integer, give
an example to show that x c may not be a factor of
x
n
c
n
.
(b) If c and n are as in part (a), show that x c is a factor
of x
n
c
n
.
THINKERS
70. For what value of k is the difference quotient of
g(x) kx
2
2x 1
equal to 7x 2 3.5h?
71. For what value of k is the difference quotient of
f (x) x
2
kx
equal to 2x 5 h?
72. Use the fact that x 2 is a factor of x
3
6x
2
9x 2 to
find all the roots of
f (x) x
3
6x
2
9x 2.
73. Use the fact that (x 3)
2
is a factor of x
4
2x
3
91x
2
492x 684 to find all the roots of
f (x) x
4
2x
3
91x
2
492x 684.
258 CHAPTER 4 Polynomial and Rational Functions

■ Use synthetic division to divide a polynomial by a polynomial of
the form x c.
■ Find factors of a polynomial using synthetic division.
Synthetic division is a fast method of doing polynomial division when the divisor
is a first-degree polynomial of the form x c for some real number c. To see how
it works, we first consider an example of ordinary long division.
SPECIAL TOPICS 4.2.A Synthetic Division 259
4.2.A SPECIAL TOPICS Synthetic Division
Section Objectives
3x
3
6x
2
4x 3 Quotient
Divisor
x 23x
4
8x
2
11x 1 Dividend
3x
4
6x
3
6x
3
8x
2
6x
3
12x
2
4x
2
11x
4x
2
8x
3x 1
3x 6
5 Remainder
This calculation involves a lot of redundancy. If we insert 0 coefficients for
terms that don’t appear above and keep the various coefficients in the proper
columns, we can eliminate the repetition and all the x’s.
36 4 3
Quotient
Divisor 1 23 0 8 11 1 Dividend
6
6
12
4
8
3
6
5 Remainder
We can make our work cleaner by moving the lower lines upward and writing 2
in the divisor position (since that’s enough to remind us that the divisor is x 2).
36 43
Quotient
Divisor 23 0 8 11 1 Dividend
6 12 86
643 5
Remainder
Since the last line contains most of the quotient line, we can save more space and
still preserve the essential information by inserting a 3 in the last line and omitting
the top line.
Synthetic division is a quick method for obtaining the last row of this array.
Here is a step-by-step explanation of the division of 3x
4
8x
2
11x 1 by
x 2.
Step 1 In the first row, list the 2
from the divisor and the coeffi-
cients of the dividend in order
of decreasing powers of x
(insert 0 coefficients for
missing powers of x).
Step 2 Bring down the first
dividend coefficient (namely, 3)
to the third row
Step 3 Multiply 2
3 and insert
the answer 6 in the sec-
ond row, in the position
shown here.
Step 4 Add 0 6 and write the
answer 6 in the third
row.
Step 5 Multiply 2
6 and insert
the answer 12 in the second
row.
Step 6 Add 8 12 and write
the answer 4 in the third
row.
Step 7 Multiply 2
4 and insert
the answer 8 in the sec-
ond row.
Step 8 Add 11 8 and write
the answer 3 in the
third row.
Step 9 Multiply 2
(3) and
insert the answer 6
in the second row.
Step 10 Add 1 (6) and
write the answer 5
in the third row.
260 CHAPTER 4 Polynomial and Rational Functions
Divisor 23 0 8 11 1 Dividend
6 12 86
36 43 5 Remainder
1444424443
Quotient
2308 11 1
23
3
0 8 11 1
23
3
0
6
8 11 1
23
3
0
6
6
8 11 1
23
3
0
6
6
8
12
11 1
23
3
0
6
6
8
12
4
11 1
23
3
0
6
6
8
12
4
11
8
1
23
3
0
6
6
8
12
4
11
3
8
1
23
3
0
6
6
8
12
4
11
3
8
1
6
23
3
0
6
6
8
12
4
11
3
8
1
6
5
Except for the signs in the second row, this last array is the same as the array
obtained from the long division process, and we can read off the quotient and
remainder:
The last number in the third row is the remainder.
The other numbers in the third row are the coefficients of the quotient
(arranged in order of decreasing powers of x).
Since we are dividing the fourth-degree polynomial 3x
4
8x
2
11x 1 by the
first-degree polynomial x 2, the quotient must be a polynomial of degree three
with coefficients 3, 6, 4, 3, namely, 3x
3
6x
2
4x 3. The remainder is 5.
SPECIAL TOPICS 4.2.A Synthetic Division 261
CAUTION
Synthetic division can be used only when the divisor is a first-degree polynomial of the form
x c. In the example above, c 2. If you want to use synthetic, division with a divisor such as
x 3, you must write it as x (3), which is of the form x c with c 3.
EXAMPLE 1
To divide x
5
5x
4
6x
3
x
2
4x 29 by x 3, we write the divisor as
x (3) and proceed as above.
31561429
3 60321
12017 8
The last row shows that the quotient is x
4
2x
3
x 7 and the remainder
is 8. ■
EXAMPLE 2
Show that x 7 is a factor of 8x
5
52x
4
2x
3
198x
2
86x 14 and find
the other factor.
SOLUTION x 7 is a factor exactly when division by x 7 leaves remainder
0, in which case the quotient is the other factor. Using synthetic division, we have
7852 2 198 86 14
56 28 210 84 14
84301220
Since the remainder is 0, the divisor x 7 and the quotient
8x
4
4x
3
30x
2
12x 2
are factors.
8x
5
52x
4
2x
3
198x
2
86x 14
(x 7)(8x
4
4x
3
30x
2
12x 2). ■
TECHNOLOGY TIP
Synthetic division programs are in the
Program Appendix.

262 CHAPTER 4 Polynomial and Rational Functions
EXERCISES 4.2.A
In Exercises 1–8, use synthetic division to find the quotient and
remainder.
1. (3x
4
8x
3
9x 8) (x 2)
2. (4x
3
3x
2
6x 7) (x 2)
3. (2x
4
7x
3
2x 8) (x 3)
4. (3x
3
2x
2
8) (x 5)
5. (5x
4
3x
2
4x 6) (x 7)
6. (3x
4
2x
3
7x 4) (x 3)
7. (x
6
1) (x 1)
8. (x
6
x
5
x
4
x
3
x
2
x 1) (x 3)
In Exercises 9–12, use synthetic division to find the quotient
and the remainder. In each divisor x c, the number c is not
an integer, but the same technique will work.
9. (3x
4
2x
2
2)
x
1
4
10. (2x
4
3x
2
1)
x
1
2
11. (x
3
x
2
2x 2) (x 2
)
12.
10x
5
3x
4
14x
3
13x
2
4
3
x
7
3
x
1
5
In Exercises 13–16, use synthetic division to show that the first
polynomial is a factor of the second and find the other factor.
13. x 4; x
3
3x
2
34x 120
14. x 5; x
5
8x
4
17x
2
293x 15
15. x 1/2; 2x
5
7x
4
15x
3
6x
2
10x 5
16. x 1/3; 3x
6
x
5
6x
4
7x
3
3x
2
15x 5
In Exercises 17 and 18, use a calculator and synthetic division
to find the quotient and remainder.
17. (x
3
5.27x
2
10.708x 10.23) (x 3.12)
18. (2.79x
4
4.8325x
3
6.73865x
2
.9255x 8.125)
(x 1.35)
19. When x
3
cx 4 is divided by x 2, the remainder is 4.
Find c.
20. If x d is a factor of 2x
3
dx
2
(1 d
2
)x 5, what
is d?
THINKERS
21. Let g(x) x
5
2x
4
x
3
3x 1.
(a) Show that when we use synthetic division to divide by
(x 3), the quotient’s coefficients are all positive.
(b) Show that when we divide by (x a), where a 3, the
quotient’s coefficients are all positive.
(c) Use part (b) to show that g has no root greater than
three.
22. Let g(x) be a polynomial function. Assume that dividing g
by x a gives a quotient with all positive terms and a pos-
itive remainder. What does this tell us about the possible
roots of g(x)?
4.3 Real Roots of Polynomials
■ Use the Rational Root Test to find the rational roots of a
polynomial.
■ Use the Bounds Test and a graphing calculator to find
an interval that contains all the real roots of a
polynomial.
Finding the real roots of polynomials is the same as solving polynomial equations.
The root of a first-degree polynomial, such as 5x 3, can be found by solving the
equation 5x 3 0. Similarly, the roots of any second-degree polynomial can be
found by using the quadratic formula (Section 1.2). Although the roots of higher-
degree polynomials can always be approximated graphically as in Section 2.2, it
is better to find exact solutions, if possible.
Section Objectives
RATIONAL ROOTS
When a polynomial has integer coefficients, all of its rational roots (roots that are
rational numbers) can be found exactly by using the following result.
SECTION 4.3 Real Roots of Polynomials 263
The Rational
Root Test
If a rational number r/s (in lowest terms) is a root of the polynomial
a
n
x
n
a
1
x a
0
,
where the coefficients a
n
, . . . , a
1
, a
0
are integers with a
n
0, a
0
0, then
r is a factor of the constant term a
0
and
s is a factor of the leading coefficient a
n
.
The test states that every rational root must satisfy certain conditions.* By finding
all the numbers that satisfy these conditions, we produce a list of possible rational
roots. Then we must evaluate the polynomial at each number on the list to see
whether the number actually is a root. This testing process can be considerably
shortened by using a calculator, as in the next example.
EXAMPLE 1
Find the rational roots of
f (x) 2x
4
x
3
17x
2
4x 6.
SOLUTION If f (x) has a rational root r/s, then by the Rational Root Test r
must be a factor of the constant term 6. Therefore, r must be one of 1, 2, 3,
or 6 (the only factors of 6). Similarly, s must be a factor of the leading coeffi-
cient 2, so s must be one of 1 or 2 (the only factors of 2). Consequently, the
only possibilities for r/s are
1
1
,
2
1
,
3
1
,
6
1
,
1
2
,
2
2
,
3
2
,
6
2
.
Eliminating duplications from this list, we see that the only possible rational
roots are
1, 1, 2, 2, 3, 3, 6, 6,
1
2
,
1
2
,
3
2
,
3
2
.
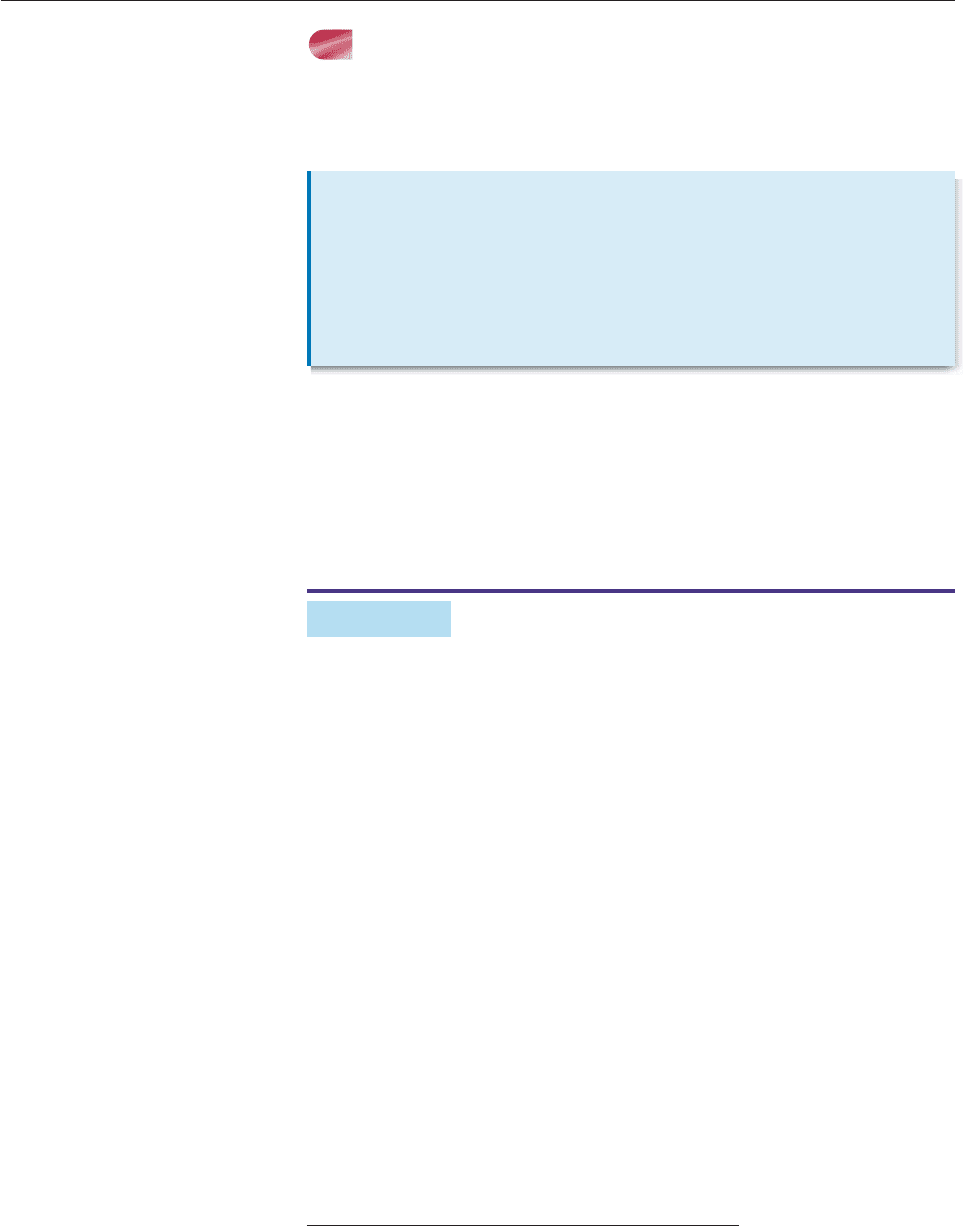
Now graph f (x) in a viewing window that includes all of these numbers on the
x-axis, say 7 x 7 and 5 y 5 (Figure 4–9 on the next page). A com-
plete graph isn’t necessary, since we are interested only in the x-intercepts.
*Since the proof of the Rational Root Test sheds no light on how the test is actually used to solve
equations, it will be omitted.
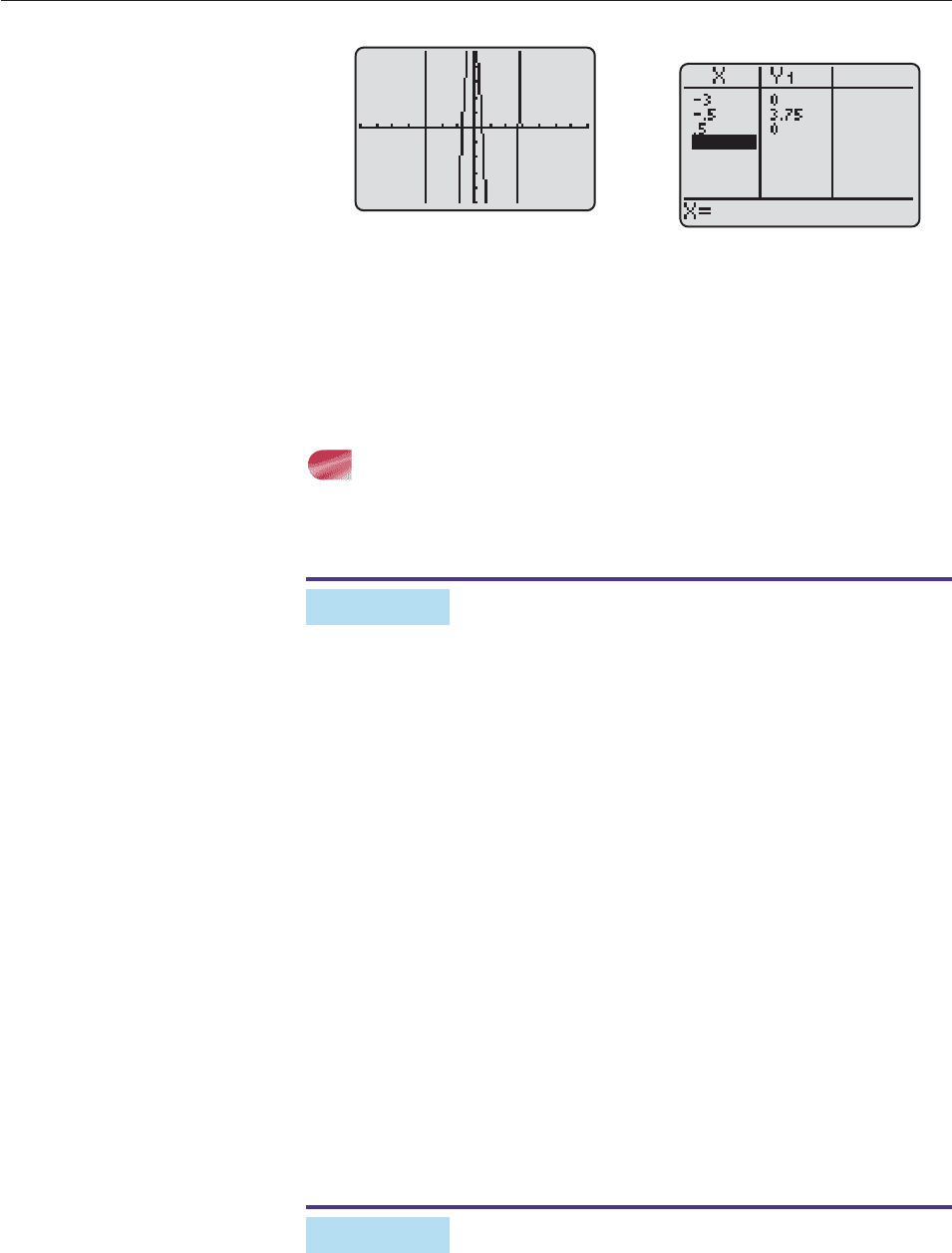
Figure 4–9 shows that the only numbers on our list that could possibly be roots
(x-intercepts) are 3, 1/2, and 1/2, so these are the only ones that need be
tested. We use the table feature to evaluate f (x) at these three numbers (Fig-
ure 4–10). The table shows that 3 and 1/2 are the only rational roots of f (x). Its
other roots (x-intercepts) in Figure 4–9 must be irrational numbers. ■
ROOTS AND THE FACTOR THEOREM
Once some roots of a polynomial have been found, the Factor Theorem can be
used to factor the polynomial, which may lead to additional roots.
EXAMPLE 2
Find all the roots of f (x) 2x
4
x
3
17x
2
4x 6.
SOLUTION In Example 1, we saw that 3 and 1/2 are the rational roots of
f (x). By the Factor Theorem, x (3) x 3 and x 1/2 are factors of f (x).
Using synthetic or long division twice, we have
2x
4
x
3
17x
2
4x 6 (x 3)(2x
3
5x
2
2x 2)
(x 3)(x .5)(2x
2
4x 4).
The remaining roots of f (x) are the roots of 2x
2
4x 4, that is, the solutions of
2x
2
4x 4 0
x
2
2x 2 0.
They are easily found by the quadratic formula.
x
2
2
12
2
2
2 3
1 3
.
Therefore, f (x) has rational roots 3 and 1/2, and irrational roots 1 3
and
1 3
. ■
EXAMPLE 3
Factor f (x) 2x
5
10x
4
7x
3
13x
2
3x 9 completely.
(2)
(2)
2
4
1
(
2)
2 1
264 CHAPTER 4 Polynomial and Rational Functions
5
7
−7
−5
Figure 4–9
Figure 4–10

SOLUTION We begin by finding as many roots of f (x) as we can. By the
Rational Root Test, every rational root is of the form r/s where r 1, 3, or
9 and s 1 or 2. Thus, the possible rational roots are
1, 3, 9,
1
2
,
3
2
,
9
2
.
The partial graph of f (x) in Figure 4–11 shows that the only possible roots
(x-intercepts) are 1 and 3. You can easily verify that both 1 and 3 are roots of f (x).
Since 1 and 3 are roots, x (1) x 1 and x 3 are factors of f (x) by
the Factor Theorem. Division shows that
f (x) 2x
5
10x
4
7x
3
13x
2
3x 9
(x 1)(2x
4
12x
3
19x
2
3x 9)
(x 1)(x 3)(2x
3
6x
2
x 3).
The other roots of f (x) are the roots of g(x) 2x
3
6x
2
x 3. We first check for
rational roots of g(x). Since every root of g(x) is also a root of f (x) (why?), the only
possible rational roots of g(x) are 1 and 3 [the rational roots of f (x)]. We have
g(1) 2(1)
3
6(1)
2
(1) 3 12;
g(3) 2(3
3
) 6(3
2
) 3 3 0.
So 1 is not a root, but 3 is a root of g(x). By the Factor Theorem, x 3 is a fac-
tor of g(x). Division shows that
f (x) (x 1)(x 3)(2x
3
6x
2
x 3)
(x 1)(x 3)(x 3)(2x
2
1).
Since 2x
2
1 has no real roots, it cannot be factored. So the factorization of f (x)
is complete. ■
BOUNDS
The polynomial f (x) in Example 2 had degree 4 and had four real roots. Since a
polynomial of degree n has at most n roots, we know that we found all the roots
of f (x). In other cases, however, special techniques may be needed to guarantee
that we have found all the roots.
EXAMPLE 4
Prove that all the real roots of
g(x) x
5
2x
4
x
3
3x 1
lie between 1 and 3. Then find all the real roots of g(x).
SOLUTION We first prove that g(x) has no root larger than 3, as follows. Use
synthetic division to divide g(x) by x 3.*
312 1031
3361863
1 1 2 6 21 64
Thus, the quotient is x
4
x
3
2x
2
6x 21, and the remainder is 64. Apply-
ing the Division Algorithm, we have
f (x) (x 3)(x
4
x
3
2x
2
6x 21) 64.
SECTION 4.3 Real Roots of Polynomials 265
10
10
−10
−10
Figure 4–11
*If you haven’t read Special Topics 4.2.A, use long division to find the quotient and remainder.
