James I.N. Introduction to Circulating Atmospheres

Подождите немного. Документ загружается.

5.4

Theories

baroclinic instability

149

vertical derivatives which appear in the quasi-geostrophic equations are

represented by finite difference formulae. One advantage of this system is

that it is straightforward to retain the /J-effect in the vorticity equation,

and also to add in such effects as friction. Such flexibility has led the

two-layer system to be called a 'white mouse' model; that is, it is simple

and expendable but can be used for a variety of experiments which would

not be possible with a more elaborate system! The disadvantage is that the

extreme simplification of the vertical structure can give misleading results, for

example by predicting stability when a more elaborate model would show

instability of very shallow disturbances. A dispersion relation is derived

from the linearized vorticity and thermodynamic equations for the system;

the boundary conditions on the vertical velocity are incorporated through

the finite difference representation of the stretching terms in the vorticity

equation and the vertical advection term in the thermodynamic equation.

The growth rate for wavelike disturbances, including /? but excluding friction,

is:

(5 59)

Figure 5.23 shows some plots of growth rate versus wavenumber for various

values of

/?.

Like the Eady model, this growth rate has a short wave

cutoff.

When K

—•

0, there is also a long wave

cutoff.

The effect of

is to reduce

the growth rates. For /? = 0, the maximum growth rate and the short wave

cutoff are at similar, but not identical, wavenumbers as in the Eady model;

the maximum growth rate is also similar. The dynamics of the two-layer

system can be interpreted in terms of two interacting waves, one confined to

the upper layer and one to the lower layer. Instability occurs when they can

phase lock, with a westward tilt with height.

The final model that will be mentioned is Charney's model. In fact, this

was the first model of baroclinic instability to be published. It is based

on a configuration which is very similar to that of the Eady model. The

two differences are that the upper boundary is removed to infinity, and that

the /? term is retained in the vorticity equation. These apparently simple

modifications lead to considerable complications in the mathematics. The

actual results, in terms of the growth rates and structures of the normal

modes, are similar to the results from the two-level system or from the

Eady model. In the Charney model, unstable modes have a large amplitude

and temperature flux, etc., below a certain height which depends upon the

wavelength of the mode. Above this level they die away. The phase speed is

nonzero, and is equal to the flow speed at a given level, called the 'steering

150

Transient disturbances

the midlatitudes

level

variables

pressure

1 —

2 —

u,v

3 u,v

4 p

Fig. 5.22. The configuration of the two-layer model of baroclinic instability.

1.0

Zonal wavenumber

2.0

Fig. 5.23. Growth rate versus wavenumber for the two-level model for various

values of jS, calculated from Eq. (5.59). Growth rates are scaled by K

AU and

wavenumbers by K

. Basic parameters are for a /?-plane centred at 45° with

= 10~

and a vertical shear of

ms"

roughly corresponding to northern

hemisphere winter. Solid curve: j8 = 0. Dashed curve: /? = 8.1 x lO'^m^s"

Dotted curve: p = 1.6 x 10~

5.4

Theories

baroclinic instability

151

level',

the atmosphere. The steering level

also the level above which

the mode dies away. Mathematically, the steering level acts

as a

critical

level for the system (see Chapter 6), which reflects vertically propagating

wave activity.

the case

the unstable modes, they are 'over reflected',

that is, they gain energy from the reflection

the critical level. There is

short wave and

long wave

cutoff,

and the scale and growth rate

the

most unstable mode are similar to those of the most unstable Eady wave.

For typical midlatitude values of the various parameters, the steering level

is around

70 kPa,

and the wavelength of the most unstable mode is around

4000

km.

Once again, the source of the instability may be envisaged as an

interaction between two wave trains. One is similar to the boundary wave

of the Eady model with the upper boundary removed to infinity. The other

Rossby wave which can propagate as

result of the potential vorticity

gradient in the fluid interior.

All the models described

this section succeed

representing,

in a

qualitative way, the distribution of temperature flux, and hence the primary

eddy generating energy conversions, actually observed

the atmosphere.

However, none

them

any way represents the observed momentum

fluxes. Indeed,

cursory examination of the solutions for the Eady model

reveals that there are no horizontal phase tilts

the wave and hence no

momentum fluxes. The same is true of the two-level and Charney models. In

order to generate unstable modes with horizontal phase tilts, it is necessary to

introduce

basic flow U

U(y

z').

This apparently trivial generalization in

fact leads to insuperable mathematical difficulties and no general analytical

solutions are known. The problem

that the linearized equations are no

longer separable, that is, the normal modes cannot be represented by some

function

\p*

Aiz^Biy^-^K

(5.60a)

as for the Eady model and the other models discussed above, but rather by

\p*

=A(y,z')e

i{kx

(Ot)

(5.60b)

The amplitude A(y, z

) must be determined by approximate numerical means

for any particular

U(y,z').

Although no general solutions

this problem

are known, some general necessary conditions for instability can be derived

on energetics grounds. These are related to the conditions needed for phase

locking two wavetrains together, and are expressed in terms of the boundary

temperature gradients

and Gu and the interior potential vorticity gradient

152 Transient disturbances in the midlatitudes

[q]y-

[<?]>>

—

~Q~2

TZJ

I 775^7 I

(5.61)

These necessary conditions may be summarized:

(i) [q]

must change sign in the y-z

plane,

(ii) —[4\y

d GL must have opposite signs,

(iii) — [q]

and

—GJJ

must have opposite signs,

(iv) G

and —

GJJ

must have opposite signs.

Condition (ii) applies to the Charney model and condition (iv) applies to the

Eady model. Note that these are necessary but not sufficient conditions for

instability. The introduction of extra effects such as friction can have an

important effect in modifying (sometimes unexpectedly) the instability of the

flow. Rather broad bounds on the growth rate and phase speeds of unstable

disturbances can be derived. But more specific information about the actual

growth rate or structure of the unstable modes in this more general case can

only be obtained by numerical means.

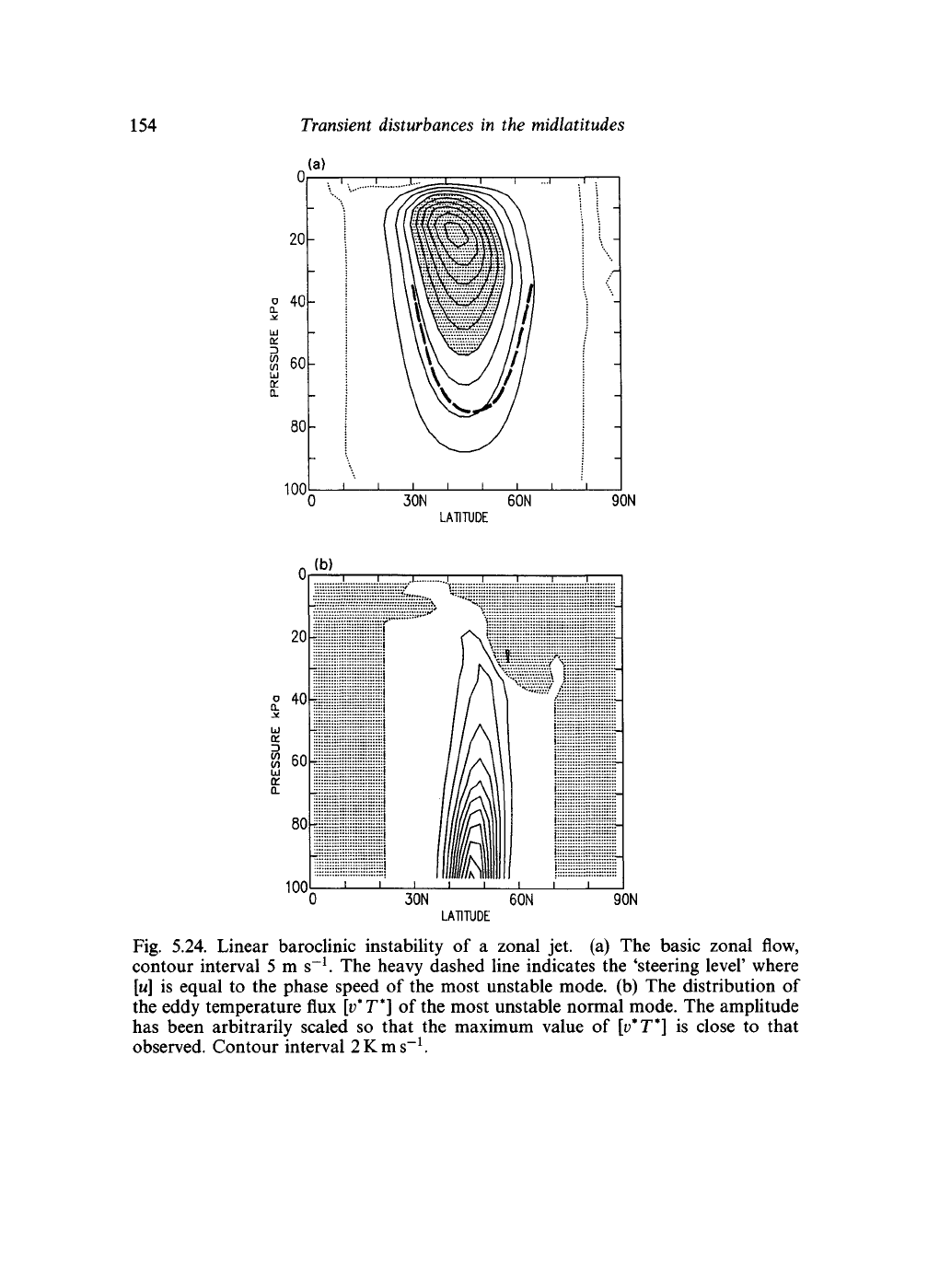
Figure 5.24 shows the results of such a calculation for a realistic jet-like

basic flow. In fact, this calculation was carried out for an atmosphere on a

sphere. The basic wind and temperature fields were discretized on to a grid

(j)

and p, and the rate of change of perturbation velocity, temperature and

surface pressure was calculated using a primitive equation numerical model.

The normal modes of the system, including the unstable normal modes, were

calculated by determining the eigenvalues and eigenvectors for a resulting

595 x 595 matrix with complex coefficients. This is no small computational

problem, and requires a large computer to be practicable. In some respects,

the results do not differ greatly from the most unstable normal mode in

the corresponding Charney mode. The growth rate is 0.706 day"

and the

phase speed is 11.9° of longitude per day. The steering level corresponding

to this phase speed is sketched on the zonal wind cross section; its height

varies with latitude, being nearest to the ground in the centre of the jet. The

temperature fluxes are poleward, confirming that the energy conversions

are those of baroclinic instability. They are large below the steering level

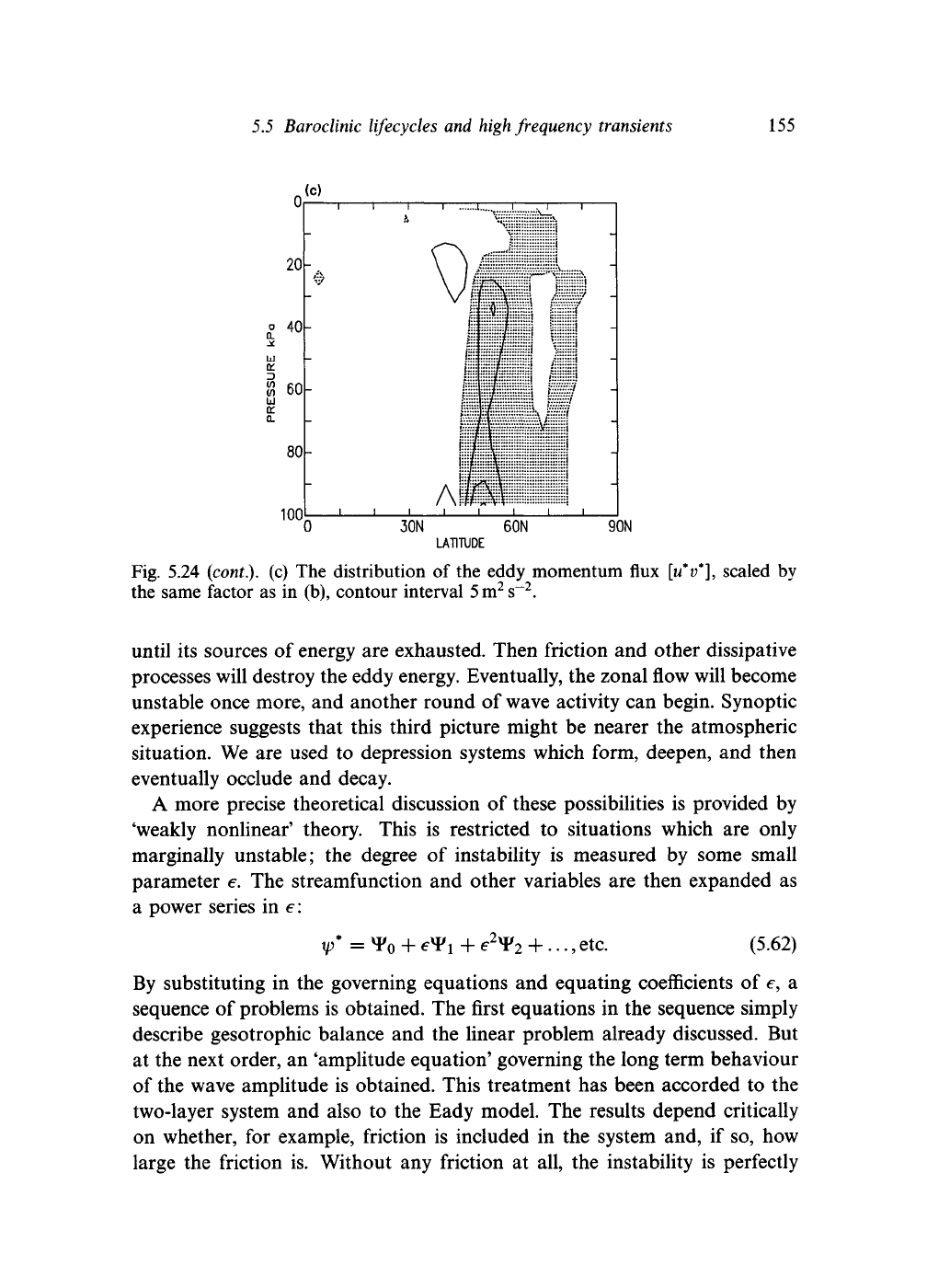
and decrease in the upper troposphere. The new element is the poleward

momentum flux. This tends to be poleward south of the jet (where [u]

positive) and equatorward to the north of the jet (where [u]

is negative);

consequently, the momentum flux represents a conversion of eddy kinetic

energy to zonal kinetic energy, as shown by Fig. 5.14. The effect of the

momentum fluxes is to offset the growth of eddy energy.

5.5 Baroclinic lifecycles and high frequency transients 153

Although the distribution of eddy momentum flux with latitude is similar

to that observed, the maximum is too low in the troposphere and its magni-

tude is much too small relative to the temperature fluxes. We conclude that

the linear theories of this section give a reasonable account of the observed

scale, growth rates and temperature flux distribution of the transient eddies.

But they do not account very well for the observed momentum fluxes, and

they in no way predict the actual levels of eddy activity to be expected.

Linear theory has its limitations!

5.5 Baroclinic lifecycles and high frequency transients

Linear theory of baroclinic instability, such as the Eady model, is based on a

linearization of the equations. The amplitude of disturbances is assumed to

be so small that products of eddy quantities can be neglected. If instability

is present, disturbances of certain wavelengths will amplify exponentially,

and will dominate the flow after a sufficient time. But as the unstable eddies

continue to grow, the assumptions permitting the linearization will eventually

break down. In the language of global circulation studies, the eddy fluxes of

temperature, momentum, and so on, will become so large that they begin to

modify the zonal mean temperature and wind fields. What will happen then?

If baroclinic instability is responsible for generating the transients observed

in the tropospheric midlatitudes, what happens in the atmosphere?

We might imagine a number of possibilities. The simplest is that as the

growing wave modifies the zonal mean field, it should reduce and eventually

remove the available potential energy which provides the source of energy for

the instability. The wave might then equilibrate with some finite amplitude,

with small conversions which enable a balance to be maintained between

the generation of AZ by differential solar heating, and the destruction of

kinetic energy by friction. Something like this can apparently take place in

laboratory systems (see Section 10.5). For a range of parameter settings,

experiments with rotating baroclinic fluids exhibit a regime of 'regular wave'

behaviour, in which a strong wave with constant or, at most, regularly

fluctuating, amplitude propagates around the apparatus. Alternatively, the

growing wave might modify the mean flow in such a way as to make it more

unstable, thereby accelerating the growth of the wave. Eventually, some

catastrophic 'breaking' of the wave field will occur, completely wiping out

the wave and the zonal flow upon which it grew. Some fluid instabilities

(such as Kelvin-Helmholtz billows on a stratified, sheared flow) do appear

to have this character. Synoptic scale disturbances do not. The third poss-

ibility is that the wave growth might be episodic, that is, the wave will grow

154

Transient disturbances in the midlatitudes

(a)

30N

60N

LATITUDE

90N

30N

60N

LATITUDE

90N

Fig. 5.24. Linear baroclinic instability of a zonal jet. (a) The basic zonal flow,

contour interval 5 ms"

. The heavy dashed line indicates the 'steering level' where

[u]

is equal to the phase speed of the most unstable mode, (b) The distribution of

the eddy temperature flux

[v*T*]

of the most unstable normal mode. The amplitude

has been arbitrarily scaled so that the maximum value of

[v*T*]

is close to that

observed. Contour interval 2Kms~

5.5 Baroclinic lifecycles and high frequency transients

155

100

60N

LATITUDE

90N

Fig. 5.24 (cont). (c) The distribution of the eddy momentum flux [wV], scaled by

the same factor as in (b), contour interval 5m

until its sources of energy are exhausted. Then friction and other dissipative

processes will destroy the eddy energy. Eventually, the zonal flow will become

unstable once more, and another round of wave activity can begin. Synoptic

experience suggests that this third picture might be nearer the atmospheric

situation. We are used to depression systems which form, deepen, and then

eventually occlude and decay.

A more precise theoretical discussion of these possibilities is provided by

'weakly nonlinear' theory. This is restricted to situations which are only

marginally unstable; the degree of instability is measured by some small

parameter e. The streamfunction and other variables are then expanded as

a power series in e:

ip*

(5.62)

By substituting in the governing equations and equating coefficients of 6, a

sequence of problems is obtained. The first equations in the sequence simply

describe gesotrophic balance and the linear problem already discussed. But

at the next order, an 'amplitude equation' governing the long term behaviour

of the wave amplitude is obtained. This treatment has been accorded to the

two-layer system and also to the Eady model. The results depend critically

on whether, for example, friction is included in the system and, if so, how

large the friction is. Without any friction at all, the instability is perfectly

156 Transient disturbances in the midlatitudes

reversible. We find that the wave grows to a maximum amplitude, then

begins to decline until it returns to its original amplitude. This cycle repeats

indefinitely, and its character is determined by the initial conditions. Such

a model is not very realistic, since in a real situation, friction will always

be present. If friction is substantial, the wave will simply equilibrate to

some fixed amplitude such that the generation of eddy kinetic energy exactly

balances its dissipation by friction. In the case when the friction is small but

not zero (i.e. proportional to some small power of

e),

more complicated and

more interesting behaviour can be found. The wave can settle into a pattern

of regular oscillations or 'vacillations' which are independent of the initial

conditions. In some cases, these vacillations can be irregular or 'chaotic'.

Such analyses are mathematically rather complex, and since they rest on

very artificial assumptions of marginal instability which are perhaps rarely

realized in practice, they are not necessarily relevant to the actual evolution

of unstable disturbances. Numerical integration provides a more accessible,

and perhaps not much less general, approach to the problem.

A classical numerical experiment is to determine an unstable eigenmode

of a given zonal flow, such as was shown in Fig. 5.24, and to use this as

initial data for a numerical integration of the full nonlinear equations of

motion. In the simplest such experiments, there is no friction or heating, so

that any chosen initial

[u]

and the [6] field in thermal wind balance with

it is an exact solution of the governing equations. The initial jet is chosen

to be representative of the observed midlatitude tropospheric jet. Provided

the eigenmode has sufficiently small amplitude to begin with, the nonlinear

terms are negligible and the wave simply amplifies exponentially. As the

wave amplitude becomes finite, the zonal flow begins to change, and the rate

of increase of amplitude becomes less rapid. Eventually, the wave reaches

a maximum amplitude. Thereafter, for a large number of realistic initial

jets,

the waves collapse, often very rapidly, leaving a final state of zonal

flow, though with the jet profoundly modified by the wave event. Such a

sequence has been called a 'baroclinic wave lifecycle', and it has much in

common with the observed synoptic evolution of midlatitude disturbances

in the atmosphere.

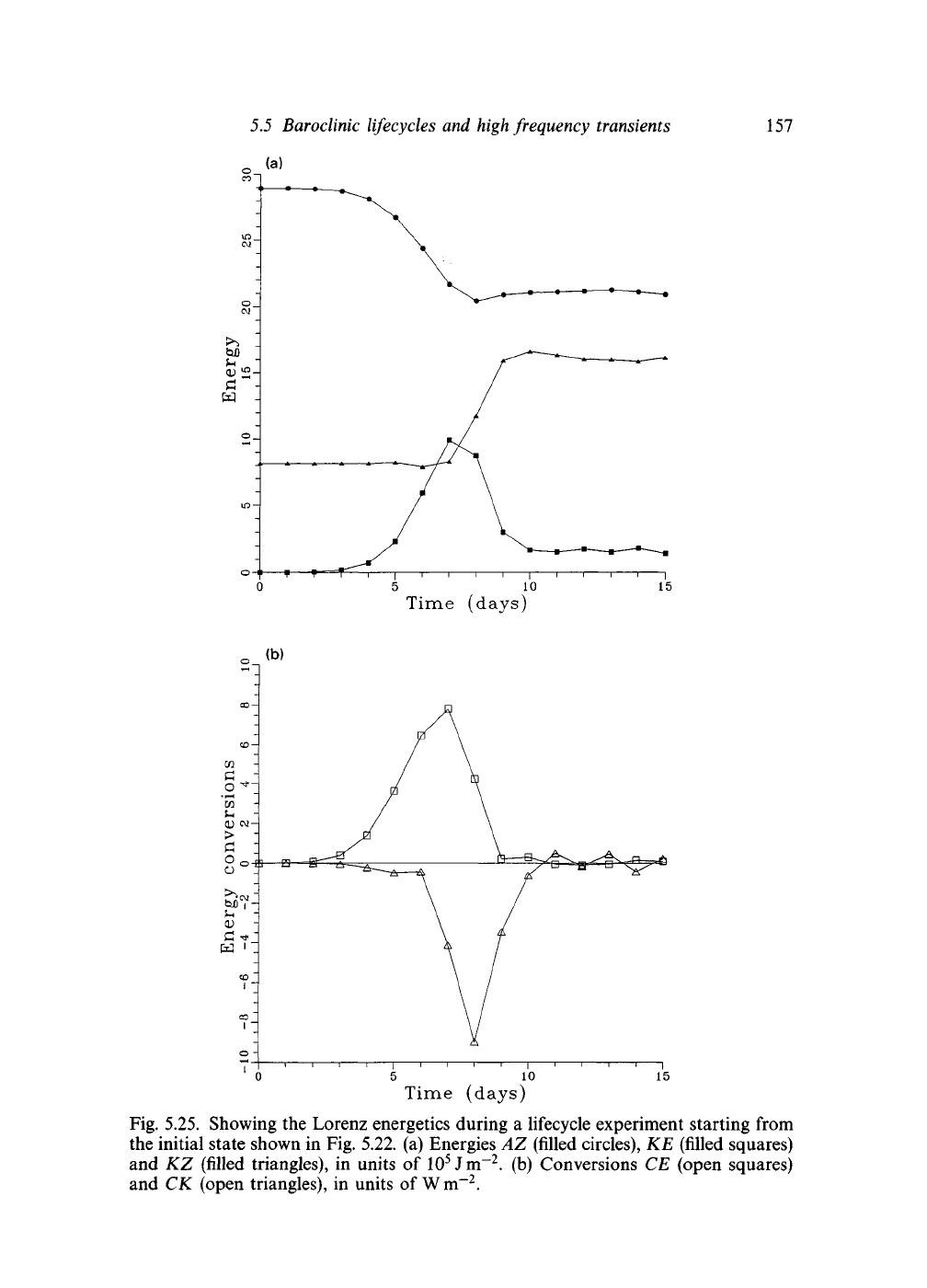
Figure 5.25 shows the energetics of such a lifecycle. In the linear phase,

KE increases exponentially, while AZ and KZ remain more or less steady.

As the growth of KE levels off in the mature stage, a drop in AZ reveals

the modification of the zonal flow. The decay phase is characterized by a

rapid drop of KE and a corresponding increase of KZ. During the growth

stage, the conversions are dominated by CA and C£, indicating that the

temperature fluxes are poleward, upward and large. In the mature stage,

5.5 Baroclinic lifecycles

and

high frequency transients

157

Time (days)

Fig. 5.25. Showing the Lorenz energetics during

lifecycle experiment starting from

the initial state shown in Fig. 5.22. (a) Energies

(filled circles),

(filled squares)

and

(filled triangles),

units

Jm"

(b)

Conversions CE (open squares)

and

(open triangles),

units ofWm"

158 Transient disturbances in the midlatitudes

30N

60N

LATITUDE

30N 60N

LATITUDE

90N

30N

60N

LATITUDE

30N

60N

LATITUDE

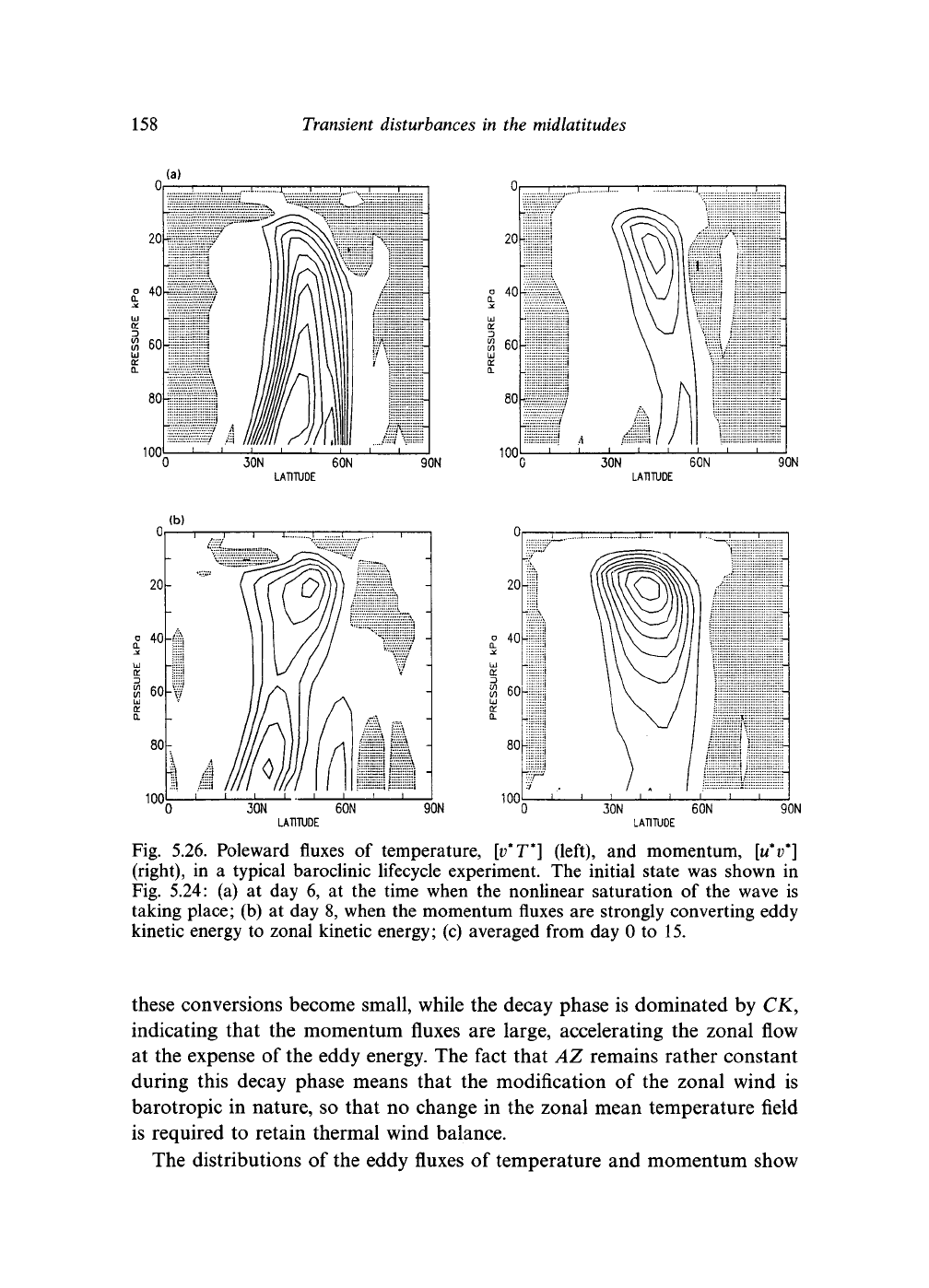
Fig. 5.26. Poleward fluxes of temperature, [v*T*] (left), and momentum, [u*v*]

(right),

in a typical baroclinic lifecycle experiment. The initial state was shown in

Fig. 5.24: (a) at day 6, at the time when the nonlinear saturation of the wave is

taking place; (b) at day 8, when the momentum fluxes are strongly converting eddy

kinetic energy to zonal kinetic energy; (c) averaged from day 0 to 15.

these conversions become small, while the decay phase is dominated by CK,

indicating that the momentum fluxes are large, accelerating the zonal flow

at the expense of the eddy energy. The fact that AZ remains rather constant

during this decay phase means that the modification of the zonal wind is

barotropic in nature, so that no change in the zonal mean temperature field

is required to retain thermal wind balance.

The distributions of the eddy fluxes of temperature and momentum show