Jean-Laurent Mallet. Geomodeling
Подождите немного. Документ загружается.


118
CHAPTERS.
TESSELLATIONS
Figure 3.13
Linking
the
closest
points
p*(fc)
and
q*(/i)
of two
closed
curves
can
lead
to the
construction
of
an
incorrect
skin
between
these
two
curves.
3.3.3
Skin Algorithm
Formulating
the
problem
As
shown
in figure
(3.12),
let us
consider
two
closed
3D
polygonal curves
C(P*)
and
C(Q*}
denned
by two
ordered sets
P*
and
Q*
of
M
and N
vertices
assumed
to be
numbered
4
as
follows:
and
By
definition,
we
call "skin algorithm"
any
method allowing
a
triangulated
surface
T
whose boundary
is
identical
to the
union
of
C(P*)
and
C(Q*)
to be
built:
Solution derived
from
the
strip algorithm
Let
us cut the
curves
C(P*)
and
C(Q*)
at
nodes
p*(fc)
e
P* and
q*(/i)
e
Q*,
and
let P and Q be the new
point
sets
obtained
by
renumbering
P* and Q*
as
follows:
Prom
P and Q so
defined,
two
new, open polygonal curves C(P)
and
C(Q]
whose
geometry
is the
same
as
C(P*}
and
C(Q*)
can be
built
and the
strip
4
The
notation
(a%6)
represents
the
rest
of the
division
of a by b.

3.3.
NON-DELAUNAY TRIANGULATED SURFACES
119
Figure
3.14
Installing
links
between
two
closed
curves
enables
us to
constrain
the
shape
of
the
skin
joining
these
two
curves.
algorithm
thus used
for
building
a
triangulated
surface
between
C(P)
and
C(Q).
The
only
difficulty
arises when choosing
the
points
p*(fe)
6
P*
and
q*(/i)
6
Q*.
A
naive solution consists
in
choosing these
two
points
to
minimize
||p*(&)
—
q*(/i)||
-
this
can
lead
to
surprising results such
as the one
shown
in
figure
(3.13).
In
practice,
a
better choice
of the
pair
of
points
(p*(fc),q*(/i))
can be
obtained
as
follows:
•
Build
the 3D
Delaunay's
tessellation
D(P*
U
Q*)
of the
point
set (P* U
Q*).
•
Extract
the
convex
hull
of (P* U
Q*}
which,
according
to
property
(-D3)
page
101,
is the
boundary
<9£>(P*
U
Q*}
of
V(P*
U
Q*).
•
Look
for the
shortest
edge
(p*(fc),
q*(/i))
belonging
to
dT>(P*
U
Q*)
and
such
that
p*(fc)
€
P* and
q*(/i)
€
Q*.
Taking
links
into
account
The
skin algorithm described above
is
fully
automatic
and may
produce solu-
tions
that
do not
cope
perfectly
with
the
triangulated
surface
shape initially
sought
by the
user.
For
example,
in
figure
(3.13),
it can be
seen
that
this
algorithm
correlates
the
points
of
C(P*)
and
C(Q*)
automatically, without
taking
into account
the
similarities between these
two
curves.
As
shown
in
figure
(3.14)
and to
take these similarities into account, some
links
between pairs
of
points
(p*(fc),q*(/i)},
located
on
C(P*)
and
C(Q*),
respectively, have
to be
installed manually.
These
pairs
of
points
split
the
closed
curves
C(P*)
and
C(Q*)
into
a
series
of
pairs
of
open curves
to
which
the
strip algorithm
can
then
be
applied (see
[70]).
3.3.4 Pants Algorithm
Formulating
the
problem
Let us
consider
two
families
of
closed curves given
in the 3D
space:
• a
family
{C(P«)
: a =
1,..
.,ra}
consisting
of
closed
curves
"more
or
less"
located
in a
plane
A,
and

120
Figure
3.15
An
example
of
pants joining
two
families
of
3D
closed
curves.
• a
family
{C(Q*p)
:
/3
=
l,...,n}
consisting
of
closed
curves
"more
or
less"
located
in a
plane
B.
Moreover,
we
assume
that
A and B are
"more
or
less" parallel
in the
sense
that
these
planes
eventually
intersect,
far
from
the
curves
{C(P*}}
and
{C(Q^}}.
For
example,
as
shown
in figure
(3.15),
if ra
=
1 and n — 2,
then
these
two
families
of
curves
can be
considered
as the
pants'
boundary.
For
this reason,
we
propose calling
"pants
algorithm"
any
method
that
allows
the
construction
of
a
continuous surface whose boundary
is
coincident with
two
given families
of
curves
(C(P*)}
and
{C(Q*
p
)}.
Solution
derived
from
the
skin
and
patch
algorithms
As
you can
see,
the
pants
problem
is a
generalization
of the
skin problem.
A
solution based
on a
four-step algorithm using
the
patch
and
skin algorithms
already
presented
in
sections
(3.3.1),
and
(3.3.3)
is
proposed
below.
For the
sake
of
simplicity,
we
will assume
that
{C(P*}}
and
{C(Q*p)}
are
planar
and
that
planes
A and B do not
intersect:
Step
1 — In the
plane
A,
build
a
closed curve
C(P*)
containing
all the
curves
{C(P*}}.
—
Use the
constrained Delaunay's tessellation algorithm (see
page
105)
for filling the gap
between
C(P*)
and the
family
{C(P*}}
with triangles (see
top figure
(3.16)).
—
Displace
C(P*)
toward
the
plane
B one
third
of the
distance
between
planes
A and B
(see bottom
figure
(3.16))
Step
2 —
Perform
the
same operations
as in
step
1
above
on the
second
family
of
curves
{C(Q*p}}.
CHAPTER 3. TESSELLATIONS
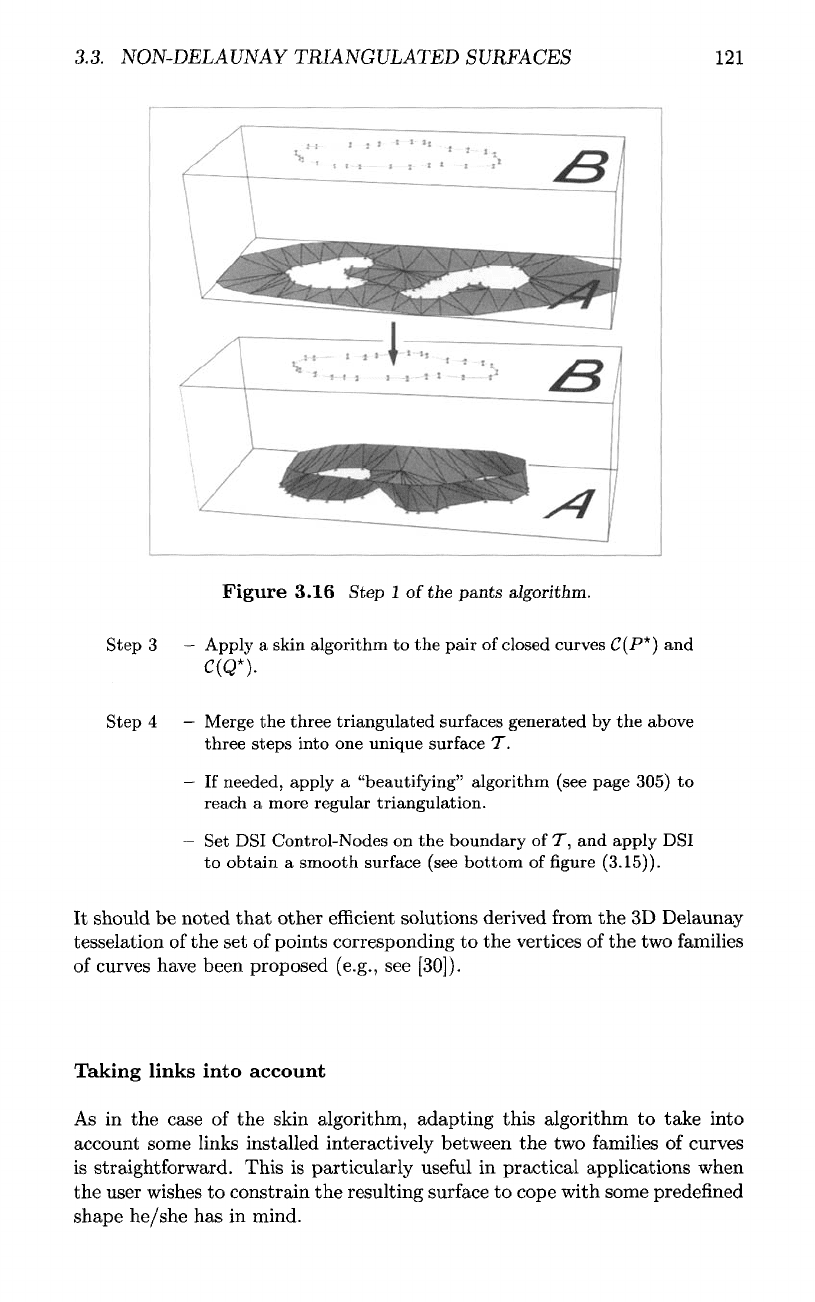
3.3.
Figure
3.16 Step
1
of
the
pants algorithm.
Step
3 —
Apply
a
skin algorithm
to the
pair
of
closed curves
C(P*)
and
C(Q*).
Step
4 —
Merge
the
three triangulated surfaces generated
by the
above
three
steps
into
one
unique
surface
T.
—
If
needed, apply
a
"beautifying" algorithm (see page 305)
to
reach
a
more regular triangulation.
—
Set
DSI
Control-Nodes
on the
boundary
of T, and
apply
DSI
to
obtain
a
smooth
surface
(see bottom
of
figure
(3.15)).
It
should
be
noted
that
other
efficient
solutions
derived
from
the 3D
Delaunay
tesselation
of the set of
points
corresponding
to the
vertices
of the two
families
of
curves
have
been
proposed
(e.g.,
see
[30]).
Taking
links
into
account
As
in the
case
of the
skin
algorithm,
adapting
this
algorithm
to
take
into
account
some
links
installed
interactively
between
the two
families
of
curves
is
straightforward.
This
is
particularly
useful
in
practical
applications
when
the
user
wishes
to
constrain
the
resulting
surface
to
cope
with
some
predefined
shape
he/she
has in
mind.
NON-DELAUNAY TRIANGULATED SURFACES
121

122
Figur e
3.17
An
example
of a
regular
3-grid
embedded
in the
1R
3
space.
As
you can
see,
this
grid
is cut by a set
of
geological
faults
that
generate split nodes.
The
geometry
of the
cubic
3-cells
bordering
the
faults
has
been
adjusted
to fit the
geometry
of
these faults.
3.4
Notion
of a
regular
n-grid
3.4.1
Definition
Let
us first
consider
an
n-dimensional
parametric
space
M
n
associated
with
the
following
entities:
•
{Uk
1
...k
n
}
is the
infinite family
of
n-cells
of
M
n
corresponding
to
generalized
5
unit parametric squares defined
by
where
u
1
is the
ith
coordinate
of u,
while
ki is
assumed
to be a
nonnegative
integer.
RNi...N
n
is a
"rectangular" closed
region
6
of
M
n
defined
7
by
where
{Ni,...,
N
n
}
are
assumed
to be
n
given positive integers.
5
The
cells
{C/fe
1
...fc
n
}
are
actual
squares
only
in the
case
where
n = 2.
6
Such
a
region
is
actually
a
rectangle
only
in the
case
n = 2.
7
Note
that
Uk
l
...k
n
is the
closure
of
Uj
tl
...k
n
(
see
definition
on
page
31).
CHAPTER 3. TESSELLATIONS

3.4.
NOTION
OF A
REGULAR
N-GRID
123
Let
m
>
n be a
given integer,
and let
x(u)
=
X(M
I
,
..
.,w
n
)
be a
mapping
8
from
JR
n
to
JR
771
.
By
definition,
the
image
GNi...N
n
of the
parametric rectangle
RNi...N
n
is
called
a
regular (curvilinear) n-grid
of
JR
m
,
while
the
image
Ck^...k
n
of
any
unit parametric square
Uk
l
...k
n
is
called
an
n-cell
of the
regular n-grid:
One
can
observe
that
the
n-cells
{Ck
1
...k
n
}
so
denned
generate
a
partition
of
the
regular n-grid:
Most
of the
time
in
geological applications,
the
embedding space
has a di-
mension equal
to m = 3. An
example
of a
regular 2-grid
can be
seen
in
figure
(6.22),
and an
example
of a
regular 3-grid embedded
in the
1R
3
space
is in
figure
(3.17).
Practical
convention
From
a
practical
point
of
view,
from
now on, we
will
assume
that
there
is an
implicit
cellular decomposition
of the
boundary
of
each cells
C'fc
1
...fc
n
such
that
the
i-cells
of
dCk-^...k
n
are
the
images
of the
^-cells
of
dU^...^-
In
particular:
• the
vertices
of
dCki...k
n
are
the
images
of the
vertices
of
dUk
l
...k
n
,
• the
edges
of
dCk
l
...k
n
are the
images
of the
edges
of
dUk
l
...k
n
,
• the
faces
of
<9Cfe
1
...fe
n
are the
images
of the
faces
of
5f/fc
1
...fe
rt
,
• and so on.
As
a
consequence,
we can
consider
the
n-cells
{C^...^}
as
generalized "curvi-
linear"
rectangles,
9
and the
associated regular n-grid
as a
curvilinear grid.
Importance
of
regular
3-grids
in
sedimentary
geology
As
shown
in
figure
(3.17), regular curvilinear 3-grids
are
particularly well
adapted
to the
modeling
of
geological stratigraphic layers.
In
this particular
case,
as
suggested
in figure
(10.1),
the
following
notations
for the
components
of
the
parameter
u are
traditionally used
and
these
curvilinear
coordinates
(w,
v
:
w)
are
interpreted
as
follows:
8
Note
that
x(u)
may be
discontinuous:
in
geology,
such discontinuities
occur
in the
case
where
JR
n
is
affected
by
some
faults.
9
The
cells
{Cfc
1
...fc
n
}
are
actual
curvilinear
rectangles
only
in the
case
where
n — 2.

124
Figur e
3.18
An
example
of
a
regular
curvilinear
3-grid
fitting the
geometry
of
a
paleo-channel.
Each
section
is
modeled
as a
Coons
patch
(A*,
B*,
C*,
D*)
deduced
by
curvilinear
transformations
of
the
boundaries
of
a
rectangle
(A,
B,
C, D).
• w
corresponds
to the
"paleo-vertical"
direction orthogonal
to the
layer
that
can be
considered
as the
"geologic-time" axis. Implicitly,
it is
assumed
that
there
is an
unknown monotonic increasing
function
10
t =
t(w)
linking
the
geological time
t to w.
•
(u,
v)
corresponds
to the
"pseudo-horizontal"
surface
parallel
to the
layer
that
can be
interpreted
as the
"paleo-horizon"
at the
time
t =
t(w)
of
deposition.
In a
way,
we can
consider
(w,
v) as
"paleo-geographic
coordinates"
at
geological deposition time
t =
t(w).
In
other words, thanks
to an
adequate parameterization, regular
3-grids
can
capture
not
only
the
geometry x(u)
of the
layers,
but
also
information
related
to the
geological depositional process.
In
practice,
if
needed, such information
can be
used
by
numerical geology algorithms such
as, for
example,
balanced
re-
constructions [160,
95,
236]
and
depositional models (e.g.,
see
section (10.3.5)
page 556).
Other types
of
parameterizations
can be
found
to
cope with
the
geometry
of
complex geological bodies
[200].
For
example,
figure
(3.18) shows
a
3-grid
modeling
the
geometry
and the
internal structures
of a
paleo-channel:
In
this
case,
u
1
corresponds
to the
stream lines while
(u
1
,^
2
)
define
the
sections
of
the
channel.
3.4.2
n-GMap associated with
a
regular
n-grid
As
shown
in
figure
(3.19),
the
abstract
topological space (see page
44) as-
sociated with
a
regular n-grid
is
generally
identified
with
its
n-dimensional
parametric
space.
In
this
parametric
space,
it is
easy
to
build
the
n-GMap
Q(D,
ao,...,
a
n
]
associated with
the
partitioning
of the
regular n-grid
GjVi...JV
n
induced
by the
unit parametric squares:
10
Note
that
pinchouts
and
unconformities
may
generate
discontinuities
for the
"geological
time"
function
t =
t(w).
CHAPTER 3. TESSELLATIONS

3.4.
NOTION
OF A
REGULAR
N-GRID
125
Figure
3.19
The
parametric space
of a
regular n-grid plays
the
role
of ab-
stract topological space where darts
are
represented
by
small, white, bullet-headed
segments.
In
this space, cracks
are
installed
in
order
to
introduce geometric discon-
tinuities
in the
regular grid.
The
vertices
of
the
n-cells
incident
to
cracks
are
called
"Split
Nodes."
• For
each unit parametric square
Uki...k
n
,
there
are
exactly
n-darts
associated
with each
of its
2
n
vertices.
As a
consequence,
the
total
number
\D\ of
darts
contained
in D is
such
that
• For
each positive integer
i < n, an on
link
is
installed between each pair
of
darts
(d,
d'}
associated
with
a
common vertex
of two
adjacent
^-cells
of the
same unit parametric square
Uk
1
...k
n
-
• An
Oi
n
link
is
installed
between each pair
of
darts
(d,
d')
incident
to the
same
vertex
and
belonging
to two
"topologically"
adjacent unit parametric squares
U
kl
...k
n
and
C/fc/...^.
It
should
be
noted
that
two
"geometrically"
adjacent
unit
parametric
squares
Uki...k
n
an
d
Uk
1
...k
1
mav
n
°t
be
"topologically"
adjacent
(see figure
(3.19)).
If
the aim is to
introduce
a
discontinuity
along
an (n
—
l)-cell
called
"crack"
shared
by
U^
...k
n
and
U#
.../^,
then
the
a
n
links
between
pairs
of
darts
(d,
d'}
incident
to
such
a
crack
have
to be
changed
as
follows
to
introduce
a new
boundary
along
the
common
(n
—
l)-cell
corresponding
to the
crack:
3.4.3
Discrete model
As
discussed
on
page
65, for
each
positive
integer
i
e
[0, n], it is
possible
to
associate
a
discrete
model
A'f
p
(0j,
A^,
(^C^J
with
any
n-Gmap.
In the
specific
case
where
a
n-GMap
is
associated
with
a
regular
n-grid,
particular
attention
is
usually
paid
to the
cases
i = 0 and i = n:
•
M.
p
(£lo,
TVio,
tpo,C<p
0
)
is
called
a
"corner
point"
model
and
corresponds
to
the
modeling
of p
parameters (discrete embedding) attached
to the
vertices
of
the
regular n-grid.
In
practice, such
a
model
is
often
used
for
modeling
the
geometry x(u)
of the
grid and,
in
this case,
p =
m
and
</?o
=
x.

126
Figur e
3.20
Parametric
representation
of a
2-cell
C
belonging
to a
regular
2-grid:
the
parametric
domain
consists
of
a
unit
square
[0,1]
2
.
•
M.
p
(£l
n
,
N
n
,
VmCpn)
is
called
a
"cell
centered"
model
and
corresponds
to
the
modeling
of p
parameters
(discrete
embedding)
attached
to the
n-cells
of
the
regular
n-grid.
In
practice,
such
a
model
is
often
used
for
modeling
the
physical
properties
of the
grid
cells.
In
geological
applications,
for n
<
3,
most
of the
time regular
n-grids
are
embedded
in the (x,
y,
z)
space
in a
curvilinear
way to fit
with
the
geometry
of
geological objects.
For
example,
figure
(3.18) shows
a
regular 3-grid
fitting
the
geometry
of a
paleo-channel.
Barycentric
parameterization
of the
cells
First,
consider
a
regular
1-grid.
Each cell
C is a
segment
{x(ao),x(o;i)}
and
there
is a
one-to-one parametric representation
x(w)
that
transforms
the
unit
segment
[0,1]
into
C:
In
this parametric representation
of (7, the
weighting
functions
bi(u)
are as-
sumed
to be
defined
as
follows
while
nodes
{QO,
cti}
correspond
to the
vertices
of
C.
By
definition,
the
coeffi-
cients
bi(u)
and
62(u)
are
called
the
"barycentric
coordinates"
of
x(u) relative
to the
vertices
x(cno)
and
X(Q;I),
respectively, while
u is
called
its
"local nor-
malized
coordinate" relative
to
C.
More
generally,
any
cell
C of a
regular n-grid
can be
parameterized
as
CHAPTER 3. TESSELLATIONS

3.4.
NOTION
OF A
REGULAR
N-GRID
127
follows
on the
unit
hypercube
[0,
l]
n
:
In
this definition
of
x(u),
the set of
nodes
{o^...^}
consists
of the
2
n
vertices
of
C
assumed
to be
numbered
as
suggested
in
figure
(3.20)
in
such
a way
that
By
definition,
the
coefficients
{bi
1
(w
1
),...,
bi
n
(u
n
}}
are
called
the
"barycentric
coordinates"
of
x(u)
relative
to the
vertices
of
C,
while
{w
1
,...,
u
n
}
are
called
its
"local normalized coordinates" relative
to C.
Let
us now
address
the
problem
of finding the
parameter
u
=
[u
1
,...,
u
n
]
that
corresponds
to the
location
of a
given point
p =
x(u)
inside
the
cell
C.
According
to
equation (3.14), this parameter
is the
solution
of the
following
system
of
m
nonlinear equations where
{p
j
}
and
(x^a^...^)}
represent
the
coordinates
of the
points
{p}
and
(x(o;j
1
...i
n
)}
in the
M
m
embedding
space,
respectively:
If
U[j]
is a
given initial estimation
of the
solution, then
the
problem reduces
to the
determination
of an
increment
Au
such
that
/
J
(u^]
+ Au) is
equal
to
zero
for all
j.
According
to the
Taylor series expansion
formula
(4.27),
this
is
equivalent
to
saying
that
Au
should
be
such
that
By
introducing
the n x n
square matrix
D as
defined
by
the
solution
of the
system
of
equations (3.15)
can be
written
as
follows:
It can be
observed
that
the
dimension
m of the
embedding space
is
greatei
or
equal
to the
topological dimension
n of the
grid. This system
of
equations
can
be
solved
in a
least
square
sense
as
follows:
