Кармелюк Г.І. Теорія ймовірностей та математична статистика

Подождите немного. Документ загружается.

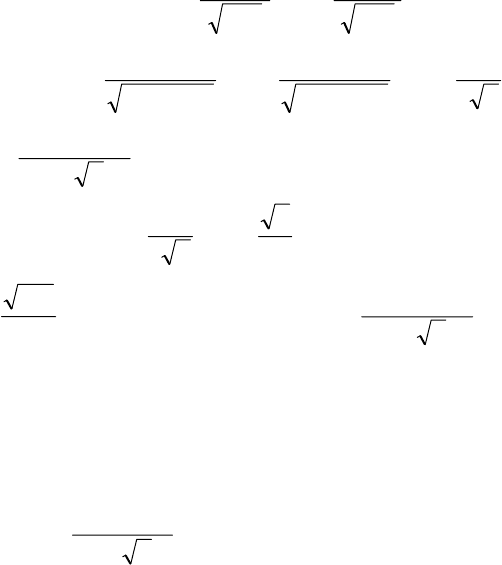
241

Розв’язок.

Імовірність настання події в кожному з випробувань

(дослідів) рівна р = 0,9, q = 1 – р = 0,1. Число випробувань

(дослідів) n > 150, тобто велике, так що

⋅

1,09,0150npq

95,13 >= . Оскільки в задачі задана 98,0)150( ≥

≤

nkP

то для знаходження числа випробувань n використаємо

інтегральну формулу Лапласа:

;)(

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=≤≤

npq

npk

npq

npk

ФkkkP

−

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

≤

39,01,0

9,0150

9,01,0

9,0

98,0

3,0

9,0150

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

−

Оскільки

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

при n > 150 рівна

5,0499972,0

150

≈=

⎟

⎠

⎞

⎜

⎝

⎛

, то

−≤

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

Φ 5,0

3,0

9,0150

.48,098,0 −≤− Користуючись таблицями інтегральної функ-

ції і враховуючи те, що інтегральна функція непарна і зрос-

таюча, знаходимо значення параметра

054,2

−

≤

t при якому

48,0)( −

≤

tФ . При цьому застосовувалась лінійна інтерпо-

ляція.

Отже,

054,2

3,0

9,0150

−≤

−

Після спрощень отримуємо квадратне рівняння відносно

невідомої n:

242

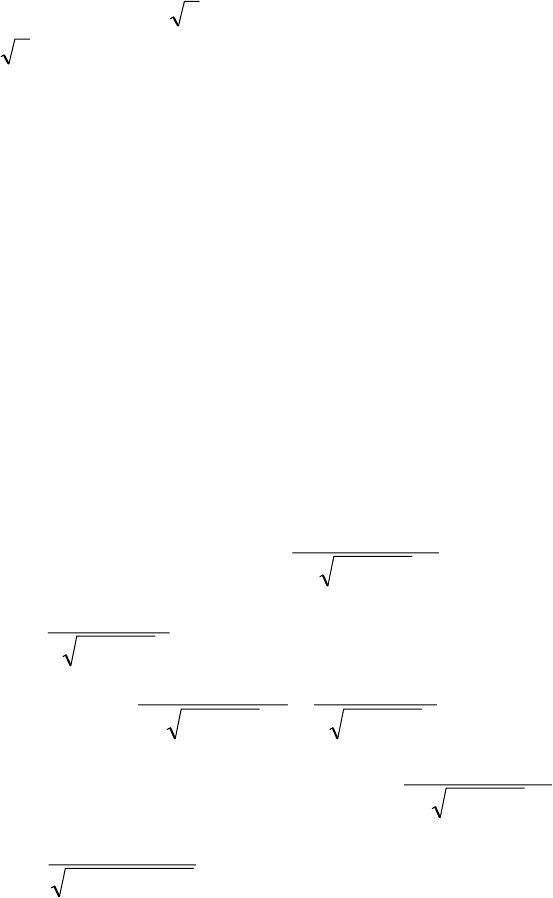
01506162,09,0 =−− nn , розв’язавши яке, отримуємо

2568,13=n (від’ємне значення кореня відкидаємо, як не-

можливе). Остаточно n = (13,2568)

= 175,74.

Оскільки n – ціле число, то n ≥ 176.

3.4.11. Проектується система з n = 6000 вузлів зв'язку, що

може бездоганно працювати при відмові будь-яких k = 150 з

них. Допустима ймовірність відмови системи 0,0015.

Чому дорівнює максимально допустима ймовірність р

відмови окремого вузла? (відмови вузлів незалежні).

Розв’язок.

Випробовується n = 6000 вузлів зв’язку (

n = 6000 повтор-

них незалежних випробувань), імовірність відмови кожного з

яких рівна p (імовірність настання події в кожному випробу-

ванні рівна p). Якщо відмовить k < 150 вузлів, то система буде

бездоганно працювати. Якщо k ≥ 150, то система відмовить.

Імовірність відмови, тобто імовірність настання події

.0015,0)6000150(

6000

≤≤ kP Запишемо дану рівність згід-

но інтегральної теореми Муавра-Лапласа:

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

=≤≤

ФkP

6000

60006000

)6000151(

6000

.0015,0

6000

6000150

⎟

⎠

⎞

⎜

⎝

⎛

−

Оскільки

6000

6000150

6000

60006000

−

⋅

−

то при ймо-

вірності відмови Р < 0,99 значення

⎟

⎠

⎞

⎜

⎝

⎛

⋅−

6000

60006000

.5,0)5(

1,09,06000

9,06000150

=Φ≥

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

= Ф

243

Отже, 0015,0

)1(6000

6000150

5,0 =

⎟

⎠

⎞

⎜

⎝

⎛

−⋅

−

, ;1=

−

=1 .

Тому

9985,00015,05,0

)1(6000

6000150

=−=

⎟

⎠

⎞

⎜

⎝

⎛

−⋅

−

або

9985,0)(

tФ . З таблиць інтегральної функції знаходимо t =

= 2,96.

Отже,

96,2

)1(6000

6000150

−⋅

−

Після спрощень отримуємо квадратне рівняння;

0225007,18525696,36052569

=+− pp , розв’язавши яке

отримуємо р = 0,03169. Від’ємний корінь відкидаємо, як та-

кий, що не задовільняє умову

.0≥p

3.4.12. У великому місті за рік народжується 20000 дітей.

Приймаючи за ймовірність народження хлопчика р = 0,51,

знайти таке число t, щоб з ймовірністю 0,99 можна було б

стверджувати, що серед народжених протягом року в цьому

місті дітей число хлопчиків перевищує число дівчаток не

менше, ніж на t.

Розв’язок.

Позначимо через n

– кількість хлопчиків і n

– кількість

дівчаток серед 20000. Отже n

+ n

= 20000, звідси n

20000 – n

; але tnn

дx

≥− – за умовою, або ≥

−

дд

nn20000

tnt

≥−→≥ 220000 , звідси ;

20000 t

−

≤ −

≤

10000

−

і 0≥

n .

244

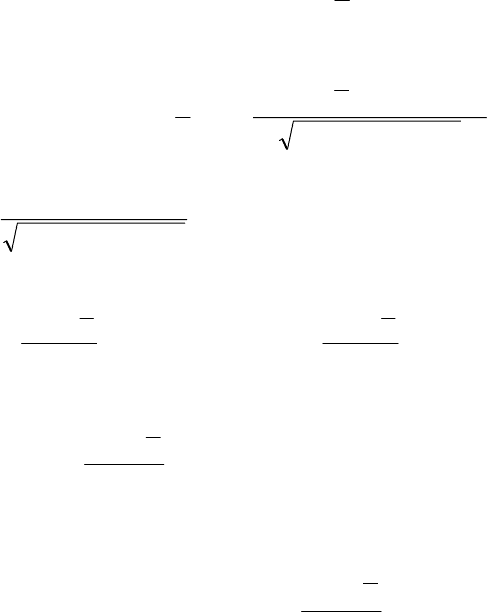
Параметр t знаходимо з умови заданої імовірності 0,99

виконання нерівності

)

100000(

−≤≤ , використавши ін-

тегральну функцію Лапласа:

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−−

=−≤≤

51,049,020000

49,020000

10000

)

100000(

,99,0

51,049,020000

49,0200000

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

−Ф

або

()

.99,05,0

6965,70

200

62065,138

6965,70

200

⎟

⎠

⎞

⎜

⎝

⎛

−

=−−

⎟

⎠

⎞

⎜

⎝

⎛

−

ФФ

Отже,

99,0

6965,70

200

⎟

⎠

⎞

⎜

⎝

⎛

−

З таблиць інтегральної функції знаходимо значення х =

= 2,327 при якому Ф(х) = 0,49; або

327,2

6965,70

200

−

. Звідси

7197,70 ≈=t .

3.4.13. Керуюча ЕОМ обслуговує 1000 виробничих уста-

новок. Ймовірність того, що дана установка в даний момент

часу потребує обслуговування дорівнює а) 0,1; б) 0,01.

Скільки каналів обслуговування r необхідно мати, щоб

ймовірність наявності каналу для кожної установки, що по-

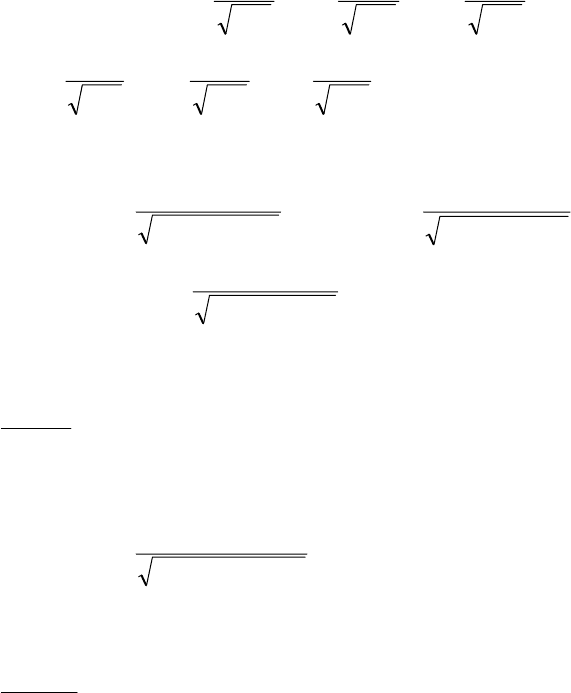
245

требує обслуговування в даний момент часу, була не меншою

0,9?

Розв’язок.

Каналів обслуговування може бути від 0 до r. Імовірність

такої події за умовою задачі не менша 0,9:

≥

≤

)0(

1000

rkP

9,0≥ . Згідно інтегральної теореми Лапласа

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=≤≤

npq

npr

npq

npr

ФrkP

)0(

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−−

npq

npr

npq

Підставимо у дану формулу значення а) n = 1000, р = 0,1,

q = 1 – р = 0,9, отримуємо:

9,0

9,01,01000

1,01000

)( ≥

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅

+ФtФ

, де

9,01,01000

1,01000

⋅⋅

⋅

−

Оскільки

5,0)541,10(

9,01,01000

1,01000

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅

ФФ

, то

4,0)( ≥tФ . За таблицями інтегральної функції Лапласа врахо-

вуючи те, що вона є зростаючою, знаходимо

28,1≥t , тому

28,1

4868,9

100

≥

−r

, звідки 14,112≥r . Отже, умова задачі задово-

льняється при

112≥

б) n = 1000, р = 0,01, q = 1 – р = 0,99, отримуємо:

9,0

99,001,01000

01,01000

)( ≥

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅

+ФtФ

, або +)(tФ

()

9,01782,3 ≥+ Ф . Оскільки 49931,0)1782,3(

≈

Ф , то ≥)(tФ

40069,0≥ . За таблицями знаходимо 28,1≥t , тому

28,1

14643,3

≥

−r

, звідки 027,1428,114643,310

⋅

≥r . Отже,

246

умова задачі задовольняється при

14≥

. Оскільки імовір-

ність

1,001,0 <=p і 1001,01000

⋅

, то для знаходжен-

ня r можна скористуватись формулою Пуассона за методикою

наведеною в задачі 3.2.16. Умова задачі

−

∑

9,09349,0 ≥= задовольняється при k = r = 13; при k = r = 15

99,0

−

∑

3.4.14. В селищі А 2500 жителів. Кожний з них приблизно

6 разів на місяць їде у поїзді в місто В, вибираючи дні поїздок

за випадковими мотивами незалежно від решти жителів.

Яку найменшу місткість повинен мати поїзд, щоб він

переповнювався в середньому не частіше одного разу на 100

днів? (Поїзд йде один раз

на добу).

Розв’язок.

Імовірність того, що будь-який з 2500 жителів їздить у

поїзді в місто В рівна

2,0

==p (кількість днів у місяці

прийнята за 30) і q = 1 – p = 0,8. Ймовірність того, що поїзд

буде переповнюватись не частіше одного разу на 100 днів рів-

на

01,0≤P

. Найбільша гранична місткість поїзда може бути

рівна кількості жителів у селищі, тобто 2500 (k

= n). Най-

менша кількість місць у поїзді k

може бути знайдена з

інтегральної формули Лапласа:

.01,0)(

≤

⎟

⎠

⎞

⎜

⎝

⎛

−

⎟

⎠

⎞

⎜

⎝

⎛

−

=≤≤

npq

npk

npq

npk

ФkkkP

Отже,

−

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

=≤≤

8,02,02500

2,025002500

)2500(

ФkkP

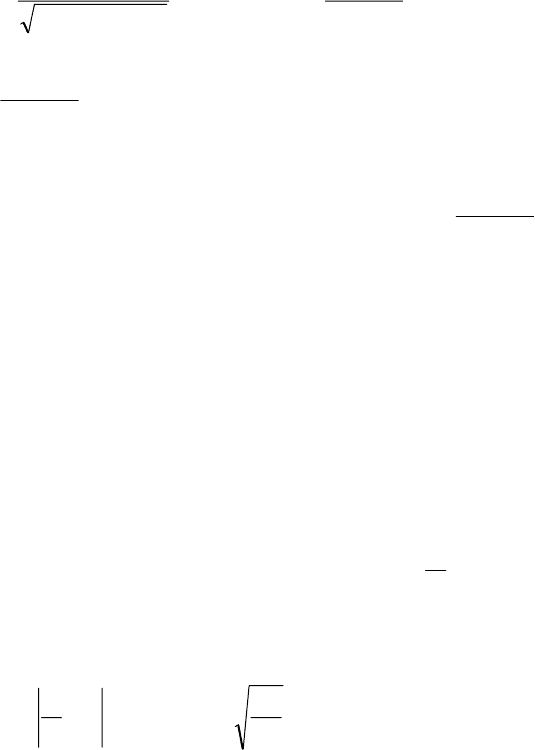
247

.01,0

500

)100(

8,02,02500

2,02500

≤

⎟

⎠

⎞

⎜

⎝

⎛

−

−=

⎟

⎠

⎞

⎜

⎝

⎛

⋅⋅

⋅−

−

ФФ

Оскільки інтегральна функція Ф(100) = 0,5, то

.49,0

500

≥

⎟

⎠

⎞

⎜

⎝

⎛

−

З таблиць інтегральної функції знаходимо значення t, при

якому здійснюється Ф(t) = 0,49. Це значення, t = 2,327. Оскі-

льки інтегральна функція Ф(t)= зростаюча, то

≥

−

500

327,2≥ . Звідки 54750020327,2

⋅

≥k .

Отже, найменша місткість поїзда повинна становити 547

місць.

3.5. Імовірність відхилення відносної частоти події

від її постійної імовірності

Теорема. Якщо імовірність p появи події А в кожному з n

повторних незалежних випробувань постійна і відмінна від 0 і

1 (0 < p < 1), і число випробувань досить велике, то імо-

вірність того, що відхилення відносної частини

події від її

імовірності p за абсолютною величиною не перевищить якого

завгодно малого додатного числа

знаходиться за форму-

лою:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

≤−

Фp

εε

2 (3.5.1).

Задачі

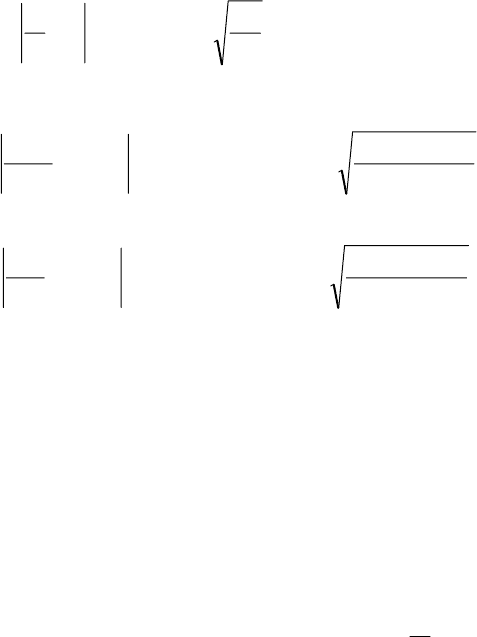
3.5.1. При встановленому технологічному процесі ймовір-

ність бракованих виробів дорівнює 0,015.

248

Визначити ймовірність того, що частота бракованих виро-

бів серед 1000 виготовлених штук буде відрізнятися від ймо-

вірності виготовлення бракованого виробу не більше, ніж на

0,005 в ту чи іншу сторону.

Як зміниться результат, якщо замість 1000 шт. взяти 625?

Розв’язок.

Згідно формули Лапласа дана імовірність рівна:

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

≤−=

Фp

εε

Підставивши числові дані: ε = 0,005; р = 0,015; q = 0,985;

= 1000; n

= 625, отримаємо:

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

≤−

985,0015,0

1000

005,02005,0015,0

1000

()

;807,04033,0230079,12

⋅

== Ф

⎟

⎠

⎞

⎜

⎝

⎛

⋅

⎟

⎠

⎞

⎜

⎝

⎛

≤−

985,0015,0

625

005,02005,0015,0

625

()

6962,03481,020284,12

⋅== Ф .

3.5.2. Французький вчений Бюффон (XVІІ ст.) кинув мо-

нету 4040 разів, причому “герб” з'явився 2048 разів.

Знайти ймовірність того, що при повторенні досліду

Бюффона відносна частота появи “герба” відхилиться від

ймовірності появи “герба” за абсолютною величиною не біль-

шою, ніж в досліді Бюффона.

Розв’язок.

Згідно умови задачі n = 4040; m = 2048, р

= 1/2 –

імовірність випадань “герба”, q = 1/2 – імовірність невипадань

“герба”. Величина відхилення ε відносно частоти

від імо-

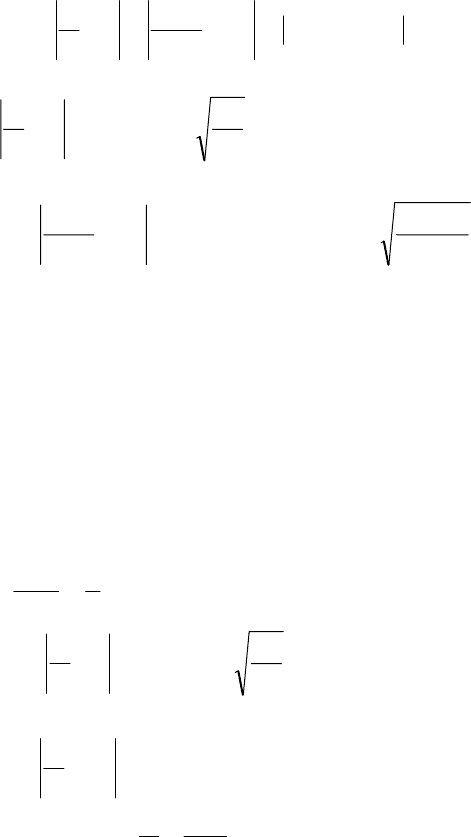
вірності р в досліді Бюффона рівна

249

.0069,05,05069,05,0

4040

2048

=−=−=−= p

Тоді шукану імовірність обчислимо згідно формули

⎟

⎠

⎞

⎜

⎝

⎛

Φ=

⎟

⎠

⎞

⎜

⎝

⎛

≤−

εε

Підставивши необхідні дані,

отримаємо:

⎟

⎠

⎞

⎜

⎝

⎛

⋅

Φ=

⎟

⎠

⎞

⎜

⎝

⎛

≤−

5,05,0

2048

0069,020069,05,0

2048

.6195,030976,02)8771,0(2

⋅=Φ=

3.5.3. В ящику містяться білі і чорні кульки у співвідно-

шенні 4:1. Після вилучення кульки реєструється її колір і

кулька повертається в ящик.

Чому дорівнює найменше число вилучень n, при якому з

ймовірністю 0,95 можна сподіватися, що абсолютна величина

відхилення відносної частоти появи білої кульки від її

ймовірності буде не більшою, ніж

0,01.

Розв’язок.

Імовірність появи білої кульки в кожному вилученні рівна

8,0

. Використаємо формулу:

)

βεε

⎪

⎩

⎪

⎨

⎧

⎟

⎠

⎞

⎜

⎝

⎛

=≤−

Фp

2 .

У задачі р = 0,8, q = 0,2;

= 0,01. Отже,

95,001,08,0 ==

⎟

⎠

⎞

⎜

⎝

⎛

≤−

Тоді,

475,0

95,0

)( ===

tФ . З таблиць інтегральної

функції знаходимо t = 1,96.

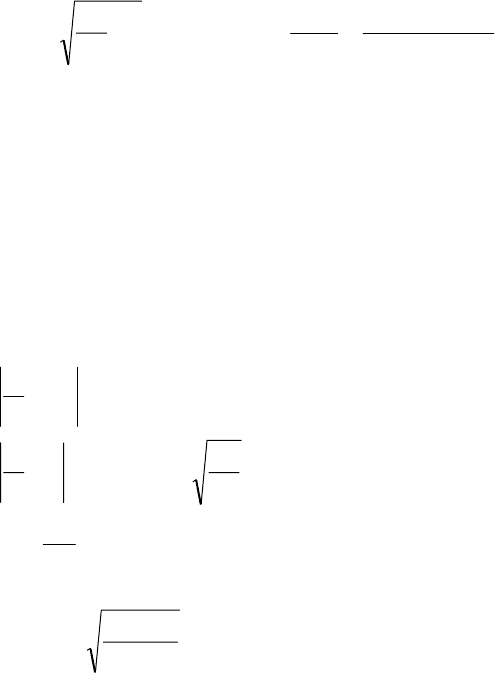
250

Отже, t

, звідки =

⋅⋅

012,0

2,08,096,1

pqt

.614756,6146 ≈=

3.5.4. При штампуванні отримуємо 60% деталей першого

гатунку, 30% – другого і 10% – третього.

Визначити, скільки потрібно взяти відштампованих дета-

лей, щоб з ймовірністю – 0,8, можна було б стверджувати, що

частка деталей першого сорту буде відрізнятись від

ймовірності виготовлення деталей першого гатунку за

абсолютною величиною не більше, ніж на 0,005.

Розв’язок.

Вказівка:

;6,0=p ;4,0

q ;005,0

8,0005,06,0 =

⎟

⎠

⎞

⎜

⎝

⎛

≤−

8,02 =

⎟

⎠

⎞

⎜

⎝

⎛

⎟

⎠

⎞

⎜

⎝

⎛

≤−

Фp

εε

4,0)(4,0

2,0

8,0

)( =→== xФxФ . З таблиці інтегральної

функції знаходимо х = 1,281.

Отже,

281,1

4,06,0

005,0 =

⋅

, звідки 15766

n .

3.5.5. Для космічного корабля імовірність зіткнення про-

тягом однієї години з метеоритом, маса якого не менше від

, дорівнює 0,001. Знайти практично вірогідні межі числа

зіткнень з такими метеоритами протягом трьох місяців польо-

ту з 1 червня по 31 серпня, якщо імовірність практичної віро-

гідності приймається в цьому випадку рівною 0,9995.