Казанцев Э.Ф. Математика. Раздел 4. Теория вероятностей и математическая статистика. Тетрадь 4

Подождите немного. Документ загружается.

д) дис пер сия раз но сти слу чай ных ве ли чин рав на сум ме их дис -

пер сий:

(x – y) = s

(x) + s

(y).

Дей ст ви тель но: x – y = x + (–1) y, то гда

(x – y) = s

(x) + s

[(–1)y] = s

(x) + (–1)

(y) = s

(x) + s

(y).

е) Ес ли есть не сколь ко не за ви си мых слу чай ных ве ли чин x

, x

, …

, то мож но вы чис лить дис пер сию каждой из них:

= E[x

– E(x

)]

; s

= E[x

– E(x

)]

… .

В об щем слу чае: s

= E[x

– E(x

)]

;

ж) мож но вы чис лить дис пер сию сред ней ве ли чи ны:

n n

E x E x E

x x x

E x E x E x

2 2

= - =

+ + +

[ ( )]

( ) ( ) ( )K K

= 1/n

× E{[x

– E(x

)] + [x

– E(x

)] + … + [x

– E(x

)]}

= 1/n ×

s s s

2 2

+ + +K

Ес ли все дис пер сии рав ны ме ж ду со бой, то

s s

2 2

, то есть дис -

пер сия сред ней в n раз мень ше дис пер сии ка ж дой слу чай ной величины.

Тео ре ма 6. Ма те ма ти че ское ожи да ние чис ла на сту п ле ний со бы тия

A в n не за ви си мых ис пы та ний, в ка ж дом из ко то рых оно мо жет на сту -

пить с по сто ян ной ве ро ят но стью p, рав но np, а дис пер сия рав на npq, где

q — ве ро ят ность не на сту п ле ния со бы тия A.

До ка за тель ст во. n — не за ви си мых ис пы та ний — это рас пре де ле -

ние слу чай ных ве ли чин x

, x

, …, x

, вы ра жаю щих чис ло на сту п ле ний со -

бы тия A со от вет ст вен но в 1, 2, …, n-ом ис пы та ни ях — все го n.

Рас смот рим од но из них — 1-е. У не го есть два зна че ния: 0 или 1;

p = 1; q = 0.

Ма те ма ти че ское ожи да ние: E(x

) = x

+ x

= 0 × q + 1 × p = p.

Дис пер сия: s

(x)= E[x – E(x)]

= [x

– E(x)]

+ [x

– E(x)]

= (0 – p)

× q + (1 – p)

p = p

q – q

p = pq(1/(p + q)) = pq.

A все го n — ис пы та ний, сле до ва тель но: E(x) = np; s

(x) = npq.

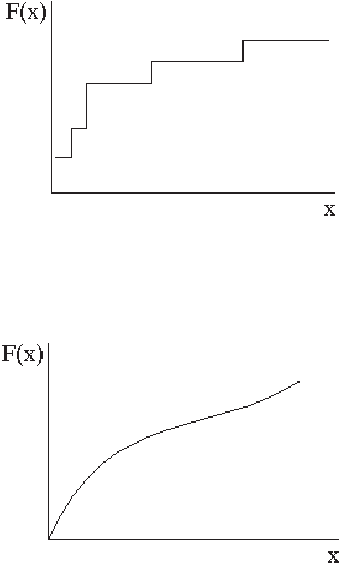
2) Не пре рыв ные ве ли чи ны

Вве дем по ня тие функ ции рас пре де ле ния.

За кон рас пре де ле ния слу чай ной ве ли чи ны кро ме таб лич ной фор -

мы мож но за дать ана ли ти че ски в ви де фор му лы или изо бра зить

графически.

Оп ре де ле ние 4. За ви си мость ве ро ят но сти от те ку щей пе ре мен ной

на зы ва ет ся функ ци ей рас пре де ле ния F(x) или ин те граль ной функ ци ей рас -

пре де ле ния.

Эта функ ция все гда не от ри ца тель на F(x) ³ 0 и она не мо жет быть

боль ше 1: 0 £ F(x) £ 1.

В слу чае дис крет ной слу чай ной пе ре мен ной ве ли чи ны функ ция

F(x) уве ли чи ва ет ся скач ка ми (рисунок 4.3).

В слу чае не пре рыв ной слу чай ной пе ре мен ной ве ли чи на функ ции

F(x) изо бра жа ет ся плав ной, мо но тон но воз рас таю щей кри вой. Эта

функ ция всю ду диф фе рен ци руе ма (рисунок 4.4).

Рис. 4.3

Рис. 4.4

От но ше ние

F x x F x

( ) ( )+ -D

ха рак те ри зу ет плот ность, с ко то рой

рас пре де ля ют ся слу чай ные зна че ния в дан ной точ ке.

В пре де ле при Dx ® 0

lim

( ) ( )

F x x F x

F x f x

+ -

на зы ва ет -

ся плот но стью рас пре де ле ния или плот но стью ве ро ят но сти или диф фе -

рен ци аль ной функ ци ей рас пре де ле ния.

Кри вая, изо бра жаю щая плот ность рас пре де ле ния слу чай ной пе -

ре мен ной на зы ва ет ся кри вой рас пре де ле ния (ри су нок 4.5). Дру ги ми

сло ва ми, кри вой рас пре де ле ния не пре рыв ной слу чай ной ве ли чи ны на -

зы ва ют график ее плотности вероятности.

Тео ре ма 7. Ве ро ят ность то го, что не пре рыв ная слу чай ная ве ли чи -

на x при мет ка кое-ни будь зна че ние в ин тер ва ле (a, b), рав на оп ре де лен -

но му ин те гра лу от ее плот но сти ве ро ят но сти в пре де лах от a до b (ри су -

нок 4.5):

P a x b f x dx F x

( ) ( ) ( )< < = =

Оче вид но, что

f x dx( ) =

-¥

— это пол ная ве ро ят ность.

Оп ре де лим ма те ма ти че ское ожи да ние и дис пер сию не пре рыв ной

слу чай ной величины.

Оп ре де ле ние 5. Ма те ма ти че ским ожи да ни ем E(x) не пре рыв ной

слу чай ной ве ли чи ны x, плот но стью ве ро ят но сти ко то рой яв ля ет ся

функ ция f(x), на зы ва ет ся ве ли чи на ин те гра ла

E x x f x dx( ) ( )= ×

-¥

, ес ли он

схо дит ся аб со лют но.

Рис. 4.5. Кри вая рас пре де ле ния не пре рыв ной слу чай ной величины

Оп ре де ле ние 6. Дис пер си ей не пре рыв ной слу чай ной ве ли чи ны

на зы ва ет ся ве ли чи на ин те гра ла

2 2

( ) ( ) ( )x x a f x dx= - ×

-¥

, ес ли он так же

схо дит ся (a = E(x)).

Свой ст ва ма те ма ти че ских ожи да ний и дис пер сий для не пре рыв -

ных слу чай ных ве ли чин ос та ют ся те же, что и для дискретных.

3)Рас смот рим не ко то рые ти пы рас пре де ле ний.

а) Рав но мер ное (пря мо уголь ное) рас пре де ле ние:

Плот ность ве ро ят но сти :

f x

x x

( )

, ;

< >

< <

0 0 1

1 0 1

если

Функ ция рас пре де ле ния :

F x

x x

( )

< <

0 0

0 1

1 1

если

Дан ное рас пре де ле ние по зво ля ет вы чис лить в яв ном ви де ма те ма -

ти че ское ожи да ние и дисперсию:

Ма те ма ти че ское ожи да ние:

x x p x dx x dx= × = × =

-¥

ò ò

( )

Дис пер сия:

2 2

= - = -

-¥

ò ò

( ) ( )x x p x dx x dx

б) Экс по нен ци аль ное (по ка за тель ное) рас пре де ле ние :

Плот ность ве ро ят но сти:

f x

x x

( )

exp( ),

× - >

l l если

если

0 0

Функ ция рас пре де ле ния:

F x

x x

( )

exp( ),

- - >

1 0

0 0

l если

если

Экс по нен ци аль ный за кон рас пре де ле ния (и толь ко он) об ла да ет

важ ным свой ст вом то го, что ве ро ят ность без от каз ной ра бо ты (на при -

мер, при бо ра) в дан ном ин тер ва ле вре ме ни не за ви сит от вре ме ни пред -

ше ст вую щей ра бо ты, а за ви сит только от длины данного интервала

времени.

в) Би но ми наль ное рас пре де ле ние (фор му ла Бер нул ли):

( )

P C p q

m n m

p q

mn n

m m n m m n m

× -

× ×

- -

! !

Дан ное рас пре де ле ние по ка зы ва ет, что при по втор ных не за ви си -

мых ис пы та ни ях, в ка ж дом из ко то рых мо жет осу ще ст вить ся не ко то рое

со бы тие с од ной и той же ве ро ят но стью, ве ро ят ность лю бо го чис ла его

по яв ле ний со от вет ст ву ет чле нам раз ло же ния би но ма Нью то на в сте пе -

ни рав ной чис лу ис пы та ний.

При мер: мо не та под бра сы ва ет ся 10 раз. Ка ко ва ве ро ят ность то го,

что герб вы па дет 3 раза?

Ре ше ние:

p q= =

P C

3 3 7

0 5 0 5

128

= × × =( , ) ( , )

При

n ® ¥

p ® 0

би но ми аль ное рас пре де ле ние пре вра ща ет ся

в рас пре де ле ние Пу ас со на (пре дель ный слу чай фор му лы Бер нул ли):

W m

( )

= ×

При мер: В кол лек ти ве чис лен но стью 500 че ло век, m лиц ро ди лись

6 ян ва ря. По стро ить рас пре де ле ние этих лиц от 1 до 6.

Ре ше ние: n = 500; p = 1/365; np = 1,37.

m W(m) p

m,500

0 0,2541 0,2537

1 0,3484 0,3484

2 0,2385 0,2388

3 0,0372 0,1089

4 0,0103 0,0372

5 0,0102 0,0101

6 0,0023 0,0023

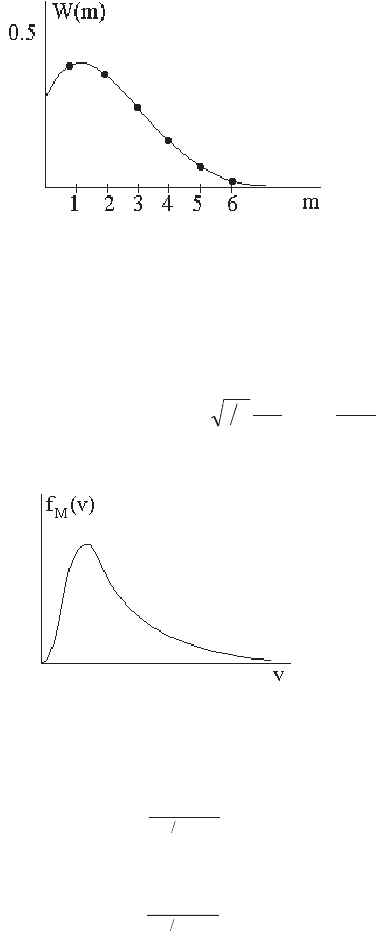
Не труд но ви деть, что в дан ном слу чае (n ®

, p ® 0) оба рас пре -

де ле ния прак ти че ски сов па да ют.

г) В клас си че ской фи зи ке рас пре де ле ние мо ле кул по ско ро стям

опи сы ва ет ся фор му лой Мак свел ла (см. ри су нок 4.7):

Плот ность рас пре де ле ния:

f v

v v

( ) exp( )= -1

a a

где

— па ра метр рас пре де ле ния, боль ший ну ля:

В кван то вой фи зи ке час ти цы с по лу це лым спи ном под чи ня ют ся

рас пре де ле нию Фер ми-Ди ра ка:

E kT

а час ти цы с це лым спи ном — рас пре де ле нию Бо зе-Эйн штей на:

E kT

Рис. 4.6

Рис. 4.7. Рас пре де ле ние Мак свелл ла

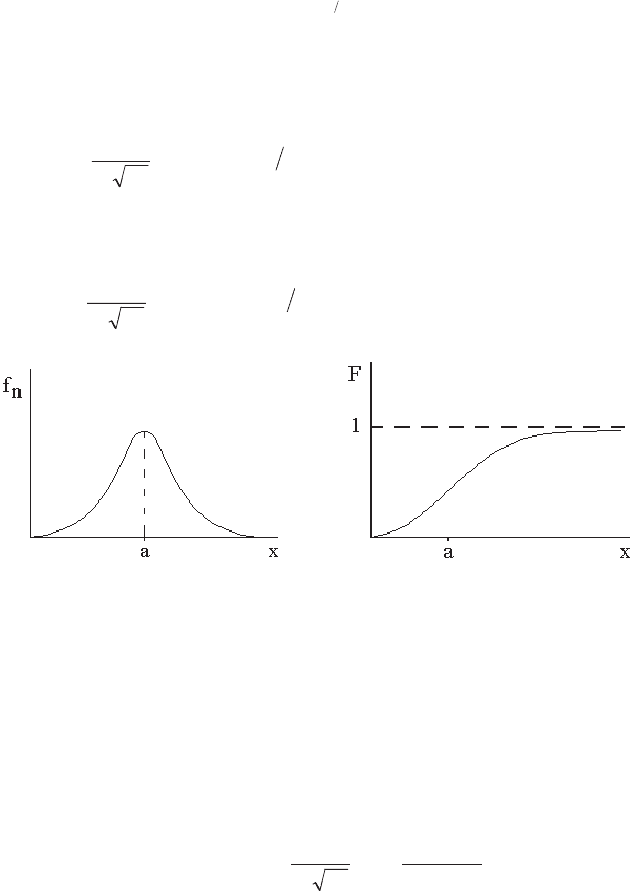
Эти рас пре де ле ния при ус ло вии Е ? кТ пе ре хо дят в клас си че ское

рас пре де ле ние Больц ма на :

n n e

E kT

д) Осо бое зна че ние име ет так на зы вае мое нор маль ное рас пре де -

ле ние слу чай ной ве ли чи ны (рас пре де ле ние Гаусса):

плот ность нор маль но го рас пре де ле ния (см. ри су нок 4.8):

f x

x a b

( ) exp[ ( ) ]=

× - -

2 2

(4.2.8)

ин те граль ная функ ция нор маль но го рас пре де ле ния (см. ри су -

нок 4.9):

F x

x a b dx( ) exp[ ( ) ]=

× - -

-¥

2 2

(4.2.9)

Свой ст ва нор маль но го рас пре де ле ния

Тео ре ма 8. Па ра мет ры a и b в вы ра же ни ях плот но сти ве ро ят но сти

и функ ции рас пре де ле ния слу чай ной ве ли чи ны, рас пре де лен ной по

нор маль но му за ко ну яв ля ют ся ее ма те ма ти че ским ожи да ни ем и дис пер -

си ей.

До ка за тель ст во:

а) Ма те ма ти че ское ожи да ние:

E x x f x dx( ) ( )= ×

-¥

; где

f x

x a

( ) exp

( )

- -

Рис. 4.8

Рис. 4.9

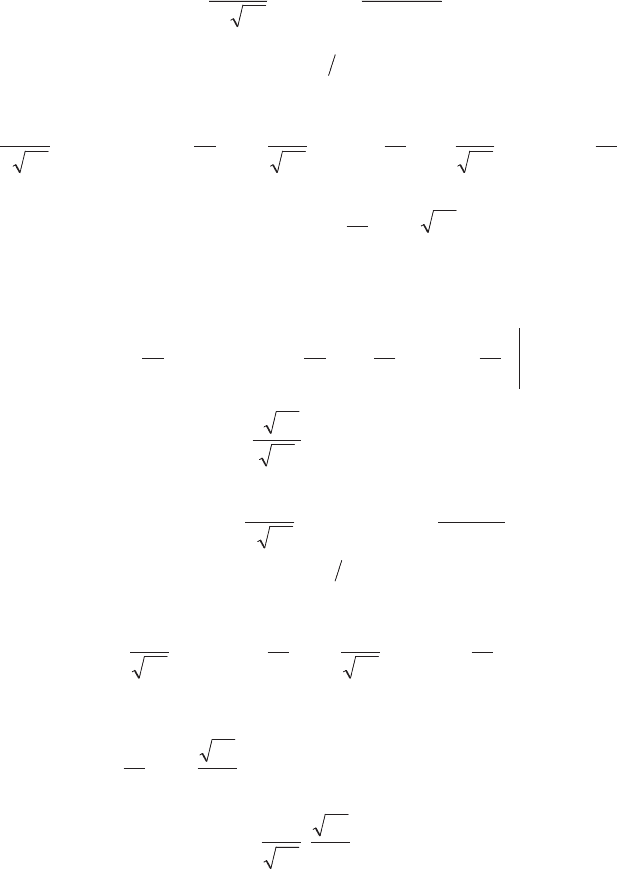
Та ким об ра зом:

E x

x a

dx( ) exp

( )

× ×

- -

-¥

де ла ем за ме ну пе ре мен ной:

t x a b= -( )

;

x t b a= +

;

dx bd t=

, (пре де лы ин -

тег ри ро ва ния не из ме ня ют ся):

= + × -

= -

-¥

a bt

a t

2 2

p p

( ) exp exp

+ × × -

-¥

òò

exp

Здесь пер вое сла гае мое:

exp -

-¥

— ин те грал Эй ле ра-

Пу ас со на.

Вто рое сла гае мое:

× -

= - -

-¥

exp exp

2 2 2

= -

-¥

exp

Та ким об ра зом:

E x

a( ) = =

б) Дис пер сия:

( ) ( ) exp

( )

x a

dx= - -

-¥

cделаем за ме ну пе ре мен ных:

t x a b= -( )

;

x a bt- =

;

dx bd t=

, (пре де лы ин -

тег ри ро ва ния не из ме ня ют ся):

= -

2 2

p p

exp exp

-¥

òò

(так как под ин те гра лом — чет ная функ ция).

exp -

— ин те грал Эй ле ра-Пу ас со на.

Та ким об ра зом:

( )x

b= × =

Что и тре бо ва лось до ка зать.

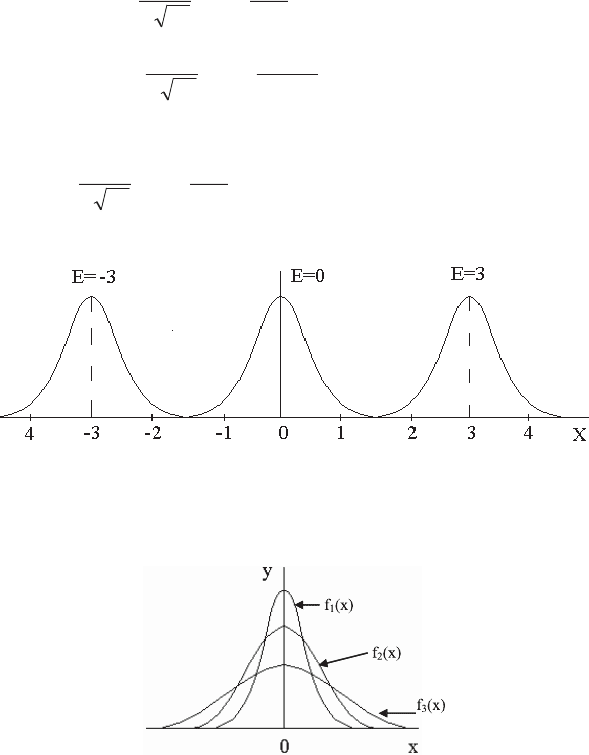
Тео ре ма 9. Слу чай ные ве ли чи ны, рас пре де лен ные по нор маль но -

му за ко ну, раз ли ча ют ся толь ко зна че ния ми ма те ма ти че ско го ожи да ния

и дис пер сии.

До ка за тель ст во:

а) Пусть у двух рас пре де ле ний дис пер сия s

— оди на ко ва, но раз -

ные ма те ма ти че ские ожидания:

E = 0

;

f x

( ) exp= -

s p

;

E ¹ 0

;

f x

x E

( ) exp= -

s p

Ес ли вве сти но вую пе ре мен ную x

= (x – E) , то гда

f x

( ) exp= -

s p

, то есть кри вые для

f x

( )

f x

( )

сов па дут.

Сле до ва тель но, E — это па рал лель ный пе ре нос (ри су нок 4.10):

б) Пусть у трех рас пре де ле ний оди на ко вые ма те ма ти че ские ожи -

да ния E (E = 0), но дис пер сии раз ные: s

= 1/2; s

= 1; s

= 2.

(см. рис. 4.11):

Рис. 4.10

Рис. 4.11

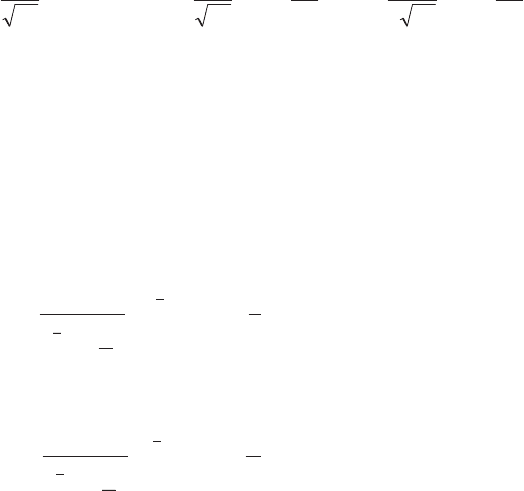
f x

2= -

exp( )

;

= -

exp

;

2 2

= -

exp

Не труд но ви деть, что дис пер сия слу жит ме рой рас сея ния слу чай -

ной ве ли чи ны.

е) В ма те ма ти че ской ста ти сти ке час то ис поль зу ют за ко ны рас -

пре де ле ния слу чай ных ве ли чин, яв ляю щих ся функ ция ми не за ви си -

мых нор маль ных слу чай ных ве ли чин. Впер вые ас тро ном Ф.Хель мерт

(1876 г.) ис сле до вал сум мы квад ра тов нор маль но рас пре де лен ных слу -

чай ных ве ли чин и по лу чил рас пре де ле ние, ко то рое поз же (1900 г.)

К.Пир сон на звал функ ци ей рас пре де ле ния «хи квад рат» (

( )

exp=

× × -

; (4.2.10)

со от вет ст вую щая плот ность ве ро ят но сти:

f x

( ) exp=

× × -

, (4.2.11)

где Г(m) — гам ма-функ ция Эй ле ра:

G( ) exp( )m x x dx

= × -

, (4.2.12)

k — на зы ва ет ся чис лом сте пе ней сво бо ды не за ви си мых нор маль ных

слу чай ных ве ли чин

x x x

, ,...

Рас пре де ле ние

ищет ся для слу чай ных ве ли чин

x x x x

k k

2 2

= + + +K

Оно та бу ли ро ва но (пред став ле но в ви де таб лиц).

Сред нее:

E k

, дис пер сия:

2= k

ж) Анг лий ский ста ти стик В.Гос сет (пи сав ший под псев до ни мом

«Стью дент») по лу чил в 1908 г. для слу чай ных нор маль но рас пре де лен -

ных ве ли чин, так на зы вае мое, «t-рас пре де ле ние»: