Keyfitz N., Caswell H. Applied Mathematical Demography

Подождите немного. Документ загружается.

16.1. Births Averted by Contraception 405

Table 16.1. Birth rates per month with various degrees of contraceptive eﬃciency,

based on p =0.2 without protection, and s =17

p(1−e)

+ s

0.00 0.04545

0.01 0.04535

0.05 0.04492

0.50 0.03704

0.75 0.02703

0.90 0.01493

0.94 0.00997

0.95 0.00855

0.96 0.00704

0.97 0.00544

0.98 0.00375

0.99 0.00193

1.00 0.00000



(e)=−



{[1/p(1 − e)] + s}



p(1 − e)



Thus the additional births averted by a year of increase δ in eﬃciency, as

a fraction of the number that would otherwise have occurred, are

−



(e)δ

f(e)

(1 − e)[1 + sp(1 − e)]

. (16.1.4)

The values of this expression for four values of e and p =0.2,s=17are

as follows:

Further

fraction averted

by improvement δ

e in eﬃciency

00.23δ

0.97.46δ

0.95 17.09δ

0.97 30.25δ

Evidently to go from no protection to a contraceptive of 1 percent eﬃ-

ciency averts only 0.23δ =(0.23)(0.01) = 0.23 percent of births. On the

other hand, to go from a contraceptive of 97 percent eﬃciency to one of

98 percent eﬃciency averts over 30 percent of births. The extra 1 percent

of eﬃciency is 130 times as eﬀective in lowering pre-existing births at the

97 percent level as at the 0 percent level. [Express the relative eﬃciency in

terms of possible births.]

406 16. Microdemography

0.00

0.04545

1.00

Birth rate per month

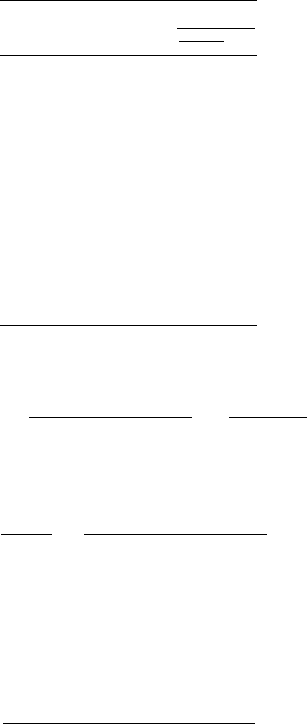
Figure 16.2. Curve of monthly birth rates at various eﬃciencies of contraception,

p =0.2 and s =17months.

Table 16.1 provides both a veriﬁcation of these numbers and an illustra-

tion of their meaning. To go from 0 to 0.01 eﬃciency (a diﬀerence δ =0.01)

decreases the monthly birth rate by 0.04545−0.04535 = 0.00010 on 0.04545,

or 0.0022, which is 0.0022/0.01 or 0.22, and multiplying by δ this is the

same except for rounding as the 0.23δ above. To go from 0.96 to 0.98 ef-

ﬁciency is to lower the birth rate from 0.00704 to 0.00375, a diﬀerence of

0.00329, or 0.00164 per 0.01 of increase in eﬃciency. As a fraction of births

at 0.97 eﬃciency (Table 16.1) this is 0.00164/0.00544 = 0.301, or 30.1δ,

since δ =0.01, in agreement except for slight curvature and rounding with

the 30.25δ given above.

Figure 16.2 shows monthly birth rates as a function of eﬃciency of contra-

ception for the simple model here used. The numbers in the table following

(16.1.4) give the relative slope at four points in the curve.

16.1.3 Dropping the Contraceptive

We have been considering an IUD, a supply of pills, or other “segment,” as

Tietze and Potter call it, of contraception, and have calculated the eﬀect per

year, as though everyone would use the supply according to instructions and

without interruption. But we know that diﬀerent individuals continue to be

careful for diﬀerent lengths of time. A rough way of taking this into account

is to suppose each woman has a probability d of dropping the contraceptive

in each month. During one segment the probability of conception in a given

month is p



(supposed the same for all women and for all times), and the

probability in any month of dropping the contraceptive for the women who

do not become pregnant while using it is d.

All of the above refers to a particular month, and we suppose that the

women are followed through time until they either become pregnant or drop

16.1. Births Averted by Contraception 407

the contraceptive. One of these happening in the ﬁrst month has probability



+ d; its not happening in that month but happening in the next month

has probability (1 − p



− d)(p



+ d); its happening in the third month for

the ﬁrst time has probability (1 −p



−d)



+ d); and so on. If we write q

for 1 − p



− d, the sequence is

(1 − q),q(1 − q),q

(1 − q), ....

The mean number of months of exposure is

(1 − q)+2q(1 − q)+3q

(1 − q)+···=1+q + q

+ ··· =

1 − q

1 − (1 − p



− d)



+ d

before the woman passes out of the group either through becoming pregnant

or dropping the contraceptive.

Among the women who leave the group of nonpregnant contraceptive

users during a particular month, the proportion d/(p



+ d)dosothrough

dropping the contraceptive, and p



/(p



+ d) do so through becoming preg-

nant. If, in each case, this is the fraction in every single month, it is also

the fraction in all months together. Thus d/(p



+ d) of the original group

of women will sooner or later drop the contraceptive and we suppose that

they revert to natural fertility; their chance of conceiving in any month

becomes p. The model follows all women to pregnancy, either while using

the contraceptive or subsequently. With the same argument, now applied

to p rather than to p



+ d, their mean time to pregnancy after dropping the

contraceptive will be 1/p.

Thus all women average 1/(p



+ d) months until they drop the contra-

ceptive or become pregnant; d/(p



+d) of them drop the contraceptive, and

these take another 1/p months, on the average, to become pregnant. Then

the expected time to pregnancy for all of the women is

t =



+ d



+ d





. (16.1.5)

The model for births averted once again consists of comparing two groups

of women, one group initially using the contraceptive and the other never

using it, and following through successive segments. Those initially using

the contraceptive will take an average of t months to become pregnant;

those not using it, an average of 1/p months. Suppose again that the non-

fecund time of childbearing plus the postpartum anovulatory period is s

months for all women, and that we count only pregnancies leading to live

births (i.e., disregarding miscarriages and stillbirths). Then those practic-

ing contraception will average a live birth every t+s months, that is to say,

their monthly birth rate will be 1/(t + s). The group not using the contra-

ceptive will average a birth every (1/p)+s months, and the corresponding

rate is 1/[(1/p)+s]. The problem is now solved: the reduction in monthly

408 16. Microdemography

birth rates due to the contraceptive is the diﬀerence

(1/p)+s

−

t + s

and as a fraction of the birth rate without the contraceptive this reduces

1 −

(1/p)+s

t + s

. (16.1.6)

If an IUD is 95 percent eﬃcient and is inserted in each of a group of

women of natural fertility with p =0.2 chance of a pregnancy leading to

a live birth each month, so that for protected women the chance of an

accidental pregnancy is 0.01 each month, and if the chance of a woman’s

dropping the contraceptive and reverting to natural fertility in any given

month is d =0.03, and if the nonfecund period of pregnancy and its after-

math is s = 17 months, then t =28.75 months. Expression 16.1.6 says that

users of the method avert 0.52 of the births that would otherwise occur.

But we should take account of the fact that women do not ordinarily

go directly from natural fertility to modern contraception. The recruits to

an IUD program have ordinarily been restricting their births in one way

or another. Suppose that they have been practicing rhythm with care and

attaining 90 percent eﬃciency, so that the chance of childbearing if they

did not have the IUD is p =0.02,anditistothispracticethattheyrevert

if they drop the IUD. Then t =62.5; and, entering p =0.02 in place of

p =0.2 in (16.1.6), we ﬁnd the fraction of births averted to be 0.16 rather

than 0.52 as in the preceding paragraph.

The above argument, due to Potter (1970), illustrates once more the

general point of causal inference that nothing can be said about the eﬀect

of the IUD without specifying what the couples concerned would be doing

without it. That such speciﬁcation is important appears from our numbers:

with natural fertility as the alternative to the IUD 52 percent of births are

averted, whereas with 90 percent eﬃcient contraception in the background

only 16 percent are averted.

The above argument emerges in the simplest possible form when we try

to see the eﬀect of abortion on the birth rate.

16.1.4 Why 1000 Abortions Do Not Prevent 1000 Births

in a Population

That the logic of individuals becomes grossly misleading when applied

to populations is implicit in much of the work in this book. The contrast

between individuals and populations is especially sharp in regard to births

averted by abortion. If we think of a woman aborting a pregnancy that

would have led to a live birth, then one abortion has indeed prevented one

birth. But 1000 abortions in a population generally prevent far fewer than

16.1. Births Averted by Contraception 409

1000 births. To ﬁnd how many they do prevent we must reckon in terms of

each woman’s time—how long she takes to have a birth, how long she is tied

up in having an abortion. Once again only conceptions potentially leading

to live births will be considered, that is to say, spontaneous abortions will

be disregarded (Potter 1972).

A woman who has just conceived may decide to have an abortion in

the second month and be sterile for 1 further month, a total time from

conception of 3 months. Suppose that she is then fecund again, with the

same probability 0.2 of conceiving in each month without contraceptive

protection. To arrive at this point from the last previous fecund condition

has taken her the 3 infertile months before and after the abortion, plus the

preceding expected 5 months to pregnancy, 8 months in all. The 8 months

represent the time out from childbearing due to one abortion. Only if this

length of time were suﬃcient to have a child would one abortion prevent

one birth in the population. If the cycle for having a child is 22 months on

the average, as in this illustration, the abortion has prevented only 8/22 of

a birth. On these assumptions nearly three abortions are required to avert

one birth.

More generally, we can see how many births are prevented by abortions

taking place at such time after the onset of pregnancy that the woman is

infecund for an expected a months. The length of the cycle involving one

abortion averages (1/p)+a, and the length of the cycle involving one birth

averages (1/p)+s; the number of the former that will ﬁt into the latter is

(1/p)+s

(1/p)+a

. (16.1.7)

This being the number of abortion cycles required to ﬁll the time that will

be taken by one birth cycle, it is also the number of abortions that will pre-

vent one birth. The model is deterministic; it compares two women going

through repeated cycles, one involving births and the other involving abor-

tions, without allowing for variation in the length of cycle or in fecundity

among women.

16.1.5 Abortion as a Backup to Contraception

Expression 16.1.7 refers to a population that does not use contraception. In

populations that do practice birth control, the fractional eﬀect of abortion

is much greater, and (16.1.7) can be readily modiﬁed to show how much.

To apply the argument to our new problem we write p(1 − e)inplace

of p as the probability of conceiving in a particular month and again go

through the whole of the preceding argument. The mean length of time

to pregnancy for fertile couples becomes 1/p(1 − e), and the number of

410 16. Microdemography

abortions that will prevent one birth is now

1/p(1 − e)

+ s

1/p(1 − e)

+ a

. (16.1.8)

Entering p =0.2, e =0.95, s = 17 months, and a = 3 months gives

(1/0.01) + 17

(1/0.01) + 3

117

103

=1.14

abortions to prevent one birth.

This is a very diﬀerent outcome from the no-contraception case. With

unprotected intercourse nearly three abortions are required to prevent one

birth. With 95 percent eﬃcient contraception only about one and one-

seventh abortions are needed to prevent one birth. If the eﬃciency of

contraception were higher than 0.95, an abortion would have even more

impact.

Although this section has used the length of the conception and birth cy-

cle to obtain birth rate in the context of contraceptive eﬀects, it is relevant

in many other contexts. The interval between births is an important pa-

rameter in such species as whales (e.g., Barlow and Clapham 1997, Caswell

et al. 1999), elephants (Wu and Botkin 1980, Moss 2001), and the great

albatrosses (e.g., Croxall et al. 1990). This interval may change in response

to environmental factors, and the result can be used to project their impact

on the population (Caswell et al. 1999).

The absorbing Markov chain approach of Chapter 11 can be used to

calculate the interbirth interval in complex stage-classiﬁed life cycles if

reproducing females are identiﬁed as a stage (Fujiwara and Caswell 2001,

Fujiwara et al. 2004). The approach is to make reproduction an absorbing

state and calculate the mean time to absorption in a chain conditional on

reaching that state before death (see Section 11.1.2.2). It could be applied

directly to matrix versions of multistate models of fertility, such as those

of Wood et al. (1994) or Yashin et al. (1998).

16.2 Measurement of Fertility and Fecundity

According to the usual English language deﬁnitions, fecundity is the unin-

hibited biological capacity of women to bear children; fertility is the number

of children borne under existing social conditions. Fertility is fecundity

modiﬁed by contraception and other kinds of intervention. (Ecologists often

switch the deﬁnitions.)

Fertility is directly measurable—the birth of a child is a publicly rec-

ognized event, and its recording is merely a matter of organization and

attention, especially by those, parents and doctors, who are in a position

to observe the event as it occurs and so have the necessary facts about it.

16.2. Measurement of Fecundity 411

But the underlying fecundity depends on decidedly private circumstances

not generally known even to the couples concerned. These include viability

of sperm and ovum as this aﬀects the length of the fertile period, and other

factors hidden from direct observation. The problem of measuring these

and their inﬂuences on the birth rate will be the subject of this section.

16.2.1 Probability of Conception by Days of the Month

A rough way of calculating probability of conception, making use only of

the frequency of intercourse and the length of the fertile period, is implied

in the work of Glass and Grebenik (1954). Suppose that a couple have

intercourse n times in the menstrual cycle, which includes a fertile period

of f days out of a total of 25 nonmenstruating days per month. Then if

coitus is unplanned in relation to the fertile period, the probability that it

will occur at least once during the f fertile days is the complement of the

probability that it will not occur at all during those days: the chance that

any particular coitus will take place during the nonfertile period is 1−f/25.

If diﬀerent occurrences of intercourse are independently random, with no

spacing, the chance that all n will take place during the nonfertile period

is this quantity to the nth power: (1 − f/25)

.Thechancep that at least

one coitus will take place during the fertile period must be the complement

of this last:

p =1−



1 −



and if ovum and sperm are healthy and behave as expected, this is the

chance of conception during the month in question.

For a given n the probability is increased insofar as there is a degree of

regularity in intercourse, for instance, if it occurs only once in each 24-hour

period (Jain 1969). Divide the nonmenstruating part of the month into 25

separate days, each a 24-hour interval, and suppose that in f of these the

woman is fertile; then the chance of avoiding the ﬁrst of the f days with

coitus on n (separate) random days is 1 −n/25. The chance of avoiding all

f days with n acts of coitus spread over diﬀerent days is (1 − n/25)

,and

hence the chance of conception is

p =1−



1 −



We need to allow not only for frequency of intercourse but also for the

moment when intercourse occurs in relation to the moment of ovulation,

using the best knowledge or guesses regarding the probability of conception

for intercourse on the day of ovulation, 1 day earlier, 2 days earlier, or

1 day later. Lachenbruch (1967) set up a model that incorporates these

probabilities and simulated it by computer to obtain numerical results.

For couples using rhythm as a means of contraception and having their

412 16. Microdemography

intercourse in two “humps,” one before and one after ovulation, he found

probabilities of conception of 0.07 to 0.20, and commented that the time

he allowed for intercourse would be too short for most couples. “Bracketed

rhythm,” in which the couple have intercourse on the last “safe” day before

ovulation and the ﬁrst “safe” day after, leads to a fairly high value of the

probability of conception—0.20 with the assumptions made. A feature of

bracketed intercourse is that the total frequency of intercourse has almost

no eﬀect on conception.

To estimate probabilities on conception on the several days of the cycle,

Barrett and Marshall (1969) followed 241 fertile British couples, mostly

20 to 40 years of age and not using birth control. They obtained from

each couple each month a calendar showing dates of intercourse, and a

temperature chart from whose rise at midmonth the time of ovulation could

be read. Then, if p

is the probability that intercourse on the ith day will

lead to conception, the chance 1 − p that conception did not occur during

a particular month must be the product

1 − p =

(1 − p

)

taken over the days of the month, where x

is 1 if intercourse took place

on the ith day and 0 if it did not.

One would like to ﬁnd values of p

such that the above product for 1 −p

comes as close as possible to 1 for the months when conception did not

occur, and to 0 for the months when it did. Barrett and Marshall took the

logarithm of the likelihood and maximized for the whole sample of cycles.

Their estimates for the 5 days before ovulation and the 1 day after it were

as follows:

−4.5

0.13

−3.5

0.20

−2.5

0.17

−1.5

0.30

−0.5

0.14

0.5

0.07

Thus the highest probability of conception, 0.30, was for the day 24 to 48

hours before ovulation. Outside of the above 6-day range the probabilities

were not signiﬁcantly diﬀerent from zero.

From these numbers it follows that daily intercourse gives a probability

of conception

p =1− (1 − 0.13)(1 − 0.20) ···=0.68.

The probability is 0.43 for intercourse every second day, 0.31 for every third

day, and 0.24 for every fourth day (numbers rounded after calculation, and

16.2. Measurement of Fecundity 413

without making allowance for the eﬀect of frequency of intercourse on the

production of sperm).

16.2.2 Mean Fecundity from Surveys

The probability p of conceiving in a given month for a group of fertile

women is typically sought in order to compare it with p



, the corresponding

ratio for another group of women. When p applies to women not practicing

contraception, it is an estimate of fecundity or natural fertility; the amount

by which p



, for a group of women practicing contraception, is lower mea-

sures the eﬃciency of that form of contraception. The most obvious way of

obtaining estimates is by observing waiting times until pregnancy, a sub-

ject to which we proceed.

Homogeneous Populations. The measurement of fertility, either natural or

with contraceptive protection, depends on data for a group of women all

of whom are having intercourse and are nonpregnant; suppose all to be

subject to the same probability p of conceiving in each month, where p is

greater than zero. Suppose that N fertile women, just married, are surveyed

month by month until they become pregnant; as each becomes pregnant,

she drops out of observation. Let the number who become pregnant in

the ﬁrst month be N

, the number who become pregnant in the second

month N

, and so on. Then the probability of conception in any month,

p, is estimated from the ﬁrst month’s data as the ratio N

/N .Thisleaves

N − N

women starting the second month in a fecund condition, and the

estimate of p from that month’s data is the ratio N

/(N −N

), and similarly

for later months. A series of estimates of p is thus provided

ˆp

N − N

ˆp

N − N

− N

ˆp

N − N

− N

−···−N

m−1

where observation stops after the mth month.

To make use of all the information we must average the several values

of ˆp

, ˆp

,.... If the true probability p is the same for all women and for

all months, the right average is one that weights the several months by

their sample sizes: we need to weight our ˆp

, ˆp

,...,ˆp

by the number of

exposed women on which each is based. Since ˆp

is based on N women, ˆp

414 16. Microdemography

on N − N

, and so on, the estimate is

N ˆp

+(N − N

)ˆp

+ ···+(N − N

− N

−···−N

m−1

)ˆp

N +(N − N

)+···+(N − N

− N

−···−N

m−1

)

or, entering the estimates ˆp

, ˆp

,... from above,

+ N

+ ···+ N

N +(N − N

)+···+(N − N

− N

−···−N

m−1

)

, (16.2.1)

supposing that all women are followed to the mth month.

This widely used index, due to Pearl (1939, p. 296), will be referred to

as ˆp

. It contains the total number of conceptions during the m months of

observation in its numerator, and its denominator is the number of woman-

months of exposure, if the month of conception is counted into the exposure.

The index is intuitively appealing quite apart from the statistical argument

above. Multiplied by 1200, it gives pregnancies per 100 woman-years of in-

tercourse, and this rate is often calculated and published. Not only does ˆp

seem intuitively reasonable, but also, if all women were equally susceptible,

it would be the correct measure, and we would need to go no further in the

search for a measure of fecundity.

A Heterogeneous Population with Fecundity Constant for Each Woman.

However, we know that some women are more fecund than others, and

we seek from the survey a suitable average of their several p values. The

women who are most fecund will tend to become pregnant ﬁrst, so the

ˆp

, ˆp

,... for the several months are estimating diﬀerent quantities. The

estimate for the ﬁrst month ˆp

= N

/N , refers to unselected women and

is an unbiased estimate of the mean p. Since those who become pregnant

drop out of observation, no later month refers to unselected women. The

ith month, for any i>1, omits some women selected for their fecundity,

and so the estimate derived from it, N

/(N −N

−N

−···−N

i−1

), must

be an underestimate of the fecundity of the original N women.

The p values diﬀered from month to month in the sample size on which

they were estimated in the model underlying p

, and they diﬀered in no

other way. With such homogeneous material the correct way to weight a

number of estimates of the same parameter is by the quantity of informa-

tion contained in each estimate, that is, by the size of sample available in

each month. With heterogeneity among women the pregnancy ratios are

genuinely diﬀerent in the diﬀerent months, and to weight by the quantity of

information, that is, the sample size, would be incorrect. To avoid consid-

ering two diﬀerent problems at once we will now suppose that the sample

is large, so that random variation can be disregarded. What is wanted is a

population average, in which each woman counts once, and hence we must

weight the women of a given fecundity class according to the number of

women in that class in the population. (See Chapter 19 for a more general

discussion of heterogeneity.)