King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

In the golden section search method, once a bracketing interval is identiﬁed (for

now, assume that the initial bracketing interval has length ab equal to one), two

points x

and x

in the interval are chosen such that they are positioned at a distance

equal to ð1  rÞ from the two ends. Thus , the two interior points are symmetrically

located in the interval (see Figure 8.7).

Because this is the ﬁrst iteration, the function is evaluated at both interior points.

A subinterval that brackets the minimum is selected using the algorithm discussed

above. If fx

ðÞ

ðÞ, interval x

; b½is selec ted. On the other hand, if fx

ðÞ

ðÞ,

interval a; x

½is selected. Regardless of the subinterval selected, the width of the new

bracket is r. Thus, the interval has been reduced by the fraction r.

The single interior point in the chosen subinterval divides the new bracket

according to the golden ratio. This is illustrated next. Suppose the subinterval

; b½is selected. Then x

divides the new bracket according to the ratio

1  r

;

which is equal to the golden ratio (see Equation (8.5)). Note that x

b is the longer

segment of the line x

b, and x

b is a golden section. Therefore, we have

Therefore, one interior point that divides the interval according to the golden ratio is

already determined. For the next step, we need to ﬁnd only one other point x

in the

interval x

; b½such that

1  r

This is illustrated in Figure 8.8.

The function is evaluated at x

and compared with fx

ðÞ. Depending on the

outcome of the comparison, either segment x

or segment x

b is discarded. The

width of the new interval is 1 – r, which is equal to r

. Thus, the interval x

; b½of

length r has been reduced to a smaller interval by the fraction r. Thus, at every step,

the interval size that brackets the minimum is reduced by the fraction r = 0.618.

Since each iteration discards 38.2% of the current interval, 61.8% of the error in the

estimation of the minimum is retained in each iteration. The ratio of the errors of two

consecutive iterations is

iþ1

¼ 0:618:

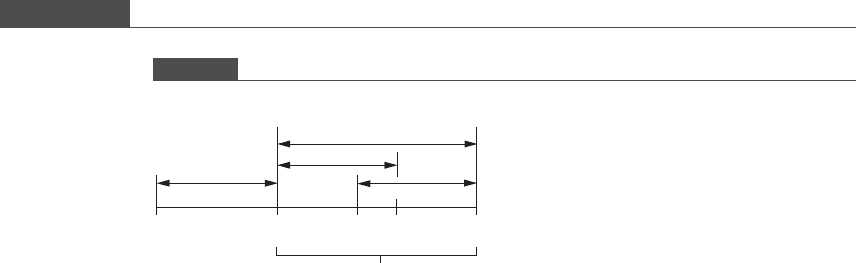
Figure 8.7

First iteration of the golden section search method

1 − r

1 – r

497

8.2 Unconstrained single-variable optimization

Comparing the above expression with Equation (5.10), we ﬁnd r = 1 and C = 0.618.

The convergence rate of this method is therefore linear. The interval reduction step is

repeated until the width of the bracket falls below the tolerance limit.

Algorithm for the golden section search method

(1) Choose an initial interval ½a; b that brackets the minimum point of the unimodal

function and evaluate fðaÞ and fðbÞ.

(2) Calculate two points x

and x

such that x

¼ 1  rðÞðb  aÞþa and

¼ rðb  aÞþa, where r ¼ð

ﬃﬃﬃ

 1Þ=2 and b  a is the width of the interval.

(3) Evaluate fx

ðÞand fx

ðÞ.

(4) The function values are compared to determine which subinterval to retain.

(a) If fx

ðÞ

ðÞ, then the subinterval ½x

; b is chosen. Set a ¼ x

; x

¼ x

;

faðÞ¼fx

ðÞ; fx

ðÞ¼fx

ðÞ; and calculate x

¼ rðb  aÞþa and fx

ðÞ.

(b) If fx

ðÞ

ðÞ, then the subinterval ½a; x

 is chosen. Set b ¼ x

; x

¼ x

;

fbðÞ¼fx

ðÞ; fx

ðÞ¼fx

ðÞ; and ﬁnd x

¼ 1  rðÞðb  aÞþa and fx

ðÞ.

(5) Repeat step (4) until the size of the interval is less than the tolerance speciﬁcation.

Another bracketing method that requires the determination of only one new

interior point at each step is the Fibonacci search method. In this method, the

fraction by which the interval is reduced varies at each stage. The advantage of

bracketing methods is that they are much less likely to fail compared to deriva tive-

based methods, when the derivative of the function does not exist at one or more

points at or near the extreme point. Also, if there are points of inﬂection located

within the interval, in addition to the single extremum, these will not inﬂuence the

search result of a bracketing method. On the other hand, Newton’s method is

likely to converge to a point of inﬂection, if it is located near the initial guess

value.

Using MATLAB

The MATLAB software contains the function fminbnd, which performs minimi-

zation of a nonlinear function in a single variable within a user-speciﬁed interval

(also termed as bound). In other words, fminbnd carries out bounded single-

variable optimization by minimizing the objective function supplied in the function

call. The minimization algorithm is a combinat ion of the golden section search

method and the parabolic interpolation method. The syntax is

Figure 8.8

Second iteration of the golden section search method

1 − r

New bracket

498

Nonlinear model regression and optimization

x = fminbnd(func, x1, x2)

[x, f] = fminbnd(func, x1, x2)

func is the handle to the function that calculates the value of the objective

function at a single value of x; x

and x

specify the endpoints of the interval

within which the optimum value of x is sought. The function output is the value of

x that minimi zes fu nc, and, optionally, the value of the objective function at x.An

alternate syntax is

x = fminbnd(func, x1, x2, options)

options is a structure that is created using the optimset function. You can set the

tolerance for x, the maximum number of function evaluations, the maximum

number of iterations, and other features of the optimizat ion procedure using

optimset. The default tolerance limit is 0.0001 on a change in x and fðxÞ. You

can use optimset to choose the display mode of the result. If you want to display

the optimization result of each iteration, create the options structure using the

syntax below.

options = optimset(‘Display’, ‘ iter’)

Box 8.2C Optimization of a fermentation process: maximization of profit

We solve the optimization problem discussed in Box 8.2A using the golden section search method.

MATLAB program 8.5 (listed below) minimizes a single-variable objective function using this method.

MATLAB program 8.5

function goldensectionsearch(func, ab, tolx)

% The golden section search method is used to ﬁnd the minimum of a

% unimodal function.

% Input variables

% func: nonlinear function to be minimized

% ab : bracketing interval [a, b]

% tolx: tolerance for estimating the minimum

% Other variables

r = (sqrt(5) - 1) /2; % interval reduction ratio

k = 0; % counter

% Bracketing interval

a = ab(1);

b = ab(2);

fa = feval(func, a);

fb = feval(func, b);

% Interior points

x1 = (1 - r)*(b - a) + a;

499

8.2 Unconstrained single-variable optimization

8.3 Unconstrained multivariable optimization

In this section, we focus on the minimization of an objective function fðxÞof n variables,

where x ¼ x

; x

; ...; x

½.IffðxÞis a smooth and continuous function such that its ﬁrst

x2 = r*(b - a) + a;

fx1 = feval(func, x1);

fx2 = feval(func, x2);

% Iterative solution

while (b - a) > tolx

if fx1 > fx2

a = x1; % shifting interval left end-point to the right

fa = fx1;

x1 = x2;

fx1 = fx2;

x2 = r*(b - a) + a;

fx2 = feval(func, x2);

else

b = x2; % shifting interval right end-point to the left

fb = fx2;

x2 = x1;

fx2 = fx1;

x1 = (1 - r)*(b - a) + a;

fx1 = feval(func, x1);

end

k=k+1;

end

fprintf(‘a = %7.6f b = %7.6f f(a) = %7.6f f(b) = %7.6f \n’, a, b, fa, fb)

fprintf(‘number of iterations = %2d \n’,k)

goldensectionsearch(‘proﬁtfunction’,[50 70], 0.01)

a = 59.451781 b = 59.460843 f(a) = -19195305.961470 f(b) =

-19195305.971921

number of iterations = 16

Finally, we demonstrate the use of fminbnd to determine the optimum value of the flowrate:

x = fminbnd(‘proﬁtfunction’, 50, 70,optimset(‘Display’,‘iter’))

Func-count x f(x) Procedure

1 57.6393 -1.91901e+007 initial

2 62.3607 -1.91828e+007 golden

3 54.7214 -1.91585e+007 golden

4 59.5251 -1.91953e+007 parabolic

5 59.4921 -1.91953e+007 parabolic

6 59.458 -1.91953e+007 parabolic

7 59.4567 -1.91953e+007 parabolic

8 59.4567 -1.91953e+007 parabolic

9 59.4567 -1.91953e+007 parabolic

Optimization terminated:

the current x satisﬁes the termination criteria using OPTIONS.TolX of

1.000000e-004

59.4567

500

Nonlinear model regression and optimization

derivatives with respect to each of the n variables exist, then the gradient of the function,

rf xðÞ, exists and is equal to a vector of partial derivatives as follows:

rf xðÞ¼

∂f

∂x

∂f

∂x

∂f

∂x

: (8:6)

The gradient vector evaluated at x

, points in the direction of the largest rate of

increase in the function at that point. The negative of the gradient vector rf x

ðÞ

points in the direction of the greatest rate of decrease in the function at x

. The

gradient vector plays a very important role in derivative-based minimization algo-

rithms since it provides a search direction at each iteration for ﬁnding the next

approximation of the minimum.

If the gradient of the function fðxÞ at any point x* is a zero vector (all components

of the gradient vector are equal to zero), then x* is a critical point. If fðxÞf x



ðÞfor

all x in the vicinity of x*, then x* is a local minimum. If fðxÞf x



ðÞ, for all x in the

neighborhood of x*, then x* is a local maximum. If x* is neither a minimum nor a

maximum point, then it is called a saddle point (similar to the inﬂection point of a

single-variable nonlinear function).

The nature of the critical point can be established by evaluating the matrix of

second partial derivatives of the nonlinear objective function, which is called the

Hessian matrix. If the second partial derivatives ∂

f=∂x

∂x

of the function exist for

all paired combinations i, j of the variables, where i, j =1,2, ..., n, then the Hessian

matrix of the function is deﬁned as

HxðÞ¼

∂

∂x

∂

∂x

...

∂

∂x

∂

∂x

∂

∂x

...

∂

∂x

∂

∂x

∂

∂x

...

∂

∂x

: (8:7)

The Hessian matrix of a multivariable function is analogous to the second derivative

of a single-variable function. It can also be viewed as the Jacobian of the gradient

vector rfðxÞ. (See Section 5.7 for a deﬁnition of the Jacobian of a system of

functions.) HxðÞis a symmetric matrix, i.e. a

¼ a

, where a

is the element from

the ith row and the jth column of the matrix.

A critical point x* is a local minimum if Hx



ðÞis positive deﬁnite. A matrix A is

said to be positive deﬁnite if A is symmetric and x

0 for all non-zero vectors x.

Note the following properties of a positive deﬁnite matrix.

(1) The eigenvalues λ

(i =1,2, ..., n) of a positive deﬁnite matrix are all positive.

Remember that an eigenvalue is a scalar quantity that satisﬁes the matrix equation

A  lI ¼ 0. A positive deﬁnite matrix of size n

n has n distinct real eigenvalues.

(2) All elements along the main diagonal of a positive deﬁnite matrix are positive.

The T superscript represents a transpose operation on the vector or matrix.

501

8.3 Unconstrained multivariable optimization

(3) The determinant of each leading principal minor is positive. A principal minor of

order j is a minor obtained by deleting from an n

n square matrix, n – j pairs of rows

and columns that intersect on the main diagonal (see the deﬁnition of a minor in

Section 2.2.6). In other words, the index numbers of the rows deleted are the same as

the index numbers of the columns deleted. A leading principal minor of order j is a

principal minor of order j that contains the ﬁrst j rows an d j columns of the n × n

square matrix. A 3 × 3 matrix has three principal minors of order 2:



;



;



Of these, the ﬁrst principal minor is the leading principal minor of order 2 since it

contains the ﬁrst two rows and columns of the matrix. An n × n square matrix has n

leading principal minors. Can you list the three leading principal minors of a 3 × 3

matrix?

To ascertain the positive deﬁniteness of a matrix, one needs to show that either the

ﬁrst property in the list above is true or that both properties (2) and (3) hold true

simultaneously.

A critical point x* is a local maximum if Hx



ðÞis negative deﬁnite. A matrix A is

said to be negative deﬁnite if A is symmetric and x

0 for all non-zero vectors x.

A negative deﬁnite matrix has negative eigenvalues, diagonal elements that are all

less than zero, and leading principal minors that all have a negative determinant. In

contrast, at a saddle point, the Hessian matrix is neither positive deﬁnite nor

negative deﬁnite.

A variety of search methods for unconstrained multidimensional optimization

problems have been developed. The general procedure of most multivariable opti-

mization methods is to (1) determine a search direction and (2) ﬁnd the minimum

value of the function along the line that passes through the current point and runs

parallel to the search direction. Derivative-based methods for multivariable mini-

mization are called indirect search methods because the analytical form (or numerical

form) of the partial derivatives of the function must be determined and evaluated at

the initial guessed values before the numerical step can be applied. In this section we

present two indirect methods of optimization: the steepest descent method

(Section 8.3.1) and Newton’s method for multidimensional search (Section 8.3.2).

The latter algorithm requires calculation of the ﬁrst and second partial derivatives of

the objective function at each step, while the former requires evaluation of only the

ﬁrst partial derivatives of the function at the approximation x

to provide a new

search direction at each step. In Section 8.3.3, the simplex method based on the

Nelder–Mead algorithm is discussed. This is a direct search method that evaluates

only the function to proceed towards the minimum.

8.3.1 Steepest descent or gradient method

In the steepest descent method, the negative of the gradient vector evaluated at x

provides the search direction at x. The negative of the gradient vector points in the

directionofthelargestrateofdecreaseoffðxÞ. If the ﬁrst guessed point is x

ð0Þ

,thenext

point x

ð1Þ

lies on the line x

ð0Þ

 αrf x

ð0Þ



,whereα is the step size taken in the search

direction from x

ð0Þ

. A minimization search is carried out to locate a point on this line

where the function has the least value. This type of one-dimensional search is called a

line search and involves the optimization of a single variable α. The next point is given by

502

Nonlinear model regression and optimization

ð1Þ

¼ x

ð0Þ

 αrf x

ð0Þ



: (8:8)

In Equation (8.8) the second term on the right-hand side is the incremental step

taken, or Δx ¼αrf x

ð0Þ



. Once the new point x

ð1Þ

is obtained, a new search

direction is calculated by evaluating the gradient vector at x

ð1Þ

. The search pro-

gresses along this new direction, and stops when α

opt

is found, which minimizes the

function value along the second search line. The function value at the new point

should be less than the function value at the previous point, or f x

ð2Þ



f x

ð1Þ



and

f x

ð1Þ



f x

ð0Þ



. This procedure continues iteratively until the partial derivatives of

the function are all very close to zero and/or the distance between two consecutive

points is less than the tolerance limit . When these criteria are fulﬁlled, a local

minimum of the function has been reached.

Algorithm for the method of steepest descent

(1) Choose an initial point x

ðkÞ

. In the ﬁrst iteration, the initial guessed point is x

ð0Þ

(2) Determine the analytical form (or numerical value using ﬁnite differences, a topic

that is brieﬂy discussed in Section 1.6.3) of the partial derivatives of the function.

(3) Evaluate rf xðÞat x

ðkÞ

. This provides the search direction s

ðkÞ

(4) Perform a single-variable optimization to minimize f x

ðkÞ

þ αs

ðkÞ



using any of the

one-dimensional minimization methods discussed in Section 8.2.

(5) Calculate the new point x

ðkþ1Þ

¼ x

ðkÞ

þ αs

ðkÞ

(6) Repeat steps (3)–(5) until the procedure has converged upon the minimum value.

Since the method searches for a critical point, it is possible that the iteratio ns may

converge upon a saddle point. Therefore, it is important to verif y the nature of the

critical point by conﬁrming whether the Hessian matrix evaluated at the ﬁnal point is

positive or negative deﬁnite .

An advantage of the steepest descent method is that a good initial approximation

to the minimum is not required for this method to proceed towards a critical point.

However, a drawback of this method is that the step size in each subsequent search

direction becomes smaller as the minimum is approached. As a result, many steps are

usually required to reach the minimum, and the rate of convergence slows down as

the minimum point nears.

There are a number of varian ts to the steepest descent method that differ in the

technique employed to obtain the search direction, such as the conjugate gradient

method and Powell’s method. These methods are discussed in Edgar and

Himmelblau (1988).

Example 8.1

Using the steepest descent method, find the values of x and y that minimize the function

fx; yðÞ¼x  e

xþy

þ y

: (8:9)

To get a clearer picture of the behavior of the function, we draw a contour plot in MATLAB. This

two-dimensional graph displays a number of contour levels of the function on an x–y plot. Each contour

line is assigned a color according to a coloring scheme such that one end of the color spectrum

(red) is associated with large values of the function and the other end of the color spectrum (blue) is

associated with the smallest values of the function observed in the plot. A contour plot is a convenient

tool that can be used to locate valleys (minima), peaks (maxima), and saddle points in the variable space

of a two-dimensional nonlinear function.

503

8.3 Unconstrained multivariable optimization

To make a contour plot, you first need to create two matrices that contain the values of each of the

two independent variables to be plotted. To construct these matrices, you use the meshgrid function,

which creates two matrices, one for x and one for y, such that the corresponding elements of each

matrix represent one point on the two-dimensional map. The MATLAB function contour plots the

contour map of the function. Program 8.6 shows how to create a contour plot for the function given in

Equation (8.9) .

MATLAB program 8.6

% Plots the contour map of the function x*exp(x + y) + y^2

[x, y] = meshgrid(-3:0.1:0, -2:0.1:4);

z = x.*exp(x + y) + y.^2;

contour(x, y, z, 100);

set(gca, ‘Line Width’,2,‘Font Size’,16)

xlabel(‘x’,‘Fontsize’,16)

ylabel(‘y’,‘Fontsize’,16)

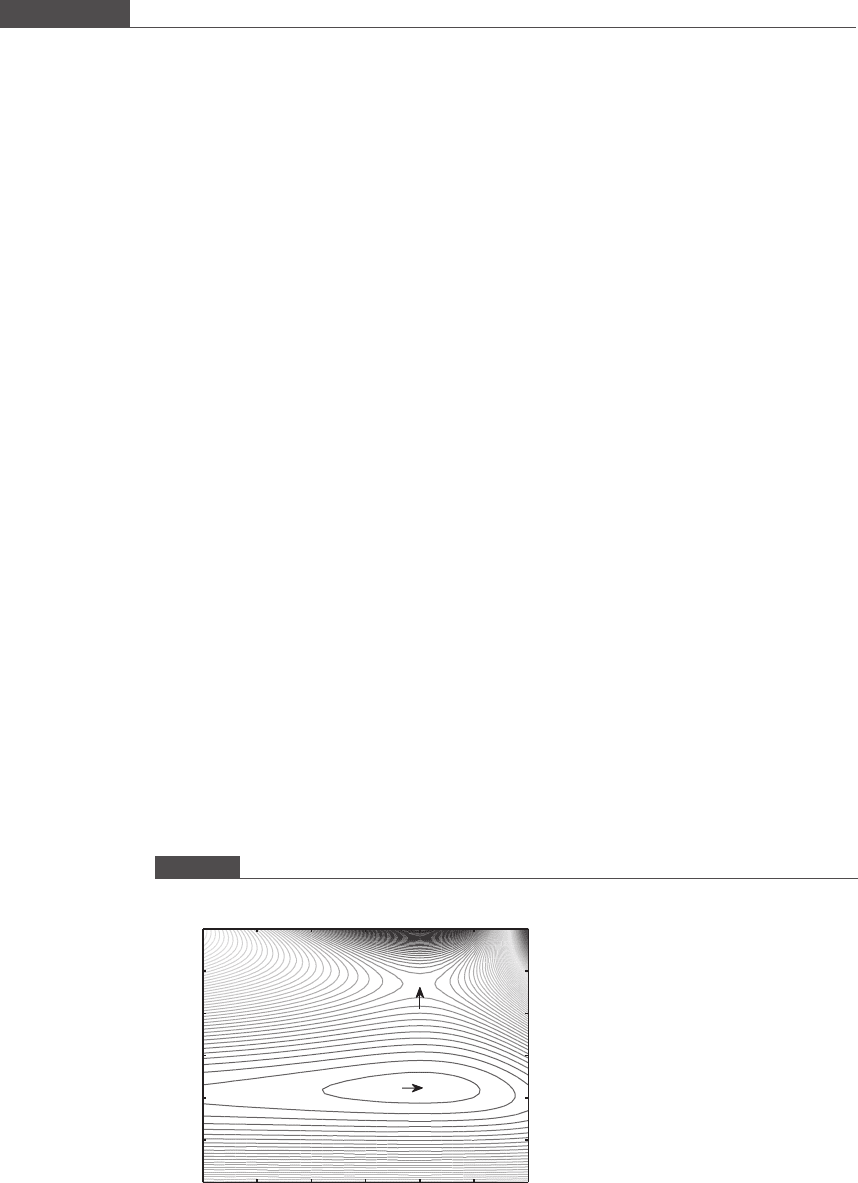
Figure 8.9 is the contour plot created by Program 8.6, with text labels added. In the variable space that

we have chosen, there are two critical points, of which one is a saddle point. The other critical point is a

minimum. We can label the contours using the clabel function. Accordingly, Program 8.6 is modified

slightly, as shown below in Program 8.7.

MATLAB program 8.7

% Plots a contour plot of the function x*exp(x + y) + y^2 with labels.

[x, y] = meshgrid(-3:0.1:0, -1:0.1:1.5);

z = x.*exp(x + y) + y.^2;

[c, h] = contour(x, y, z, 15);

clabel(c, h)

set(gca, ‘Line Width’,2,‘Font Size’,16)

xlabel(‘x’,‘Fontsize’,16)

ylabel(‘y’,‘Fontsize’,16)

Figure 8.9

Contour plot of the function given in Equation (8.9)

−3 −2.5 −2 −1.5 −1 −0.5 0

−2

−1

saddle point

minimum

504

Nonlinear model regression and optimization

The resulting plot is shown in Figure 8.10. The second critical point is a minimum. A labeled contour plot

that shows the behavior of the function at the saddle point is shown in Figure 8.11. Study the shape of the

function near the saddle point. Can you explain how this type of critical point got the name “saddle”?

Taking the first partial derivatives of the function with respect to x and y, we obtain the following analytical

expression for the gradient:

rfx; yðÞ¼

ð1 þ xÞe

xþy

þ 2y



We begin with an initial guess value of x

ð0Þ

¼ð1; 0Þ:

Figure 8.10

Contour plot of the function given by Equation (8.9) showing the function values at different contour levels near the

minimum point

−0.24312

−0.076913

−

0.076913

−0.076913

0.089295

0.2555

0.42171

0.58792

.792

0.58792

0.75413

0 92034

0.92034

1.0865

1.2528

1.252 8

1.41

−3 −2.5 −2 −1.5 −1 −0.5 0

−1

−0.5

0.5

1.5

Figure 8.11

The behavior of the function at the saddle point

0.24508

0.42266

0.60024

0.77782

0.9554

1.133

1.3106

1.4881

1.6657

1.8433

2.0209

2.1984

2.198

2.376

2.5536

2.7312

−1.5 −1 −0.5

1.5

2.5

3.5

Use the command surf(x, y, z) in MATLAB to reveal the shape of this function in two variables.

This might help you to answer the question.

505

8.3 Unconstrained multivariable optimization

rf 1; 0ðÞ¼

1=e



Next we minimize the function:

f x

0ðÞ

 αrf x

0ðÞ



¼ f 1  0  α; 0 



¼e

 1þ

ðÞ



The function to be minimized is reduced to a single-variable function. Any one-dimensional minimization

method, such as successive parabolic interpolation, golden section search, or Newton’s method can be

used to obtain the value of α that minimizes the above expression.

We use successive parabolic interpolation to perform the single-variable minimization. For this purpose,

we create a MATLAB function program that calculates the value of the function f αðÞat any value of α.To

allow the same function m-file to be used for subsequent iterations, we generalize it by passing the values

of the current guess point and the gradient vector to the function.

MATLAB program 8.8

function f = xyfunctionalpha(alpha, x, df)

% Calculates the function f(x-alpha*df)

% Input variables

% alpha : scalar value of the step size

% x : vector that speciﬁes the current guess point

% df : gradient vector of the function at x

f = (x(1)-df(1)*alpha)*exp(x(1)-df(1)*alpha + x(2)-df(2)*alpha) + ...

(x(2) - df(2)*alpha)^2;

Program 8.3, which lists the function m-file that performs a one-dimensional minimization using the

parabolic interpolation method, is slightly modified so that it can be used to perform our line search. In this

user-defined function, the guessed point and the gradient vector are added as input parameters and the

function is renamed as steepestparabolicinterpolation (see Program 8.10). We type the

following in the Command Window:

steepestparabolicinterpolation(‘xyfunctionalpha’, [0 10],0.01,

[−1, 0], [0, −exp(−1)])

The output is

x0 = 0.630535 x2 = 0.630535 f(x0) = −0.410116 f(x2) = −0.410116

x_min = 0.630535 f(x_min) = −0.410116

number of iterations = 13

The optimum value of α is found to be 0.631, at which the function value is −0.410. The new point x

ð1Þ

(−1, 0.232). The gradient at this point is calculated as

rf 1; 0:232ðÞ¼

6  10

5



The gradient is very close to zero. We conclude that we have reached the minimum point in a single

iteration. Note that the excellent initial guessed point and the behavior of the gradient at the initial guess

contributed to the rapid convergence of the algorithm.

506

Nonlinear model regression and optimization