King M.R., Mody N.A. Numerical and Statistical Methods for Bioengineering: Applications in MATLAB

Подождите немного. Документ загружается.

We can automate the steepest descent algorithm by creating an m-file that iteratively calculates

the gradient of the function and then passes this value along with the guess point to

steepestparabolicinterpolation. Program 8.9 is a function that minimizes the

multivariable function using the line search method of steepest descent. It calls Program 8.10 to

perform one-dimensional minimization of the function along the search direction by optimizing α.

MATLAB program 8.9

function steepestdescent(func, funcfalpha, x0, toldf)

% Performs unconstrained multivariable optimization using the steepest

% descent method

% Input variables

% func: calculates the gradient vector at x

% funcfalpha: calculates the value of f(x-alpha*df)

% x0: initial guess point

% toldf: tolerance for error in gradient

% Other variables

maxloops = 20;

ab = [0 10]; % smallest and largest values of alpha

tolalpha = 0.001; % tolerance for error in alpha

df = feval(func, x0);

% Miminization algorithm

for i = 1:maxloops

alpha = steepestparabolicinterpolation(funcfalpha, ab, ...

tolalpha, x0, df);

x1 = x0 - alpha*df;

x0 = x1;

df = feval(func, x0);

fprintf(‘at step %2d, norm of gradient is %5.4f \n’,i, norm(df))

if norm(df) < toldf

break

end

fprintf(‘number of steepest descent iterations is %2d \n’,i)

fprintf(‘minimum point is %5.4f, %5.4f \n’,x1)

MATLAB program 8.10

function alpha = steepestparabolicinterpolation(func, ab, tolx, x, df)

% Successive parabolic interpolation is used to ﬁnd the minimum

% of a unimodal function.

% Input variables

% func: nonlinear function to be minimized

% ab : initial bracketing interval [a, b]

% tolx: tolerance in estimating the minimum

% x : guess point

% df : gradient vector evaluated at x

507

8.3 Unconstrained multivariable optimization

% Other variables

k = 0; % counter

maxloops = 20;

% Set of three points to construct the parabola

x0 = ab(1);

x2 = ab(2);

x1 = (x0 + x2)/2;

% Function values at the three points

fx0 = feval(func, x0, x, df);

fx1 = feval(func, x1, x, df);

fx2 = feval(func, x2, x, df);

% Iterative solution

while (x2 - x0) > tolx

% Calculate minimum point of parabola

numerator = (x2^2 - x1^2)*fx0 - (x2^2 - x0^2)*fx1 + (x1^2 - x0^2)*fx2;

denominator = 2*((x2 - x1)*fx0 - (x2 - x0)*fx1 + (x1 - x0)*fx2);

xmin = numerator/denominator;

% Function value at xmin

fxmin = feval(func, xmin, x, df);

% Select set of three points to construct new parabola

if xmin < x1

if fxmin < fx1

x2 = x1;

fx2 = fx1;

x1 = xmin;

fx1 = fxmin;

else

x0 = xmin;

fx0 = fxmin;

end

else

if fxmin < fx1

x0 = x1;

fx0 = fx1;

x1 = xmin;

fx1 = fxmin;

else

x2 = xmin;

fx2 = fxmin;

end

k=k+1;

if k > maxloops

break

end

alpha = xmin;

fprintf(‘x0 = %7.6f x2 = %7.6f f(x0) = %7.6f f(x2)= %7.6f \n’, x0, x2, fx0, fx2)

508

Nonlinear model regression and optimization

fprintf(‘x_min = %7.6f f(x_min) = %7.6f \n’,xmin, fxmin)

fprintf(‘number of parabolic interpolation iterations = %2d \n’,k)

Using an initial guessed point of (−1, 0) and a tolerance of 0.001, we obtain the following solution:

steepestdescent(‘xyfunctiongrad’,‘xyfunctionalpha’ ,[−1, 0],

0.001)

x0 = 0.630535 x2 = 0.630535 f(x0) = −0.410116 f(x2) = −0.410116

x_min = 0.630535 f(x_min) = −0.410116

number of parabolic interpolation iterations = 13

at step 1, norm of gradient is 0.0000

number of steepest descent iterations is 1

minimum point is −1.0000, 0.2320

Instead if we start from the guess point (0, 0), we obtain the output

x0 = 0.000000 x2 = 1.000812 f(x0) = 0.000000 f(x2) = −0.367879

x_min = 1.000520 f(x_min) = −0.367879

number of parabolic interpolation iterations = 21

at step 1, norm of gradient is 0.3679

x0 = 0.630535 x2 = 0.630535 f(x0) = −0.410116 f(x2) = −0.410116

x_min = 0.630535 f(x_min) = −0.410116

number of parabolic interpolation iterations = 13

at step 2, norm of gradient is 0.0002

number of steepest descent iterations is 2

minimum point is -1.0004, 0.2320

8.3.2 Multidimensional Newton’s method

Newton’s method approximates the multivariate function with a second-order

approximation. Expanding the function about a point x

using a multidimensional

Taylor seri es, we have

f xðÞf x

ðÞþr

f x

ðÞx  x

ðÞþ

x  x

ðÞ

ðÞx  x

ðÞ;

where r

f x

ðÞis the transpose of the gradient vector. The quadratic approximation

is differentiated with respect to x and equated to zero. Thi s yields the following

approximation formula for the minimum:

ðÞΔx ¼rf x

ðÞ; (8:10)

where Δx ¼ x  x

. This method requires the calcul ation of the ﬁrst and second

partial derivatives of the function. Note the similarity between Equations (8.10) and

(5.37). The iterative technique to ﬁnd the solution x that minimizes fðxÞ has much in

common with that described in Section 5.7 for solving a system of nonlinear

equations using Newton’s method. Equation (8.10) reduces to a set of linear equa-

tions in Δx. Any of the methods described in Chapter 2 to solve a system of linear

equations can be used to solve Equation (8.10).

Equation (8.10) exactly calculates the minimum x of a quadratic function. An

iterative process is required to minimize general nonlinear functions. If the Hessian

matrix is invertible then we can rearrange the terms in Equation (8.10) to obtain the

iterative formula

ðkþ1Þ

¼ x

ðkÞ

 Hx

ðkÞ

hi

1

rf x

ðkÞ



: (8:11)

509

8.3 Unconstrained multivariable optimization

In Equation (8.11),  Hx

ðÞ½

1

rfx

ðÞprovides the search (descent) direction. This is

the Newton formula for multivariable minimization. Because the formula is inexact

for a non-quadratic function, we can optimize the step length by adding an addi-

tional parameter α. Equat ion (8.11) becomes

ðkþ1Þ

¼ x

ðkÞ

 α

ðkÞ

hi

1

rfx

ðkÞ



: (8:12)

In Equation (8.12), the search direction is given by Hx

ðkÞ



1

rf x

ðkÞ



and the step

length is modiﬁed by α

Algorithm for Newton’s multidimensional minimization ( α =1)

(1) Provide an initial estimate x

ðkÞ

of the minimum of the objective function fðxÞ. At the

ﬁrst iteration, k =0.

(2) Determine the analytical or numerical form of the ﬁrst and second partial derivatives

of fðxÞ.

(3) Evaluate rfxðÞand HxðÞat Δx

ðkÞ

(4) Solve the system of linear equations Hx

ðkÞ



Δx

ðkÞ

¼rf x

ðkÞ



for Δx

kðÞ

(5) Calculate the next approximation of the minimum x

kþ1

ðÞ

¼ x

ðÞ

þ Δx

ðÞ

(6) Repeat steps (3)–(5) until the method has converged upon a solution.

Algorithm for modiﬁed Newton’s multidimensional minim ization (α ≠ 1)

(1) Provide an initial estimate x

ðkÞ

of the minimum of the objective function fðxÞ.

(2) Determine the analytical or numerical form of the ﬁrst and second partial derivatives

of fðxÞ.

(3) Calculate the search direction s

ðkÞ

¼Hx

ðkÞ



1

rf x

ðkÞ



(4) Perform single-parameter optimization to determine the value of α

that minimizes

f x

ðkÞ

þ α

ðkÞ



(5) Calculate the next approximation of the minimum x

kþ1ðÞ

¼ x

ðkÞ

þ α

ðkÞ

(6) Repeat steps (3)–(5) until the method has converged upon a solution.

When the method has converged upon a solution, it is necessary to check if the

point is a local minimum. This can be done either by determining if H evaluated at

the solution is positive deﬁnite or by perturbing the solution slightly along multiple

directions and observing if iterative optimization recovers the solution each time. If

the point is a saddle point, perturbation of the solution and subsequent optimization

steps are likely to lead to a solution corresponding to some other critical point.

Newton’s method has a quadratic convergence rate and thus minimizes a function

faster than other methods, when the initial guessed point is close to the minimum.

Some difﬁcul ties encountered with using Newton’s method are as follows.

(1) A good initial approximation close to the minimum point is required for the method

to demonstrate convergence.

(2) The ﬁrst and second partial derivatives of the objective function should exist. If the

expressions are too complicated for evaluation, ﬁnite difference approximations

may be used in their place.

(3) This method may converge to a saddle point. To ensure that the method is not

moving towards a saddle point, it should be veriﬁed that Hx

ðkÞ



is positive deﬁnite

at each step. If the Hessian matrix evaluated at the current point is not positive

deﬁnite, the minimum of the function will not be reached. Techniques are available

510

Nonlinear model regression and optimization

to force the Hessian matrix to remain positive deﬁnite so that the search direction

will lead to improvement (reduction) in the function value at each step.

The advantages and drawbacks of the method of steepest descent and Newton’s

method are complementary. An efﬁcient and popular minimization algorithm is the

Levenberg–Marquart method, which combines the two techniques in such a way

that minimization begins with steepest descent. When the minimum point is near

(e.g. Hessian is positive deﬁnite), convergence slow s down , and the iterative routi ne

switches to Newton’s method, producing a more rapid convergence.

Using MATLAB

Optimization Toolbox contains the built-in function fminunc that searches for the

local minimum of a multivariable objective function. This function operates on two

scales. It has a large-scale algorithm that is suited for an unconstrained optimization

problem consisting of many variables. The medium-scale algorithm should be chosen

when optimizing a few variables. The latter algorithm is a line search method that

calculates the gradient to provide a search direction. It uses the quasi-Newton method

to approximate and update the Hessian matrix, whose inverse is used along with the

gradient to obtain the search direction. In the quasi-Newton method, the behavior of

the function fðxÞand its gradient rfðxÞ is used to determine the form of the Hessian at

x. Newton’s method, on the other hand, calculates H directly from the second partial

derivatives. Gradient methods, and therefore the fminunc function, should be used

when the function derivative is continuous, since they are more efﬁcient.

The default algorithm is large-scale. The large-scale algorithm approximates the

objective function with a simpler function and then establishes a trust region within

which the function minimum is sought. The second partial derivatives of the objec-

tive function can be made available to fminunc by calculating them along with the

objective function in the user-deﬁned functi on ﬁle. If the options structure

instructs fminunc to use the user-supplied Hessian matrix, these are used in place

of the numerical approximations generated by the algorithm to approximate the

Hessian. Only the large-scale algorithm can use the user-supplied Hessian matrix

calculations, if provided. Note that calculating the gradient rfðxÞ along with the

function fðxÞ is optional when using the medium-scale algorithm but is required

when using the large-scale algorithm.

One form of the syntax is

x = fminunc(func, x0, options)

is the initial guess value and can be a scalar, vector, or matrix. Use of optimset

to construct an options structure was illustrated in Section 8.2.3. Options can be

used to set the tolerance of x, to set the tolerance of the function value, to specify use

of user-supplied gradient calculations, to specify use of user-supplied Hessian cal-

culations, whether to proceed with the large-scale or medium-scale algorithm by

turning “LargeScale” on or off, and various other speciﬁcs of the algorithm. To

tell the function fminunc that func also returns the gradient and the Hessian

matrix along with the scalar function value, create the following structure:

options = optimset(‘GradObj’, ‘ on’, ‘Hessian’, ‘on’)

to be passed to fminunc.Whenfunc supplies the ﬁrst partial derivatives and the

second partial derivatives at x along with the function value, it should have three

511

8.3 Unconstrained multivariable optimization

output arguments in the following order: the scalar-valued function, the gradient

vector, followed by the Hessian matr ix (see Example 8.2). See help fminunc for

more details.

Example 8.2

Minimize the function given in Equation (8.9) using multidimensional Newton’s method.

The analytical expression for the gradient was obtained in Example 8.1 as

rfx; yðÞ¼

ð1 þ xÞe

xþy

þ 2y



The Hessian of the function is given by

Hx; yðÞ¼

2 þ xðÞe

xþy

1 þ xðÞe

xþy

1 þ xðÞe

xþy

þ 2



MATLAB Program 8.11 performs multidimensional Newton’s optimization, and Program 8.12 is a function

that calculates the gradient and Hessian at the guessed point.

MATLAB program 8.11

function newtonsmulti Doptimization(func, x0, toldf)

% Newton’s method is used to minimize a multivariable objective function.

% Input variables

% func : calculates gradient and Hessian of nonlinear function

% x0 : initial guessed value

% toldf : tolerance for error in norm of gradient

% Other variables

maxloops = 20;

[df, H] = feval(func,x0);

% Minimization scheme

for i = 1:maxloops

deltax = - H\df; % df must be a column vector

x1 = x0 + deltax;

[df, H] = feval(func,x1);

if norm(df) < toldf

break % Jump out of the for loop

end

x0 = x1;

end

fprintf(‘number of multi-D Newton’’s iterations is %2d \n’,i)

fprintf(‘norm of gradient at minimum point is %5.4f \n’, norm(df))

fprintf(‘minimum point is %5.4f, %5.4f \n’,x1)

MATLAB program 8.12

function [df, H] = xyfunctiongradH(x)

% Calculates the gradient and Hessian of f(x)= x*exp (x + y) + y^2

df = [(1 + x(1))*exp(x(1) + x(2)); x(1)*exp(x(1) + x(2)) + 2*x(2)];

512

Nonlinear model regression and optimization

H = [(2 + x(1))*exp(x(1) + x(2)), (1 + x(1))*exp(x(1) + x(2)); ...

(1 + x(1))*exp(x(1) + x(2)), x(1)*exp(x(1) + x(2)) + 2];

We choose an initial point at (0, 0), and solve the optimization problem using our optimization function

developed in MATLAB:

newtonsmultiDoptimization(‘xyfunctiongradH’, [0; 0], 0.001)

number of multi-D Newton’s iterations is 4

norm of gradient at minimum point is 0.0001

minimum point is -0.9999, 0.2320

We can also solve this optimization problem using the fminunc function. We create a function that

calculates the value of the function, gradient, and Hessian at any point x.

MATLAB program 8.13

function [f, df, H] = xyfunctionfgradH(x)

% Calculates the valve, gradient, and Hessian of

% f(x) = x*exp(x + y) + y^2

f = x(1)*exp(x(1) + x(2)) + x(2)^2;

df = [(1 + x(1))*exp(x(1) + x(2)); x(1)*exp(x(1)+ x(2)) + 2*x(2)];

H = [(2 + x(1))*exp(x(1) + x(2)), (1 + x(1))*exp(x(1)+ x(2)); ...

(1 + x(1))*exp(x(1) + x(2)), x(1)*exp(x(1) + x(2)) + 2];

Then

options = optimset(‘GradObj’,‘on’,‘Hessian’,‘on’);

fminunc(‘xyfunctionfgradH’,[0; 0], options)

gives us the output

Local minimum found.

Optimization completed because the size of the gradient is less than

the default value of the function tolerance.

ans =

−1.0000

0.2320

8.3.3 Simplex method

The simplex method is a direct method of minimization since only function evalua-

tions are required to proceed iteratively towards the minimum point. The method

creates a geometric shape called a simplex. The simplex has n + 1 vertices, where n is

the number of variables to be optimized. At each iteration, one point of the simplex is

discarded and a new point is added such that the simplex gradually moves in the

variable space towards the minimum. The original simplex algorithm was devised by

Spendley, Hext, and Himsworth, according to which the simplex was a regular

geometric structure (with all sides of equal lengths). Nelder and Mead developed a

more efﬁcient simplex algorithm in which the location of the new vertex, and the

location of the other vertices, may be adjusted at each iteration, permitting the

simplex shape to expand or contract in the variable space. The Nelder–Mead simplex

structure is not necessarily regular after each iteration. For a two-dimensional

optimization problem, the simplex has the shape of a triangle. The simplex takes

the shape of a tetrahedron or a pyramid for a three-parameter optimization problem.

513

8.3 Unconstrained multivariable optimization

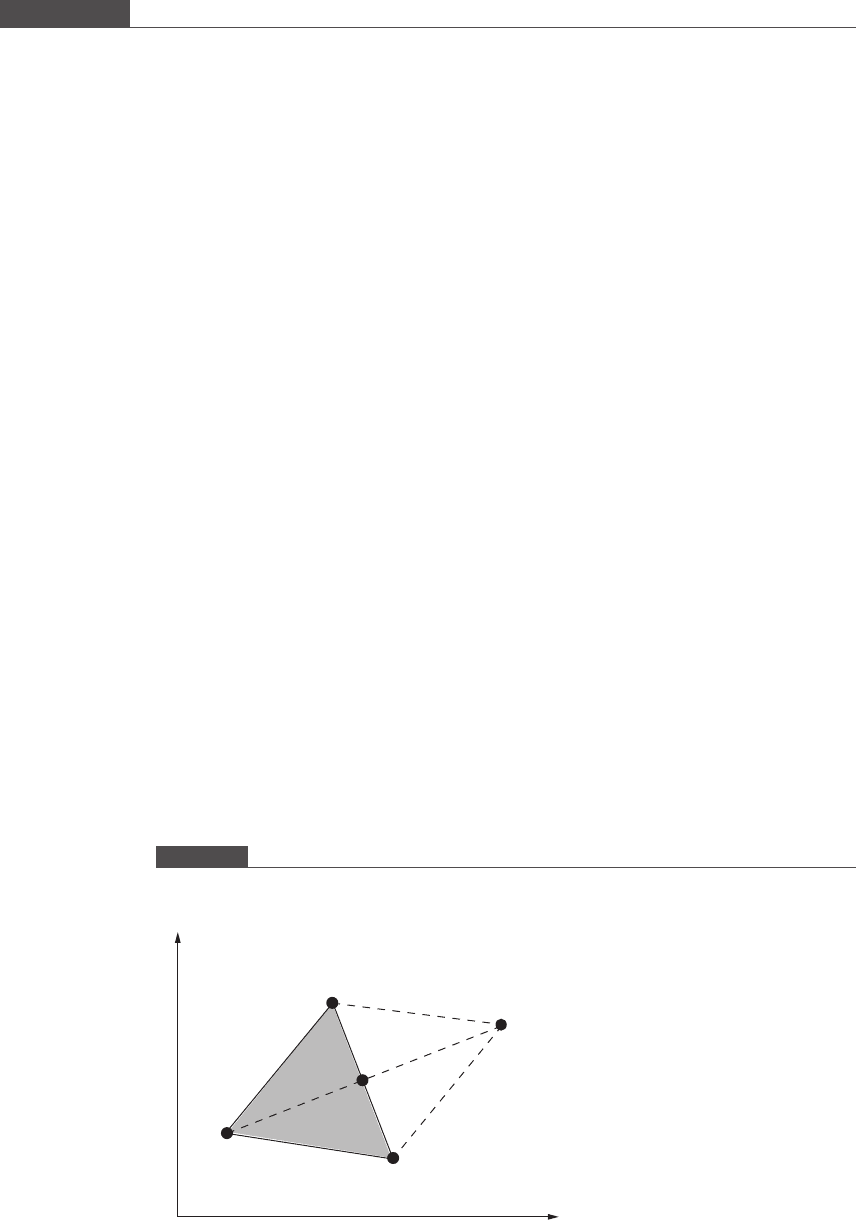
We illustrate the simplex algorithm for the two-dimensional optimization problem.

Three points in the variable space are chosen such that the lines connecting the points

are equal in length, to generate an equilateral triangle. We label the three vertices

according to the function value at each vertex. The vertex with the smallest function

value is labeled G (for good); the vertex with an intermediate function value is labeled

A (for average); and the vertex with the largest function value is labeled B (for bad).

The goal of the simplex method, when performing a minimization, is to move

downhill, or away, from the region where the function values are large and towards

the region where the function values are smaller. The function values decrease in the

direction from B to G and from B to A. Therefore, it is likely that even smaller values

of the functi on will be encountered if one proceeds in this direction. To advance in

this direction, we locate the mirror image of point B across the line GA . To do this

the midpoint M on the line GA is located. A line is drawn that connects M with B,

which has a width w. This line is extended past M to a point S such that the width of

the line BS is 2w. See Figure 8.12.

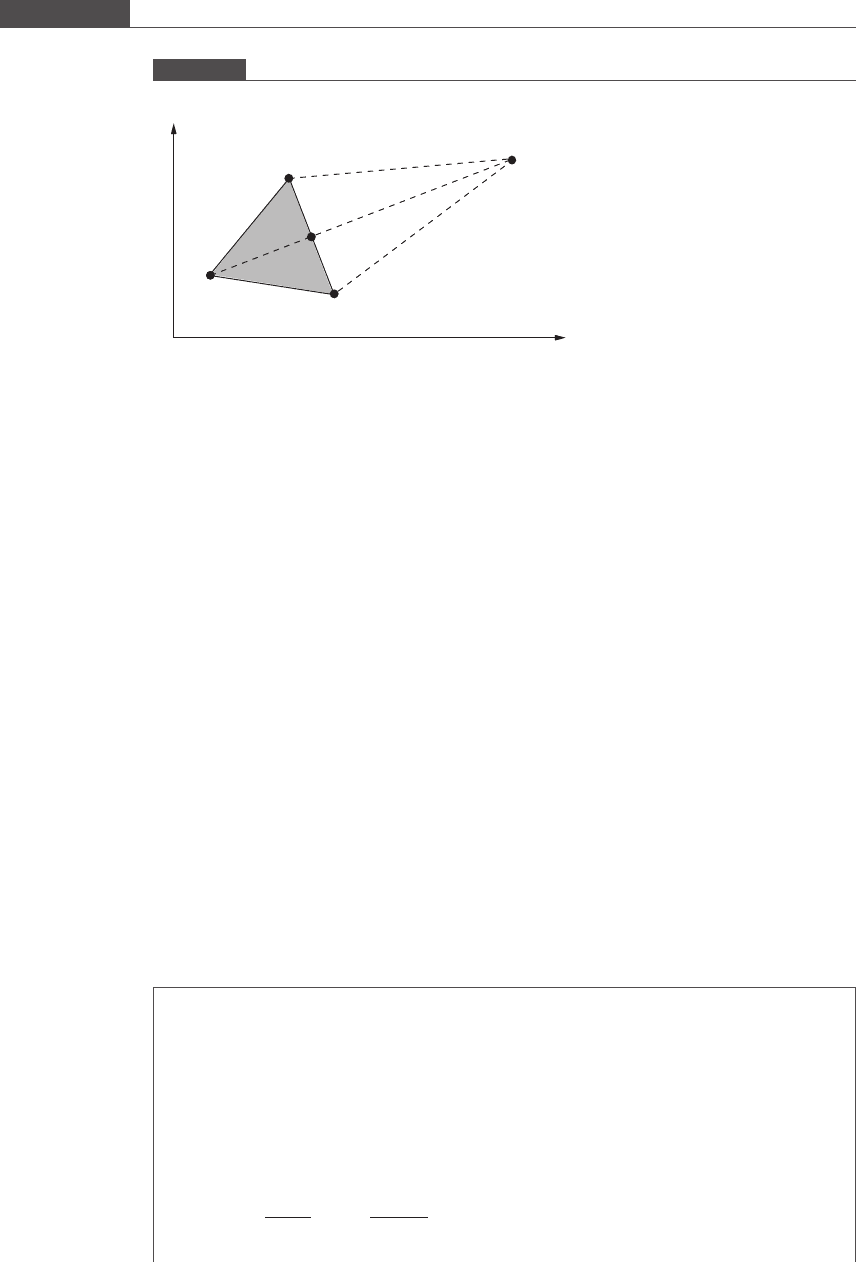
The function value at S is computed. If f SðÞ

fðGÞ, then the point S is a signiﬁcant

improvement over the point B. It may be possible that the minimum lies further

beyond S. The line BS is extended further to T such that the width of MT is 2w and

BT is 3w (see Figure 8.13). If f TðÞ

fðSÞ, then further improvement has been made in

the selection of the new vertex, and T is the new vertex that replaces B.Iff TðÞ

fð

SÞ,

then point S is

retained and T is discarded.

On the other hand, if f SðÞfðBÞ, then no improvement has resulted from the

reﬂection of B across M. The poin t S is discarded and another point C, located at a

distance of w/2 from M along the line BS, is selected and tested. If f CðÞfðBÞ, then

point C is discarded. Now the original simplex shape must be modiﬁed in order to

make progress. The lengths of lines GB and GA contrac t as the points B and A are

retracted towards G. After shrinking the triangle, the algorithm is retried to ﬁnd a

new vertex.

A new simplex is generated at each step such that there is an improvement

(decrease) in the value of the function at one vertex point. When the minimum is

approached, in order to ﬁne-tune the estimate of its location, the size of the simplex

(triangle in two-dimensional space) must be reduced.

Figure 8.12

Construction of a new triangle GSA (simplex). The original triangle is shaded in gray. The line BM is extended beyond M

by a distance equal to w

514

Nonlinear model regression and optimization

Because the simplex method only performs function evaluations, it does not make

any assumptions regarding the smoothness of the function and its differentiability

with respect to each variable. Therefore, this method is preferred for use with

discontinuous or non-smooth functions. Moreover, since partial derivative calcu-

lations are not required at any step, direct methods are relatively easy to use.

Using MATLAB

MATLAB’s built-in function fminsearch uses the Nelder–Mead implementation

of the simplex method to search for the unconstrained minimum of a function. This

function is well suited for optimizing multivariable problems whose objective func-

tion is not smooth or is discontinuous. This is because the fminsearch routine only

evaluates the objective function and does not calculate the gradient of the function.

The syntax is

x = fminsearch(func, x0)

[x, f] = fminsearch(func, x0, options)

The algorithm uses the initial guessed value x

to construct n additional points,

and 5% of ea ch element of x

is added to x

to derive the n + 1 vertices of the

simplex. Note that func is the handle to the function that calculates the scalar value

of the objective function at x. The function output is the value of x that minimizes

func, and, optionally, the value of func at x.

Figure 8.13

Nelder–Mead’s algorithm to search for a new vertex. The point T may be an improvement over S

Box 8.3 Nonlinear regression of pixel intensity data

We wish to study the morphology of the cell synapse in a cultured aggregate of cells using immuno-

fluorescence microscopy. Cells are fixed and labeled with a fluorescent antibody against a protein

known to localize at the boundary of cells. When the pixel intensities along a line crossing the cell

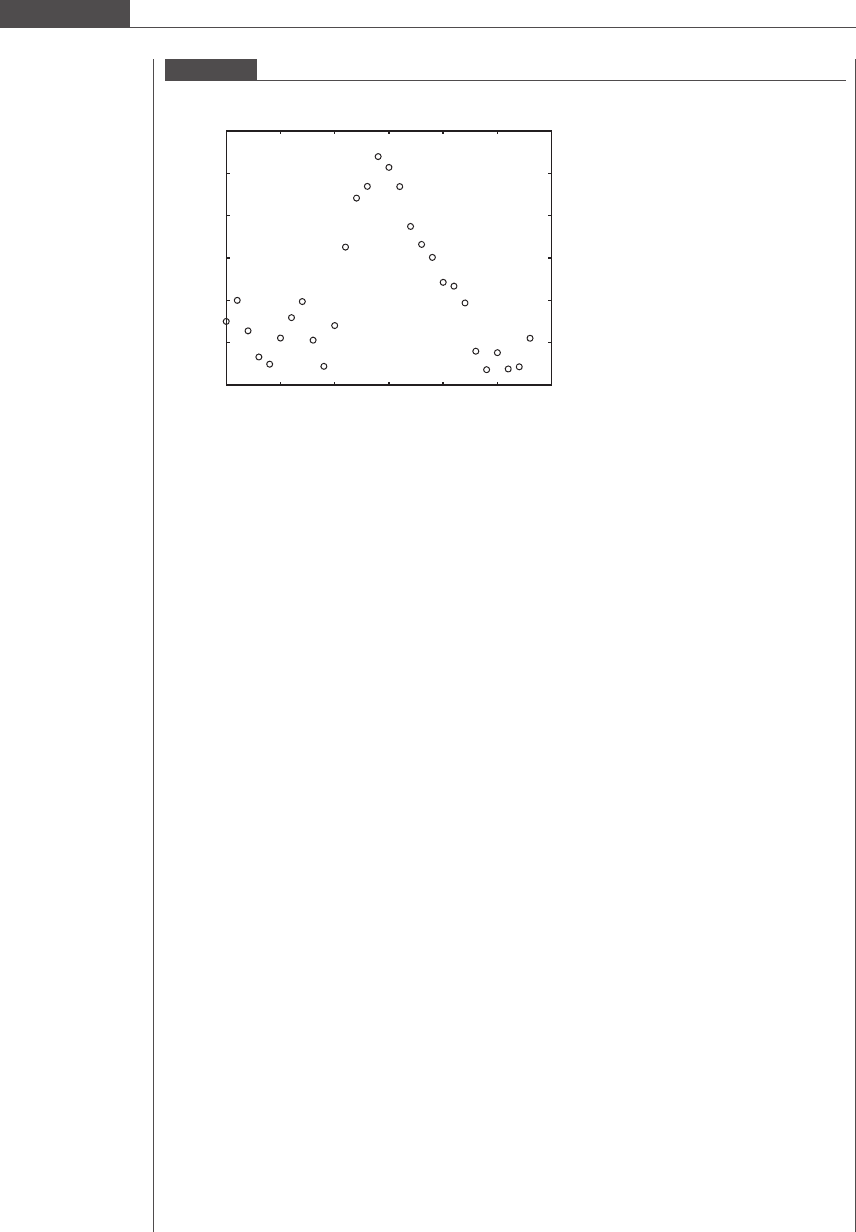
synapse are measured, the data in Figure 8.14 are produced.

We see a peak in the intensity near x = 15. The intensity attenuates to some baseline value (I ~

110) in either direction. It was decided to fit these data to a Gaussian function of the following form:

fðxÞ¼

ﬃﬃﬃﬃﬃﬃﬃﬃ

2πσ

exp 

x  μðÞ

2σ

þ a

;

515

8.3 Unconstrained multivariable optimization

where a

is an arbitrary scaling factor, a

represents the baseline intensity, and the other two

model parameters are σ and μ of the Gaussian distribution. In this analysis, the most important

parameter is σ, as this is a measure of the width of the cell synapse and can potentially be used to

detect the cell membranes separating and widening in response to exogenous stimulation. The

following MATLAB program 8.14 and user-defined function were written to perform a nonlinear least

squares regression of this model to the acquired image data using the built-in fminsearch

function.

MATLAB program 8.14

% This program uses fminsearch to minimize the error of nonlinear

% least-squares regression of the unimodal Gaussian model to the pixel

% intensities data at a cell synapse

% To execute this program place the data ﬁles into the same directory in

% which this m-ﬁle is located.

% Variables

global data % matrix containing pixel intensity data

Nﬁles = 4; % number of data ﬁles to be analyzed, maximum allowed is 999

for i = 1:Nﬁles

num = num2str(i);

if length(num) == 1

ﬁlename = [ ‘ data00’,num,’.dat’];

elseif length(num) == 2

ﬁlename = [ ‘ data0’,num,’.dat’];

else

ﬁlename = [ ‘ data’,num,’.dat’];

end

data = load(ﬁlename);

p = fminsearch(‘PixelSSE’,[15,5,150,110]);

Figure 8.14

Pixel intensities exhibited by a cell synapse, where x specifies the pixel number along the cell synapse

0 5 10 15 20 25 30

100

110

120

130

140

150

160

Intensity

516

Nonlinear model regression and optimization