Киреев П.С. Физика полупроводников

Подождите немного. Документ загружается.

щих компонентов тензоров ν-эллипсоида, записав их в одной

•

той

же системе координат. Если провести соответствующие рас-

четы, то получим:

для проводимости

= σ

= βημ

;

η = Μη

;

(τ)

m* 3 \mt mi

для проводимбсти Холла

е*п

(τ

)

Gijk

— = ~У—+

*2 з I .

)

rtlt tnit7l

(50.14)

(50.15)

Gijkl '

(τ

) _ .. Jm^

-5" Fijki·

(т)

\mj

(50.16)

Значения коэффициентов F

приведены в табл. 15 для \вух

случаев: экстремумы находятся вдоль направлений [100], ^к в $эем-

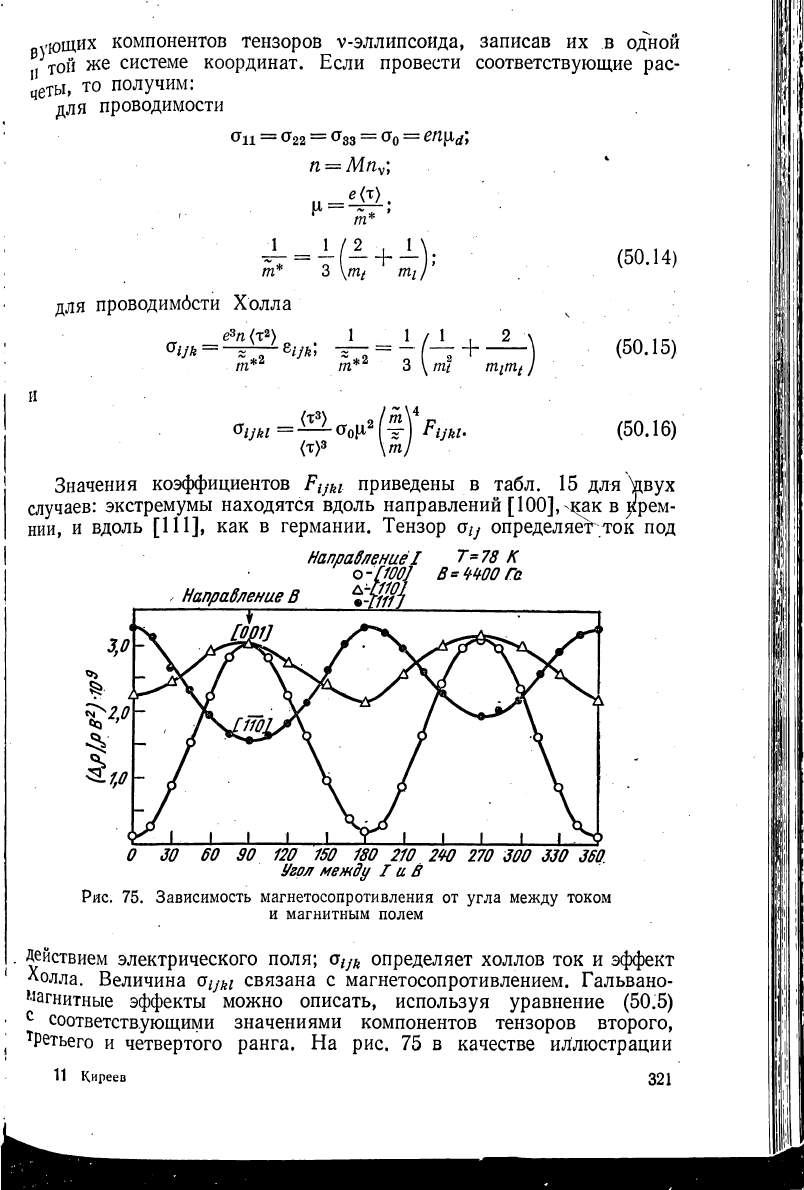
нии, и вдоль [111], как в германии. Тензор σ/у определяет ток под

Напрадлениё I Τ =78 К

о-Г 100] В*

WOO

Га

Направление

В *-τίίΐ7

О 30 60 30 120 150 180 210 240 270 300 330 360.

Угол между Τ и В

Ряс. 75. Зависимость магнетосопротивления от угла между током

и магнитным полем

Действием электрического поля; a

iJk

определяет холлов ток и эффект

Холла. Величина o

iJk

i связана с магнетосопротивлением. Гальвано-

магнитные эффекты можно описать, используя уравнение (50.5)

соответствующими значениями компонентов тензоров второго,

Ретьего и четвертого ранга. На рис. 75 в качестве иллюстрации

11 Киреев

321

ga(p^)

от

гла

между током j и магнитным полем В для гер^

приведена зависимость коэффициента магнетосопротивления //

J №

Ро

ния м-типа.

§ 51. ТЕНЗОРЕЗИСТИВНЫЙ ЭФФЕКТ. ТЕНЗОЧУВСТВИТЕЛЬНОСТЬ

Тензорезистивным эффектом, или тензосопротивлением \

вают изменение электрического сопротивления полупроводника в р

зультате действия нагрузки, создающей деформацию. Непосредственно

тензосопротивление не вытекает из кинетического уравнения, однако

его необходимо отнести к кинетическим явлениям, поскольку оно

представляет собой изменение одного из важнейших кинетических

явлений —сопротивления, или проводимости,— под действием, напря-

жений в теле, создаваемых внешней'нагрузкой.

Для описания тензорезистивного эффекта необходимы некоторые

понятия из теории упругости, которые кратко напомним. Деформа-

ция тела приводит к тому, что координаты точек тела меняются.

Если до деформации координаты точек тела определяются радиу-

сом-вектором г, а в деформированном теле г', то

« = г'-г

(51.1)

называется вектором деформации, или вектором смещения. Задание

вектора и как функции точек кристалла

—

и (г)

—

полностью опреде-

ляет состояние деформированного тела. Деформация тела может быть

рписана симметричным тензором деформации u

• ' = Ш +

(51Я

Тензор деформации, записанный в своих главных осях, имеет

диагональный вид-

Uik = vLm

. (51.3)

Тензор деформации u

определяет изменение расстояний между

точками тела при деформации.

Если в недеформированном теле расстояние между двумя точка-

ми dl, а в деформированном теле расстояние между теми же точка·

ми равно dl\ то связь между dl' и dl можно выразить через тензор

деформации \x

. Действительно,

= dx

+ dy

+ dz* = 2 dx! (

3.3, 3 .

= Σ

ά/2==

Σ (

i +

= Σ i

* +

ZdXidUi

+ duf). (

i=l i=\

Тензосопротивление в некоторых случаях называют пьезосопроти

вле^

322

Пренебрегая величиной du\ как величиной второго порядка

малости, выражая du

{

через dx

dXk (51

.• k=\

учитывая (51.4), получим

Г = = ^ +

2 ^ d

XidXk

dl>

+ 2 + Ц-) =

t=l ' k==\ i,k

= dl

+ 2^u

. (51.7)

i, k

Если тензор деформации имеет диагональный вид (51.3), то (51.7)

упрощается:

dl'

-dl

= 2% u

dxidx

= 2 2'u^dxl (51.8)

Из (51.8) можем записать

άΐ = -\idl

+ 2^n

dxidx

= dl лГl+2£u

1к

щп

. (51.9)

' i,k У i, k

Относительное удлинение вдоль направления η = (п

, п

) можно

выразить через тензор деформации следующим образом:

= V

Σ ~

= Σ ^ηιηί. (51.10)

- * ι, k

Найдем изменение объема при деформации:

dx' = d^dy'dz' = dx(

+ u

>) dy (1 + u

>) dz (1 +u<

>) =

— dx(l +u

(1)

+ u

(2)

+ u

(3)

), (51.11)

или '

dx'— dx

du>i

Таким образом, главные значения тензора деформации определяют

относительные удлинения вдоль главных осей тензора, а их сумма —

относительное изменение объема.

Тензор деформации {u

} можно представить в несколько другом

ВИ

ДЕ, для этого запишем тождество:

+^Y2

U|,

)

'*·

(51ЛЗ)

Второй тензор, имеющий диагональный вид с одинаковыми диаго-

нальными элементами, равными одной трети относительного измене-

11Ия

объема Δ, называют тензором всестороннего сжатия.

323

Тензор, определенный членом, стоящим в квадратной скобк

(51.13), называют тензором сдвига. Так как для него сумма диаг<^ '

нальных элементов равна нулю, то при чистом сдвиге изменена '«

объема не происходит. ' .

При деформации тела в нем возникают внутренние напряжения «

стремящиеся вернуть тело в равновесное, недеформированное состоя! '

ние. Они могут быть описаны некоторым симметричным тензоров

второго ранга

—

тензором напряжений {р

\. Величина р^ представ,

ляет собой проекцию силы на ось i, действующую на единичную пло-

щадку, перпендикулярную оси k. Сила F

, действующая на единичный

объем тела, может быть выражена через тензор напряжений ρ сле-

дующи м образом:

(1)

= divp, (51.14)

)· (51.15)

Между тензором деформации и тензором напряжений должна быть

определенная связь. Действительно, с ростом деформации напряже-

ния должны возрастать. В пределах упругих деформаций между

деформацией и напряжением на основании закона Гука должна су-

ществовать линейная зависимость. Величину, связывающую деформа-

цию с напряжением, называют обычно модулем упругости. Поскольку

в общем случае деформация и напряжение являются тензорами вто-

рого ранга, и модуль упругости должен быть тензором, причем

более высокого ранга, именно четвертого. Обозначим его элементы

через Ким, тензор λ называют тензором модулей упругости, или

просто тензором упругости. В соответствии с законом Гука запишем

\ . Р** = 2>

Шт

/т

(51.16)

Тензор модулей упругости λ симметричен по парам своих индек-

сов:

hijki = hj

i = Xiji

==K

·• . (51.17)

так как он связывает между собой два симметричных тензора ρ

и u

. С учетом (51.17) в общем случае из 81 элемента тензора λ

отличными друг от друга элементами могут быть не более 21. С уче*

том свойств симметрии решетки число независимых модулей упрУ*

гости может быть уменьшенное. Например, в триклинной системе

число независимых модулей равно 18, в ромбоэдрической

—

12, в гек-

сагональной

—

5 и в кубической только три, которые можно обозна-

чить как

λχχχχ] h

yy'

'к

χ уху. у (51.

Изотропные тела характеризуются всего двумя модулями упрУ"

гости

—

модулями сдвига и всестороннего сжатия.

324

Если тело находится в равновесии, то полная сила, действующая

а единичный объем тела, равна нулю, следовательно, условием рав-

новесия является

k -

Пусть ρ есть внешнее давление, действующее на тело. Возьмем

элемент поверхности dS. Внешняя сила уравновешивается внутрен-

ними напряжениями:

pdSi^ptdS^^VikdSk. . (51.20)

Обозначим dS = ndS, где η —внешняя нормаль к поверхности

тела. В таком случае

dS = %p

dS, (51.21)

или

Ρι

= Σ (

б1

где n

—

проекция нормали на ось k. При всестороннем сжатии

Р/

= -р и, учитывая, что давление носит нормальный характер,

получим

= -pbik. (51.23)

Если тело подвергнуть одностороннему сжатию ρ

(0, 0, ρ), то

/0 0 0\

{Р^} = (0 0 0 ]. "-N(51.24)

\о о -р) )

В случае, когда давление определяется вдоль направлений η ==

*τ(

ι*

з)> тензор напряжения имеет вид

= — рщп

. (51.25)

Учитывая связь (51.16) между p

и'и

/ш

, можно выразить дефор-

мацию через внешнее давление. Поскольку тензор модулей упру гос-

тей имеет значительно меньше 81 компонента, для него используют

обозначения, указывая не четыре индекса, а только два. Например,

случае кристаллов с кубической решеткой вводят следующие обо-

значения:

^1111

= λ

χχχχ

= С

; λ

112

2 = Ci

;

44·

Компоненты с^ являются симметричными относительно своих

индексов.

Перейдем к описанию тензорезистивного эффекта. Пусть вещество

Ха

рактеризуется тензором удельного сопротивления р° с компонен-

тами ph.

325

Если полупроводник деформирован, то его удельное сопротивл^

ние изменилось, оно равно р

или р^. Величина р

—

р°, или Р^ —ро'

представляет собой изменение удельного сопротивления в результат

действия нагрузки, вызывающей деформацию и напряжения в поли.

проводнике. Изменение удельного сопротивления можно выразить

двояким образом: либо через напряжения, либо через деформацию

Поскольку между напряжением и деформацией существует вполне

определенная связь, оба способа описания являются эквивалентными

Выразим изменение сопротивления р

—р° через тензор напряже^

ния ρ

в виде

- Р

°ik

= Ρ

°ik

штРш>

(51.26)

ИЛИ

р^рц

(51.27)

9lk

Pik

=Zn

Pim. (51.28)

Ρ ik Im

Тензор четвертого ранга п

Шт

называют обычно тензором

коэффи-

циентов пьезосопротивления, или тензором пьезосопротивления.

Для кубического кристалла тензор пьезосопротивления имеет

всего три различные величины, которые для простоты изображаются

величинами с двумя индексами:

Яц11

; Jtll22

12>

12ΐ2

;Πι;

44· (51.29)

Если учесть (51.16), то p]

можно выразить через тензор дефор-

мации и тензор модулей упругости в виде

PLk'=P?J

+S"i«mP/«^=p2

fl+ Σ niklmhmstUst). (51-30)

\ Im / \lm,st )

При экспериментальном исследовании тензорезистивного эффекта

выбирают образец в виде стержня прямоугольного сечения, который

подвергаю т одностороннему сжатию или растяжению. Если ток на-

правлен вдоль оси, по которой направлено растяжение, то мы имеем

продольный эффект, если ток направлен под углом 90° к оси, вдоль

которой приложена внешняя нагрузка, то мы имеем поперечный

эффект.

Запишем выражение для сопротивления р* при одностороннем

сжатии (р>0), учитывая (51.25):

рIk

P°ik(

+ Σ

niklmPlm)

= Pi

(1 - Ρ Σ ЯШпЛяД (

\ Im J \ Im J '

Пусть ток j течет вдоль оси стержня, тогда j

= jn

. Найде*

компоненты поля £,· на основании закона Ома:

i = Σ Piklk = Σ

P°ik(

- ΡΣ

ПШтЩПт)

. (51 ·

32)

k k \ Im J

326

Напряженность поля Ε вдоль оси стержня обозначим через Е":

ЕП

= (Еп) (51.33)

t=l

Назовем продольным удельным сопротивлением р" величину, рав-

ную отношению Е" к /:

„ Σ

μ ' . ^

=— = (ι - Ρ ^ЩмтЪпЛпьЩ. (51.34)

ik \ lm /

При

= 0

= (51.35)

Продольным коэффициентом тензосопротивления, или тензочув-

ствительностью по напряжению, называют величину щ (или ni

ong

pi!

— pll

*'~W=ir· (51.36)

Тензосопротивление вдоль оси образца можно выразить с помощью

коэффициента щ:

рИ

рП(1

-π,ρ). (51.37)

Выразим продольный коэффициент тензосопротивления щ через

тензор пьезосопротивления, исходя из (51.36), (51.35) и (51.34):

Σ ЩытЩЩЩПт. · (51.38)

ikltn

Сумма (51.38) легко вычисляется, если учесть (51.29):

= Яп К +'п1 +

п\)

+ 2 (л

1а

+ π

) (яХ

п\п\

njnj)

= Ли + 2 (π

+ Я

- π

)

(п\п\

+ ηχ + п\п$. (51.39)

Если образец (стержень) вырезан так, что его ось совпадает

с направлением типа [100], то вектор η имеет только одну ненуле-

вую проекцию

= (1, 0, 0), вследствие чего

•

Я[юо]

= п

пу

= п

= π

F.40)

Если образец вырезан вдоль направления типа [110], π/η =

"(yT'W·

)

[

„οι=

πι1+

+π4

\ (51.41)

Аналогично можно получить

= + + * (51.42)

327

Таким образом, коэффициент тензочувствительности щ по

На

пряжению зависит от направления оси образца относительно о

Сей

кристалла согласно (51.39).

Можно ввести коэффициент тензочувствительности οι по дефо*

мации и вдоль оси. Модулем Юнга Е

, как известно, называют

величину, определяемую соотношением

— р = Е

и, (51.43)

где согласно {51.10)

u = 2

ibWk- (51.44)

Подставляя (51.43) в (51.37), получим

р!1

рП

(1 - ρσχ

)=ρΠ (1 + Е

щи) = ρ» 0 + S/u), ' (51.45)

или

рЧ-рЧ

Необходимо только помнить, что определенный в (51.43) модуль

Юнга Е

зависит от направления. Его можно выразить через тен-

зор модулей упругости согласно (51.25) и (51.10) следующим обра-

зом:

-Ρ = Σι PikKitik = En Σι

imnin

. (51.47)

Выражая p

через u

согласно (51.16), получим

1тЩП

1 U ы

Е„ "Ρ Σ ЬытЩтЩЩ '

ikltn

или

+с

Ю (<S|j+2c

)(c

—Си)

(51.48)

Например, для направления вдоль оси [100], п = (1, 0, 0) полу-

*^(Сп + 2С

>=ЕИоо,. • (51-5°)

чим

£Ю_

li ~

Сц—с

;

Тензочувствительность полупроводников в десятки раз превосх

дит тензочувствительность металлов. Например, для р-

еМ

^п5

с удельным сопротивлением 0,1 Ом-см Si имеет значение около

(тензочувствительность по относительной деформации S

безразмер

величина), что примерно в 60 раз больше соответствующей велики

для проволочных тензометров.

328

§ 52. ТЕНЗОРЕЗИСТИВНЫЙ ЭФФЕКТ.

КОЭФФИЦИЕНТЫ ПЬЕЗОСОПРОТИВЛЕНИЯ

В табл. 16 приведены некоторые экспериментальные данные по

германию и кремнию для коэффициентов пьезосопротивления.

Таблица 16

Адиабатические коэффициенты пьезосопротивления.

(Т = 20°С)

Яп

ι =

ιιιΐ]

рЮ

[111] =

Ро

рЮ

= Ε

[111]

Материал

Ом «см

4111]'

дин/см

= Ε

[111]

(в 10"

см

/дин)

4111]'

дин/см

х π

[111]

Германий:

я-тип 1,5

-2,3 —3,2

—138,1 —94,9

1,55. 1012

—147

Германий:

я-тип

5,7

—2,7

—3,9

—136,8 —94,7

—147

9,9 —4,7 —5,0 — 137,9

—96,9

— 150

16,6

—5,2

—5,5

—138,7

— 101,2

-157

/7-ТИП

1,1

-3,7 3,2

' 96,7

65,4 101,5

15,0

10,6 5,0

46,5 31,4

48,7

Кремний:

15,0

6,6

5,0

46,5

1,87-1012

—.

п-тип

7,8

6,6

—1,1

138,1

•

93,6 175

р-тип

11,7

—102,2 53,4.

— 13,6 —81,3 —142

Табл. 16 показывает, что как коэффициенты пьезосопротивления,

так и тензочувствительность S/ и щ зависят от величины и типа

проводимости, а также от температуры и даже от деформации. Чтобы

понять эти зависимости, необходимо рассмотреть физическую при-

роду тензорезистивного эффекта. В общем случае тензор удельного

сопротивления можно выразить через концентрацию носителей заряда

и тензор подвижности μ:

ρ-ι = βημ = σ. (52.1)

Изменение ρ может быть связано с изменением концентрации

и подвижности:

1. Объемное сжатие. Простейшим случаем тензосопротивле-

ия является случай объемного, или всестороннего, сжатия. Тензор

Деформации вырождается в скаляр ии = и. Постоянная решетки а

ристалла уменьшается "

а' = а

(1-и). (52.2)

Так как расстояние между атомами уменьшается, то увеличива-

ется перекрытие волновых функций электронов, а потенциальная

ергия W (а), описывающая взаимодействие атомов решетки, изме-

лется. Если считать, что минимум W (а) соответствует а = а

, то

(а) возрастает как при сжатии, так и при растяжении кристалла

329

(рис. 76). Учитывая изменение W (а) и области перекрытия волновы*

функций, мы можем прийти к выводу, что меняется как обменный

интеграл A (s), так и величина опускания уровней энергии С, к ото.

рые были введены в теории квазисвязанного электрона. Это приво.

дит в свою очередь к изменению ширины запрещенных зон и зон

энергии.

Но изменение ширины запрещенной зоны должно привести к из-

менени ю концентрации электронов и дырок. Обозначим через β

коэффициент относительного изменения

игц

рины запрещенной зоны при изменении давле-

ния:

о 1 дД£р.

Од Р- ЬЕ

др >

Г 1 Δ£

(ρ) = AEo (1 - βρ). (52.3)

V- j / Если через у обозначить коэффициент

xi/ относительного изменения ширина запрещен-

ной зоны с деформацией:

Рис. 76. Зависимость энер- . dAF

гии взаимодействия ато- у — —:—

мов решетки от расстоя- АЯ

du '

ния между ними

AEq (u) =

Д£

(1 + γιι), (52.4)

то из (52.4), (52.3) и (51.43) можно записать

Р = (52.5)

где Е

—модуль Юнга.

Изменение ширины запрещенной зоны обусловлено тем, что сме-

щается дно зоны проводимости и потолок валентной зоны. При этом

необходимо иметь в виду, что смещение Е

и Ε

может происходить

по-разному. В общем случае положение Е

и Ε

является функцией

относительного изменения объема или тензора деформации:

- £

(U) = £

+§U + I^U4... (52.6)

Ограничиваясь малыми деформациями, можно отбросить все более

высокие степени относительной деформации, кроме первой:

(и) = Е

(0) + А

и. (52.7)

Дополнительная потенциальная энергия электрона в деформиро-

ванной решетке носит название потенциала деформации, а А

назы-

вают постоянной потенциала деформации. Аналогично можно преД'

ставить для потолка валентной зоны

(u) = E

( 0) + A„u. (52.8)

Изменение ширины запрещенной зоны при деформации моЖ*

записать в виде

Δ£

(и) = Е

(и) - Ε

(и) = АЕ (0) + (А

- Α

) и, (52.®

330