Клепко В.Ю., Голець В.Л. Вища математика в прикладах і задачах
Подождите немного. Документ загружается.

51
Розділ I. Лінійна та векторна алгебра
2) сполучний
(
a
+
b
) +
c
=
a
+ (
b
+
c
);
3) для кожного вектора
a
існує протилежний (–
a
), такий, що
a
+ (–
a
) =
0
;
4)
a
+
0
=
a
;
5) для будь+яких двох векторів
a
і
b
виконуються нерівності:
|
a
+
b
|
d
|
a
| + |
b
| ,
|
a
–
b
|
d
|
a
| + |
b
| .
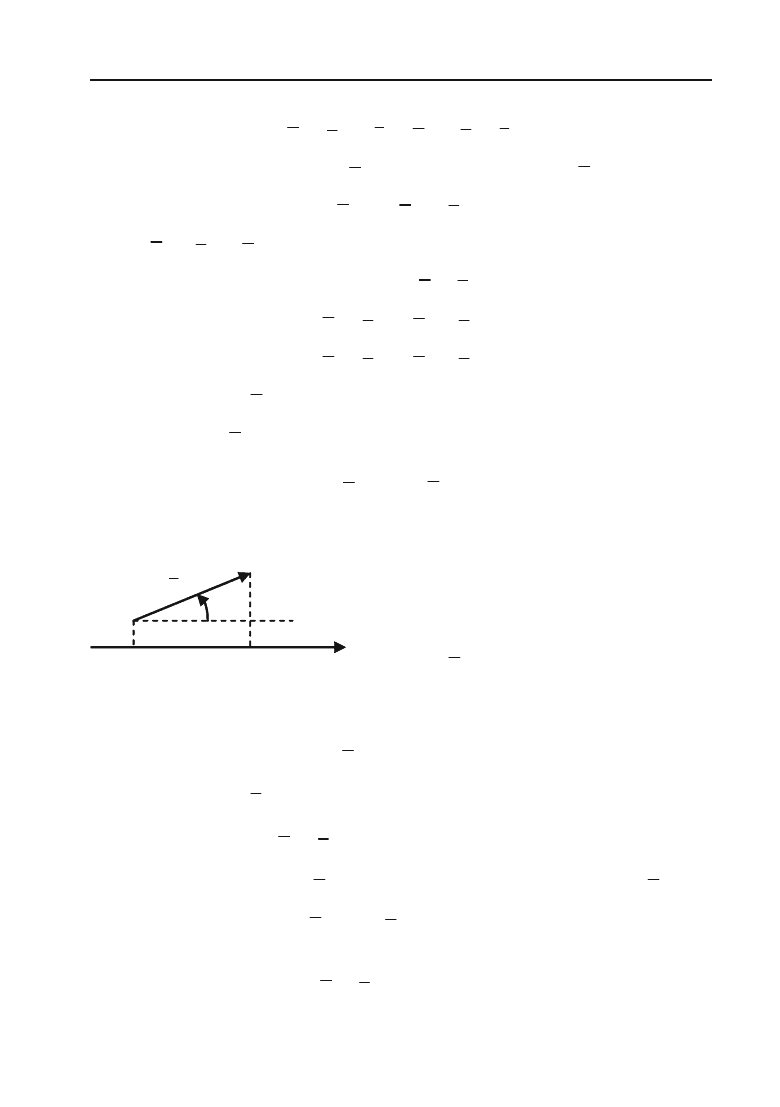
Якщо вектор
a
утворює кут
M
з віссю ОХ (рис. 1.2), то проек,
цією вектора
a
на вісь називається величина
пр
х
a
= а
х
= |
a
|
cos
M
, (1.13)
а
х
= х
2
– х
1
. (1.14)
Нехай вектор має початок у точці
М
1
(х
1
, у
1
, z
1
), а кінець — у точці
М
2
(х
2
, у
2
, z
2
). Тоді величини а
х
= х
2
– х
1
,
а
у
= у
2
– у
1
, а
z
= z
2
– z
1
є проекціями
вектора
a
на осі х, у, z. Проекції век+
тора однозначно визначають вектор.
Тому має місце рівність
a
= {а
х
, а
у
, а
z
}.
Якщо вектор
b
= {b
х
, b
у
, b
z
}, то проекція суми векторів
a
+
b
= {а
х
+b
х
, а
у
+b
у
, а
z
+b
z
}.
Добутком вектора
a
на число
O
називається вектор
a
O
, дов+
жина якого дорівнює |
a
O
| = |
O
||
a
|. Множення вектора на число має
властивість асоціативності та дистрибутивності, тобто для довільних
чисел
O
,
P
та векторів
a
і
b
справедливі рівності:
Рис. 1.2.
a
x
1
a
x
x
2
X
M
52
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1)
O
(
a
P
) =
P
(
a
O
) = (
O
P
)
a
;
2) (
OP
)
a
=
a
O
+
a
P
; (1.15)
3)
O
(
a
+
b
) =
a
O
+
b
O
.
Будь+який вектор
a
= {а
х
, а
у
, а
z
}.
можна записати у вигляді:
a
= а
х
i
+ а
у
j
+ а
z
k
, (1.16)
де
i
,
j
,
k
— одиничні вектори, а
х
i
,
а
у
j
, а
z
k
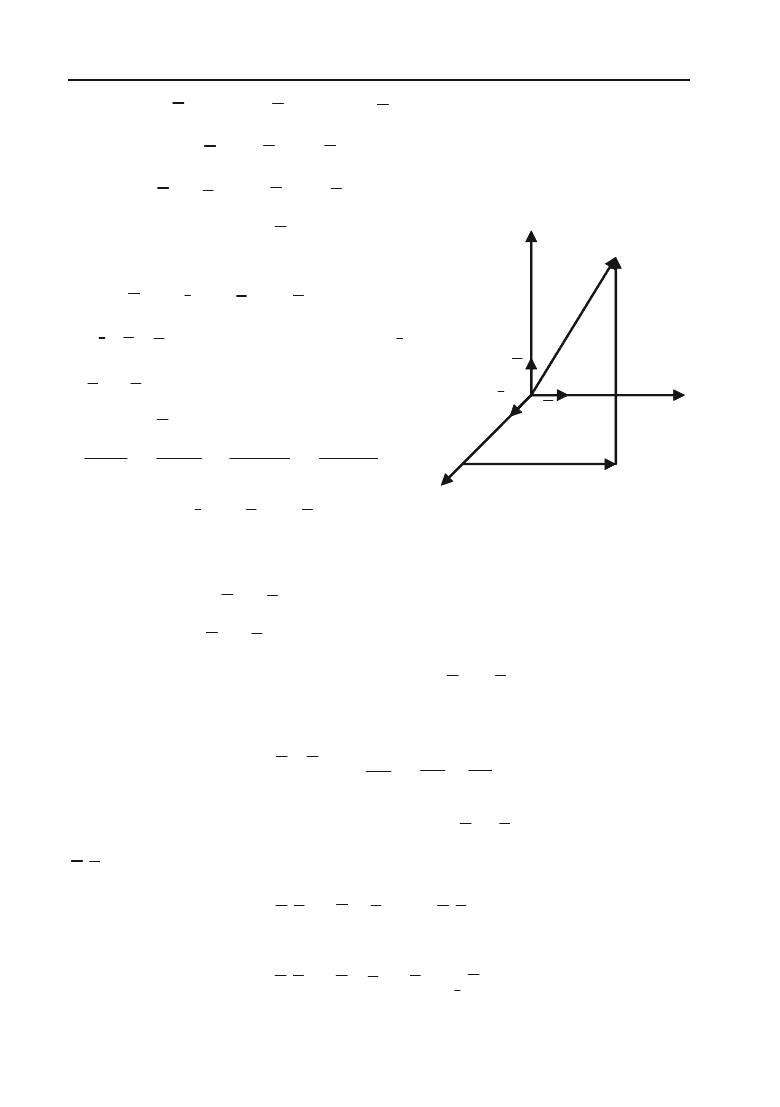
називаються компонентами
вектора
a
(рис. 1.3).
1
OM
=
3
OM
+
32
MM
+
21
MM
=
= а
х
i
+ а
у
j
+ а
z
k
.
Приклад 1.73. Дано два вектори: а = {2; –1; 3} та b = {3; 4; 5}.
Знайти вектор 2
a
–
b
.
Розв’язок. 2
a
–
b
= {2
2 – 3; 2(–1) – 4; 2
3 – 5} = {1; –6; 1}.
Ознакою колінеарності двох векторів
a
та
b
є пропорційність їх
координат:
ab&
x
x
a
b
=
y
y
a
b
=
z
z
a
b
. (1.17)
Скалярним добутком двох векторів
a
і
b
називається число
a
b
, яке дорівнює добутку їх модулів на косинус кута між ними:
a
b
= |
a
|
|
b
|
cos
(
,
ab
). (1.18)
Скалярний добуток можна записати у такому вигляді:
a
b
= |
a
|
b
= |
b
|
b
np
a
.
i
j
k
х
z
у
M
1
M
3
M
2
Рис. 1.3.
53
Розділ I. Лінійна та векторна алгебра
Якщо вектори
a
та
b
задані своїми координатами, то їх скаляр+
ний добуток обчислюється за формулою:
a
b
= а
х
b
x
+ a
y
b
y
+ a
z
b
z
. (1.19)
Враховуючи формули (1.18) і (1.19), можна знайти косинус кута
між векторами
a
і
b
:
cos
(
,
ab
) =
cos
M
=
ab
ab
=
222 222
xx yy zz
x
yz xyz
ab ab ab
aaa bbb
. (1.20)
Звідси випливає умова перпендикулярності двох векторів: якщо
abA
, то
a
b
= 0 або в координатній формі:
а
х
b
x
+ a
y
b
y
+ a
z
b
z
= 0 . (1.21)
Серед властивостей скалярного добутку відмітимо як більш ужи+
вані такі:
1)
a
b
=
b
a
;
2)
a
(
b
+
c
) =
a
b
+
a c
;
3)
O
a
b
=
O
(
a
b
) =
a
O
b
.
Векторним добутком вектора
a
на вектор
b
називається
вектор
c
=
a
u
b
, який має такі властивості:
1) довжина вектора
c
дорівнює добутку довжин співмножників
на синус кута між ними: |
c
| = |
a
|
|
b
|
sin
M
;
2) вектор
c
перпендикулярний до векторів
a
і
b
;
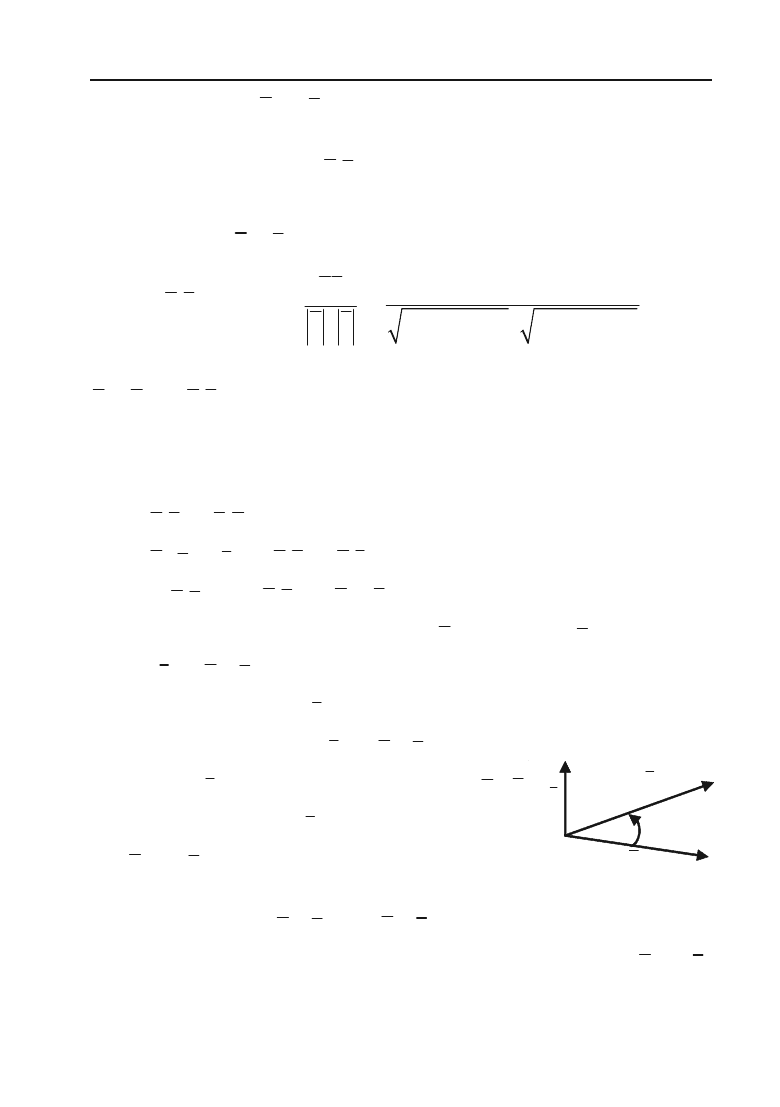
3) з кінця вектора
c
найкоротший поворот
від
a
до
b
уявлявся таким, що відбувається
проти годинникової стрілки (рис. 1.4).
Зауважимо, що [
a
u
b
] = –[
a
u
b
], а модуль векторного добутку
дорівнює площі паралелограма, побудованого на векторах
a
та
b
,
якщо вони віднесені до спільного початку.
Рис. 1.4.
c
b
a

54
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
У координатній формі векторний добуток векторів
a
= {а
х
, а
у
, а
z
}
і
b
= {b
х
, b
у
, b
z
} можна записати у вигляді:
c
=
a
u
b
=
x
yz
x
yz
ijk
aaa
bbb
=
y
z
y
z
aa
bb
°
®
°
¯
; –
x
z
x
z
aa
bb
;
xy
xy
aa
bb
½
°
¾
°
¿
. (1.22)
Мішаним або скалярно,векторним добутком трьох векторів
a
,
b
,
c
називається векторний добуток векторів
a
і
b
, скалярно
помножений на вектор
c
, тобто [
a
u
b
]
c
.
Якщо вектори
a
,
b
,
c
— компланарні, тобто розташовані в одній
площині або на паралельних площинах, то їх мішаний добуток дорів+
нює нулю.
Якщо відомі координати співмножників
a
= {а
х
, а
у
, а
z
},
b
= {b
х
, b
у
, b
z
},
c
= {с
х
, с
у
, с
z
}, то мішаний добуток обчислюється за формулою:
[
a
u
b
]
c
=
x
yz
x
yz
x
yz
aaa
bbb
ccc
. (1.23)
Якщо три ненульових вектора
a
,
b
,
c
розташовані в одній пло+
щині (компланарні), то їх мішаний добуток [
a
u
b
]
c
= 0.
Отже, в координатній формі умова компланарності трьох нену+
льових векторів має вигляд:
x
yz
x
yz
x
yz
aaa
bbb
ccc
= 0.
55
Розділ I. Лінійна та векторна алгебра
1.6.2. Розв’язання прикладів
Приклад 1.74. Задано координати точок М
1
(3; 2; 1), М
2
(–1; 0; 2),
М
3
(–2; –1; 0), та М
4
(5; 7; 3). Знайти:
1) вектор
a
, якщо
a
= 2
12
MM
– 3
34
MM
;
2) кут між векторами
12
MM
та
34
MM
;
3) координати вектора
b
=
12
MM
u
34
MM
;
4) об’єм піраміди з вершинами в точках М
1
, М
2
, М
3
, М
4
.
Розв’язок.
1) За формулою (1.14) знаходимо
12
MM
= {x
2
– x
1
; y
2
– y
1
; z
2
– z
1
} = {–1–3; 0–2; 2–(–1)} = {–4; –2; 3},
2
12
MM
= {–8; –4; 6},
34
MM
= {5–(–2); 7–(–1); 3–0} = {7; 8; 3},
–3
34
MM
= {–21; –24; –9}.
Тоді
a
= 2
12
MM
– 3
34
MM
= {–8–21; –4–24; 6–9} = {–29; –28; –9}.
2) Косинус кута між векторами
12
MM
та
34
MM
обчислимо за
формулою (1.20):
cos
M
=
12 34
12 34
MM MM
MM MM
=
2 22 222
(4)7 (2)8 33
(
4
)(
2
)
3783
=
=
28 16 9
16 4 9 49 64 9
=
35
29 122
|
–0,588.
Оскільки косинус кута від’ємний, то кут
M
тупий.
3) Координати векторного добутку знаходимо за формулою (1.22):
b
=
423
783
ijk
=
i
23
83
–
j
43
73
+
k
42
78
=

56
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
=
i
(–6 – 24) –
j
(–12 –21) +
k
(–32 + 14) =
= –30
i
+ 33
j
– 18
k
= {–30; 33; –18}.
4) Щоб знайти об’єм піраміди, знайдемо спочатку мішаний добу+
ток векторів, що виходять з однієї вершини піраміди:
12
MM
= {–4; –2; 3},
13
MM
= {–5; –3; 1},
14
MM
= {4; 5; 4}.
Тоді об’єм піраміди
V =
1
6
|[
a
u
b
]
c
| =
1
6
423
531
454
=
19
6
= 3
1
6
.
1.6.3. Завдання для самостійної роботи
1.75. Заданими векторами
a
і
b
побудувати вектори: 1) 3
a
;
2) 2
a
+
1
3
b
.
1.76. Дано |
a
| = 13; |
b
| = 19; |
a
+
b
| = 24. Обчислити |
a
–
b
|.
1.77. Дано точки А(3; –1; 2) і В(–1; 2; 1). Знайти координати век+
торів
AB
і
BA
.
1.78. Дано вектори
a
= {2; 2; 1},
b
= {6; 3; 2}. Знайти
a
np b
,
b
np a .
1.79. Знайти кут між векторами
a
=
i
+ 2
j
+ 3
k
,
b
= 6
i
+ 4
j
– 2
k
.
1.80. Знайти одиничний вектор того самого напрямку, що й век+
тор
a
=
i
+ 2
j
+ 2
k
.
1.81. Вектори
a
і
b
взаємно перпендикулярні, причому |
a
| = 5 і
|
b
| = 12. Знайти |
a
+
b
| і |
a
–
b
|.
1.82. Довести, що вектор
p
=
b
(
a
c
) –
c
(
a
b
) перпендикуляр+
ний до вектора
a
.
57
Розділ I. Лінійна та векторна алгебра
1.83. Дано вектори
a
= 3
i
– 6
j
–
k
,
b
=
i
+ 4
j
– 5
k
,
c
=
= 3
i
– 4
j
+ 2
k
. Обчислити
c
np
(
a
+
b
).
1.84. Вектор
x
, компланарний вектору
a
= (6; –8; –7,5), утво+
рює з віссю Oz гострий кут. Знаючи, що
x
= 50, знайти його коор+
динати.
1.85. Знайти довжину вектора
a
= 20
i
+ 30
j
– 60
k
і його на+
прямні косинуси.
1.86. Дано вершини трикутника А(3; 2; –3), В(5; 1; –1) і С(1; –2; 1).
Знайти його зовнішній кут при вершині А.
1.87. Вектори
a
і
b
утворюють кут
M
=
23
S
; знаючи що
|
a
| = 3, |
b
| = 4, обчислити: 1) (3
a
– 2
b
)(
a
+ 2
b
); 2) (
a
–
b
)
2
.
1.88. Дано точки А(–1; 5; –10), В(5; –7; 8), С(2; 2; –7), D(3; –2; 6).
Перевірити, що вектори
AB
і
CD
колінеарні. Знайти який з них
довший і у скільки разів, як вони напрямлені — в один чи в проти+
лежні боки.
1.89. Знайти об’єм V тетраедра з вершинами А(1; 2; 3), В(4; 4; 4),
С(2; 6; 4), D(2; 3; 6).

58
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
1.7.2. Розв’язання прикладів
Приклад 1.90. Визначити власні значення і власні вектори матриці
А =
16
12
§·
¨¸
©¹
.
§1.7. Власні числа та власні вектора
1.6.1. Теоретичні відомості
Вектор+стовпчик X =
1
2
...
n
x
x
x
§·
¨¸
¨¸
¨¸
¨¸
©¹
z
0 називається власним вектором
квадратної матриці А nго порядку, що відповідає власному значенню
O
, якщо він задовольняє матричному рівнянню АX =
O
X, або (А –
O
Е)X = 0.
Тут Е — одинична матриця n+го порядку, а О — нульовий век+
тор+стовпчик. При умові, що X
z
0, одержуємо характеристичне
рівняння для визначення власних значень
O
:
det(A –
O
E) = 0. (1.24)
Координати власного вектора X
і
, що відповідають власному зна+
ченню
i
O
, є розв’язком системи рівнянь:
11 1 12 2 1
21 1 22 2 2
11 22
( ) ... 0,
( ) ... 0,
......................................................
... ( ) 0.
inn
inn
nn nnin
axaxax
ax a x ax
ax ax a x
O
O
O
°
°
®
°
°
¯
(1.25)
Власний вектор визначається з точністю до постійного множника.

59
Розділ I. Лінійна та векторна алгебра
Розв’язок. Характеристичне рівняння даної матриці має вид (1.24):
16
12
O
O
= 0, або
2
340
OO
,
звідки випливає, що матриця А має два власних значення
1
O
= 4 і
2
O
= –1. Власний вектор X
1
, що відповідає
1
O
= 4, визначається з
системи рівнянь виду (1.25)
12
12
(1 4) 6 0
(2 4) 0
xx
xx
®
¯
, або
12
12
36 0
20
xx
xx
®
¯
,
яке зводиться до одного рівняння х
1
= 2х
2
.
Поклавши х
2
= t, одержуємо розв’язок у вигляді х
1
= 2t, х
2
= t.
Отже, перший власний вектор є
X
1
=
2
1
§·
¨¸
©¹
t.
Другий вектор X
2
, що відповідає власному значенню
2
O
= –1,
визначається з системи рівнянь виду (1.25)
12
12
(1 1) 6 0
(2 1) 0
xx
xx
®
¯
.
Ця система рівнянь також зводиться до одного рівняння х
1
+ 3х
2
= 0;
поклавши х
2
= С, запишемо її розв’язок у вигляді х
1
= –3С, х
2
= С.
Отже, другий власний вектор є
X
2
=
3
1
§·
¨¸
©¹
С.
Таким чином, матриця А має два різних власних значення
1
O
= 4
і
2
O
= –1 і два власних вектора, рівних X
1
=
2
1
§·
¨¸
©¹
і X
2
=
3
1
§·
¨¸
©¹
(з
точністю до постійного множника).

60
Клепко В.Ю., Голець В.Л. «Вища математика в прикладах і задачах»
Приклад 1.91. Знайти власні вектори і власні значення матриці
А =
20 1
11 1
10 2
§·
¨¸
¨¸
¨¸
©¹
.
Розв’язок. Характеристичне рівняння
20 1
11 1
10 2
= 0.
Розкривши визначник отримаємо:
(1 –
O
)[(2 –
O
)
2
– 1] = 0,
(1 –
O
)(1 –
O
)(3 –
O
) = 0,
(1 –
O
)
2
(3 –
O
) = 0,
1
O
=
2
O
= 1,
3
O
= 3.
Корінь
1
O
= 1 — кратний, показник кратності r = 2, корінь
3
O
= 3 — простий, r = 2.
Система рівнянь для визначення власних векторів має вигляд:
13
123
13
(2 ) 0,
(1 ) 0,
(2 ) 0.
xx
xxx
xx
O
O
O
°
®
°
¯
Послідовно підставимо
1
O
і
3
O
в записану систему:
1)
1
O
= 1, r = 2:
13
13
13
0,
0,
0.
xx
xx
xx
°
®
°
¯
^
13
= 0xx
,
^
13
x
x
.
