Конверський А. Є. Логіка (традиційна та сучасна)

Подождите немного. Документ загружается.

Книга друга. СУЧАСНА ЛОГІКА

381

Відомо, що закон у логічній теорії є формула, яка істинна

при будь-яких прийнятих у цій теорії інтерпретаціях нелогі-

чних термінів, що входять до складу цієї формули.

У логіці предикатів інтерпретація нелогічних символів

здійснюється вибором деякої моделі <U,I> і приписуван-

ням значень предметним змінним ϕ.

Дефініція логічного закону: «Формула А є законом

класичної логіки предикатів, якщо і тільки якщо А

приймає значення «істина» в кожній моделі і при будь-

якому приписуванні значень предметним змінним».

Закони логіки ще називають загальнозначимими фор-

мулами. Позначають їх символом |=А.

Прикладом загальнозначимої формули є вираз:

∀х Р(х) ⊃ ∃х Р(х).

Обгрунтуємо загальнозначимість цієї формули. Для цьо-

го застосуємо метод від супротивного.

Припустимо, що ∀х Р(х) ⊃ ∃х Р(х) не є загальнозначи-

мою формулою. А це означає, що існує модель <U,I> і

приписування ϕ, при яких

| ∀х Р(х) ⊃ ∃х Р(х) | = х.

Це означає, що

∀х Р (х)

= і і

∃х Р(х)

= х при ϕ.

Істинність ∀х Р(х) означає, що

Р(х)

= і при припису-

ванні х будь-якого індивіду із U. Хибність ∃х Р(х) означає,

що

Р(х)

= х при приписуванні х будь-якого індивіду із

U. Візьмемо довільний елемент ν із U.

Згідно з вищезазначеним

Р(х)

= і при приписуванні х

індивіда ν і одночасно

Р(х)

= х при цьому самому при-

писуванні. Отже, ми прийшли до протиріччя. Цим і вста-

новлюється загальнозначимість формули

∀х Р(х) ⊃ ∃х Р(х).

Дефініція незагальнозначимої формули. «Формула А

не є законом логіки предикатів тоді і тільки тоді, коли

існує модель і існує приписування предметним змінним,

при яких А приймає значення «хиба».

Щоб показати незагальнозначимість формули, потрібно

вибрати модель <U,I> і приписування ϕ, при яких ця фо-

рмула прийме значення «хиба».

Візьмемо для прикладу формулу:

∃х Р(х) ⊃ ∀х Р(х)

А. Є. Конверський. ЛОГІКА

382

і покажемо її незагальнозначимість. За область інтерпре-

тації U візьмемо множину хімічних елементів. Нехай ін-

терпретаційна функція співставляє предикаторній конста-

нті Р множину металів. Приписування предметним змін-

ним ϕ може бути довільним, оскільки дана формула є за-

мкненою.

Якщо змінній х приписати ім’я «Мідь», то в моделі

<U,I> формула Р(х) буде істинною. Якщо ж змінній х

приписати ім’я «Кисень», то Р(х) виявиться хибною фор-

мулою. Отже, існує приписування змінній х, при якому

| Р(х) | = і,

звідси випливає, що

| ∃х Р(х) | = і при довільному ϕ.

І разом з тим є й друге приписування х, при якому

| Р(х) = х,

а це означає, що

| ∀х Р(х) | = х при ϕ.

Істинність ∃х Р(х) і хибність ∀х Р(х) в <U,I> при ϕ сві-

дчить, що

| ∃х Р(х) ⊃ ∀х Р(х) | = х при ϕ.

Отже, дана формула незагальнозначима.

Дефініція виконуваної формули: «Формула А мови

логіки предикатів є виконуваною», якщо і тільки якщо існує

модель і приписування значень предметним змінним,

при яких А приймає значення «істина».

Звернемося до прикладу.

Ми встановили, що формула ∃х Р(х) ⊃ ∀х Р(х) є незага-

льнозначимою. Тепер покажемо, що вона є виконуваною.

Для цього виберемо модель <U,I> і приписування ϕ, при

яких ця формула буде істинною. Функція І співставляє Р

порожню множину (наприклад, множину людей, які є жи-

телями Місяця), ϕ знову є довільним. Зрозуміло, що Р не

має жодного елементу.

Тому, | Р(х) | = х при приписуванні х будь-якого об’єкту

із U, а звідси випливає, що | ∃х Р(х) | = х при ϕ. Але якщо

антецедент нашої формули хибний, то вся формула буде

істинною:

Книга друга. СУЧАСНА ЛОГІКА

383

| ∃х Р(х) ⊃ ∀х Р(х) | = і при ϕ.

Отже, формула є виконуваною.

Дефініція невиконуваної формули: «Формула є невико-

нуваною тоді і тільки тоді, коли вона приймає значен-

ня «хиба» в кожній моделі і при кожному приписуванні

значень предметним змінним».

Візьмемо для прикладу формулу:

 ∃х Р(х) ∧ Р(а).

Застосуємо міркування від супротивного. Будемо ствер-

джувати, що дана формула виконувана. Тоді повинна існу-

вати модель <U,I> і приписування ϕ, при яких вона істин-

на. Наша формула є кон’юнкцією. А це означає, що

|  ∃х Р(х) | = і і | Р(а) | = і при ϕ.

Істинність Р(а) свідчить про те, що І (а)

∈

І (Р).

А істинність  ∃х Р(х) означає хибність ∃х Р(х).

Визнання цього факту означає, що | Р(х) | = х при при-

писуванні будь-якого елемента із U, до речі, і того, який

функція І співставляє константі а.

Отже, | Р(х) | = х при приписуванні х об’єкта І (а).

Тоді ми повинні визнати, що І(а)

∉

І(Р). Але це супере-

чить прийнятому раніше твердженню, що: І(а)

∈

І(Р).

Отже, припущення про виконуваність формули  ∃х Р(х)

∧ Р(а) неправильне. Дана формула не є виконуваною.

5. Логічні відношення між формулами в S

До фундаментальних відношень у класичній логіці

предикатів відносять:

 відношення сумісності за істинністю,

 відношення сумісності за хибністю і

 відношення логічного слідування.

Дефініція І: «Формули Γ сумісні за істинністю, якщо

і тільки якщо існує модель і приписування значень

предметним змінним, при яких кожна формула із Γ

приймає значення «істина». У протилежному випадку

ці формули несумісні за істинністю».

А. Є. Конверський. ЛОГІКА

384

Дефініція П: «Формули Γ сумісні за хибністю, якщо і

тільки якщо існує модель і приписування змінним, при

яких кожна формула із Γ приймає значення «хиба». У

протилежному випадку ці формули несумісні за хибні-

стю».

Проілюструємо наведені дефініції на прикладі.

Візьмемо формули:

∃х R(x,y) i ∃x  R(x,y)

і покажемо, що вони сумісні за істинністю.

Для цього достатньо вибрати конкретну модель <U,I> і

конкретне приписування ϕ, при яких обидві формули разом

будуть істинні.

За універсум розгляду приймемо множину міст U. Не-

хай І співставляє двомісній предикаторній константі R

множину таких пар міст, перше із яких південніше друго-

го Функція ϕ приписує вільній предметній змінній у місто

Київ, а решті змінним – довільні міста.

Розглянемо тепер приписування ϕ, яке у також співставляє

Київ, а х Одесу. Оскільки Одеса південніше Києва, то пара <

Одеса, Київ

міститься в I(R) і означає | R(x,y) | = i при ϕ.

А звідси випливає, що | ∃х R(x,y) | = i при ϕ.

Розглянемо тепер приписування ϕ, яке знову співстав-

ляє у – Київ, a х – Львів. Оскільки Львів розташований

не південніше Києва, то пара <Львів, Київ

не міститься в

І(R) i | R(x,y) | = x при ϕ.

Тоді, |  R(x,y) | = i при ϕ. Звідси випливає | ∃x  R(x,y) | =

= i при ϕ.

Отже, формули ∃х R(x,y) i ∃x  R(x,y) y моделі <U,I> і

при приписуванні ϕ одночасно приймають значення «іс-

тинa», що свідчить про їх сумісність за істинністю.

Візьмемо ту саму модель <U,I> і приписування ϕ. По-

кажемо, що формули ∀х  R(x,y) i ∀x R(x,y) сумісні за хи-

бністю.

У попередньому прикладі ми встановили, що | R(x,y) | =

i при ϕ. Звідси випливає, що |  R(x,y) | = x при ϕ.

Тоді ∀x  R(x,y) = x при ϕ. Також було встановлено, що

| R(x,y) | = x при ϕ. А це означає, що ∀х R|x,y| = x при ϕ.

Виходить, що в даній моделі при даному приписуванні

формули

∀х  R(x,y) i ∀x R(x,y) сумісні за хибністю.

Книга друга. СУЧАСНА ЛОГІКА

385

За допомогою досить простих міркувань можна показа-

ти, що формули:

а) ∀х  R(x,y) i ∀x R(x,y) є несумісними за істинністю,

б) ∃x R(x,y) i ∃x  R(x,y) є несумісними за хибністю.

1. Щоб показати несумісність за істинністю формул

∀x  R(x,y) i ∀x R(x,y),

зробимо припущення про їх сумісність за істинністю. Тоді,

|  R(x,y) | = i i | R(x,y) | = i.

Але визнання істинності формули |  R(x,y) | змушує

вкзати на хибність формули | R(x,y) |. Отже, ми маємо про-

тиріччя.

2. Для встановлення несумісності за хибністю формул

∃х R(x,y) i ∃x  R(x,y)

зробимо припущення, що вони сумісні за хибністю при де-

якій моделі <U,I> і при приписуванні ϕ.

Якщо це так, то | R(x,y) | = x i |  R(x,y) | = x.

Але визнання хибності формули |  R(x,y) | приму-

шує визнати істинність формули | R(x,y) |. Маємо проти-

річчя.

Отже, вихідні формули за хибністю несумісні.

Виходить, що формули ∀х  R(x,y) i ∀x R(x,y) знахо-

дяться у відношенні протилежності, оскільки вони сумі-

сні за хибністю і несумісні за істинністю, а формули ∃х

R(x,y) i ∃x  R(x,y) перебувають у відношенні підпроти-

лежності, оскільки вони сумісні за істинністю і несумісні

за хибністю.

Дефініція Ш. Із множини формул Γ логічно слідує

формула В (Γ |= В), якщо і тільки якщо не існує моделі і

приписування значень предметним змінним, при яких

кожна із формул Γ приймає значення «істина», а фор-

мули В – значення «хиба».

Проілюструємо наведену дефініцію на прикладі.

Покажемо, що із Р(а) і Q(a) логічно слідує ∃x (P(x) ∧

∧ Q(x)).

P(a), Q(a) |= ∃x (P(x) ∧ Q(x)).

Припустимо, що Р(а) і Q(a) не слідує із ∃x (P(x) ∧ Q(x)):

P(a), Q(a)  |= ∃x (P(x) ∧ Q(x)).

А. Є. Конверський. ЛОГІКА

386

Якщо це так, то існує модель <U,I> і приписування ϕ,

при яких Р(а) і Q(a) – істинні, а ∃х (P(x) ∧ Q(x)) – хибна.

Істинність Р(а) і Q(a) означає, що І(а) ∈ І(Р) і І(а) ∈

∈ І(Q).

Тому, якщо довільній предметній змінній х приписати

об’єкт І(а), то

|P(x)| = i i |Q(x)| = i.

Звідси виходить, що |P(x) ∧ Q(x)| = i при приписуванні х

значення І(а). Виходить, | ∃x (P(x) ∧ Q(x)) | = i при припи-

суванні ϕ, але це суперечить нашому припущенню.

Отже, із формул P(a) i Q(a) логічно слідує формула ∃х

(P(x) ∧ Q(x)).

6. Проблема розв’язання

Визначення поняття закону класичної логіки предика-

тів (загальнозначимої формули) і логічного слідування в

логіці предикатів передбачає відповідь на такі запитання:

а) За допомогою якої процедури можна встановити чи є

деяка формула А законом чи ні?

б) За яких умов із формул А

, А

, ..., А

слідує формула В ?

У класичній логіці висловлювань самі визначення логі-

чного закону і логічного слідування містять вказівку на

перевірочну процедуру, яка дозволяє встановити чи є дана

формула законом, і чи слідує із формули А

, А

, ..., А

фо-

рмула В.

Тобто, щоб встановити чи є формула А законом, необ-

хідно у відповідності з визначенням тотожно-істинної фор-

мули побудувати таблицю істинності для А і з’ясувати, чи

приймає А значення «і» в усіх рядках таблиці.

А для відповіді на запитання чи слідує формула В із А

,..., А

, необхідно у відповідності з визначенням логічно-

го слідування в класичній логіці висловлювань, побудува-

ти спільну таблицю істинності для формул А

, А

,..., А

і В

і з’ясувати, чи є в цій таблиці рядок, коли А

, А

,..., А

приймає значення «і», а для В значення «х».

Оскільки процес побудови таблиць істинності є алгори-

тмічним, то перевірити, чи є довільна формула логіки ви-

словлювань її законом (а також чи має місце відношення

логічного слідування між формулами А

, А

,..., А

і В), мо-

Книга друга. СУЧАСНА ЛОГІКА

387

жна кінцевою кількістю кроків. Ті логічні теорії, в яких

це можна здійснити, називаються розв’язуваними.

Дефініція: «Логічна теорія називається розв’язуваною,

якщо існує ефективна процедура (алгоритм), що дозво-

ляє для будь-якої формули кінцевим числом кроків ви-

рішити питання про те, чи є ця формула законом тео-

рії чи ні».

Класична логіка висловлювань є розв’язуваною. Цього

не можна сказати про класичну логіку предикатів. Визна-

чення в ній закону і логічного слідування не є ефектив-

ним, тобто не містить алгоритму вирішення питання про

загальнозначимість довільної формули А і наявності від-

ношення логічного слідування між довільними формулами

, А

, ..., А

і В.

Справді, щоб встановити загальнозначимість формули А,

необхідно розглянути всі моделі і всі приписування зна-

чень предметним змінним і переконатися, що в кожному

випадку А приймає значення «істина». А для того, щоб

показати, що А

, А

,..., А

|= В слід розглянути всі моделі і

всі приписування і переконатися, що відсутня ситуація,

коли А

, А

,..., А

приймають значення «істина», а В –

значення «хиба».

Зрозуміло, що подібний підбір і перегляд yсіх моделей і

приписувань неможливий через те, що цей процес нескін-

ченний (на відміну від числа рядків будь-якої таблиці іс-

тинності), оскільки в ньому відсутній алгоритм роз-

в’язання питання про загальнозначимість формули і від-

ношення слідування між формулами. Розв’язання цих пи-

тань у логіці предикатів є евристичним завданням.

Разом з тим у класичній логіці предикатів розроблено

ряд процедур, які дозволяють стандартним і досить опти-

мальним засобом підійти до проблеми розв’язування.

Зупинимося на одній із них. А саме на процедурі, яка

отримала назву «метод аналітичних таблиць».

Суть цього методу полягає в тому, що теза про за-

гальнозначимість формули А і теза про слідування фо-

рмули В із А

, А

,...,А

обгрунтовуються способом мір-

кування від супротивного.

Наприклад, для обгрунтування тези «|=А», показують,

що припущення хибності А з необхідністю приводить до

протиріччя. Для обгрунтування тези «А

, А

,..., А

|= В»

А. Є. Конверський. ЛОГІКА

388

показують, що припущення істинності А

, А

,..., А

і хи-

бності В приводить до протиріччя.

Введемо деякі пояснення щодо побудови самої аналі-

тичної таблиці. Процес міркування від супротивного,

який обгрунтовує одну із названих тез, оформлюється

у вигляді деякої послідовності кроків, яку називають

аналітичною таблицею.

 Кожен крок в аналітичній таблиці відображає за-

стосування відповідного аналітичного правила;

 кроки складаються із рядків, які є результатами

дії відповідних аналітичних правил;

 кроки позначають римськими цифрами (І, П, Ш

тощо);

 рядки – арабськими цифрами (1, 2, 3 тощо);

 нумерація рядків аналітичної таблиці починаєть-

ся з нуля (0). Цим підкреслюється, що ми починаємо

будувати аналітичну таблицю із антитези;

 вся таблиця від нульового рядка до останнього

розбивається на гілки;

 перехід від одного кроку в аналітичній таблиці до

іншого здійснюється за допомогою спеціальних аналі-

тичних правил, в основі яких лежать смисли пропози-

ційних зв’язок ∧, ∨, ⊃, ∾,  і кванторів ∀ і ∃;

 кожному із цих правил приписується індекс Т

(«істина») і F («хиба»).

Мета побудови аналітичної таблиці полягає в тому, щоб

показати, що антитеза приводить до протиріччя.

Якщо в гілці є формула С із обома індексами Т і F, то

така гілка вважається замкненою. А якщо в кожній гі-

лці зустрічається деяка формула із індексами Т і F, то

вся таблиця є замкненою.

При отриманні такого результату теза про загальнозна-

чимість формули А або ж про слідування В із А

, А

, ...,

вважається обгрунтованою.

Визначення аналітичних правил

BTA

∧

FBFA

BFA

∧

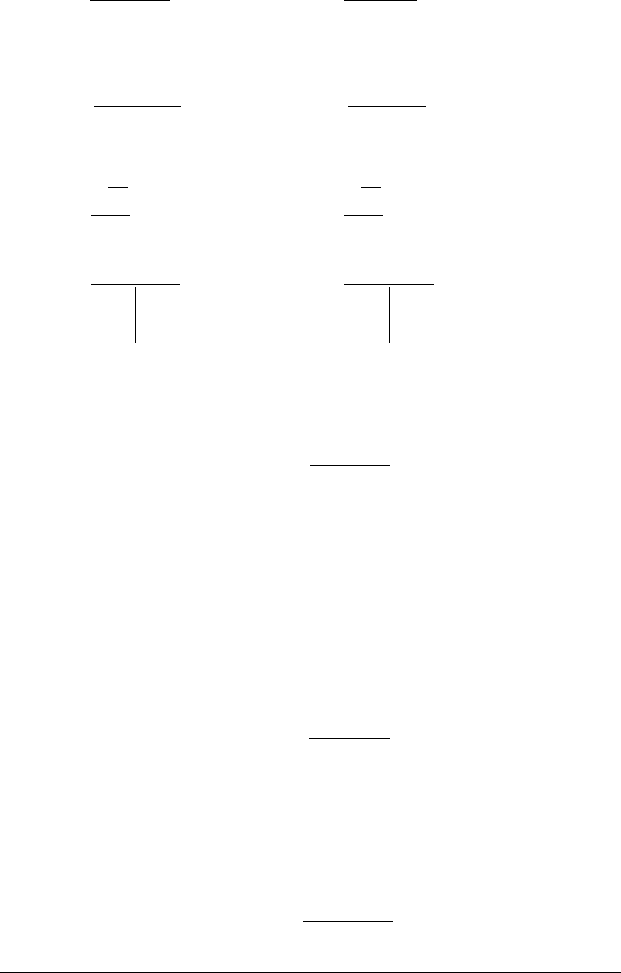
Книга друга. СУЧАСНА ЛОГІКА

389

TBTA

BTA

∨

BFA

∨

TBFA

BTA

⊃

BFA

⊃

FBTB

FATA

BTA

TBFB

FATA

BFA

Аналітичні правила для ∀ і ∃ супроводимо деякими по-

ясненнями.

()

aTA

xAT

∀

де а – будь-яка предметна змінна.

У відповідності з логічним смислом квантора загально-

сті формула ∀х А(х) істинна якщо і тільки якщо будь-

який індивід предметної області задовольняє умові

А(х). Тому у випадку істинності ∀х А(х) істинною вияв-

ляється будь-яка формула виду А(а), яка є результатом

заміни всіх вільних входжень х в А на довільний замкне-

ний терм а.

()

вFA

xAF

∀

де в – предметна змінна, яка не зустрічається в жодній із

попередніх формул гілки, де це правило застосовується.

Хибність формули ∀х А(х) означає існування об’єкта,

який не задовольняє умову А(х):

()

вTA

xxAT

∃

А. Є. Конверський. ЛОГІКА

390

Відповідно до смислу квантора ∃ істинність ∃х А(х)

означає існування об’єкта, що задовольняє умову А(х).

()

aFA

xxAF

∃

Хибність формули ∃х А(х) означає, що будь-який ін-

дивід предметної області не задовольняє умову А(х).

Сформулюємо, як підсумок зазначеному, критерії зага-

льнозначимості і логічного слідування.

Дефініція: Формула А загальнозначима |= А, якщо і

тільки якщо існує замкнена аналітична таблиця, нульо-

вий рядок якої представлений антитезою А».

Дефініція: «Із формули А

, А

,..., А

логічно слідує фор-

мула В, якщо і тільки якщо існує замкнена аналітична

таблиця, нульовий рядок якої представлений виразом

, А

,..., А

 |= В.

При побудові аналітичної таблиці необхідно до-

тримуватися певних вказівок, які полегшують її побу-

дову.

1. Із множини аналітичних правил насамперед засто-

совують пропозиційні аналітичні правила, а потім –

кванторні правила Т∀, F∀

T∃

F∃.

2. Із кванторних правил спочатку застосовують

правила F∀ i T∃, які вимагають введення нових пред-

метних констант, а потім – правила Т∀ і F∃, які не

містять обмежень на терм, що підставляється на міс-

це підкванторної змінної.

Звернемося до прикладу.

І. Необхідно методом аналітичних таблиць обгрунтувати

тезу:

Р(а) ∨ Q(в), Q(в) ⊃ R(с) |

R(с) ∨ P(a)

0. F [P(a) ∨ Q (в) ∧ (Q(в) ⊃ R(с))] ⊃ (R(с) ∨ P(a))

І. 1. Т (P(a) ∨ Q (в)) ∧ (Q(в) ⊃ R(c))

2. F (R(c) ∨ P (a)) F ⊃ до 0

ІІ. 3. Т (Р(а) ∨ Q(в))

4. Т (Q(в) ⊃ R(c)) T ∧ до 1

Як і у логіці висловлювань у таких випадках засновки об’єднують через

«∧» і до них через «⊃» приєднують висновок.