Kopnin N.B. Theory of Nonequilibrium Superconductivity

Подождите немного. Документ загружается.

where the total-energy current is

8.5 The Keldysh diagram technique

8.5.1 Definitions of the Keldysh functions

We have already mentioned that it is the absence of the proper time-ordering

procedure in the definitions of the real-time Green functions that produces

practical difficulties with calculations of the real-time functions. However, one

can establish the necessary time-ordering for some auxiliary Green functions in

such a way that the Wick theorem works for them. After the Wick theorem is

restored, one can derive the Dyson equation (or to formulate the diagram

technique) thus providing the algorithm of calculating these auxiliary Green

functions. The next step is to relate the auxiliary functions to the true real-time

Green functions or to express the physical observables through some of the

auxiliary Green functions (Keldysh 1964). In this section we discuss the

correspondence between the method of the analytical continuation and the

Keldysh technique. We shall see that the both methods lead to the same results:

The equations for the Green functions which determine the physical observables

are identical in the both cases. One can use any of these two methods. Since we

have already derived the basic equations using the method of analytical

calculation, we discuss the Keldysh approach only briefly for the most simple

case. A more detailed description of the Keldysh technique can be found in the

review by Rammer and Smith (1986).

end p.163

Let us consider the statistical average of a single-particle-observable operator

which is linear in the particle-field operators

in the Heisenberg

representation as introduced in Section 2.1. It contains the average

where (1) is the Heisenberg operator

defined through the S-matrix introduced by eqn (2.63):

It is assumed that the system was in equilibrium at t = t

and had a temperature

T. We put t

= – assuming that the nonequilibrium interaction is turned on at

= – . We see that the operators depend on times which are confined to the

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共6页 2010-8-8 15:46

interval ranging from – up to the largest time max {t

, t

}. Moreover, the time

instants belonging to the operator

are not ordered with respect to the instants

which belong to the operator

. We want to relate this average to the average

of a sequence of operators whose times are fully ordered with respect to each

other. The proper ordering is achieved along the time contour depicted in Fig.

8.5. It starts at –

and runs up to the largest time max {t

, t

} and then

returns back to the time –

. We denote the ordering along this contour by T

and define the auxiliary Green function

(8.66)

The time-ordering T

orders the operators as follows

The relation t

means that t

is later than t

along the contour c. The

contour c is shown in Fig. 8.5(a) for t

The upper sign refers to Fermi

particles while the lower sign is for the Bose particles. The brackets denote the

statistical average.

We introduce also the other auxiliary functions

end p.164

FIG. 8.5. The Keldysh time contours for real-time ordered Green

functions.

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共6页 2010-8-8 15:46

One can see that

We can extend the contour c up to + by introducing the identical unity

under the averaging in eqn (8.68). The contour c transforms into the contour C

which consists of two parts: the contour C

runs from – to + and the contour

which runs back from + to – . The contour C is shown in Fig. 8.5(b).

The physical observables are expressed through the function

. For

example, the Fermionic density is

(8.67)

where the sum is over the spin indices. At the same time, it is the contour-

ordered Green function G in eqn (8.66) that possesses a simple perturbative

expansion. Indeed, we can prove the Wick theorem for the average of the

contour-ordered particle operators exactly in the same way as it was done for

averages of the imaginary-time ordered operators. We want now to establish a

connection between G

and the time-ordered function G.

Let us now construct the matrix in the so-called Keldysh space

(8.68)

whose components are defined as follows

end p.165

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第6页共6页 2010-8-8 15:46

(8.69)

The time-ordering operator T

is the usual time-ordering along the contour C

and the operator orders along the contour C

, i.e., it is the “inverse-time”

ordering in the usual sense

It is convenient, however, to use another representation of the matrix Green

function which is obtained from eqn (8.68) by a linear transformation. The point

is that the four components in eqn (8.69) are not linearly independent. Indeed,

we observe that

We introduce here the retarded and advanced Green functions G

and G

respectively, defined in the usual way

and

The function G

is defined as

(8.70)

It is called the Keldysh function. Performing the transformation

where

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [166]-[170]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共5页 2010-8-8 15:49

we arrive at the matrix Green function

(8.71)

Equation (8.71) is the standard representation accepted in the literature.

end p.166

The physical observables can be expressed through the Keldysh function. Indeed,

using the identity

which follows from the general commutation rules eqn (2.15) we find from eqn

(8.70)

(8.72)

Let us calculate the particle density using eqn (8.67). We write N = N

+ N

where N

is the density for noninteracting particles. We have

In the frequency representation

we get

This expression coincides with eqn (8.30) obtained by the analytical continuation

of the Matsubara Green function.

8.5.2 Dyson equation

Consider a series expansion, for the simplest example of the interaction, with the

external potential U. The first-order diagram of the type shown in Fig. 8.1 gives

for the contour-ordered Green function

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共5页 2010-8-8 15:49

The integral along the contour C can be separated into the integrals along C

and

. Interchanging the limits of integration on the lower contour C

we present.

(1)

as the sum of two terms which can be written as components in the Keldysh

space

(8.73)

where we introduce the matrix

end p.167

and assume summation over repeated indices. Equation (8.73) can be written in

the matrix form

where we assume integration, over internal coordinates and time. It is now clear

that collecting all orders of the perturbation expansion in U we arrive at the

Dyson equation for the full Green function

(8.74)

One can easily check that eqn (8.74) transforms into

(8.75)

for the matrices in the representation of eqn (8.71). The potential U is

proportional to the unit matrix in the Keldysh space.

We introduce now the inverse operator for the Green function of noninter-acting

particles

Applying the inverse operator to eqn (8.75) we obtain the Dyson equation in the

differential form

The interaction with impurities, phonons, and electron electron–interact ions can

also be included into the same scheme. These interactions introduce the

corresponding self-energies which also are Keldysh matrices:

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第3页共5页 2010-8-8 15:49

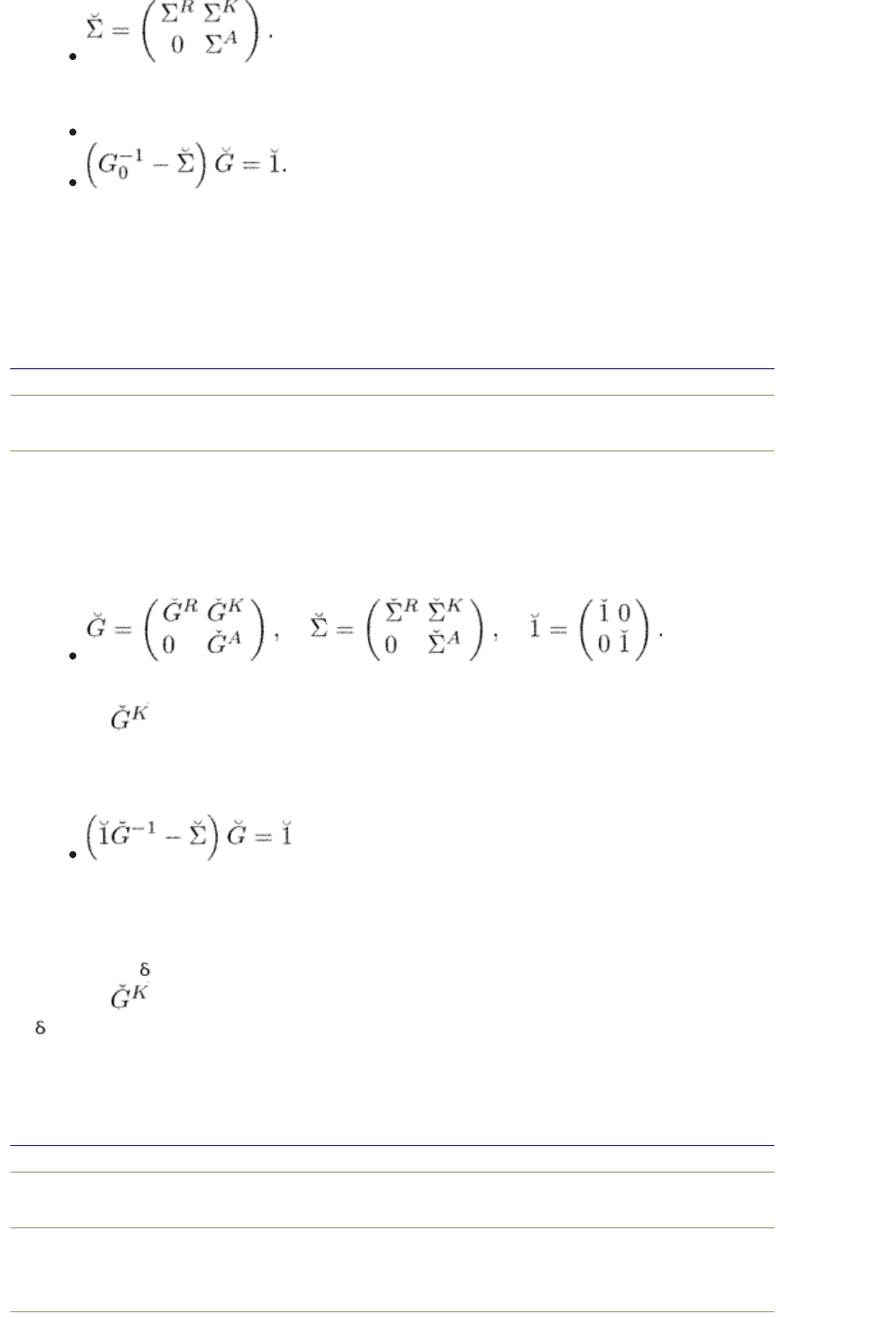
The resulting Dyson equation takes the form

(8.76)

We do not specify the rules as to how to construct the elements of these matrices

within the Keldysh formalism: they are the same as those obtained using the

method of analytical continuation. The detailed description of the Keldysh

formulation of various interactions can be found in the review by Rammer and

Smith (1986).

end p.168

8.5.3 Keldysh functions in the BCS theory

We have four different Green functions in the BCS theory. Accordingly, the

components of the matrix in the Keldysh space used in the BSC theory are

matrices in the Nambu space. We define the Keldysh matrices

From eqns (8.20) and (8.24) or eqn (8.27) one can directly see that the total

function

introduced as a result of analytical continuation of the Matsubara

Green functions is nothing but the Keldysh function because it satisfies the same

equations. Indeed, instead of two equations (8.20) and one equation (8.24) we

obtain one matrix equation

which is a generalization of eqn (8.76).

The expressions for the order parameter and for the current density in terms of

the Keldysh functions are the same as obtained by the analytical continuation.

Indeed, the

-tern in eqn (8.72) is absent for the F-component of the Keldysh

function

. This directly results in eqn (8.28) for the order parameter. The

-term also disappears if one applies the momentum operator to the function G

when calculating the current. As a result, eqn (8.29) is reproduced as well. We

thus have confirmed that the method of analytical continuation and the Keldysh

method are completely equivalent.

end p.169

9 QUASICLASSICAL METHOD FOR NONSTATIONARY

PHENOMENA

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第4页共5页 2010-8-8 15:49

Nikolai B. Kopnin

Abstract: This chapter applies the quasiclassical approximation to nonstationary

problems in the theory of superconductivity. The Eliashberg equations for the

quasiclassical Keldysh Green functions are derived. Normalization of the Green

functions in nonequilibrium situation is found. The Keldysh function is expressed

in terms of a two-component generalized distribution function. The diffusive limit

in nonstationary superconductivity is described. An example of stimulated

superconductivity due to microwave irradiation is considered: the order

parameter becomes enhanced as a result of a depletion of nonequilibrium

distribution of excitations in the energy range of the superconducting gap.

Keywords: Eliashberg equations, Keldysh function, normalization,

distribution function, stimulated superconductivity

We apply the quasiclassical approximation to nonstationary problems in the

theory of superconductivity and derive the Eliashberg equations for the

quasiclassical Green functions. We express the Keldysh function in terms of

a generalized two-component distribution function. As an example, we

consider a nonlinear response of a superconductor to microwave

irradiation: tin order parameter becomes enhanced as a result of a

nonequilibrium distribution of excitations under irradiation.

9.1 Eliashberg equations

The quasiclassical method based on the fundamental assumption that the Fermi

momentum is larger than the inverse coherence length can be applied to

non-stationary problems, as well. As in Chapter 5, this assumption again allows

us to consider the Green functions only in a vicinity of the Fermi surface. As in

the static case, we introduce the quasiclassical matrix Green function integrated

over the energy variable d

. In addition to

R(A)

we define

and similarly for

(a)

The momentum p

lies at the Fermi surface; its magnitude

is fixed, thus the Green function only depends on the direction of the

momentum. One can obtain equations for the quasiclassical functions using the

corresponding transport-like equations derived in the previous section in a full

analogy to the static case.

We start the derivation of the quasiclassical equations with an important

observation that the transport-like equation (8.60) does not contain

explicitly.

Within the quasiclassical approximation, the Hamiltonian contains v

taken at

the Fermi surface, therefore it also depends only on the direction of the

momentum. This is completely similar to the stationary case where we were able

to make a transformation to the quasiclassical Green functions by performing an

integration of the corresponding equation over the energy variable d

Integrating now the nonstationary equation (8.60) over d

we find

(9.1)

end p.170

Top

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第5页共5页 2010-8-8 15:49

Here we introduce the quasiclassical collision integral

(9.2)

We again use the shortcut notation eqn (8.56) which now reads, for example,

(9.3)

Equation (9.2) was first obtained by Eliashberg (1971).

The integration over d

performed in eqn (9.2) for the coordinate

representation means, as in Section 5.1, that we take the limit

. Doing so we average out the coordinate dependence of the order parameter and

the vector potential over distances of order of

, i.e., over distances of the

atomic scale. In the momentum representation, the limit r

– r

0 implies that

we neglect terms of the first order in

, i.e., terms like

(9.4)

in the expansion of the convolution in powers of k/p

and keep only

zero–order terms like the simple product

. We shall discuss

this procedure in more detail later in Section 10.1. The same approximation was

used when we derived the Eilenberger equations for the stationary Green

functions. These terms can indeed be neglected in the Eilenberger equations for

the regular functions. However, they may sometimes become important in the

equations for the Keldysh functions. This is due to the fact that some leading

expansion terms vanish. We shall see later in Chapter 10 that one cannot neglect

the momentum derivatives for clean superconductors when the collision integrals

are small such that the mean free path

approaches . The

accuracy of eqn (9.2) becomes poor already for clean superconductors with

: some phenomena are lost in this description. The quasiclassical

equation (9.2) is thus applicable for superconductors if the mean free path of

quasiparticles is not very long. The limit of clean superconductors is discussed in

more detail in Section 10.2.

The corresponding equation for the anomalous function can be obtained from eqn

(8.55) in exactly the same way:

Kopnin, Nikolai, Senior Scientist, Low Temperature Laboratory, Helsinki University of

Technology, and L.D. Landau Institute for Theoretical Physics, Moscow

Theory of Nonequilibrium Superconductivity

Print ISBN 9780198507888, 2001

pp. [171]-[175]

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第1页共7页 2010-8-8 15:50

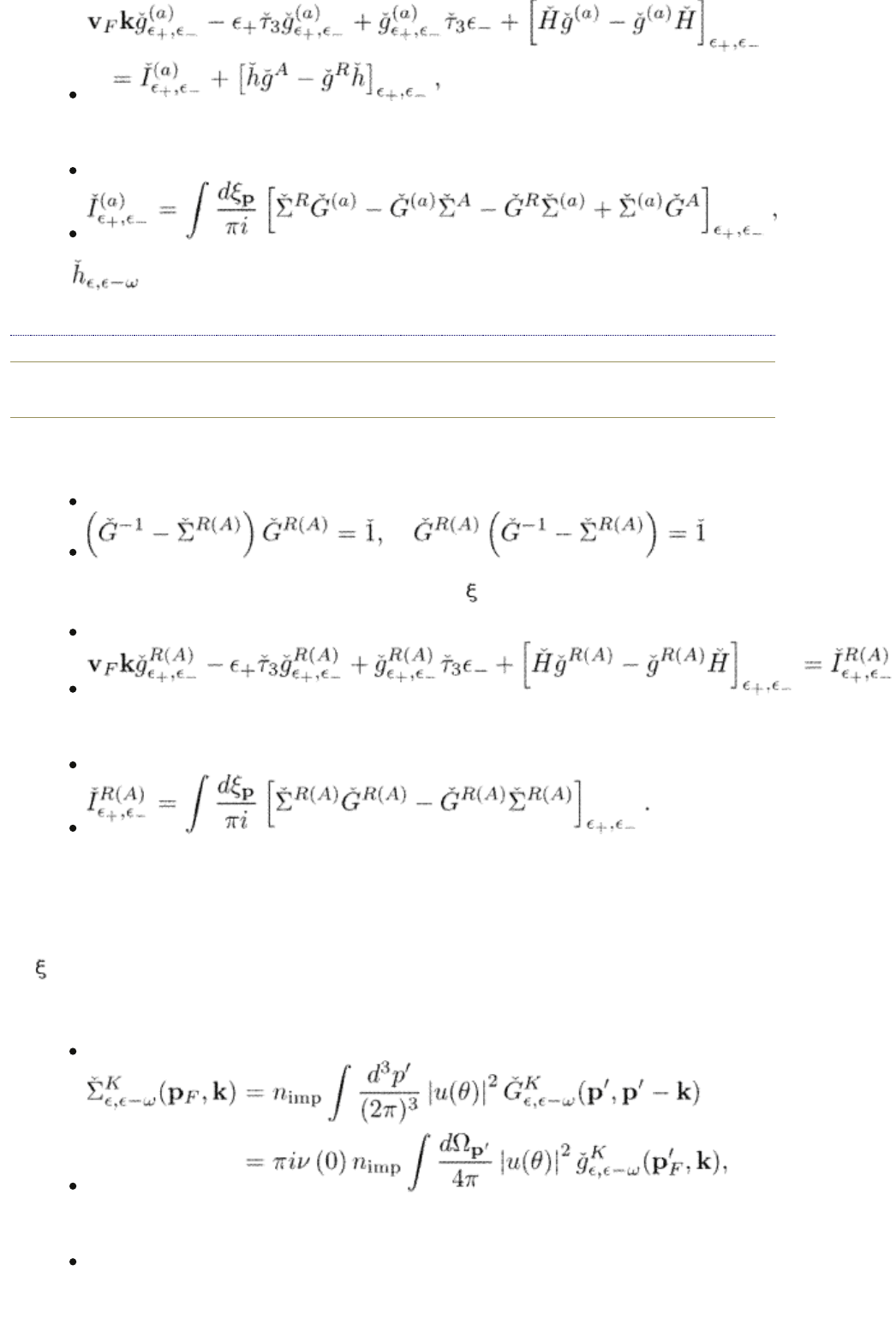
where

(9.5)

and are defined by eqn (8.10) on page 148.

end p.171

Of course, one can also obtain similar equations for the regular functions, as

well. Subtracting the left-handed and right-handed equations

(9.6)

from each other, and integrating the result over d

, we obtain

(9.7)

where the corresponding collision integral is

(9.8)

9.1.1 Self-energies

The self-energies in eqns (9.2), (9.5), and (9.8) also contain only the

-integrated Green functions; they depend only on the direction of the

momentum whose magnitude is fixed by the Fermi surface. Indeed, for

interaction with nonmagnetic impurities, we have

(9.9)

and

(9.10)

PRINTED FROM OXFORD SCHOLARSHIP ONLINE (www.oxfordscholarship.com)

Oxford Scholarship Online: Theory of Nonequilibrium Supe... http://www.oxfordscholarship.com/oso/private/content/phy...

第2页共7页 2010-8-8 15:50