Корзова Л.Н. Эконометрика
Подождите немного. Документ загружается.

Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
ГОУ ВПО «Дальневосточный государственный
университет путей сообщения»
Кафедра «Бухгалтерский учет и аудит»
Л.Н. Корзова
ЭКОНОМЕТРИКА
Методические указания
для выполнения самостоятельной работы
студентов экономических специальностей
по теме «Временные ряды»
Хабаровск
Издательство ДВГУПС
2008

2
УДК 330.43+519.862(075.8)
ББК У.в631я73
К 666
Рецензент:
Кандидат экономических наук,
Доцент кафедры «Бухгалтерский учет и аудит»
Дальневосточного государственного университета путей сообщения
И.В. Блажко
Корзова, Л. Н.
К 666
Эконометрика: метод. указания / Л.Н. Корзова. – Хабаровск :
Изд-во ДВГУПС, 2008. – 32 с.
Методические указания соответствуют Государственному образова-
тельному стандарту специальности «Бухгалтерский учет, анализ и аудит»
и «Финансы и кредит».
Методические указания предусматривают выполнение самостоятель-
ного задания студентами 2-го курса экономических специальностей по
разделу Временные ряды. В методических указаниях изложены теорети-
ческие основы по разделу Временные ряды, с помощью которых студенты
должны выполнить самостоятельную работу.
Следует отметить, что изложение теоретических положений сопровож-
дается примерами по различным видам моделей Временных рядов, что
должно помочь студентам в усвоении материала и выполнении самостоя-
тельной работы.
В Методических указаниях заданы необходимые варианты на выполне-
ние самостоятельной работы.
Предназначены для студентов дневной формы обучения.
УДК 330.43+519.862(075.8)
ББК У.в631я73
ГОУ ВПО «Дальневосточный государственный
университет путей сообщения» (ДВГУПС), 2008
3
ВВЕДЕНИЕ
Методы прогнозирования деловой активности являются важным инст-
рументом в процессе принятия решения в областях экономики.
Способность составить надежный прогноз показателей, например, за-
трат на рабочую силу, спрос на товары, себестоимость продукции может
оказать помощь предприятиям в конкурентной борьбе.
Прогноз можно использовать при принятии тактических и стратегиче-
ских решений.
Прогноз можно осуществлять различными способами.
В предложенной работе показано, как можно осуществить прогнозиро-
вание с помощью моделей Временных рядов, т.е. на основе учета истори-
ческих данных и выработки решений, основывались на прошлых значениях.
Цель пособия:
– помочь студенту в умении выбрать модели Временного ряда;
– показать возможность анализа моделей Временного ряда;
– показать приемы прогнозирования по различным моделям Времен-
ных рядов.
4
1. ВРЕМЕННЫЕ РЯДЫ. ПОНЯТИЕ. СВОЙСТВА.
СТРУКТУРА МОДЕЛЕЙ ВРЕМЕННЫХ РЯДОВ
Определение. Временной ряд (ВР) есть последовательность наблю-
дений некоторого объекта, признака (неслучайной величины)
Y
в после-
довательные (равностоящие) моменты времени.
Отдельные наблюдения признака
Y
называются уровнями ВР и обо-
значаются
nntY
t
,,...,,, 21
=
– число уровней ВР.
Каждый уровень ВР формируется под воздействием большого числа
факторов, которые можно подразделить на группы (факторы):
– факторы, формирующие тенденцию ВР;
– факторы, формирующие сезонные и циклические колебания ряда;
– случайные факторы.
В общем случае при исследовании экономических ВР можно использо-
вать следующую структуру ВР:
E
C
S
T
Y
+
+
+
=
или
E
C
S
E
Y
⋅
⋅
⋅
=
,
где
T
– тренд, плавно меняющаяся компонента, описывающая чистое
влияние долговременных факторов, т. е. длительную («вековую») тенден-
цию изменения признака;
S
– сезонная компонента, отражающая повто-
ряемость экономического процесса в течение не очень длительного пе-
риода времени (года, квартала, месяца и т. д.);
C
– циклическая компо-
нента, отражающая повторяемость экономического процесса в течение
длительного периода времени;
E
– случайная компонента, отражающая
влияние случайных факторов.
Часто при исследовании структуры ВР компоненты
S
и
C
объединяют,
т.к. методы их исследований схожи и выбирается для исследований струк-
тура
ntESTY
t
t
t
t
...,, 21
=
+
+
=
(1)
или
ntESTY
t
t
t
t
...,, 21
=
⋅
⋅
=
(2)
где (1) – так называемая аддитивная модель; (2) – мультипликативная мо-
дель.
Выбор модели ВР осуществляется на основе анализа структуры сезон-
ных колебаний.

5
Если амплитуда сезонных колебаний примерно постоянна, выбирается
модель (1), если амплитуда сезонных колебаний возрастает или уменьша-
ется выбирается модель (2).
Основные этапы анализа и построения моделей ВР.
– графическое представление ВР;
– выравнивание уровней ВР методом скользящей средней;
– выделение и удаление неслучайных составляющих (тренда, сезонной
составляющей);
– исследование случайной составляющей (проверка адекватности мо-
дели);
– прогнозирование с помощью построенной модели.
Различают стационарные ВР и ряды динамики.
Стационарные ВР – те, для которых вероятностные свойства не меня-
ются во времени.
Ряды динамики – те, которые в структуре своей содержат лагирован-
ные переменные (т. е. переменные, влияние которых характеризуется не-
которым запаздыванием, например,
1
1
−
−
t
t
Y
ε
, и т. д.).
1.1. Выбор модели ВР. Анализ моделей ВР.
Автокорреляция уровней ВР
Наиболее распространенным методом анализа ВР выделяют корреля-
ционный анализ, модели авторегрессии и модели скользящей средней.
Определение. Корреляционная зависимость между соседними уров-
нями ВР называется автокорреляцией уровней ВР.
Величина ее находится с помощью линейного коэффициента корреля-
ции между уровнями исходного ВР и уровнями данного ряда, сдвинутого
на несколько шагов во времени
)
(
τ
r
=
2
11
22
11
2
111
)()()()(
)(
∑∑∑∑
∑∑∑
−
=
+
−
=
+
−
=
−
=
−
=
+
−
=
−
=
+
−−−−
⋅−−
τ
τ
τ
τ
ττ
τ
τ
τ
τ
τ
ττ
τ
n
t
t
n
t
t
n
t
t
n
t
t
n
t
t
n
t
t
n
t
tt
yynyyn
yyyyn
, (3)
Число периодов (
τ
) по которым рассчитывается коэффициент автокор-
реляции называется лагом.
Свойства коэффициента автокорреляции:
– коэффициент автокорреляции вычисляют по аналогии с линейным
коэффициентом корреляции и определяют линейную тесноту связи теку-
щего и предыдущих уровней ВР.
По высокому коэффициенту автокорреляции можно судить о наличии
во ВР линейной или близкой к линейной тенденции.
6
По близким к нулю коэффициентам автокорреляции можно предполагать о
наличии нелинейной тенденции или предполагать, что имеет место модель ав-
торегрессии или модель скользящих средних или другие виды моделей.
– по знаку коэффициента автокорреляции нельзя судить о возрастаю-
щей или убывающей тенденции.
Существуют ВР, описывающие процессы, протекающие в экономике,
которые имеют положительные коэффициенты автокорреляции, но имею-
щие убывающую тенденцию.
Определение. Последовательность коэффициентов автокорреляции
называют автокорреляционной функцией.
Замечание. Следует различать понятия коэффициента автокорреляции
и автокорреляционной функции.
Коэффициент автокорреляции определяется при значении фиксиро-
ванного лага, а автокорреляционная функция представляет зависимость
коэффициента автокорреляции от величины лага.
Анализ автокорреляционной функции позволяет выявить структуру ВР.
– если наиболее высоким оказался коэффициент автокорреляции пер-
вого порядка, исследуемый ряд содержит только тенденцию;
– если наибольшим оказался коэффициент автокорреляции порядка
τ
то ВР содержит циклические колебания с периодом
τ
;
– если коэффициенты автокорреляции малы, то либо ряд имеет нели-
нейную тенденцию и в качестве уравнения тренда исследовать нелиней-
ные модели, например,
ε++=
t
в
aY
t
,
ε++= tвaY
t
,
ε++=
t
в
aY
t
,
ε+++=
2
ctbtaY
t
,
ε+++=
3
ctbtaY
t
и т. д.
либо имеют место модели авторегрессии порядка p (autoregressive model)
tptpttt
YbYbYbaY
ε
+
+
+
+
+
=
−−−
...
2211
(4)
либо модели скользящих средних порядка q (moving average model)
qtqtttt
lllY
−−−
+
+
+
+
=
ε
ε
ε
ε
...
2211
(5)
либо другие модели.

7
1.2. Автокорреляция остатков ВР
Особенностью ВР является то, что остатки (
ε
) не всегда являются не-
зависимыми, т. е. условие
ji
r
εε
= 0, i ≠ j, не выполняется, что постулирует-
ся для регрессионных моделей.
Такие модели называются моделями с наличием автокорреляции ос-
татков.
Одной из причин автокорреляции ошибок является наличие «скрытых»
регрессоров, влияние которых проявляется через случайную величину
ε
.
Выявление этих составляющих иногда позволяет получить модель без
автокорреляции остатков ряда.
Другой причиной может быть влияние на результативный признак ве-
личин
qttt −−−
ε
ε
ε
,...,,
21
.
Возможным приемом устранения автокорреляции остатков является
подбор и построение моделей или (4) или (5) или их комбинацию или дру-
гие модели.
Замечание. Проверить наличие автокорреляции остатков можно тра-
диционным способом, а также с помощью известных критериев (тестов).
Одним из них является тест Дарбина-Уотсона.
Согласно теста находят величину
d =
∑
∑
=
=
−
−
n
t
t
n
t
tt
1
2
2
2
1
ε
εε )(
,
где n – объем выборки.
Если:
а) d
B
< d < 4-d
B
, гипотеза об отсутствии автокорреляции принимается;
б) d
H
< d < d
B
или 4-d
B
< d < 4-d
H
определенного ответа тест не дает (об-
ласть неопределенности теста);
в) 0 < d < d
H
, принимается гипотеза о наличии положительной автокор-
реляции;
г) 4-d
H
< d < 4, принимается гипотеза об отрицательной автокорреля-
ции.
Границы d
H
и d
B
при уровне значимости d = 0,05 показаны в прил. 1.

8
2. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. В чем существенное отличие модели ВР от регрессионной модели?
2. Принцип выбора модели ВР.
3. Суть процедуры сглаживания ВР.
4. Суть коэффициента корреляции между уровнями ВР.
5. Причины автокорреляции остатков ВР.
6. Способы выявления автокорреляции остатков.
7. Отличие стационарных и динамических ВР.
8. Принципы выбора моделей тренда.
3. ПРИМЕРЫ ПОСТРОЕНИЯ МОДЕЛЕЙ ВРЕМЕННЫХ РЯДОВ
Пример 1
Пусть известны объемы потребления продукта А (
t
Y) за 15 недель
осенне-зимнего периода по району Ц города Х.
Таблица 1
t
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
t
Y
3,38
3,53
3,7
3,8
3,78
3,84
3,76
3,9
4,15
4,28
4,4 4,54
4,78
4,84
4,88
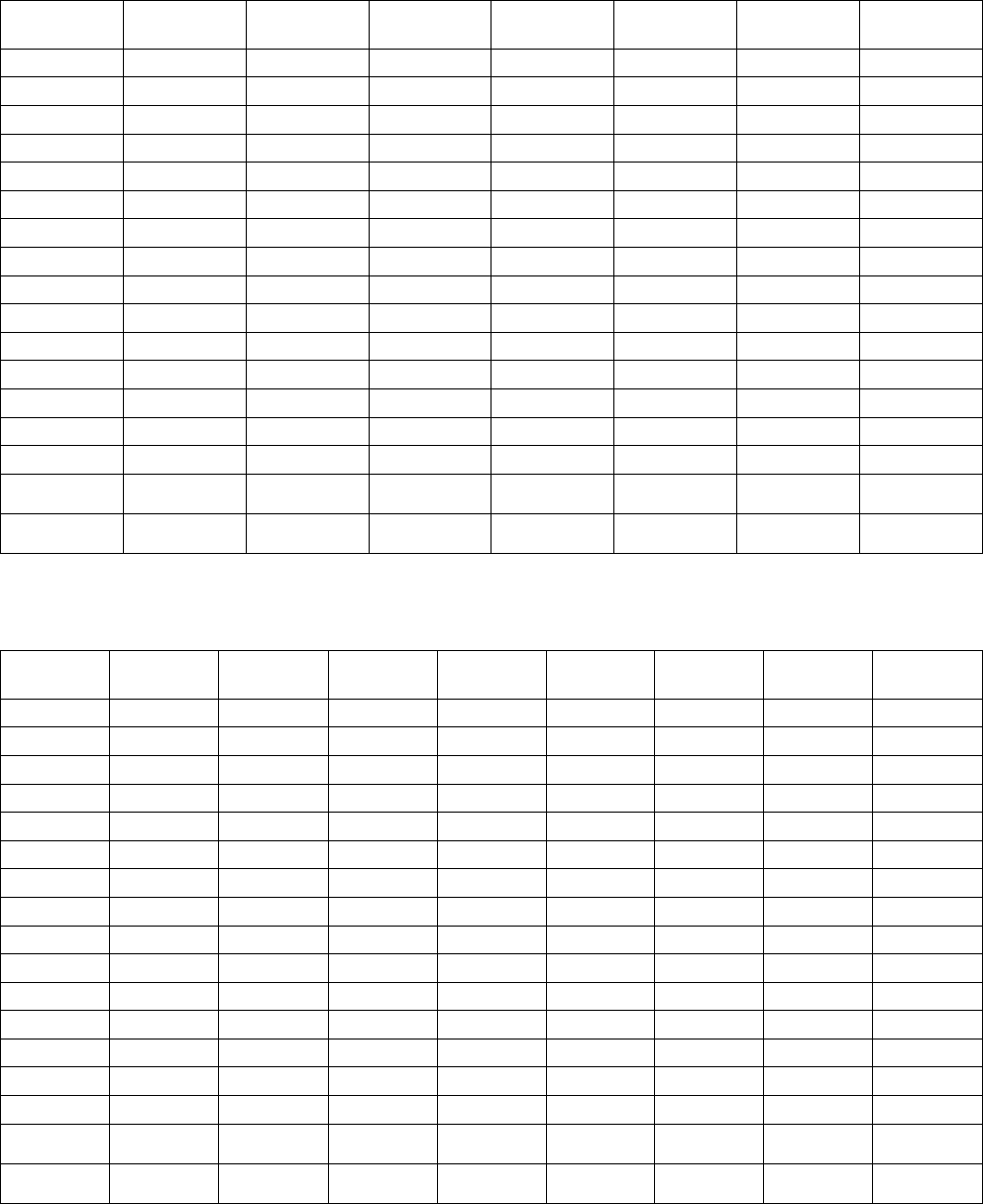
Задание: используя значения, полученные в табл. 2, выявить структуру
ряда, выбрать модель и оценить ее.
Таблица 2
t Y
t
Y
t
Y
t+1
Y
t
Y
t+1
2
t
Y
2
1
+
t
Y
t²
1
3,380
3,380
3,530
11,931
11,424
12,461
1
2
3,530
3,530
3,700
13,061
12,461
13,690
4
3
3,700
3,700
3,800
14,060
13,690
14,440
9
4
3,800
3,800
3,780
14,364
14,440
14,288
16
5
3,780
3,780
3,840
14,515
14,288
14,746
25
6
3,840
3,840
3,760
14,438
14,746
14,138
36
7
3,760
3,760
3,900
14,664
14,13
8
15,210
49
8
3,900
3,900
4,150
16,185
15,210
17,223
64
9
4,150
4,150
4,280
17,762
17,223
18,318
81
10
4,280
4,280
4,400
18,832
18,318
19,360
100
11
4,400
4,400
4,540
19,976
19,360
20,612
121
12
4,540
4,540
4,780
21,701
20,612
22,848
144
13
4,780
4,7
80
4,840
23,135
22,848
23,426
169
14
4,840
4,840
4,880
23,619
23,426
23,814
196
15
4,880
—
—
—
—
—
225
∑
61,560
56,680 58,180 238,245 232,183 244,573 1240
∑
/n
4,104
82,667
9
Продолжение табл.2
t Y
t
Y
t+2
Y
t
Y
t+2
2
t
Y
2
2
+
t
Y
tY
t
2
t
Y
1
3,380
3,700
12,506
11,424
13,690
3,380
11,424
2
3,530
3,800
13,414
12,461
14,440
7,060
12,461
3
3,700
3,780
13,986
13,690
14,288
11,100
13,690
4
3,800
3,840
14,592
14,440
14,746
15,200
14,440
5
3,780
3,760
14,213
14,288
14,138
18,900
14,288
6
3,840
3,900
14,976
14,746
15,210
23,040
14,746
7
3,760
4,150
15,604
14,138
17,223
26,320
14,138
8
3,900
4,280
16,692
15,210
18,318
31,200
15,210
9
4,150
4,400
18,260
17,223
19,360
37,350
17,223
10
4,280
4,540
19,431
18,318
20,612
42,800
18,318
11
4,400
4,780
21,032
19,360
22,848
48,400
19,360
12
4,540
4,840
21,974
20,612
23,426
54,480
20,612
13
4,780
4,880
23,326
22,848
23,814
62,140
22,848
14
— —
—
— — 67,760
23,426
15
— —
—
— — 73,200
23,814
∑
51,840
54,650
220,006
208,758
232,113
522,330
255,998
∑
/n
34,822
17,067
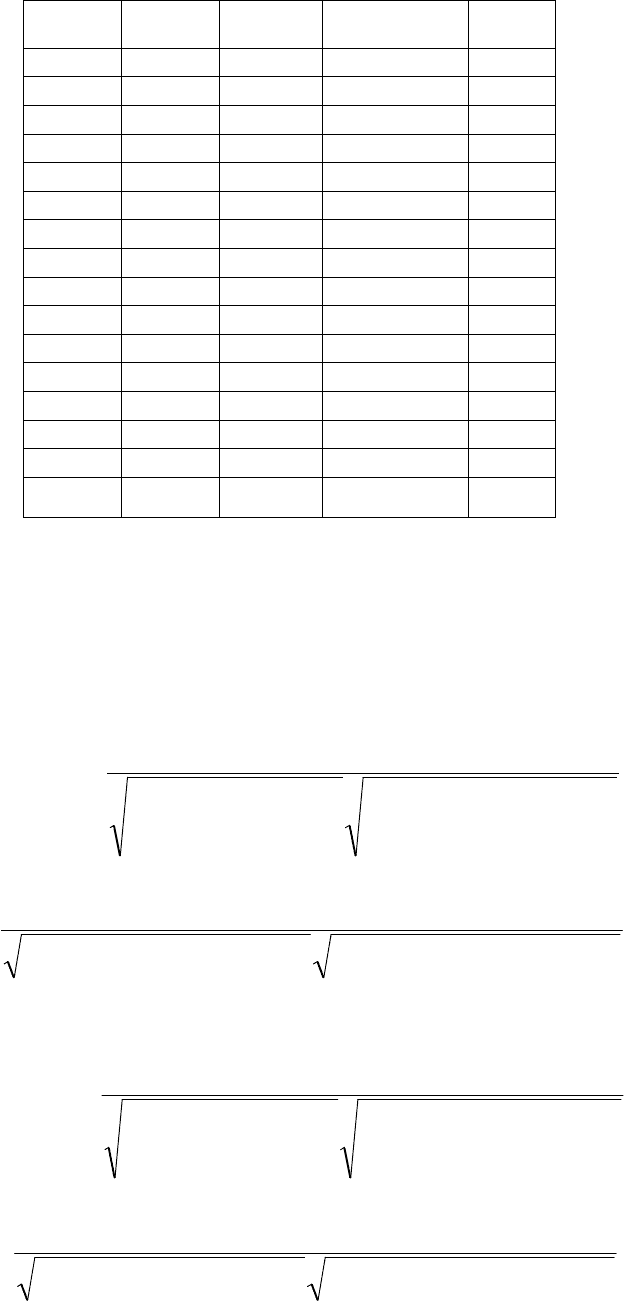
Продолжение табл.2
t Y
t
Y
t+3
Y
t
Y
t+3
2
t
Y
2
3
+
t
Y
t Ŷ
ε
1
3,380
3,800
12,844
11,424
14,440
1
3,355
0,025
2
3,530
3,780
13,343
12,461
14,288
2
3,462
0,068
3
3,700
3,840
14,208
13,690
14,746
3
3,569
0,131
4
3,800
3,760
14,288
14,440
14,138
4
3,676
0,124
5
3,780
3,900
14,742
14,288
15,210
5
3,783
-0,003
6
3,840
4,150
15,936
14,746
17,223
6
3,890
-0,050
7
3,760
4,280
16,093
14,138
18,318
7
3,997
-0,237
8
3,900
4,400
17,160
15,210
19,360
8
4,104
-0,204
9
4,150
4,540
18,841
17,223
20,612
9
4,211
-0,061
10
4,280
4,780
20,458
18,318
22,848
10
4,318
-0,038
11
4,400
4,840
21,296
19,360
23,426
11
4,425
-0,025
12
4,540
4,880
22,155
20,612
23,814
12
4,532
0,008
13
— — — — — 13
4,639
0,141
14
— — — — — 14
4,746
0,094
15
— — — — — 15
4,853
0,027
∑
47,060
50,950
201,365
185,909
218,423
120,000
0,000
∑
/n
8,000
0,000
10
Окончание табл.2
t
t
ε
1
−
t
ε
(
t
ε
-
1
−
t
ε
)
2
2
t
ε
1
− − − 0,001
2
0,068
0,025
0,002
0,005
3
0,131
0,068
0,004
0,017
4
0,124
0,131
0,000
0,015
5
-0,003
0,124
0,016
0,000
6
-0,050
-0,003
0,002
0,003
7
-0,237
-0,050
0,035
0,056
8
-0,204
-0,237
0,001
0,042
9
-0,061
-0,204
0,020
0,004
10
-0,038
-0,061
0,001
0,001
11
-0,025
-0,038
0,000
0,001
12
0,008
-0,025
0,001
0,000
13
0,141
0,008
0,018
0,020
14
0,094
0,141
0,002
0,009
15
0,027
0,094
0,004
0,001
∑
0,107
0,173
Решение.
Рассчитаем коэффициенты автокорреляции первого, второго, третьего
порядков, используя формулу (3).
Значения для расчетов берем из табл. 2.
r(τ = 1) =
2
14
1
1
14
1
2
1
2
14
1
14
1
2
14
1
1
14
1
14
1
1
1414
14
)()(
∑∑∑∑
∑∑∑
=
+
=
+
==
=
+
==
+
−−
⋅−
t
t
t
t
t
t
t
t
t
t
t
t
t
tt
yyyy
yyyy
;
r(τ = 1) =
22
185857324414685618323214
1858685624523814
),(,),(,
,,,
−⋅−⋅
⋅
−
⋅
= 0,981;
r(τ = 2) =
2
13
1
2
13
1
2
2
2
13
1
13
1
2
13
1
2
13
1
13
1
2
1313
13
)()(
∑∑∑∑
∑∑∑
=
+
=
+
==
=
+
==
+
−−
⋅−
t
t
t
t
t
t
t
t
t
t
t
t
t
tt
yyyy
yyyy
;
r(τ = 2) =
22
65541132321384517520813
6554845100622013
),(,),(,
,,,
−⋅−⋅
⋅
−
⋅
= 0,899;
