Лабоцкий В.В. Управление знаниями
Подождите немного. Документ загружается.

31
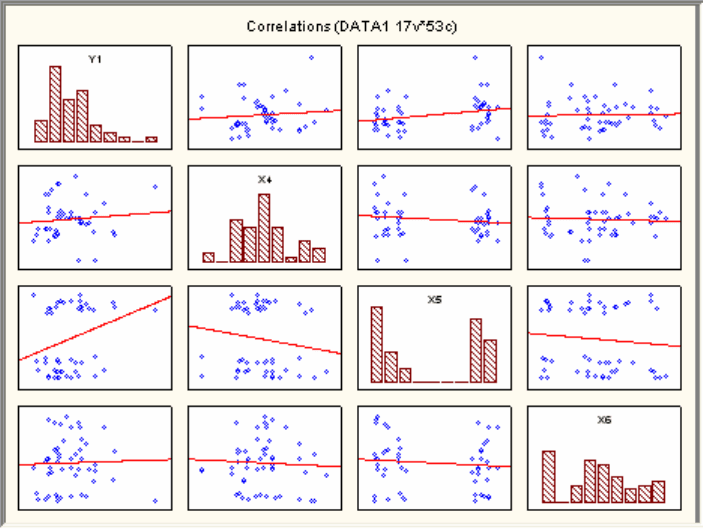
Рис. 2.12
2.3. СОЗДАНИЕ ОТЧЕТА
Результаты анализа в STATISTICA представляются тремя способами:
в окне, рабочей книге (
Workbook) и отчете (Report).
В
STATISTICA каждый анализ выводится в своем собственном окне
в рабочей области системы. Как только это окно становится активным,
изменяются панель инструментов и меню. В нем появляются команды и
инструменты, доступные для этого типа документов.
Рабочая книга является промежуточным (рабочим) вариантом
хранения результатов. Имеется единственный формат этих файлов *.
stw.
Отчет – это документ системы
STATISTICA (по умолчанию файл в
формате
*.str), в котором может сохраняться любая текстовая, числовая и
графическая информация. Отчет необходим для окончательного
представления результатов анализа и вывода их на печать. Кроме того,
отчеты могут сохраняться в следующих форматах:
*.rtf - это удобный способ подготовки отчета о проделанной работе.
Позволяет выводить в него как текстовую, числовую, так и графическую
информацию. Вы можете отредактировать этот отчет либо в
STATISTICA,
либо загрузив его в какой-либо текстовой редактор, например, MS Word
for Windows;
*.
txt - при выборе этой опции содержимое электронных таблиц будет
выводиться в текстовой файл, с потерей графической информации;
*.
htm – вывод результатов происходит в Web-документы.
32
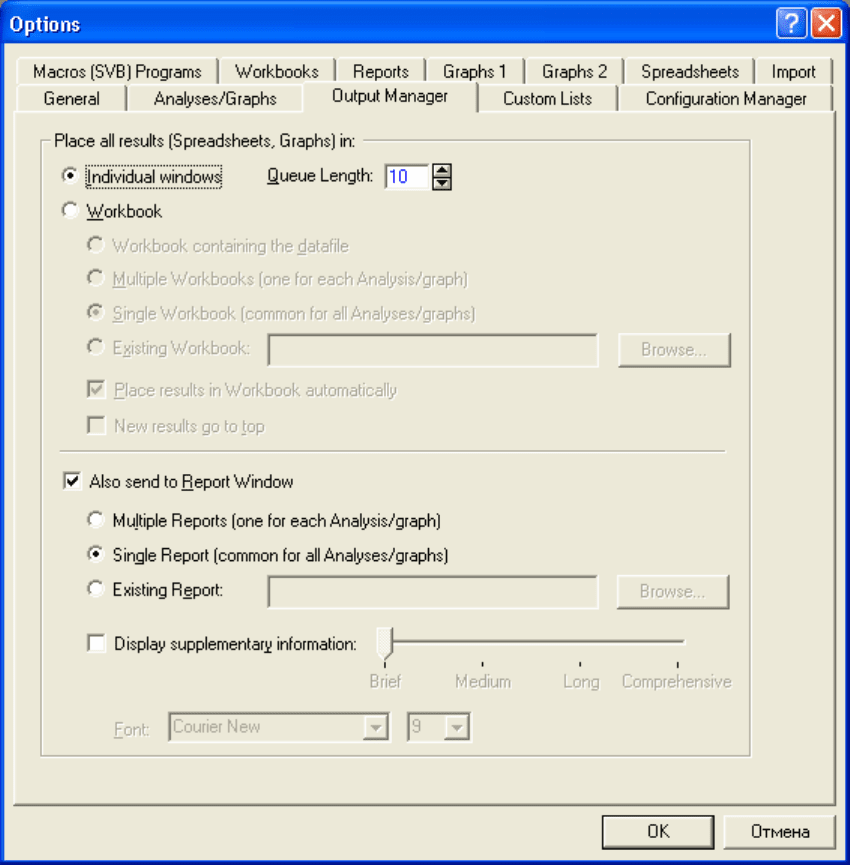
Не вдаваясь в подробности настроек рабочих книг и отчетов, для
выполнения этих и последующих индивидуальных заданий, целесообразно
использовать только единственный отчет для автоматического вывода всех
результатов анализа. Соответствующие установки можно сделать, как
показано на панели (Рис. 2.13), вызываемой по команде
Tools/Options, в
закладке OutputManager.
Примечание: Файл с исходными данными в данный отчет
автоматически не помещается.
Рис. 2.13
33
3. РЕГРЕССИОННЫЙ АНАЛИЗ
Все модели неправильны,
но некоторые полезны.
Джордж Бокс
3.1. ОБЩИЕ СВЕДЕНИЯ. ПРОСТАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
3.1.1. Функция регрессии
Понятия регрессии и корреляции непосредственно связаны между
собой, но при этом существует различие между ними. В корреляционном
анализе оценивается сила стохастической связи, а в регрессионном анализе
исследуются формы.
В регрессионном анализе изучается связь и определяется
количественная зависимость между зависимой переменной и одной или
несколькими независимыми переменными, рассматриваемые как
неслучайные величины. Пусть
переменная Y зависит от одной переменной
x
. При этом предполагается, что переменная
x
принимает заданные
фиксированные значения, а зависимая переменна Y имеет случайный
разброс из-за ошибок измерения, влияния неучтенных факторов и т.д.
Каждому значению
x
соответствует некоторый закон распределения
вероятностей случайной величины Y. Предположим, что Y в "среднем"
линейно зависит от значений переменной
x
. Это означает, что условное
математическое ожидание случайной величины Y при заданном значении
x
имеет вид
xaaxYM
10
)/(
+
=
.
Данная функция называется линейной теоретической функцией
регрессии Y на
x
, а параметры
0
a
и
1
a
– параметрами линейной
регрессии (коэффициенты регрессии). На практике параметры регрессии
определяются по результатам наблюдений переменных Y
и
x
, связь
между которыми можно записать
ε
+
+
=
хaaY
10
,
где
ε
– случайная ошибка наблюдений.
3.2. ПОСЛЕДОВАТЕЛЬНОСТЬ РЕГРЕССИОННОГО АНАЛИЗА
• Формулировка задачи.
•
Идентификация переменных (определение входных и выходных
переменных).
•
Сбор статистических данных.
•
Спецификация функции регрессии (определение вида модели).

34
•
Оценивание параметров функции регрессии.
•
Оценка точности регрессионного анализа:
1)
Проверка адекватности всей модели, т.е. согласуются ли
предсказанные значения выходной величины с наблюдаемыми данными;
2)
Проверка значимости параметров модели, т.е. значимо ли они
отличаются от нуля или нет.
•
Интерполяция результатов, анализ, оптимизация и
прогнозирование.
Предпосылки к проведению регрессионного анализа
• Случайные ошибки наблюдений имеют нормальный закон
распределения
.)( 0,)( , ),0(
2
constDMN ===→
σεεσε
•
Отсутствие автокорреляции между ошибками наблюдений, т.е.
последовательные значения
ε
i
не зависят друг от друга.
Метод наименьших квадратов
Для нахождения оценок параметров модели по результатам
наблюдений используется метод наименьших квадратов (МНК). Пусть
проведено n независимых наблюдений случайной величины Y
при
соответствующих значениях
x
, совместный закон распределения которых
неизвестен. Следовательно, теоретическую функцию регрессии мы не
сможем найти. Наша задача оценить эмпирическую функцию регрессии
.
~
~
~
10
xaay
+
=
Согласно МНК, параметры подбираются таким образом, чтобы
минимизировать сумму квадратов отклонений наблюдаемых значений от
расчетных по модели значений
min,)
~~
()
~
(
2
10
1
2
11
2
→−−
∑
=−
∑
=
∑
=
===
i
n
i
ii
n
i
i
n
i
i
x
aa
yyy
eF
где
y
i
– наблюдаемые значения выходной переменной;
y
i
~
–
значения выходной переменной, рассчитанные по модели.
Из необходимых условий минимума
⎪
⎪
⎩
⎪
⎪
⎨
⎧
∑
=−−−=
∑
=−−−=
=
=
n
i
i
i
n
i
i
x
)x
aa
y
i
(
a
F
)x
aa
y
i
(
a
F
1
10
1
1
10
0
0
~~
2
~
,0
~~
2
~
∂
∂
∂
∂
находим оценки параметров
a
0
и
a
1
(здесь и далее, если это не мешает
пониманию, знак ~ над параметрами будет опускаться). Они будут
определяться из решения системы двух линейных уравнений

35
⎩
⎨
⎧
∑∑
=+
∑
∑∑
=+
.
,
2
10
10
x
y
xaxa
y
xaa
n
i
i
ii
i
i
Здесь и далее, если это не оговорено особо, суммирование
происходит от i=1,n,(1). Оценки параметров, получаемые по методу МНК,
при условии выполнения предпосылок относительно случайных ошибок
наблюдений, будут обладать следующими свойствами:
•
несмещенность;
•
состоятельность;
•
эффективность.
Проверка адекватности модели
Для проверки гипотезы адекватности модели необходимо сравнить
две суммы квадратов:
1)
Остаточную сумму квадратов, характеризующую отклонение от
регрессии
.)
~
(
2
11
2
yy
e
Q
i
n
i
i
n
i
i
e
−
∑
=
∑
=
==
2)
Сумму квадратов, обусловленную регрессией
,
)
~
(
2
1
y
yQ
n
i
iR
−
∑
=
=
где
∑
=
=
n
i
i
y
n
y
1
1
.
Тогда выборочное значение
F, имеющее распределение
Фишера
,
)1/(
/
−−
=
kn
Q
k
Q
F
e
R
может служить проверкой адекватности для заданного уровня значимости
λ (обычно для экономических задач λ=0,05) и степеней свободы
f
1
=
k
;
f
2
=
1−− kn
, где
k
– число оцениваемых параметров, исключая
свободный коэффициент.
Если F ≥
F
λ; f1; f2
– модель адекватна (прил.1). Остаточную
дисперсию ошибки
)1/(
2
−−= kn
Q
S
e
36
можно использовать в качестве оценки дисперсии
σ
2
– дисперсии
случайной величины. Результаты проверки адекватности удобно
представить в виде (табл. 3.1).
Полезной характеристикой линейной регрессии является
коэффициент детерминации, вычисляемый по формуле
.1
2
QQ
Q
QQ
Q
R
eR
e
eR
R
+
−=
+
=
Таблица 3.1
Источник
изменения
Сумма квадратов
Число
степеней
свободы
Оценка
дисперсии
Модель
2
1
)
~
(
y
yQ
n
i
iR
−
∑
=
=
k
k
Q
S
R
R
/
2
=
Ошибка
2
1
1
2
)
~
(
yy
e
Q
i
n
i
i
n
i
i
e
−
∑
=
∑
=
=
=
1
−
−
kn
)1/(
2
−
−
= kn
Q
S
e
Сумма
2
1
)
(
y
yQQ
n
i
iRe
−
∑
=+
=
1
−
n
Коэффициент детерминации равен той доле результатов наблюдений
относительно горизонтальной прямой
yy
=
, которая объясняется
уравнением регрессии. Величина
R
R
2
+=
является оценкой
множественного коэффициента корреляции между результатами
наблюдений и вычисленными значениями
y
i
~
. Если R
2
=0.75 это значит,
что модель работает на 75%, а 25% приходится на ошибку или неучтенные
в модели факторы (для практических целей целесообразно, чтобы R
2
≥
0,75). Для небольших значений n<30 необходимо использовать
скорректированный коэффициент детерминации
).1(
1
1
1
22*
R
kn
n
R
−
−−
−
−=
Проверка значимости параметров модели
В результате проверки устанавливается статистическая значимость
или незначимость отличия от нуля оценок параметров регрессии. Это
проверка осуществляется отдельно для каждого параметра модели. Для
37
оценки значимости коэффициентов регрессии можно воспользоваться
следующим правилом, если абсолютная величина коэффициента регрессии
больше доверительного интервала, то гипотеза о незначимости
коэффициента отвергается:
StaaSta
a
i
f
ii
a
i
f
i
2/ ,2/ ,
~
~
λλ
+
<
<
−
,
Sta
a
i
fi
~
2/ ,
λ
≥
,
где
t
f 2/,
λ
– значение Стьюдента, определяемое по числу степеней
свободы
f=
1−− kn
и λ=0,05 (прил.2);
s
a
i
– редние квадратические
отклонения (с.к.о.) ошибок коэффициентов регрессии, для простой
линейной регрессии
xaay
10
+
=
они могут быть вычислены
соответственно
,
)(
2
2
22
0
∑∑
−
∑
=
x
x
n
xS
S
a
.
)(
2
2
1
∑∑
−
=
2
x
x
n
S
n
S
a
Можно проверять значимость коэффициентов по
t-критерию.
Воспользуемся формулой
.
~
S
a
t
a
i
i
=
Вычисленное значение сравнивается с табличным и если
t ≥ t
f; λ/2,
то
коэффициент значим. В противном случае соответствующую переменную
можно исключить из модели и все расчеты, включая решение системы
линейных уравнений, повторить снова.
3.3. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ
Множественная линейная регрессия представляет собой выражение
....
~
22110 kk
xaxaxaay
+
+
+
+
=
Для случая
k
=2 по результатам наблюдений система нормальных
уравнений, полученная МНК, будет иметь вид
⎪
⎩
⎪
⎨
⎧
∑
=
∑
+
∑
+
∑
∑
=
∑
+
∑
+
∑
∑
=
∑
+
∑
+
. 22212
, 12111
, 21
2
210
2
2
10
210
iiiiii
iiiiii
iii
xyxaxxaxa
xyxxaxaxa
yxaxana
Дальнейшие рассуждения удобно вести, используя следующие
матричные обозначения:
38
, наблюдений вектор -
.
.
2
1
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
y
y
y
Y
k
, параметров вектор -
.
.
1
0
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎜
⎜
⎜
⎝
⎛
=
a
a
a
a
k
1)k (n -
1
....
..
..
...
1
...
1
матрица ная регрессион
21
2
22
12
1
21
11
+=
⎟
⎟
⎟
⎠
⎞
⎜
⎜
⎜
⎝
⎛
xxx
xxx
xx
A
knnn
k
x
k
.
Система нормальных уравнений имеет вид
YAaAA
TT
=)(
. При
условии, что
A
A
T
– невырожденная матрица, решение системы можно
записать в виде
.)(
1
YAAAa
TT −
=
Ковариационная матрица оценок параметров регрессионной модели
будет равна
.)(
1
2
−
= AA
S
K
T
a
j
a
i
Дисперсии параметров модели определяются соотношением
.
2
K
S
a
i
a
i
a
i
=
Во множественной линейной регрессии предпосылки регрессионного
анализа и его проведение полностью совпадают с простой линейной
регрессией. Особенностью множественной регрессии является корреляция
независимых переменных. Желательно избегать включения в модель
линейно зависимых переменных.
3.4. НЕЛИНЕЙНЫЕ МОДЕЛИ, СВОДЯЩИЕСЯ К ЛИНЕЙНЫМ
Существуют два вида нелинейности регрессионных моделей:
Нелинейные относительно независимых переменных.
Например,
xxaxaxaa
y
213
2
22110
~
+++=
.
В этом случае необходимо просто сделать замену переменных:
.
~
,
,
2
3
1
2 11 0
2
2 1
1
2
2
z
a
z
axaa
y
z
xx
z
x
+++=
==
Нелинейные относительно параметров регрессии.

39
Например,
.
1
~
10
x
aa
y
+
=
Выполним функциональное преобразование:
,
~
1
пусть
y
z =
.
10
тогда xaaz
+
=
К сожалению, не всегда можно функциональными преобразованиями
от нелинейных моделей перейти к линейным. Кроме того, нужно иметь в
виду, что при вычислении параметров по методу МНК минимизируется
сумма квадратов отклонений преобразованных, а не исходных данных.
3.5. ПРОВЕРКА ПРЕДПОСЫЛОК РЕГРЕССИОННОГО АНАЛИЗА
3.5.1. Проверка нормальности закона распределения ошибок
Анализ ошибок проводится по следующей схеме. Предполагаем, что
),0(~
σ
ε
N
i
, тогда
)1,0(~ N
i
ε
. Тогда, если модель правильна, то
дисперсия остатков, характеризующая качество аппроксимации
результатов наблюдений
,
11
)(
1
1
2
2
1
2
−−
∑
=
−−
∑
−
=
−−
=
==
kn
e
kn
e
e
kn
Q
S
n
i
i
n
i
i
e
служит оценкой величины
σ
2
– дисперсии ошибок наблюдений, где
−e
среднее значение отклонений. Случайная величина
Se
i
/
представляет
собой единичные нормальные отклонения. Если эти отклонения будут
находиться в интервале [-2; 2] , то, следовательно, наше предположение о
том, что
),0(~
σ
ε
N
i
не ошибочно.
3.5.2. Проверка на однородность случайных ошибок
Для проверки на однородность дисперсии D(ε)=const. Целесообразно
воспользоваться методом Гольфельда. Последовательность значений
случайной величины Y
разбивается на две последовательности объемом n
1
и n
2
, где (n
1
+n
2
=n). Для каждой последовательности вычисляются
дисперсии воспроизводимости
S
2
1
и
S
2
2
. Тогда отношение
S
S
F
2
1
2
2
=
,

40
при
S
2
1
<
S
2
2
будет иметь распределение Фишера со степенями свободы
f
1
=
1
1
−− kn
; f
2
=
1
2
−− kn
. Если значение F превышает табличное, то
гипотеза об однородности дисперсии отклоняется. Чувствительность
критерия увеличивается, если исключить средние наблюдения.
В случае, если дисперсии оказались неоднородными, часто
оказывается полезным изменение масштаба для выходной переменной.
Вводится некоторая функция от выходной переменной, например
yln
или
y.
3.5.3. Проверка на автокорреляцию случайных ошибок
Наличие автокорреляции ошибок можно проверить с помощью
критерия Дарбина-Уотсона:
.
)(
1
2
2
2
1
∑
∑
−
=
=
=
−
n
i
i
n
i
ii
e
ee
DW
Критерий Дарбина-Уотсона изменяется в диапазоне 0 ≤ DW ≤ 4. При
отсутствии автокорреляции DW=2. В приложении 3 приводятся нижние и
верхние границы критерия dн и dв
для степеней свободы f
1
=n; f
2
=k.
Если
0 ≤ DW ≤ dн,
есть положительная автокорреляция,
4–dн
≤ DW ≤ 4, есть отрицательная автокорреляция,
dв
≤ DW ≤ 4–dв,
автокорреляция отсутствует,
dн
< DW < dв или 4–dв ≤ DW ≤ 4–dн, нужны дополнительные
исследования.
П р а к т и ч е с к и й с о в е т: желательно область
неопределенности подключить к области отклонения гипотезы об
отсутствии автокорреляции.
3.6. ОПИСАНИЕ ТИПОВОГО ПРИМЕРА
В табл. 3.2 приведены значения выходной переменной
y
i
при
данном значении входной переменной
x
i
. Модель ищется в виде
xa
a
y
1
0
~
+
=
.
Таблица 3.2
X 1 2 3 4
Y 2 4 5 7
