Лабоцкий В.В. Управление знаниями
Подождите немного. Документ загружается.


41
1.
Вычислим оценки математических ожиданий, смещенные и
несмещенные оценки дисперсий и средних квадратических отклонений:
∑∑
==== 5,4
1
, 5,2
1
y
n
y
x
n
x
i
i
,
,251,3)(
1
, 250,1)(
1
2222
=−==−=
∑∑
yy
n
Sxx
n
S
iyiх
, 333,4)(
1
1
, 666,1)(
1
1
2222
=−
−
==−
−
=
∑∑
yy
n
Sxx
n
S
iyнiхн
, 803,1)(
1
, 118,1)(
1
22
=−==−=
∑∑
yy
n
Sxx
n
S
iyiх
. 082,2)(
1
1
, 291,1)(
1
1
22
=−
−
==−
−
=
∑∑
yy
n
Sxx
n
S
iyнiхн
2.
Определим модель. Вычислим соответствующие суммы и
составим систему двух линейных уравнений:
Σx
i
=10, Σy
i
=18, Σx
i
2
=30, Σx
i
y
i
=53, Σy
i
2
=94,
⎪
⎩
⎪
⎨
⎧
=+
=+
, 533010
, 1810 4
10
10
aa
aa
решая которую, получаем:
a
0
= 0,5,
a
1
=1,6. Модель имеет вид
xy 6,15,0
~
+
=
3. Рассчитаем модельные значения, подставляя в уравнение значения
входной переменной (табл. 3.3).
Таблица 3.3
y
~
2,1 3,7 5,3 6,9
4. Определим адекватность модели, для этого вычислим общую
сумму квадратов, сумму квадратов, относящуюся к регрессии, и сумму
квадратов остатков:
13
4
)18(
94
)(
)(
22
2
2
=−=
∑
−
∑
=
∑
−=
n
y
y
yyQ
i
;
=−
∑
=
2
)
~
( y
yQ
iR
; 8,12
4
)18(
8,93
)(
~
22
2
=−=
∑
−
∑
n
y
y
Q
e
=Σe
i
2
=(2–2,1)
2
+(4–3,7)
2
+(5–5,3)
2
+(7–6,9)
2
=0,2 .
42
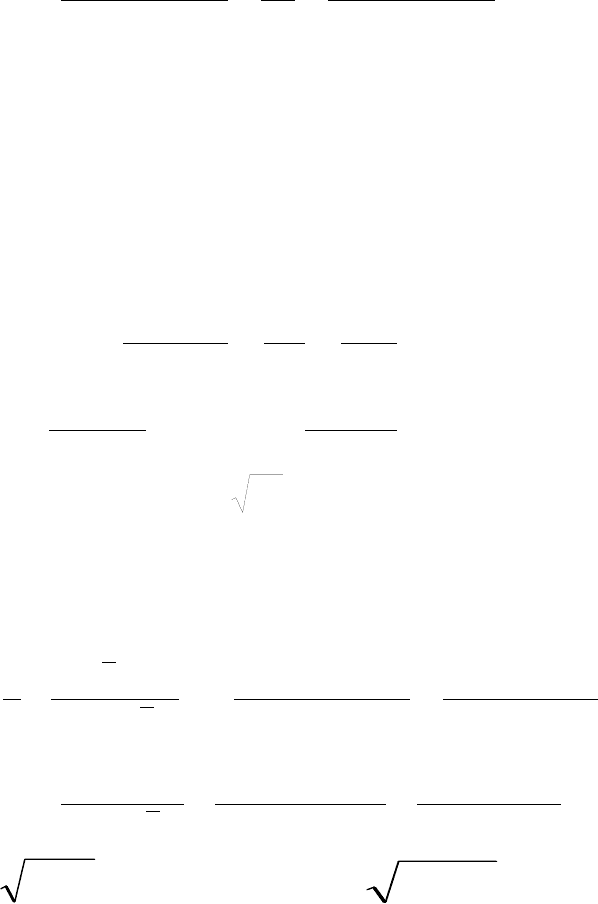
Для проверки полученных расчетов необходимо, чтобы
.
eR
QQQ +=
В нашем случае равенство выполняется.
Расчетное значение критерия Фишера равно
.128
)114/(2,0
1/8,12
)1/(
/
2
2
=
−−
==
−−
=
S
S
kn
Q
k
Q
F
R
e
R
Расчетное значение критерия Фишера больше, чем табличное
значение F > F
ТАБЛ.
=F
0,05;1;2
=18,512.
Вывод 1: модель адекватна, исходные данные хорошо согласуются с
модельными данными.
5.
Оперативно адекватность модели можно проверить по
коэффициентам детерминации или корреляции. Коэффициент
детерминации, скорректированный коэффициент детерминации и
коэффициент корреляции определяются следующим образом:
,9846,0
13
8,12
2
===
+
=
Q
Q
QQ
Q
R
R
eR
R
,977,0)9846,01(
114
14
1)1(
1
1
1
22*
=−
−−
−
−=−
−−
−
−=
R
kn
n
R
9922,0
2
==
R
R
.
Полученное значение коэффициента детерминации больше, чем 0,75
следовательно, модель можно считать адекватной.
6. Определим значимость параметров модели. Вычислим средние
квадратические отклонения ошибок коэффициентов регрессии:
; 15,0
2
)10(304
301,0
)(
)
)(
1
(
2
2
22
2
2
2
22
0
=
−⋅
⋅
=
∑∑
−
∑
=
∑
−
+=
xx
n
xS
xx
x
n
SS
ii
i
i
a
; 02,0
)10(304
1,04
)()(
22
2
2
2
2
2
1
=
−⋅
⋅
=
∑∑
−
=
∑
−
=
xx
n
nS
xx
s
S
ii
i
a
387,015,0
0
==
S
a
;
.141,002,0
1
==
S
a
Табличное значение Стьюдента
t
2
;
0,025
=4,303. Получаем расчетные
значения Стьюдентов:
0
a
t
=0,5/0,387=1,291;
1
a
t
=1,6/0,141=11,31.
Вывод 2: параметр
a
1
будет значим так, расчетное значение
Стьюдента будет больше, чем табличное, параметр
a
0
– незначим.
Аналогичный вывод можно сделать иначе, вычисляя доверительные
интервалы для параметров модели:

43
a
0
=0,5±4,303·0,387=0,5±1,665;
a
1
= 1,6±4,303·0,141= 1,6±0,607.
Так как абсолютное значение параметра
a
1
будет больше, чем его
доверительный интервал, то параметр значим. Параметр
a
0
незначим.
7.
Оценка среднеквадратического отклонения ошибки
316,01,0
2
=== SS
. Разделив все отклонения (остатки) на эту
величину, получим нормированные отклонения, которые все находятся в
интервале [-2; +2].
Вывод 3: первая предпосылка выполняется, случайная ошибка имеет
нормальный закон распределения с нулевым математическим ожиданием.
8.
Критерий Дарбина-Уотсона вычисляем следующим образом:
DW = ((0,3+0,1)
2
+(–0,3–0,3)
2
+(0,1+0,3)
2
) / 0,2=3,4
1,5 < DW < 4–1,5 (d
в
примерно равно 1,5 (прилож. 3)).
Вывод 4: вторая предпосылка не выполняется, между текущими
значениями случайной величины присутствует отрицательная
автокорреляция.
В завершении работы приведем итоговую таблицу остатков и
нормированных отклонений (табл. 3.4).
Таблица 3.4
N/N Значение Y Оценка Y Остатки Нормированные
отклонения
1
2
3
4
2
4
5
7
2,1
3,7
5,3
6,9
–0,1
0,3
–0,3
0,1
–0,316
0,948
–0,948
0,316
3.7. STATISTICA. ПРОВЕРКА РЕЗУЛЬТАТОВ КОНТРОЛЬНОГО
ПРИМЕРА В MULTIPLE REGRESSION
Для проведения расчетов с модулем предварительной обработки
необходимо выполнить следующие действия:
•
запустите программу STATISTICA командой
Пуск/Программы/Statistica6.0/Statistica;
• в открывшемся окне закрыть все окна документов и выполнить
команду
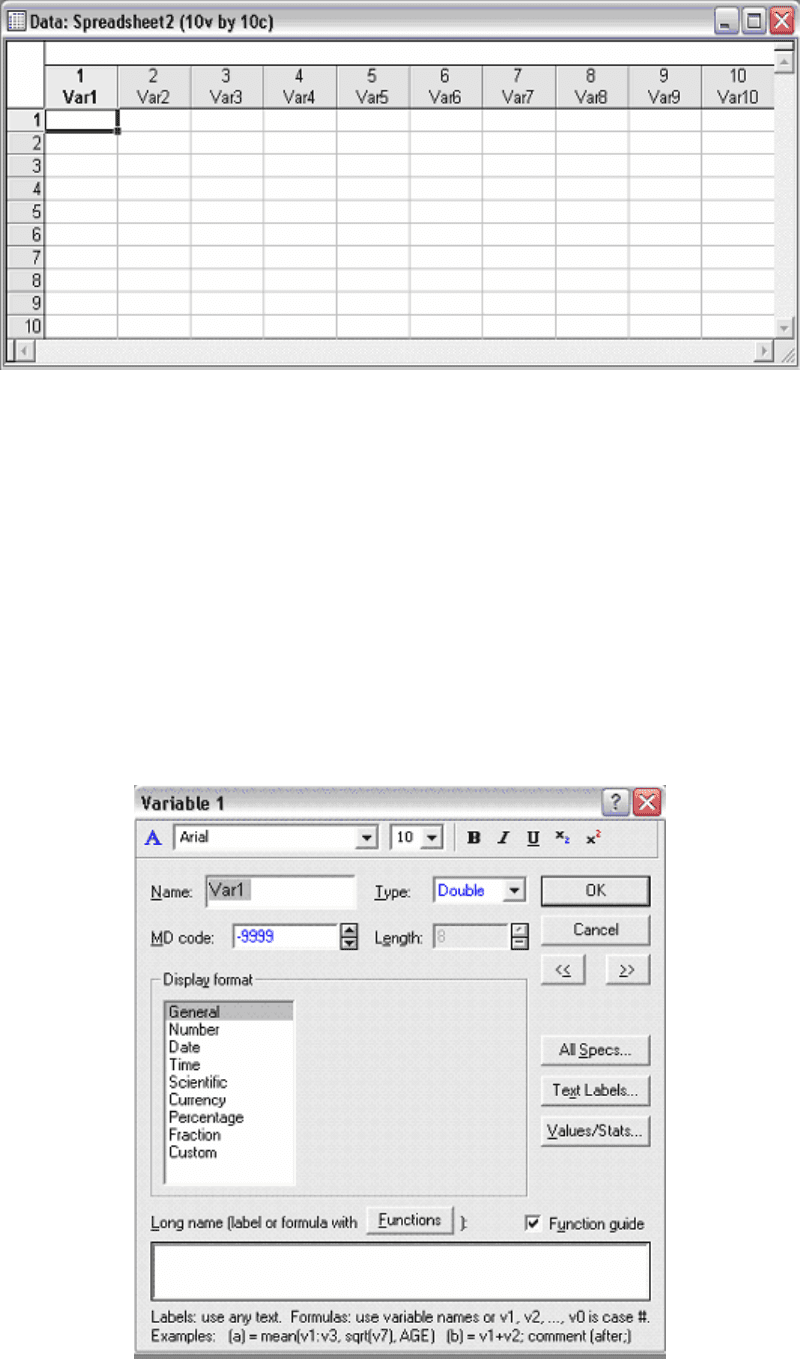
File/New Data. В окне Create New Document указывается число
создаваемых строк и столбцов, по умолчанию создается таблица для ввода
данных размером (10х10) (Рис. 3.1);
44
Рис. 3.1
•
введите исходные данные для переменных X и Y в столбцы VAR1
и VAR2;
•
выделите блок колонок VAR3-VAR10 и нажмите на панели
инструментов кнопку
Vars. В появившемся меню выберите команду
Delete, а затем в диалоговом окне нажмите кнопку OK;
•
выделите блок строк 5–10 и нажмите на панели инструментов
кнопку
Cases. В появившемся меню выберите команду Delete, а затем в
диалоговом окне нажмите кнопку
OK;
•
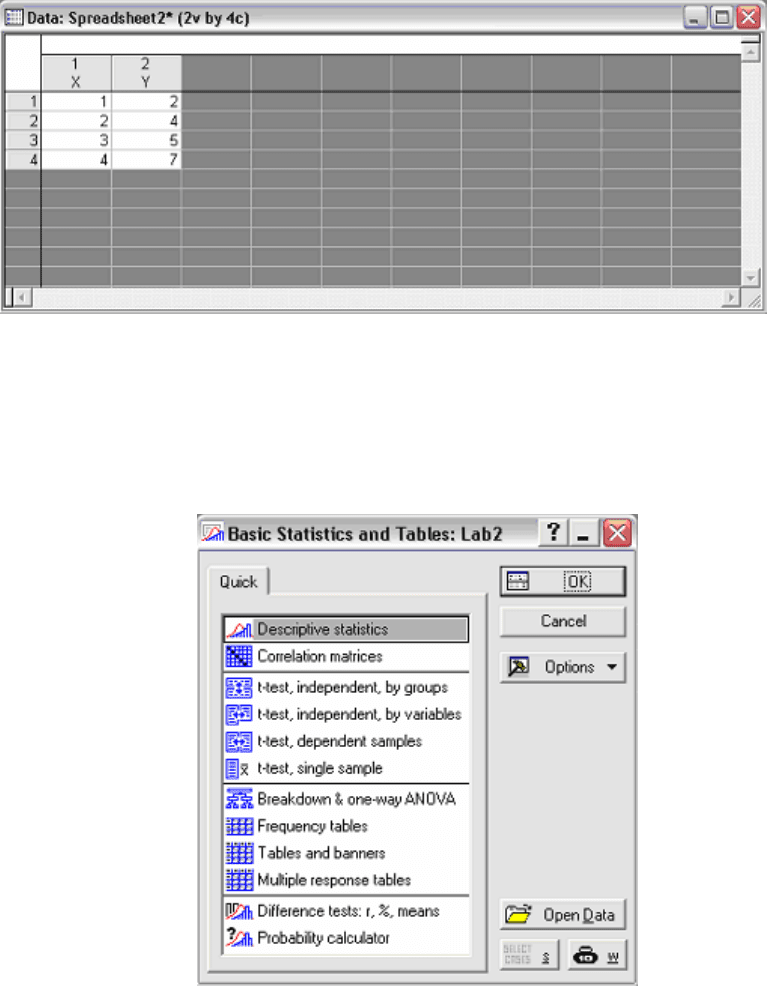
щелкните правой клавишей мыши по столбцу VAR1 и выберите
команду
Variable Specs.... Появится диалоговое окно (Рис. 3.2);
Рис. 3.2
45
•
введите имя переменной X и нажмите OK;
•
аналогичную процедуру проведём со столбцом VAR2;
•
в результате вы должны получить таблицу данных следующего
вида (Рис. 3.3);
Рис. 3.3
•
сохраните полученный файл данных командой File/Save As;
•
сделайте активным окно с таблицей данных, а затем выполните
команду
Statistics/Basic statistics. Появится окно (Рис. 3.4);
Рис. 3.4
•
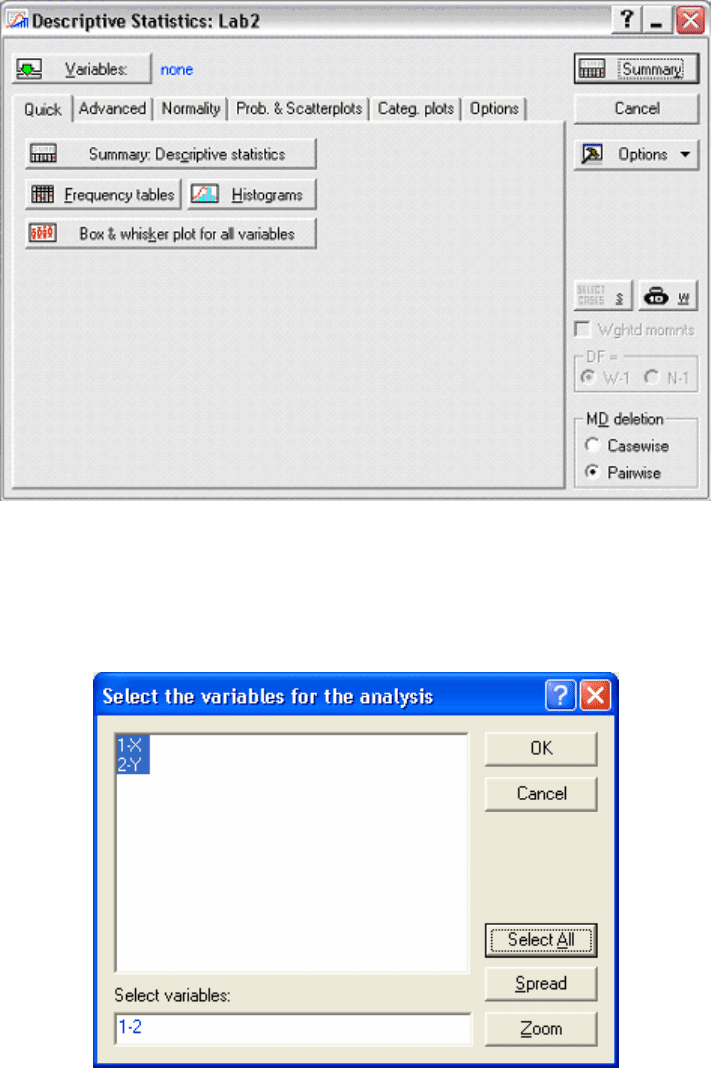
выберете пункт Descriptive statistics и нажмите OK. Появится окно
(Рис. 3.5);
46
Рис. 3.5
•
нажмите кнопку Variables. В появившемся диалоговом окне (рис.
3.6) нажмите кнопку
Select All и OK;
Рис. 3.6
•
программа выполнит переход в предыдущее окно, в котором
необходимо нажать кнопку
Summary: Descriptive statistics. Появится
таблица с результатами расчетов (Рис. 3.7);

47
Рис. 3.7
•
нажмите кнопку Descriptive statistics или Statistics/Resume (Рис.
3.8).
Выполнится переход в предыдущее окно;
Рис. 3.8
•
выберете закладку Prob. & Scatterplots, нажмите кнопку 2D
scatterp.
Появится окно для выбора переменных (Рис. 3.9);
Рис. 3.9
•
сделайте необходимые изменения и нажмите кнопку OK;
48
•
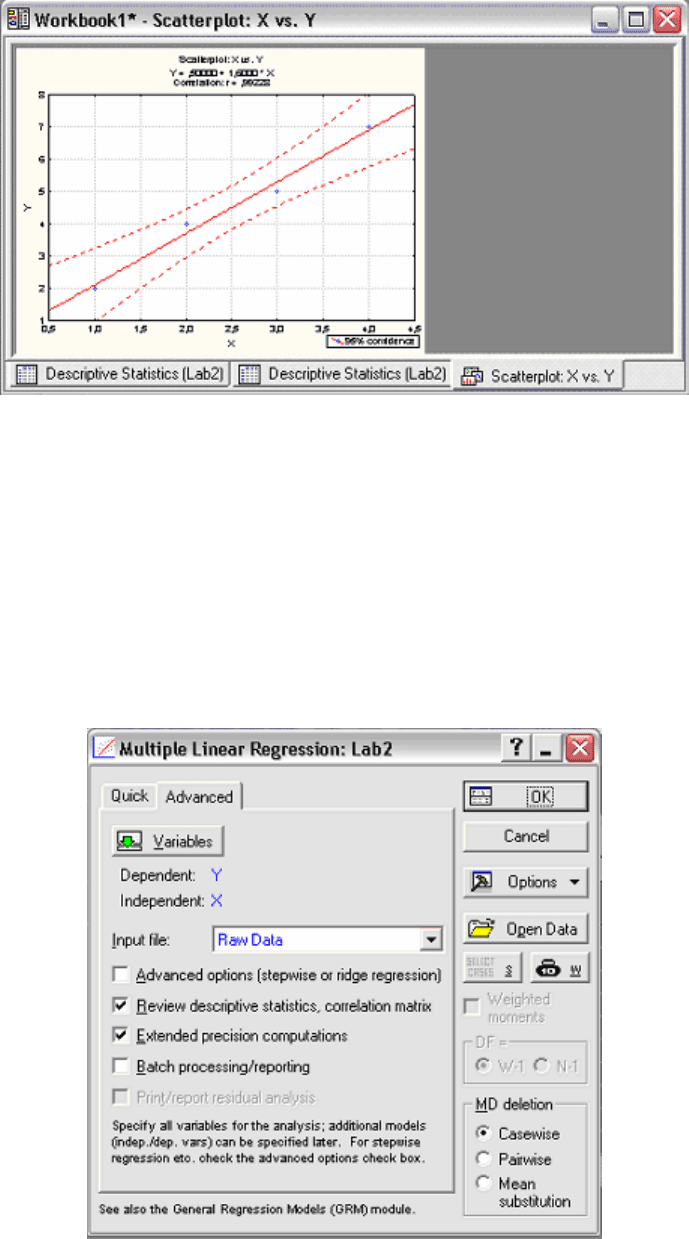
появится окно (Рис. 3.10) с графиком линейной регрессионной
модели, с рассчитанными значениями коэффициентов модели и
коэффициентом корреляции. Первая часть работы выполнена.
Рис. 3.10
Дальнейшие вычисления проводятся с использованием модуля
Multiple Regression, для перехода в который дайте команду Statistics/
Multiple Regression.
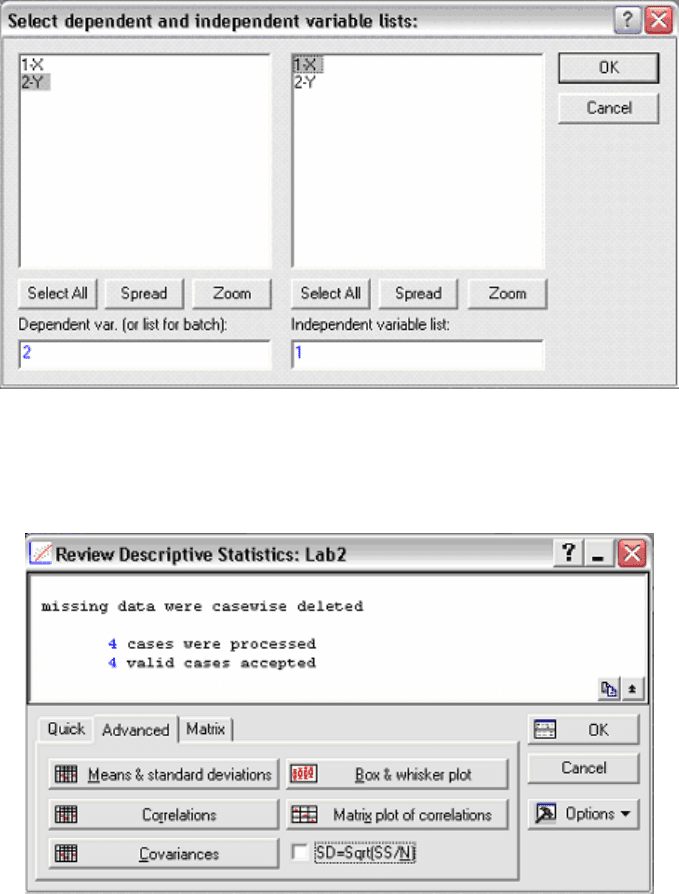
Появится стартовая панель, в которой надо сделать
следующие установки (Рис. 3.11) и определить зависимую (Dependent) и
независимую (Independent) переменные (Рис. 3.12), нажав предварительно
кнопку
Variables.
Рис. 3.11
49
Рис. 3.12
•
после этого в окне Multiple Linear Regression нажмите OK;
•
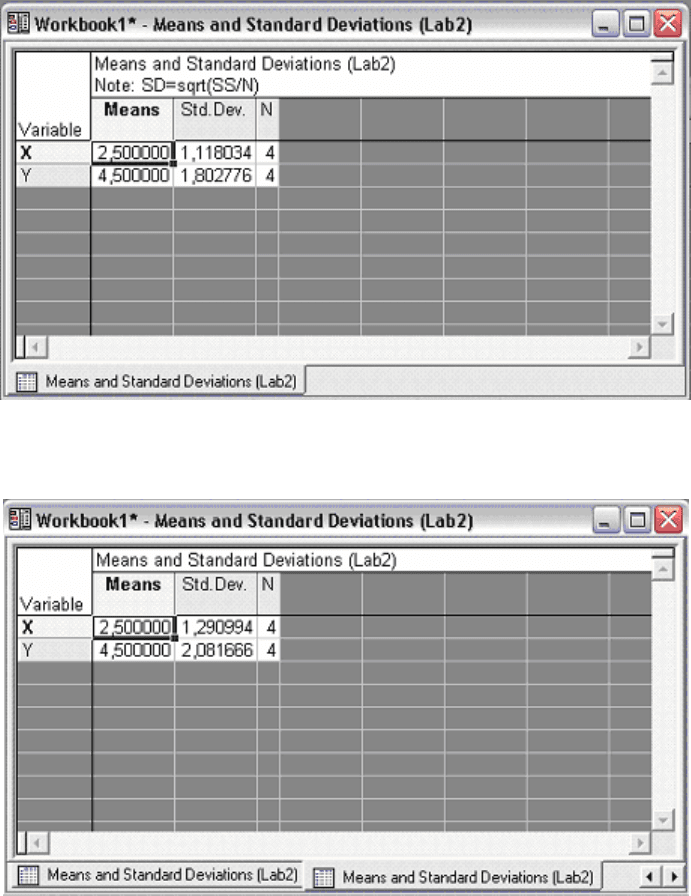
появится окно Review Descriptive Statistics (Рис. 3.13).
Рис. 3.13
•
определим смещенные среднеквадратические отклонения. Для
этого поставьте флажок в поле
SD=Sums of Squares/N и нажмите Means &
Standard Deviations
(Рис. 3.14). Аналогично можно вычислить
несмещенные среднеквадратические отклонения при этом флажок должен
отсутствовать (Рис. 3.15).
50
Рис. 3.14
Рис. 3.15
•
в окне Descriptive Statistics нажмите Correlations для расчета
коэффициента корреляции (Рис. 3.16).
