Lal R., Shukla M.K. Principles of Soil Physics

Подождите немного. Документ загружается.

The fundamental driving forces in both saturated and unsaturated flow are the potential

gradient and hydraulic conductivity. As a stream of water is passed through the

unsaturated soil matrix, the incoming water replaces the air present in the soil pores; it

increases the total volume of water inside the soil, thus increasing the moisture content

(θ) of soil. This agrees with the fundamentals of continuity equation, which states that the

difference in the inflow and outflow rate is equal to the change of water storage in soil.

The gradient causing flow in unsaturated soils is of negative pressure potential. The flow

paths in unsaturated flow are more tortuous as several pores are filled with air. The

hydraulic conductivity in an unsaturated zone can vary by as much as four to five orders

of magnitude. Some of the differences in saturated and unsaturated flow are summarized

in Table 13.1. A typical situation of water in an unsaturated soil media forming separate

and discontinuous pockets of water given in Fig. 13.1 presents magnified pores of

varying diameter. For simplicity the soil particles are sketched as either spheres or

ellipses. The schematic in Fig. 13.1 shows that the empty pores must be circumvented for

the water to flow through the soil matrix. This increases the length of flow path or

tortuosity. Since bigger pores drain quickly most of the air-filled pores are more

conductive, forcing the water to move through only smaller less conductive pores. The

same is also true in aggregated soils, where large interaggregate spaces empty early

leaving the small pores for water flow.

Water has an affinity for soil particle surfaces and capillary pores, which results in

matric suction (Φ

). When Φ

is uniform throughout the soil matrix, the soil system

remains in equilibrium or at a steady state

TABLE 13.1 Summary of Differences Between

Saturated and Unsaturated Flow

Parameter Saturated flow Unsaturated flow

Water content Constant Variable over space and time

Air content Zero (close to zero) Variable over space and time

Potential gradient Positive and constant Negative and variable

Hydraulic conductivity Maximum, constant Low and variable

Vapor flow None Possible provided temperature gradients also exist

Water flow Steady Steady as well as unsteady

Flow paths Continuous Tortuous

Continuity equation Inflow = outflow Inflow = outflow + source or sink, of water

Flow descriptions Darcy’s law Darcy–Buckingham equation Richards equation

Flow parameter K

K(θ)

Principles of soil physics 354

FIGURE 13.1 Schematic of an

aggregated soil.

condition. When Φ

is not uniform within soil profile, water moves from a site of higher

till the system attains equilibrium. Another mechanism operating in the unsaturated

soil system is vapor flow. In situations where there are strong temperature gradients

vapor transport becomes a very important phenomenon (see Chapter 17). Depending

upon the vapor pressure inside the soil matrix, soil water can move from the pockets of

higher to lower moisture content, and vice versa. This is one of the fundamental reasons

why pressure potentials (Φp) and matrix potentials (Φ

) are used for assessing/predicting

soil moisture movement rather than soil moisture content.

13.3 DARCY-BUCKINGHAM EQUATION

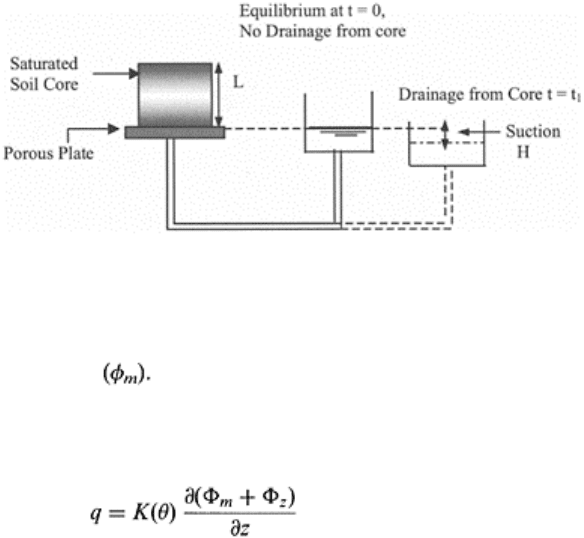
Unsaturated flow through a soil system is illustrated in Fig. 13.2. A saturated soil core is

placed on a porous plate and the reservoir used to saturate the soil core is lowered to a

position below the bottom of soil core. Since the soil core is open to the atmosphere and

the water level in the reservoir is below the bottom of soil core, a Φ

gradient is created

across the soil core. As a consequence, air starts entering the soil core from the top

pushing the water down and out through the bottom into the water reservoir. If the flux

density measured from the bottom of soil core is q, the hydraulic head difference (∆H)

across the core equals (H

−H

) and the hydraulic gradient is ∆H/L.

Flux density, as in the case of saturated flow, is proportional to the driving force (i.e.,

the hydraulic gradient, ∆H/L)

(13.1)

(13.2)

where K(θ) is the unsaturated hydraulic conductivity of the porous medium. This

equation is equivalent to Darcy’s law discussed in Chapter 12. Since Buckingham (1907)

Water flow in unsaturated soils 355

was first to describe hydraulic gradient dependent flow through unsaturated media, Eq.

(13.2) is known as the Darcy–Buckingham equation.

FIGURE 13.2 Schematic of

unsaturated flow across a soil core.

The unsaturated hydraulic conductivity [K(θ)] is dependent on both moisture content

and matric potential

Equation (13.2) can be written in terms of suction (Φ

, or its

negative suction head) and gravitational component (Φ

) as H=Φ

+Φ

. Contrary to

saturated flow, where Φp is a function of z only, in unsaturated flow Φ

is a function of

both z and time (t). Therefore, the derivative ∆H is a partial derivative and Eq. (13.2) can

be written as

(13.3)

where ∂z is change in length (L). The partial derivative of Φ

and Φz implies that

temperature is constant during the experiment.

13.4 UNSATURATED HYDRAULIC CONDUCTIVITY

The unsaturated hydraulic conductivity [K(θ)] is a nonlinear function of both moisture

content and Φ

. Figure 13.3 presents typical curves for sand and a clay soil, and shows

that at higher matric potential (i.e., near saturation, or Φ

→0) the sand or coarse-textured

soil has higher K(θ) compared to clay soils. However, as these soils are desaturated, the

hydraulic conductivity in the coarse-textured soil decreases faster than in fine textured

soil and these two curves cross each other. After that for a given Φ

, the K(θ) of coarse-

textured soil is always lower than fine-textured soil. This seems logical, because coarse-

textured soils have larger pores, which drain faster compared to fine-textured soils, which

have relatively smaller pores. Since a greater number of pores is filled with water in

Principles of soil physics 356

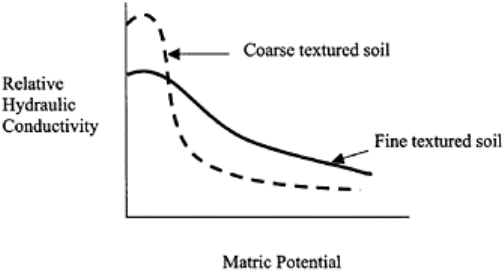
FIGURE 13.3 Schematic of relative

hydraulic conductivity versus matrix

potential for a fine and coarse textured

soil.

fine-textured soil, the tortuosity is less and K(θ) is higher than in coarsetextured soil.

The Darcy–Buckingham equation is applicable to unsaturated flow conditions as long

as moisture content (θ) remains constant over time. However, in most unsaturated flow

situations in nature, it is seldom the case. Under these circumstances, Eq. (13.2) is

combined with the continuity equation, which relates the time dependent rate of change

of θ to the space dependent rate of change of flux density (q) in a small elemental volume

of the soil. When rate of change in moisture content of a soil matrix with respect to time

remains unchanged the flow is called steady flow, and when θ changes with time the flow

is called unsteady flow. While steady state flow can be described by just one equation

[e.g., Eq. (13.2)], two equations are necessary for describing unsteady flow through

porous medium. One is the Darcy–Buckingham equation [Eq. (13.2)] and the other is the

continuity equation.

13.5 CONTINUITY EQUATION

The equation of continuity combines the rate of change of moisture content of soil matrix

to the changes in incoming and outgoing fluxes through the soil matrix. The continuity

equation states that rate of change of incoming and outgoing flux is equal to the rate of

change of storage in the soil matrix. To derive the equation of continuity for a three-

dimensional and one-dimensional flow domain as given in Fig. 13.4, let us consider a

threedimensional element in an incompressible flow domain of sides dx, dy, and dz. The

components of velocities in the flow element are v

, v

and v

. If the volumetric flow rate

per unit cross-sectional area entering from left hand side of the flow domain as shown in

Fig. 13.4, is q.

Water flow in unsaturated soils 357

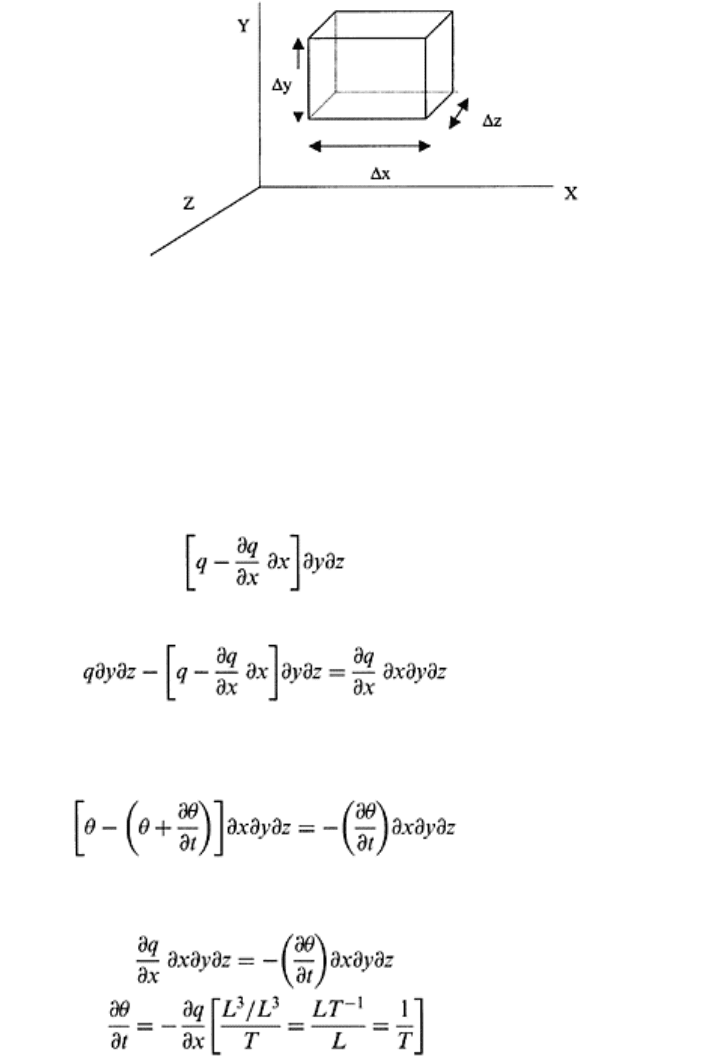
FIGURE 13.4 Water flow through a

three-dimensional section of soil

matrix.

Then the volumetric inflow rate from left to right is:

Inflow =q∂y∂z

(13.4)

Let us assume that volumetric flow rate at the other end of the element is less than the

volumetric inflow rate. So the total outflow rate through the element is:

(13.5)

and the inflow-outflow will be equal to:

(13.6)

Since the outflow is less than inflow, it implies that there is an increase in the moisture

content in the soil element. If the initial moisture content of the soil is θ the rate of

change of moisture content in the flow domain in time t can be expressed as follows

(13.7)

Since the net change in flow is equal to net change in moisture content, the Eqs. (13.6)

and (13.7) are equal

(13.8)

(13.9)

Principles of soil physics 358

Equation (13.9) is the one-dimensional continuity equation. If we consider the volumetric

fluxes in all the three directions (q

, q

, and q

), Eq. (13.9) changes into a three-

dimensional form of continuity equation [Eq. (13.10)].

(13.10)

(13.11)

where

is the vector differential operator for three-dimensional gradient. It can also be

called the spatial gradient of flux. It is also represented as div:

(13.12)

Richards (1931) combined the Darcy–Buckingham Eq. (13.2) and the continuity Eq.

(13.11) to derive the equation of unsaturated flow.

13.6 RICHARDS EQUATION

Under most natural situations, unsteady flow occurs through the soil matrix. The K(θ) is a

function of both moisture content and Φ

, while hydraulic head includes both suction

(Φ

) and gravitational (Φ

) components. Since pressure potentials in unsaturated soils are

negative, the Φ

is used to denote it as a positive quantity. Equation (13.2) can be

reproduced in terms of suction and moisture content as follows:

(13.13)

(13.14)

where K is a function of suction [K(Φ

)] and moisture content [K(θ)]. If the soil suction

is fluctuating, i.e., sometimes increasing and sometimes decreasing, Miller and Miller

(1956) pointed out that the Eq. (13.12) does not hold true because it does not take into

account the hysteresis of soil moisture. However, if suction is omnidirectional (i.e., either

increasing or decreasing continuously) then hysteresis (see Chapter 11) can be ignored.

Transferring the Eq. (13.12) to the one-dimensional continuity Eq. (13.10)

(13.15)

where

(13.16)

Water flow in unsaturated soils 359

Reproducing the continuity Eq. (13.10) here

Transferring Eq. (13.19) into Eq. (13.10), while assuming soil is isotropic

(13.17)

The one-dimensional form of the Richards equation for H=Φ

+Φ

becomes

(13.18)

(13.19)

Eq. (13.19) is known as the Richards equation and was derived in 1931 (Richards, 1931).

If the soil is either wetting or drying then the moisture content (θ) will be uniquely related

to the suction (Φ

). Applying the chain rule (Kaplan, 1984), rate of change of moisture

content can be expressed as

(13.20)

where C

, is known as soil-moisture capacity function (L

−1

), which is equal to the inverse

slope of the soil-moisture characteristic curve or Φ

(θ). It refers to the increase in Φ

per

unit increase in θ. Transferring the soilmoisture capacity function Eq. (13.20) into (13.19)

gives the capacitance form of Richards equation

(13.21)

Alternately suction component can be represented as

(13.22)

Transferring Eq. (13.22) into Eq. (13.19) leads to the diffusivity form of Richards

equation

(13.23)

where soil-water diffusivity D(θ)

(13.24)

Principles of soil physics 360

The dimensions for soil-water diffusivity (D(θ)) from Eq. (13.24) are L

−1

, and it is

defined only in the absence of hysteresis. The first term on the right-hand side in

Richards equation is for flow of water owing to the gradient of Φ

. The second term is

known as gravitational term. Neglecting the gravitational term in Eq. (13.23)

(13.25)

Equations (13.21) and (13.23) are highly nonlinear because of the functions C

(Φ

D(θ), and K(θ) because of their dependence on both Φm and θ. They are also known as

Fokkar–Plank equations. The equations can be solved numerically. Approximate

analytical solutions are also available (Parlange et al., 1997). The soil-water diffusivity

can be assumed constant for a very small range of wetness. This assumption transforms

Eq. (13.25) to a form similar to Fick’s second law of diffusion (See Chapter 18).

(13.26)

The soil-water diffusivity is a complex parameter, and can be misleading. The water flow

through soils is described as mass flow or convection but not diffusion. The hydraulic

diffusivity expression becomes inconsistent whenever hysteresis is predominant or soil is

layered. However, the range of variation of diffusivity is much smaller as compared to

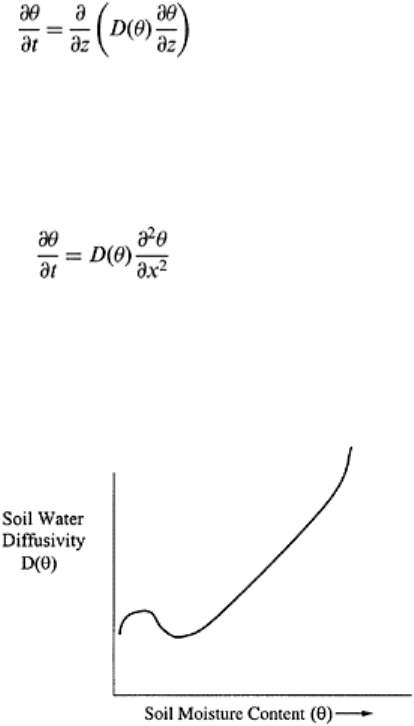
the hydraulic conductivity. The relationship between soil-water diffusivity

FIGURE 13.5 Schematic of the

relationship between soil moisture

content and soil water diffusivity.

and soil-water content is shown in Fig 13.5. It has been observed that initially when soil

is very dry, diffusivity decreases with increasing water content. This is apparently due to

vapor movement (Philips, 1955). Once soil attains certain moisture content, the

relationship becomes positive and linear. However, near saturation, soil-water diffusivity

tends to approach infinity.

Water flow in unsaturated soils 361

13.7 ESTIMATION OF SOIL’S HYDRAULIC FUNCTIONS

The hydraulic conductivity of unsaturated soil can be calculated from the known Φ

and

θ relationship. The schematic of random distribution of pores as proposed by several

authors (Childs and Collis-George, 1950; Marshall, 1958; Millington and Quirk, 1959)

assumes that soil is made up of distinct randomly distributed pores of various radii. The

overall conductance of such a soil system depends upon the geometric configuration and

the number of pairs of interconnected pores. The random distribution of pores is shown in

the Fig. 13.6.

Generally in a soil matrix, smaller pores are more numerous compared to larger pores.

Therefore, smaller pores are more interconnected than larger pores. For a given volume

of soil matrix, the number of pore connections N across any plane is inversely

proportional to the crosssectional area of pore. If r is the radius of a pore then N is

1/r

Poiseuille’s law relates the volumetric flow rate of the pore (Q) to the fourth power of

FIGURE 13.6 The random distribution

of pores in a section of soil.

radius of a pore as Therefore, overall conductance of soil due to each class of

pores (K) can be given as

(13.27)

By dividing and measuring the porosity of soil into several distinct classes, we can obtain

the probability that a pore of various radii connects a pore of larger or smaller radius.

Thus, we can obtain the conductivity values for different degrees of saturation. In

practice, a soil-mositure characteristic curve (SMCC) divides porosity into pore-size

classes and corresponding partial volumes, thus suction is related to moisture content.

The suction can also be related to pore radius by capillary equation (r=2σ/ Φ

, where Φ

is the capillary rise). The SMCC can be divided into pore radii increments and

corresponding moisture volume increments. Using this technique, the K(θ) can be

calculated by the Childs and Collis-George (1950) method:

(13.28)

Principles of soil physics 362

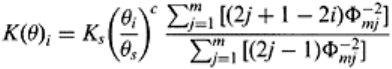
where ρ

is density of water, η

is viscosity of water, f(Γ) dr the partial area occupied by

pores of radii Γ to Γ dr and f(δ) dr the partial area of pores with δ dr. The F in Eq. (13.28)

is a matching factor, which is required to fix the hydraulic conductivity value to an

experimentally predetermined K(θ) value for a known θ. In the Childs and Collis-George

procedure the calculations are made successively for different values of wetness. For

each case the summation terminates at the largest pore radius R, which is water filled at a

specific value of soil wetness. The calculations for Childs and Collis-George procedure

are cumbersome, but the K(θ) function is reportedly close to measured K(θ) function for

sand and slate dust. Marshall (1958) and Millington and Quirck (1959), Kunze et al.

(1968), and Jackson (1972) further simplified the calculation procedure. Changing the

matching factor to the ratio of measured saturated hydraulic conductivity (K

) and

calculating saturated hydraulic conductivity Reference, Jackson (1972) gave the

following formulation.

(13.29)

where K(θ)

is the hydraulic conductivity at a moisture content of θ

, m is the number of

increments of θ, Φ

is the suction head at the mid-point of each of θ increment, and C is

an arbitrary factor which is reported to be 0–4/3.

13.7.1 Measurement of Soil’s Hydraulic Functions

Soil’s hydraulic functions can be estimated both in the lab and field by various methods,

which can be classified as: (i) steady flow methods and (ii) unsteady flow methods. In the

steady state methods for the determina-tion of K(θ) and D(θ), flux, gradient, and moisture

content remain unchanged. However, in transient state methods, all three vary by

parameter. Klute and Dirksen (1986) described the laboratory methods for the

measurement of K(θ) and D(θ).

13.7.2 Laboratory Method

The laboratory methods are (i) steady state and (ii) transient methods. Steady state

methods are those where a mean Φ

is related to the mean θ of the soil in a core or

column. Proper adjustments are made to account for the hydraulic resistance of porous

media at the inlet end of the core. Transient methods include the infiltration method and

pressure outflow method. The infiltration method is based on the principle that at t→∞,

the steady rate of inflow into a soil (q) tends to be equal to K(θ) (q→K(θ)) for

homogeneous moisture content of soil profile (0

). A series of measurements for q with

respect to time, under different Φ

provides the relationship between Φ

, θ and K(θ)

(Davidson et al., 1963; Youngs, 1964). A schematic of setup for the measurement of

unsaturated hydraulic functions is given in Fig. 13.7.

Laboratory determination of K(θ) and D(θ) can also be made in long soil columns by

inducing evaporation (Moore, 1939) or infiltration (Youngs, 1964). A series of

measurements of suction gradient and moisture content can be made on a long soil

Water flow in unsaturated soils 363