Lal R., Shukla M.K. Principles of Soil Physics
Подождите немного. Документ загружается.

The application of Eq. (16.24) or (16.26) to transport through laboratory soil columns or
in fields having relatively uniform soils involving nonreactive or weakly reactive solutes
was found to be fairly successful (Biggar and Nielsen, 1976; Jaynes, 1991; Ellsworth et
al., 1996; Shukla et al., 2003). The BTCs for these tracers are symmetrical and mass
recoveries are relatively high (Fig. 16.7). However, for strongly adsorbed chemicals and
aggregated soils these equations do not perform very well (van Genuchten and Wierenga,
1976; Nkedi-Kizza et al., 1984).
During solute transport in heterogeneous soils, the assumption of local equilibrium
implies instantaneous interchange of mass, large residence time sufficient to make
concentration gradients negligible, and high degrees of interactions between macroscopic
transport properties and microscopic soil
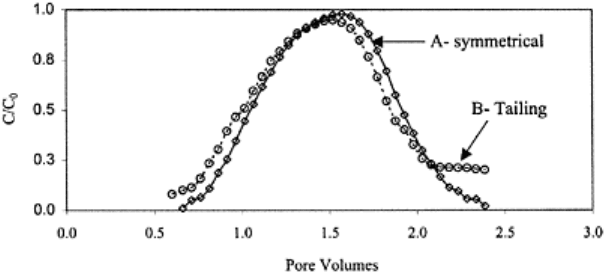
FIGURE 16.7 Schematic of
equilibrium and nonequilibrium
transport of a tracer through laboratory
soil columns, the ETC “A” is
symmetrical and mass recoveries are
higher than a asymmetrical ETC “B”.
physical properties. Some of the macroscopic transport properties are water flux,
apparent dispersion, and moisture content, and microscopic properties are aggregate size,
exchange, pore geometry. The microscopic properties impose a rate limiting effect on
solute transport through heterogeneous soils and deviations from local equilibrium
conditions are observed. The mass recoveries, for these asymmetrical and nonsigmoidal
concentration distributions or BTCs, are less and the BTCs have a long tail (Fig. 16.7).
Such a deviation is caused by a number of physical and chemical nonequilibrium
processes. The physical nonequilibrium is caused by a heterogeneous flow regime and a
chemical nonequilibrium by the kinetic adsorption. This paves the way for the
examination of diffusion controlled or chemically controlled kinetic rate reactions or both
of the form ∂S/∂t=f(S
s
, C). The following sections will examine briefly the
nonequilibrium processes arising out of physical or chemical nonequilibrium.
Principles of soil physics 454
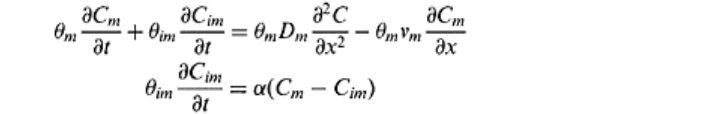
16.13 TWO-REGION NONEQUILIBRIUM TRANSPORT MODEL
There are several factors responsible for physical nonequilibrium conditions occurring in
a soil system during solute transport. Some of them are: (i) heterogeneity of pore size
distribution or aggregation; (ii) heterogeneous diffusion into the Neurst film of water
surrounding soil particles than soil bulk solution. Physical nonequilibrium is represented
by a two-region (dual porosity) type formation. In this case, the medium is assumed to
contain two distinct mobile (flowing) and immobile (stagnant) liquid regions. The
simplest explanation of a two region mobile and immobile formation is the water inside
an aggregated soil. All the intraaggregate water held within an aggregate is immobile and
the interaggregate (between aggregates) water is mobile. The water flowing around dry
aggregates imbibes them and solute entry inside aggregate is by convection. For moist
aggregate, solute entry is governed by diffusion. However, there must be a concentration
gradient from outside to the inside of an aggregate, and a first-order process can
adequately describe the mass transfer between the two regions. In a two-region model,
convective diffusion transport is assumed to take place in the mobile region while
transfer of solutes into and out of mobile region is assumed to be diffusion controlled.
One-dimensional unsaturated flow of conservative nonsorbing solute in a soil is given as
follows (Coats and Smith, 1964):
(16.37)
(16.38)
where t is time (T); C
m
and C
im
are the solute concentrations in the mobile and immobile
liquid phases (ML
−3
) with corresponding volumetric moisture contents θ
m
and θ
im
(L
3
/L
3
)
respectively; D
m
is apparent diffusion coefficient of mobile liquid phase (L
2
T
−1
); x is the
distance from the inflow boundary in the direction of flow (L); v
m
is the average mobile
pore water velocity in (LT−
1
); and a is the first order rate coefficient (T
−1
).
In Eqs. (16.37) and (16.38) as the ratio of mobile water fraction (θ
m
) to total moisture
content (θ) increases (i.e., θ
m
increases), more and more of the wetted pore space is
included in the transport, which causes greater and more complete mixing, and the ETC
shifts further to the right. At the extreme end, the θ
m
=θ, where the above equation reduces
to one-dimensional CDE [Eq. (16.23)]. The parameter α, which has the dimensions of
T
−1
, can vary from 0 to ∞. A zero value of a indicates no mixing between mobile and
immobile water fractions. Therefore, the term on left-hand side of Eq. (16.38) equals zero
and Eq. (16.37) reduces to one-dimensional CDE, similar to Eq. (16.23) but with total
moisture content of θ
m
. When a=∞, the two concentrations mix instantaneously and
C
m
=C
im
. In this case Eq. (16.37) reduces to Eq. (16.23).
One-dimensional solute transport for an exchanging solute during steady-state flow
through a homogeneous porous medium, where the liquid phase is presumed to consist of
a mobile and immobile region and includes a Freundlich-type equilibrium adsorption-
desorption processes (van Genuchten and Wierenga, 1976) can be described by a two-
region model as follows:
Solute transport 455

(16.39)
and
(16.40)
where S
sm
and S
sim
are concentration of adsorbed phase in mobile and immobile phase
respectively (MM
−1
); R
m
and R
im
are retardation factors accounting for equilibrium type
adsorption processes in mobile and immobile regions, respectively; and
parameter/represents the mass fraction of solid phase that is in direct contact with the
mobile liquid phase. If the exchange process in both the dynamic (S
sm
) and stagnant (S
sim
)
region is assumed to be instantaneous, linear and reversible process (van Genuchten,
1981) then,
S
sm
=K
D
C
m
and S
sim
=K
D
C
im
(16.41)
and the total adsorption can be represented by
S
s
=fS
sm
+(1−f)S
sim
(16.42)
For equilibrium adsorption, transferring these into Eqs. (16.39) and (16.40) results in
following set of equations
(16.43)
(16.44)
16.14 TWO-REGION ANION EXCLUSION MODEL
The two-region anion exclusion model divides the total soil-water phase into two
compartments, (i) mobile water and (ii) immobile water, and anion exclusion is assumed
to take place in the immobile region (van Genuchten, 1981). This assumption is
analogous to the assumptions made by Krupp et al. (1972), as anion exclusion takes place
in the smaller pores inside the dense aggregate or in the immobile water along the pore
wall. An equivalent exclusion distance (d
ex
) exists near the pore wall where concentration
remains zero. Therefore, specific exclusion volume (V
ex
; cm
3
water g
−1
of soil) is related
to specific surface area (A
m
; cm
2
g
−1
) and d
ex
as follows:
V
ex
=d
ex
A
m
(16.45)
Principles of soil physics 456
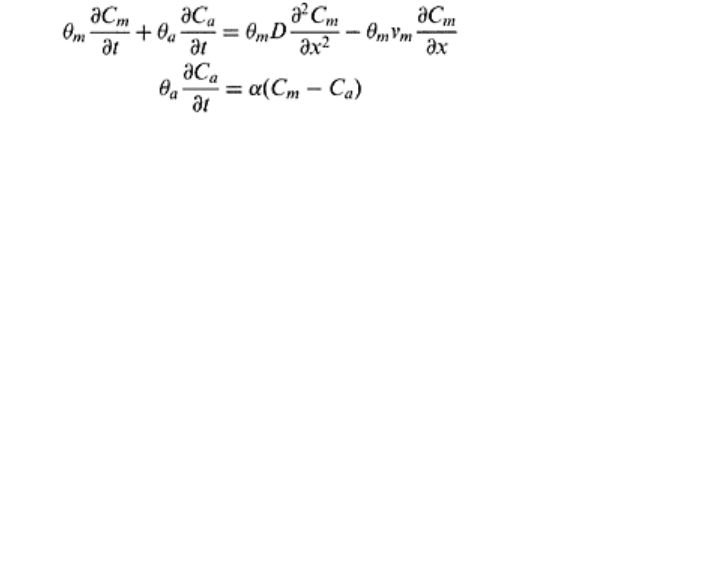
The θ
ex
is obtained by multiplying Eq. (45) by soil bulk density (ρ
b
)
θ
ex
=V
exρb
(16.46)
The part of liquid phase unaffected by anion exclusion (θ
a
) can be calculated as follows:
θ
a
=θ
im
−θ
ex
(16.47)
Using Eq. (16.47), the following physical nonequilibrium equation representing the anion
exclusion process is obtained (van Genuchten, 1981)
(16:48)
(16.49)
where C
a
is concentration in the part of immobile zone unaffected by exclusion. The
model described above assumes anion exclusion taking place inside the immobile water
zone. Therefore, convective transport in mobile zone remains unaffected by the exclusion
process and C
m
never exceeds input concentration C
0
(van Genuchten, 1981).
16.15 TWO-SITE NONEQUILIBRIUM TRANSPORT MODEL
Considering that the solid phase of soil is made up of various constituents (i.e., soil
minerals, organic matter, aluminum, and iron oxides), and chemical react with these
different constituents at different rates and intensities. Selim et al. (1976) and Cameron
and Klute (1997) proposed a two-site chemical nonequilibrium model where adsorption
term consists of two components, equilibrium adsorption, and first-order kinetics. The
sorption or exchange sites in this model are assumed to have instantaneous adsorption
(type-1 sites) and time-dependent kinetic adsorption (type-2 sites). At equilibrium,
adsorption on both types of sorption sites is described by the following linear equations:
S
s1
=K
De
C=FK
D
C
(16.50)
S
s2
=K
Dk
C=(1−F)K
D
C
(16.51)
where subscript “e” refers to type 1 or equilibrium site and subscript “k” refers to type 2
or kinetic sites, respectively, and F is the fraction of all sites occupied by type 1 sorption
sites. Total adsorption at equilibrium is
S
s
=S
se
+S
sk
(16.52)
Because type 1 sites are always at equilibrium therefore,
Solute transport 457
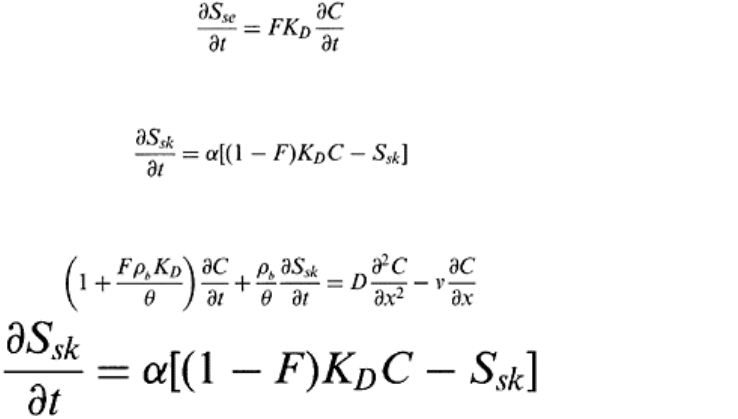
(16.53)
The adsorption rate for type 2 kinetic nonequilibrium sites can be given by a linear and
reversible first order equation of following form
(16.54)
where α is the first order rate coefficient. Combining above equations with Eq. (16.14)
lead to following formulation (van Genuchten, 1981; Nkedi-Kizza et al., 1984):
(16.55)
(16.56)
16.16 INITIAL AND BOUNDARY CONDITIONS FOR STEP
INPUT EXPERIMENTS
The analytical solutions of Eqs. (16.23), (16.24), (16.25), (16.43), (16.44), (16.48),
(16.49), (16.55), and (16.56) are available for a large number of initial and boundary
conditions for both finite and semi-infinite systems for both step and pulse type solute
application (van Genuchten 1981, van Genuchten and Alves, 1982). This section briefly
describes some of the initial and boundary conditions required for solving solute transport
equations. The most common initial condition for any soil is:
C(x, 0)=C
i
(16.57)
At the upper boundary of the soil surface or (or inflow into the soil column; i.e. at x=0),
two different boundary conditions can be considered. The first type or constant
concentration boundary condition is of the form as follows:
C(0, t)=C
0
(16.58)
For column displacement experiments, where chemical is applied at a constant rate, the
boundary condition (16.58) leads to mass balance errors, which become quite significant
for large values of (D/v) (van Genuchten, 1981, Parker and van Genuchten, 1984). The
other boundary condition is a third type, or constant flux type, that leads to the
conservation of mass inside the soil column provided dispersion outside the soil can be
ignored is given as follows:
Principles of soil physics 458
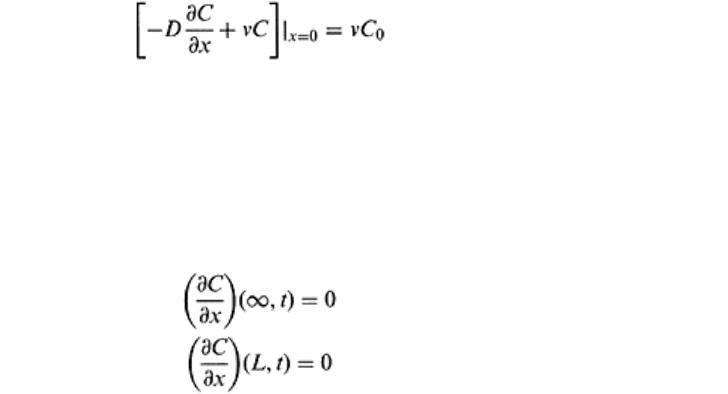
(16.59)
A third type inlet condition is usually preferred over first type inlet condition (van
Genuchten and Parker, 1984, Toride et al., 1993). In order to describe the outlet
conditions, it is assumed that the concentration is macroscopically continuous at the
outlet and no dispersion occurs outside the soil. Parker and van Genuchten, (1984)
suggested that by assuming that the upstream solute concentrations are not affected by
the outlet boundary, solutions for an infinite outlet condition can be applied to the finite
region. The outlet condition for a semi infinite profile (0≤x<∞) and a finite system of
length L can be specified in terms of zero concentration gradient as below
(16.60)
(16.61)
The boundary condition [Eq. (16.60)] assumes a semi-infinite soil column and is
commonly used. When effluent curves from finite columns are calculated using analytical
solutions based on boundary condition [Eq. (16.60)], some errors may be introduced.
Therefore, zero concentration gradient at the upper end of the column as specified by Eq.
(16.61) is frequently used for column displacement studies. However, there is no
evidence available to prove that the boundary condition Eq. (16.61) leads to a better
description of physical processes at and around x=L. On the other hand, the boundary
condition [Eq. (16.59)] gives a discontinuous distribution at the inlet, which is against the
requirement of a continuous distribution at x=L (van Genuchten, 1981).
16.17 DIMENSIONAL INITIAL AND BOUNDARY CONDITIONS
FOR PULSE APPLICATION
Assuming that the concentrations are continuous across the inlet boundary and that input
solution is well mixed, a first type boundary condition across the inlet boundary for a
pulse type injection can be specified as (van Genuchten, 1981):
C(0, t)=C
0
0<t<t
0
C(0, t)=0t>t
0
(16.62)
A third type boundary condition for the pulse input for a well mixed input solution can be
specified as
[−D(∂C/∂x)+vC]|
x=0
=vC
0
0<t≤t
0
[−D(∂C/∂x)+vC]|
x=0
=0 t>t
0
(16.63)
The two-site model [Eqs. (16.55) and (16.56)] can be solved for the boundary and initial
conditions given by Eqs. 16.57 to 16.61. One additional initial condition for the solution
is
Solute transport 459
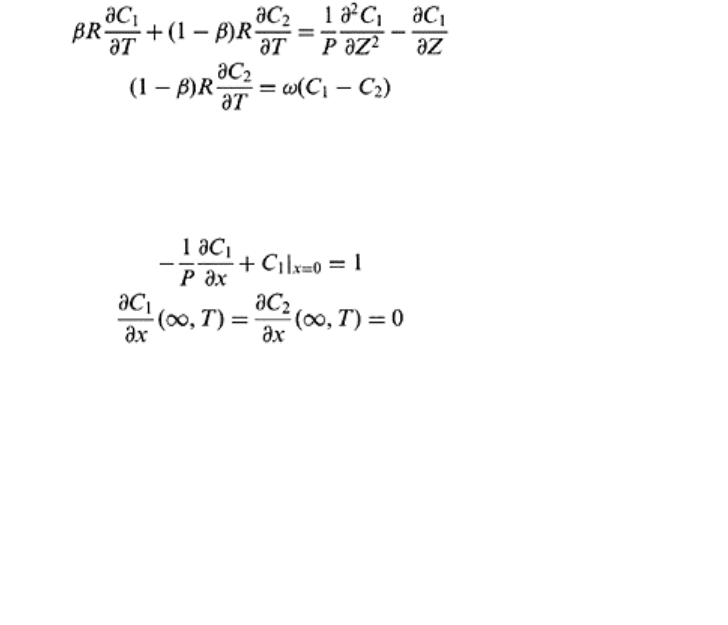
S
sk
(x, 0)=(1−F)K
D
C
i
(16.64)
The initial condition and the boundary conditions at exit remain the same as described by
Eqs. (16.52), (16.55), and (16.56). The boundary condition at inlet, Eq. (16.57), becomes
inappropriate when the input solution is not well mixed. Other arguments against the
applicability of Eq. (16.57) can be that the plane considered as a macroscopic boundary
has no physical relevance at the microscopic level, as irregularity in pore structure and
morphology become manifest at this level. Also the medium properties vary continuously
over a finite transition zone of l/2, where l is the representative elementary volume (REV)
of the porous medium (Parker and van Genuchten, 1984).
16.18 THE COMBINED NONDIMENSIONAL TRANSPORT
EQUATIONS
Nonequilibrium transport Eqs. (16.31), (16.32), (16.36), (16.37), (16.43), and (16.44) are
mathematically equivalent and transferring nondimensional quantities listed in Table 16.4
reduces them to the following combined nondimensional equations (van Genuchten,
1981; Nkedi-Kizza, 1984)
(16.65)
(16.66)
where β is partition coefficient, ω is nondimensional mass transfer parameter and P is
peclet number. Initial and boundary conditions for a step type input are
C
1
(x, 0)=C
2
(x, 0)=0
(16.67)
(16.68)
(16.69)
For β=1, Eqs. (16.65) and (16.66) reduce to the nondimensional CDE. Some of the
analytical solutions of Eqs. (16.17), (16.65), and (16.66) are given in Table 16.5.
16.19 ESTIMATION OF SOLUTE TRANSPORT PARAMETERS
The equilibrium solute transport equation [refer to Eq. (16.17)] has two parameters: (i)
the apparent diffusion coefficient (D) or P (vL/D) and (ii) the retardation factor (R).
TABLE 16.4 Nondimensional Variables
Introduced in the Solute Transport Equations
Principles of soil physics 460

The nondimesional variables
FOR ALL THE EQUATIONS
FOR TWO REGION EQUATION
FOR TWO REGION EQUATION
C
1
=C
m
/C
0
C
2
=C
m
/C
0
q=θ
m
v
m
Source: Modified from van Genuchten, 1981.
TABLE 16.5 Analytical Solutions of Equilibrium
CDE and Nonequilibrium (NE) Transport
Equations
s
ionless
tration
Concentration-type boundary conditions Flux-type boundary conditions
C
1
(0, T)=1
e
Solute transport 461

-
d
els
τ)
)
u
rce: Modified from van Genuchten, 1981.
16.19.1 Retardation Factor (R)
From Measured Breakthrough Curve
The retardation factor (R) can be estimated by locating the number of pore volumes
(T=R) at which the relative concentration of the measured ETC is 0.5. For the measured
chloride ETC in Fig. 16.8, the value of T at C/C
0
of 0.5 is 1.2. Therefore, the value of R is
also 1.2. Both pore volumes (T) and retardation factor (R) are dimensionless.
From Batch Experiment
The batch experiments for solute adsorption are performed by mixing air-dried soil and
solution (1:1). At least six different initial solution concentrations, which are within the
experimental range, are usually selected. Generally three to four replications for each
concentration are made. The mixture is stirred, and after equilibrating for 24 hours, is
centrifuged and the concentration of the extracted solution is measured. The difference
between the initial solution concentration and that in the supernatant (centrifuge) is
assumed to be the result of adsorption. A graph is plotted between the solution
concentration and the adsorbed concentration (Fig. 16.6) and the slope of the line gives
the value of distribution coefficient (K
D
) The R can be calculated from Eq. (16.18) for
known values of bulk density and water content of soil in the experiment.
Principles of soil physics 462
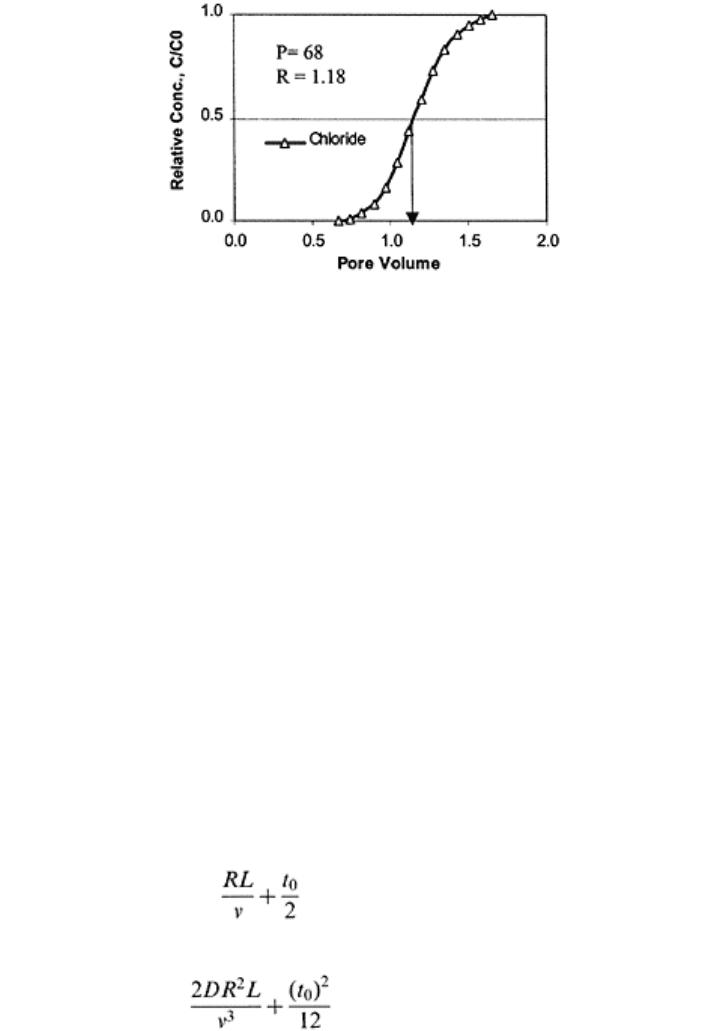
FIGURE 16.8 The estimation of
retardation coefficient from a
measured ETC (R=T=1.2) where T is
pore volumes. (Redrawn from Shukla
and Kammerer, 1998.)
By Fitting Flow Velocity
The pore water velocity can be used as a fitting parameter in the trial and error method
while keeping R a constant and equal to 1. Therefore, fitted velocity will effectively be a
v/R value. The slope of the plot between fitted and measured pore water velocity gives an
effective R-value.
From Travel Time Analysis
Time moment analysis provides a model independent tool for characterizing the solute
BTCs. The first temporal moment provides the mean break-through time, the second
central temporal moment (i.e., the variance) describes the solute spreading, and the third
(skewness) describes the degree of asymmetry of the BTCs (Valocchi, 1985). These
numerical estimates can be compared to the CDE theoretical travel time moments to
provide estimates of the CDE model parameters, in contrast to least-squares fitting of the
analytical solution to Eqs. (16.23) and (16.24). For a finite pulse, the expected or
theoretical mean travel time to depth L is:
(16.70)
and the theoretical travel time variance is
(16.71)
Solute transport 463
