Langetepe E., Zachmann G. Geometric Data Structures for Computer Graphics

4. Given a query (a shape), compute its feature vector and retrieve the nearest neighbor from the

database. Usually, the system also retrieves all k nearest neighbors. Often, you are not interested

in the exact k nearest neighbors but only in approximate nearest neighbors (because the feature

vector is an approximation of the shape anyway).

The main difference among most shape-matching algorithms is, therefore, the transformation from shape

to feature vector.

So, fast shape retrieval essentially requires a fast (approximate) nearest-neighbor search. We could stop

our discussion of shape matching here, but for sake of completeness, we will describe a very simple

algorithm (from the plethora of others) to compute a feature vector [Osada et al. 01].

The general idea is to define some shape function f(P

…

, P

) → , which computes some geometrical

property of a number of points, and then evaluate this function for a large number of random points that

lie on the surface of the shape. The resulting distribution of f is called a shape distribution.

For the shape function, there are a lot of possibilities (your imagination is the limit). There are some

examples:

 f(P

, P

) = |P

− P

 f(P

) = |P

− P

|, where P

is a fixed point, such as the bounding box center,

 ,

 f(P

, P

) = volume of the tetrahedron between the four points.

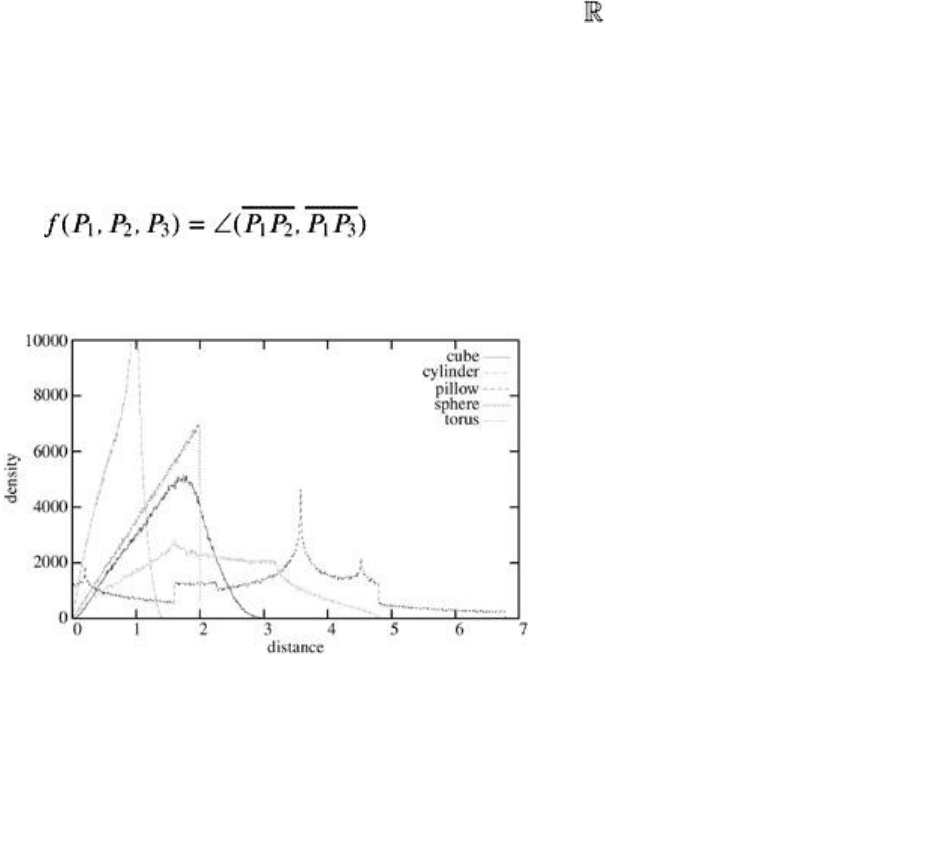
Figure 2.15 shows the shape distributions of a few simple objects with the distance between two points as

shape function.

Figure 2.15: The shape distributions of a number of different simple objects. (See Color Plate XX.)

[3]

This idea seems to originate from image database retrieval, where it was called QBIC, for query by

image content.