Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_137 next page >

Page 137

•

• .

•

These four sets can easily be calculated from a regular expression by using the inductive nature of the

construction of regular expressions. The following lemma accomplishes this. We leave the proofs as

exercises.

Lemma 6.2.3

Let A be an alphabet and let L and M be languages over A.

(i)

•

for each

;

•

; δ(ε)

ε;

•

(

δ(L)

δ(M);

•

δ(LM)

δ(L)

δ(M);

•

δ(L

)

(ii)

•

P(a)

a for each ;

• ; ;

•

(

P(L)

P(M);

•

P(LM)

P(L)

δ(L)P(M);

•

P(L

)

P(L)

(iii)

•

S(a)

a for each ;

•

(

S(L)

S(M);

•

S(LM)

S(M)

S(L)δ(M);

•

S(L

)

S(L)

(iv)

•

for each ;

< previous page page_137 next page >

< previous page page_138 next page >

Page 138

•

(

F(L)

F(M);

•

F(LM)

F(L)

F(M)

S(L)P(M);

•

F(L

)

F(L)

S(L)P(L)

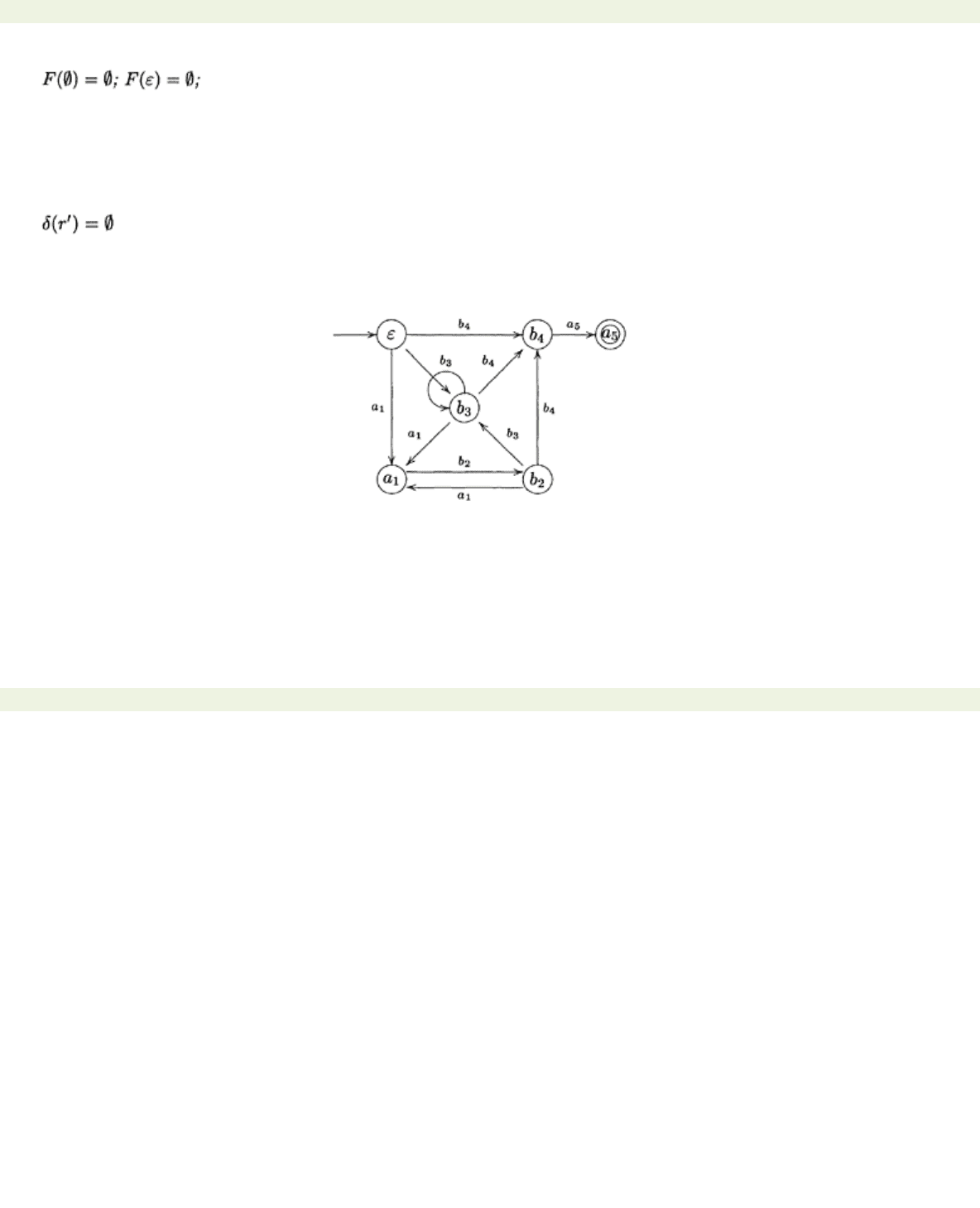
Example 6.2.4 We use Algorithm 6.2.2 together with Lemma 6.2.3 to construct a non-deterministic

automaton recognising the language described by

. First put

r′

3)*

5. We can

easily calculate the following:

•

P(r′)

•

S(r′)

•

F(r′)

We now have the data necessary to construct a standard local automaton recognising

L(r′):

The automaton for

L(r)

is now obtained from this automaton by simply erasing all the subscripts on the

transition labels.

Exercises 6.2

1. Prove Lemma 6.2.3.

2. Use Algorithm 6.2.2 to find non-deterministic automata that recognise the following languages.

(i)

)

(ii) (

)*.

(iii)

(bca

)

< previous page page_138 next page >

< previous page page_139 next page >

Page 139

6.3 Summary of Chapter 6

•

Local languages:

A local language is one in which all strings, apart from possibly the empty string,

begin with certain letters, do not contain consecutive pairs of letters from a list of forbidden factors, and

end with certain letters. Such languages are accepted by Myhill graphs (apart from any identity) or by

local automata. Every recognisable language is the image of a local language under a strictly alphabetic

monoid homomorphism.

•

Linear regular expressions:

A regular expression is linear if each letter occurs exactly once. The

languages described by such regular expressions are local. There is an algorithm that converts a linear

regular expression

into a deterministic local automaton A recognising

L(r)

. This algorithm can be used

to construct a non-deterministic automaton recognising

L(r)

where

is any regular expression.

6.4 Remarks on Chapter 6

I have relied heavily on the paper by Berstel and Pin [13] to write this chapter. Algorithm 6.2.2 is due to

Berry and Sethi [11]. Local languages themselves seem to have been independently discovered by

Myhill [97] and Chomsky and Schützenberger [30]; local automata are also termed ‘Glushkov automata’

[55]. My source for Myhill graphs was Brauer [16]. The paper by McNaughton and Yamada [86]

introduced the idea of labelling the letters occurring in a regular expression.

< previous page page_139 next page >

< previous page page_140 next page >

Page 140

This page intentionally left blank.

< previous page page_140 next page >

< previous page page_141 next page >

Page 141

Chapter 7

Minimal automata

We have so far only been concerned with the question of whether or not a language can be recognised

by a finite automaton. If it can be, then we have not been interested in how efficiently the job can be

done. In this chapter, we shall show that for each recognisable language there is a smallest complete

deterministic automaton that recognises it. By ‘smallest’ we simply mean one having the smallest

number of states. As we shall prove later in this section, two deterministic automata that recognise the

same language each having the smallest possible number of states must be essentially the same; in

mathematical terms, they are isomorphic. This means that with each recognisable language we can

associate an automaton that is unique up to isomorphism: this is known as the minimal automaton of

the language. This automaton plays a crucial role in Chapters 9–12.

There are two different ways of constructing the minimal automaton of a recognisable language

. The

first starts with a deterministic automaton A recognising

and converts it into the minimal automaton

by means of two steps: removal of inaccessible states, introduced in Section 3.1, and ‘reduction,’ a new

process, which involves combining states. The second starts with a regular expression for

and

constructs the minimal automaton using a process called the ‘Method of Quotients.’

7.1 Partitions and equivalence relations

A collection of individuals can be divided into disjoint groups in many different ways. This simple idea is

the main mathematical tool needed in this chapter and forms one of the most important ideas in

algebra.

Let

be a set. A

partition

is a set

of subsets of

satisfying the following three conditions:

(P1) Each element of

is a non-empty subset of

(P2) Distinct elements of

are disjoint.

< previous page page_141 next page >

< previous page page_142 next page >

Page 142

(P3)Every element

belongs to at least one (and therefore by (P2) exactly one) element of

The elements of

are called the

blocks

of the partition.

Examples 7.1.1 Some examples of partitions.

(1) Let

and

Then

is a partition of

containing four blocks.

(2) The set of natural numbers can be partitioned into two blocks: the set of even numbers, and the

set of odd numbers.

(3) The set can be partitioned into three blocks: those numbers divisible by 3, those numbers that

leave remainder 1 when divided by 3, and those numbers that leave remainder 2 when divided by 3.

(4) The set

can be partitioned into infinitely many blocks: consider the set of all lines

of the form

where

is any real number. Each point of lies on exactly one line of the form

A partition is defined in terms of the set

and the set of blocks

. However, there is an alternative way

of presenting this information that is often useful. With each partition

on a set

we can define a

binary relation ~

as follows:

The proof of the following is left as an exercise.

Lemma 7.1.2

The relation

P is reflexive, symmetric, and transitive.

Any relation on a set that is reflexive, symmetric, and transitive is called an

equivalence relation

. Thus

from each partition we can construct an equivalence relation. In fact, the converse is also true.

Lemma 7.1.3

Let

be an equivalence relation on the set X. For each put

and

Then X

is a partition of X

< previous page page_142 next page >

< previous page page_143 next page >

Page 143

Proof For each

we have that

because ~ is reflexive. Thus (P1) and (P3) hold. Suppose that

. Let . Then

and

. By symmetry

and so by transitivity

. It follows

that

[x]

[y]

. Hence (P2) holds.

The set

is called the ~

-equivalence class

containing

Lemma 7.1.2 tells us how to construct equivalence relations from partitions, and Lemma 7.1.3 tells us

how to construct partitions from equivalence relations. The following theorem tells us what happens

when we perform these two constructions one after the other.

Theorem 7.1.4

Let X be a non-empty set.

(i)

Let P be a partition on X. Then the partition associated with the equivalence relation

P is P

(ii)

Let

be an equivalence relation on X

Then the equivalence relation associated with the partition

Proof (i) Let

be a partition on

. By Lemma 7.1.2, we can define the equivalence relation ~

. Let

[x]

be a ~

-equivalence class. Then iff

iff

and

are in the same block of

. Thus each ~

equivalence class is a block of

. Now let be a block of

and let . Then iff

iff

. Thus

[u]

. It follows that each block of

is a ~

-equivalence class and vice versa. We have

shown that

and

are the same.

(ii) Let ~ be an equivalence relation on

. By Lemma 7.1.3, we can define a partition

/~ on

. Let =

be the equivalence relation defined on

by the partition

/~ according to Lemma 7.1.2. We have that

iff iff

. Thus ~ and = are the same relation.

Notation Let

be an equivalence relation on a set

. Then the

-equivalence class containing

is often

denoted

ρ(x)

Theorem 7.1.4 tells us that partitions on

and equivalence relations on

are two ways of looking at the

same thing. In applications, it is the partition itself that is interesting, but checking that we have a

partition is usually done indirectly by checking that a relation is an equivalence relation.

The following example introduces some notation that we shall use throughout this chapter.

Example 7.1.5 Let

={1, 2, 3, 4} and let

={{2}, {1, 3}, {4}}. Then

is a partition on

. The

equivalence relation ~ associated with

can be described by a set of ordered pairs, and these can be

conveniently described

< previous page page_143 next page >

< previous page page_144 next page >

Page 144

by a table. The table has rows and columns labelled by the elements of

. Thus each square can be

located by means of its co-ordinates:

(a, b)

means the square in row

and column

. The square

(a, b)

is marked with if

and marked with × otherwise. Strictly speaking we need only mark the squares

corresponding to pairs which are ~-related, but I shall use both symbols.

In fact, this table contains redundant information because if

then

. It follows that the squares

beneath the leading diagonal need not be marked. Thus we obtain

We call this the

table form

of the equivalence relation.

Exercises 7.1

1. List all equivalence relations on the set

={1, 2, 3, 4} in:

(i) Partition form.

(ii) As sets of ordered pairs.

(iii) In table form.

2. Prove Lemma 7.1.2.

3. Let

and

be two equivalence relations on a set

(i) Show that if then each

-class is a disjoint union of

-classes.

(ii) Show that

is an equivalence relation. Describe the equivalence classes of

in terms of the

equivalence classes and the

-equivalence classes.

7.2 The indistinguishability relation

In Section 3.1, we described one way of removing unnecessary states from an automaton: the

construction of the accessible part of A, denoted A

, from A. In this section, we shall describe a

different way of reducing the number

< previous page page_144 next page >

< previous page page_145 next page >

Page 145

of states in an automaton without changing the language it recognises. On a point of notation: if

the set of terminal states of a finite automaton, then

T′

is the set of non-terminal states. Let A=

(S, A,

, δ, T)

be an automaton. Two states are said to be distinguishable if there exists such

that

In other words, for some string

the states

and

are not both terminal or both non-terminal. The

states

and

are said to be

indistinguishable

if they are not distinguishable. This means that for each

we have that

Define the relation on the set of states

We call the

indistinguishability relation

. We shall often write rather than when the machine A

is clear. The relation will be our main tool in constructing the minimal automaton of a recognisable

language. The following result is left as an exercise.

Lemma 7.2.1

Let

be an automaton

Then the relation is an equivalence relation on the set of

states of

The next lemma will be useful in the proof of Theorem 7.2.3.

Lemma 7.2.2

If , then s is terminal if and only if t is terminal

Proof Suppose that

is terminal and . Then

terminal means that . But then

and

so . The converse is proved similarly.

Let be a state in an automaton A. Then the class containing

will be denoted by

[s]

or sometimes by

[s]

A. The set of classes will be denoted by .

It can happen, of course, that each pair of states in an automaton is distinguishable. This is an

important case that we single out for a definition. An automaton A is said to be

reduced

if the relation

is equality.

Theorem 7.2.3 (Reduction of an automaton)

Let

(S, A, s

, δ, T) be a finite automaton

Then

there is an automaton

which is reduced and recognises L

(A).

In addition, if

is accessible then

is accessible

Proof Define the machine as follows:

• The set of states is

< previous page page_145 next page >

< previous page page_146 next page >

Page 146

• The input alphabet is

• The initial state is

]

• The set of terminal states is .

• The transition function is defined by

[s]

for each .

To show that the transition function is well-defined, we need the following result: if

[s]

[s′]

and

then

[s′

. To verify this is true let . Then precisely when . But

and so

Hence precisely when . It follows that . Thus

[s′

a].

We have

therefore proved that is a well-defined automaton. A simple induction argument shows that

[s]

x=[s

for each .

We can now prove that is reduced. Let

[s]

and

[t]

be a pair of indistinguishable states in . By

definition,

[s]

is terminal if and only if

[t]

is terminal for each . Thus

is terminal if and

only if

is terminal. However, by Lemma 7.2.2,

[q]

is terminal in precisely when

is terminal

in A. It follows that

But this simply means that

and

are indistinguishable in A. Hence

[s]

[t],

and so is reduced.

Next we prove that . By definition, precisely when

]

is terminal. This

means that

0·

is terminal and so by Lemma 7.2.2. Thus

Hence .

Finally, we prove that if A is accessible then is accessible. Let

[s]

be a state in . Because A is

accessible there exists such that

0·

. Thus

[s]

0·

]

. It follows that is

accessible.

We denote the automaton by A

and call it A

-reduced

. For each automaton A, the machine

=(A

)

is both accessible and reduced.

Before we describe an algorithm for constructing A

we give an example.

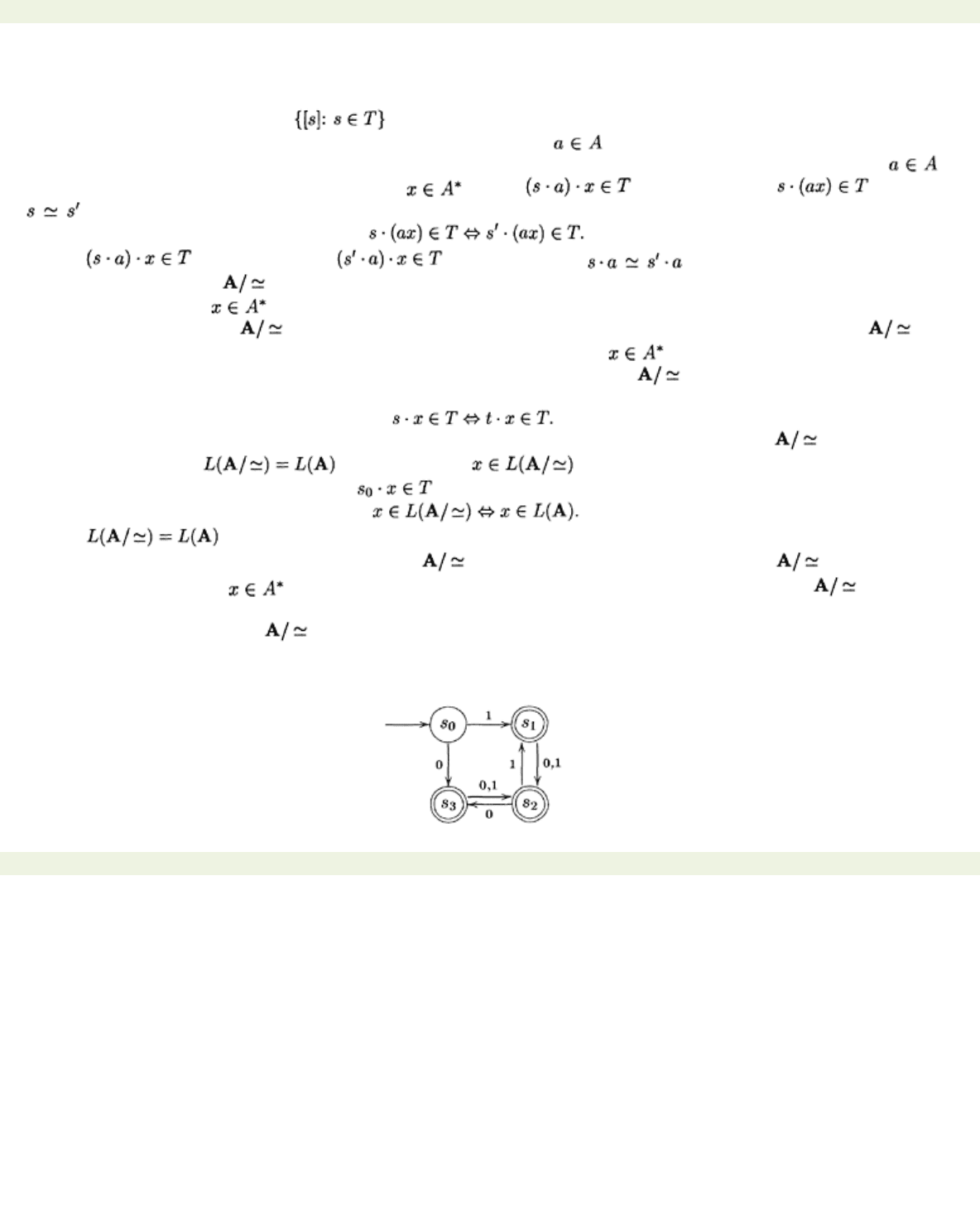
Example 7.2.4 Consider the automaton A below:

< previous page page_146 next page >