Lawson M.V. Finite Automata

Подождите немного. Документ загружается.

< previous page page_157 next page >

Page 157

The number of states in a minimal automaton for a recognisable language

is called the

rank

of the

language

. This can be regarded as a measure of the complexity of

Observe that if A is an automaton, then A

and A

are both reduced and accessible and recognise

(A). So in principle, we could calculate either of these two automata to find the mimimal automaton.

However, it makes sense to compute A

=(A

)

rather than A

. This is because calculating the

reduction of an automaton is more labour intensive than calculating the accessible part. By calculating

first, we will in general reduce the number of states and so decrease the amount of work needed in

the subsequent reduction.

Algorithm 7.4.3 (Minimal automaton) This algorithm computes the minimal automaton for a

recognisable language

from any complete deterministic automaton A recognising

. Calculate A

, the

accessible part of A, using Algorithm 3.1.4. Next calculate the reduction of A

, using Algorithm 7.2.5.

The automaton A

that results is the minimal automaton for

Exercises 7.4

1. Find the rank of each subset of (0+1)2. You should first list all the subsets; construct deterministic

automata that recognise each subset; and finally, convert your automata to minimal automata.

2. Let

≥2. Define

Prove that the rank of

7.5 The method of quotients

In Section 7.4, we showed that if

(A) then the minimal automaton for

is A

. In this section, we

shall construct the minimal automaton of

directly from a regular expression for

. Our method is based

on a new language operation.

Let

be a language over the alphabet

and let . Define the

left quotient of L by u

to be

Similarly, define the

right quotient of L by u

to be

The notation is intended to help you remember the meaning:

< previous page page_157 next page >

< previous page page_158 next page >

Page 158

because we think of

as being cancelled by

−1.

Terminology In this section, I shall deal primarily with left quotients, so when I write ‘quotient,’ I shall

always mean ‘left quotient.’

Examples 7.5.1 Let

be an alphabet, and

a language over

(1)

−1

. Remember that

−1

means

−1

{a}

. By definition iff . Thus

and

. It follows that

−1

(2)

Let . Then and so

. However there is no string

which satisfies this

condition. Consequently .

(3)

This is proved by a similar argument to that in (2) above.

(4)

if and

≠

. Let . Then

. There are no solutions to this equation and

(5)

−1

. By definition iff . This just means that . Hence

−1

The quotients of a regular language, as we shall show, can be used to construct the minimal automaton

of the language. So we shall need to develop ways of computing quotients efficiently. To do this, the

following simple definition will be invaluable. Let

be any language. Define

Thus

δ(L)

simply records the absence or presence of

in the language. The following lemma provides

the tools necessary for computing

for any language given by means of a regular expression. The

proofs are straightforward and left as exercises.1

Lemma 7.5.2

Let A be an alphabet and L,

(i)

for each .

(ii) .

(iii)

δ(ε)

(iv)

δ(LM)

δ(L)

δ(M)

(v)

(

δ(L)

δ(M)

1This just repeats the first part of Lemma 6.2.3.

< previous page page_158 next page >

< previous page page_159 next page >

Page 159

(vi)

δ(L

)

We now show how to compute quotients.

Proposition 7.5.3

Let u, and .

(i)

or ε then u

−1

(LM)

L(u

−1

(ii)

If is any family of languages then .

(iii)

−1

(LM)

−1

L)M

δ(L)(a

−1

(iv)

−1

L)L

(v)

(uv)

−1

Proof (i) Straightforward.

(ii) By definition

iff . But implies for some . Thus

for some . It follows that . The converse is proved similarly.

(iii) Write

δ(L)

0 where

. Then

using (i) and (ii). It is therefore enough to prove the result for the case where

does not contain

. We

have to prove that

. Let . Then

where and and

≠

ε,

by assumption. Thus

al′

for

some

l′

. It follows that

l′m

. Also iff . Thus . Conversely, if

then

l'm

for some and . But then and so .

(iv) By definition iff . Thus

…un

for some non-empty . Now

for

some

. Hence

u(u

…un),

where . Thus . Conversely, if then

u(u

…un)

for some . It follows that and so . Hence .

(v) By definition

iff iff iff iff . Hence

(uv)

−1

It is important to note that in parts (iii) and (iv) above we have derived expressions for quotients by

means of a

single letter only

. We shall deal with the general case in Proposition 7.5.15.

Examples 7.5.4 In the examples below,

{a, b}

< previous page page_159 next page >

< previous page page_160 next page >

Page 160

(1)

−1

A={ε}

. We can write

. Thus

(2)

−1

*. This is straightforward.

(3) Let

be a non-empty string that does not begin with

. Then . This is because

iff . But

does not begin with

. So there is no solution for

(4)

−1

(axA

)

This is

because iff . This can only be true if .

(5) Calculate

−1

abaA

)

. We can regard

abaA

* as a product of two languages in a number or

ways, any one of which can be chosen. We choose to regard it as

* followed by

abaA

*. Thus by

Proposition 7.5.3(iii), we have that

We have already shown that

−1

* and that

−1

(abaA

)

baA

*. Thus

We now prove two important results.

Proposition 7.5.5

(i)

The left (respectively right) quotient of a recognisable language is recognisable.

(ii)

A recognisable language has only a finite number of distinct left (respectively right) quotients.

Proof (i) Let

be a recognisable language. Then

(A) where A=

(S, A, i, δ, T)

is an automaton. We

prove first that every left quotient of

is recognisable. Let and put

i′

. Put A

(S, A, i′, δ,

. We claim that

−1

L. Let

. Then . Thus and so by

Proposition 1.5.4. Hence

giving . We have therefore proved that . To

prove the reverse inclusion let . Then and so . By Proposition 1.5.4, this

means that and so . Hence

as required.

To prove that the right quotient of a recognisable language is recognisable we use the above result and

Proposition 3.3.1. Observe that iff iff iff . It follows

that

< previous page page_160 next page >

< previous page page_161 next page >

Page 161

Thus

The fact that

is recognisable implies that rev

(L)

is recognisable by Proposition 3.3.1. By our result

above rev

(u)

−1rev

(L)

is recognisable, and so by Proposition 3.3.1 again, rev(rev

(u)

−1rev

(L)

) is

recognisable. Hence

−1 is recognisable.

(ii) To finish off, we have to prove that there are only finitely many left quotients. The result for right

quotients then follows by the results in (i). Now the set of left quotients of

is just the set of languages

), where A

(S, A, s, δ, T)

and

and there are clearly only a finite number of these.

We can also prove the converse of the above result.

Proposition 7.5.6

Let L be a language with only a finite number of distinct left (respectively right)

quotients. Then L is recognisable.

Proof We need only prove the result for left quotients. We shall construct a finite automaton A

(S, A,

i, δ, T)

such that

(A)=

. Define

•

which is finite by assumption.

•

−1

•

;

those quotients of

which contain

•

δ(u

−1

L, a)

−1

(ua)

−1

using Proposition 7.5.3(v).

By construction, A

is a complete deterministic automaton. To calculate

) we need to determine

*. We claim that

for each

. We leave the proof of this as an exercise.

By definition, iff iff . From the form of

* and the definition of

this

is equivalent to

which means precisely that . Hence

Combining Propositions 7.5.5 and 7.5.6, we now have the following new characterisation of recognisable

languages.

Theorem 7.5.7

A language is recognisable if and only if it has a finite number of distinct left

(respectively right) quotients.

The automaton A

constructed from a recognisable language

in Proposition 7.5.6 is the best we can

hope for.

< previous page page_161 next page >

< previous page page_162 next page >

Page 162

Theorem 7.5.8

Let L be a recognisable language. Then

L is the minimal automaton of L

Proof By Theorem 7.4.2, it is enough to show that A

is reduced and accessible. The proof that A

accessible is almost immediate: let

−1

be an arbitrary state in A

. Then

(L, u)

−1

and

is the

initial state and so A

is accessible. To prove that A

is reduced, suppose that . Then by

definition, for each

we have that

This is equivalent to saying that for each

we have that

In other words, . Hence

−1

We now describe an algorithm that takes as input a regular expression for a language

and produces

as output the minimal automaton A

. This algorithm has one drawback, which we explain after Example

7.5.13.

Algorithm 7.5.9 (Method of Quotients) Given a regular expression for the recognisable language

this algorithm constructs the minimal automaton for

. We denote the regular expression describing

also by

. We shall construct the transition tree of A

, the automaton defined in Proposition 7.5.6,

directly from

. It is then an easy matter to construct A

which is the minimum automaton by Theorem

7.5.8.

(1) The root of the tree is

. For each calculate

−1

using Proposition 7.5.3. Join

−1

an arrow labelled

. Any repetitions should be closed with a ×.

(2) Subsequently, for each non-closed vertex

calculate

−1

for each using Proposition 7.5.3.

Close repetitions using ×.

(3) The algorithm terminates when all leaves are closed. Mark with double circles all labels containing

The tree is now the transition tree of A

, and so A

can be constructed in the usual way.

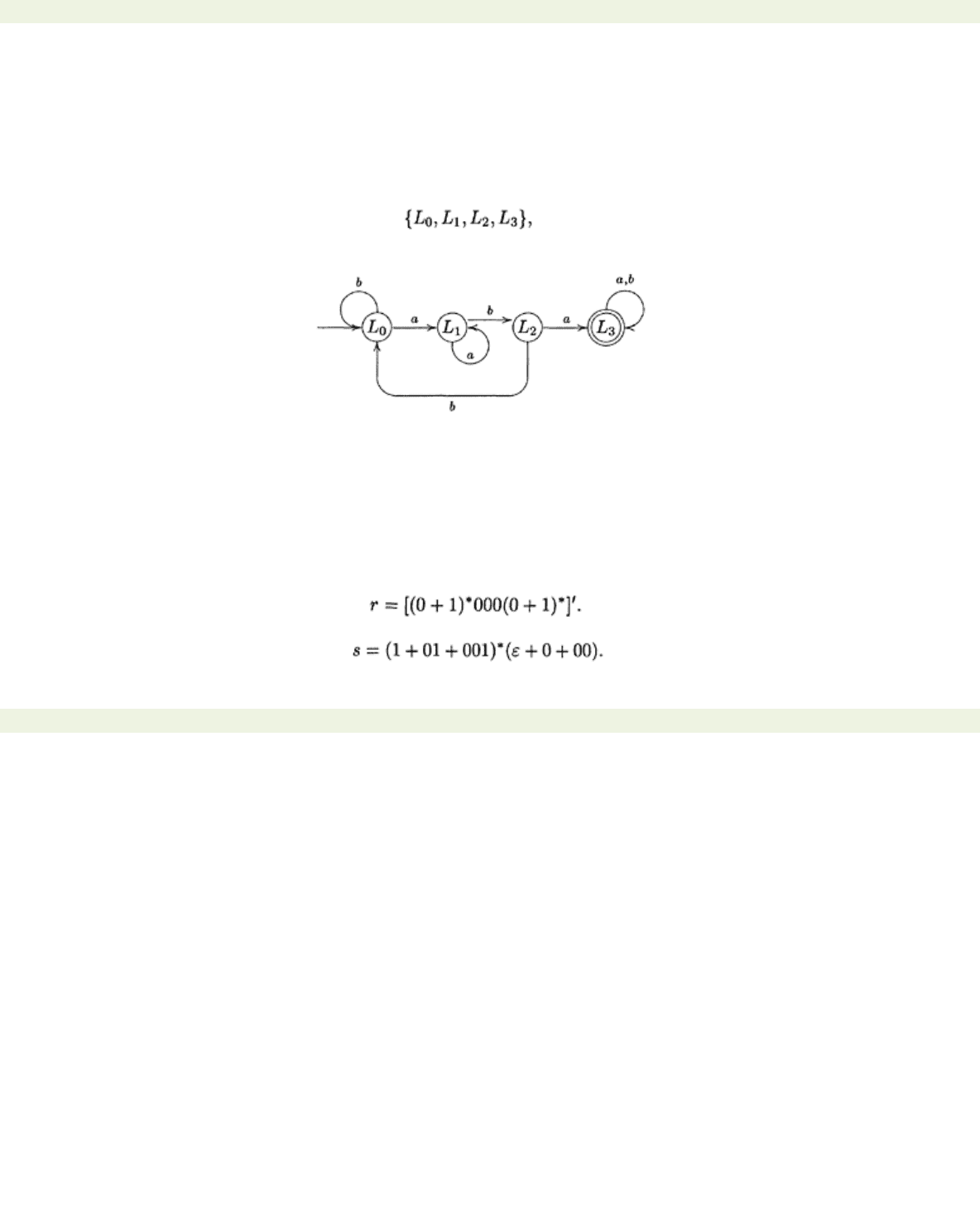
Example 7.5.10 Let

{a, b}

and

aba

(

)*. We find A

using the algorithm above.

(1)

−1

0. By Examples 7.5.1(5).

(2)

−1

baA

1. By Examples 7.5.4(5).

(3)

−1

closed. By Proposition 7.5.3(iii) and Examples 7.5.4(3), and Examples 7.5.4(2).

< previous page page_162 next page >

< previous page page_163 next page >

Page 163

(4)

−1

closed. By Proposition 7.5.3(ii) and Examples 7.5.4(3).

(5)

−1

2. By Proposition 7.5.3(ii) and Examples 7.5.4(3) (adapted).

(6)

−1

3. By Proposition 7.5.3 and Examples 7.5.4(4).

(7)

−1

closed. By Proposition 7.5.4 and Examples 7.5.4(3).

(8)

−1

closed. By Examples 7.5.4(2).

(9)

−1

closed. By Examples 7.5.4(2).

The states of A

are therefore

with

0 as the initial state. The only quotient of

that contains

3 and so this is the terminal state.

The minimal automaton for

is therefore as follows:

The Method of Quotients has an important extra feature. Regular expressions are defined using only +,

·, and *, even though we know that the complement of a regular language is regular. We define a

generalised regular expression

to be a regular expression in the usual sense except that we also allow

complementation, which we denote by ′. By De Morgan’s laws, if we can do union and complementation

we can do intersection. It follows that generalised regular expressions can contain arbitrary Boolean

operations. Generalised regular expressions are often a much more natural way of describing

recognisable languages. Here is an example.

Example 7.5.11 Let

={0, 1}. Consider the language consisting of all strings over

that do not

contain three consecutive 0’s. A generalised regular expression describing this language is

After some thought, we can construct a regular expression describing the same language:

Clearly

is a more natural way of describing this language than

< previous page page_163 next page >

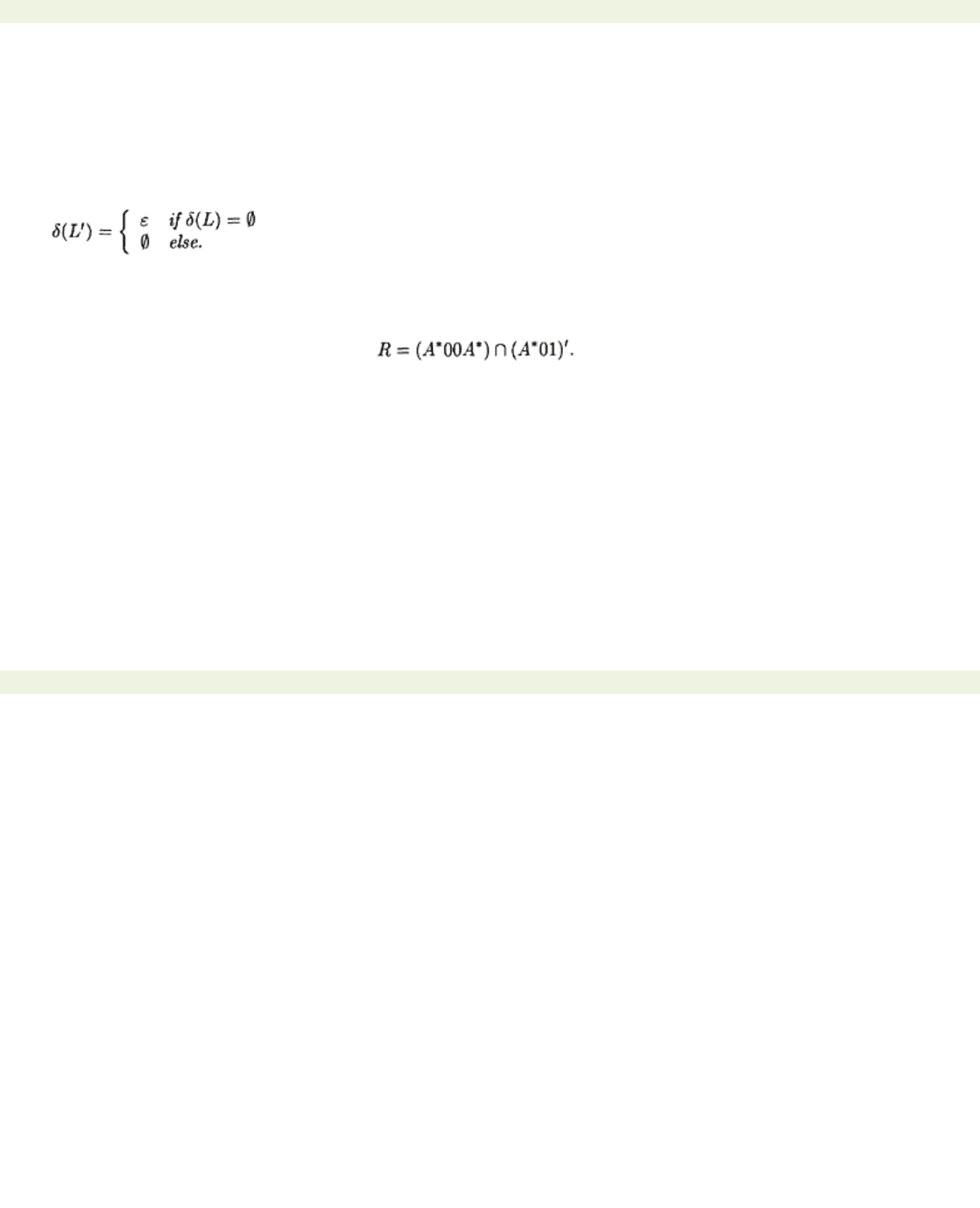
< previous page page_164 next page >

Page 164

The problem with the complementation operation, which is the essential new ingredient distinguishing

generalised regular expressions from regular expressions, is that it is only easy to handle for

deterministic

automata. Our algorithm proving one-half of Kleene’s Theorem using

-automata does not

enable us to handle complementation. A similar problem arises with Algorithm 6.2.2 via ‘linearisation.’

However, the Method of Quotients can easily be extended to handle generalised regular expressions.

The following lemma is all that is needed. The proofs are left as simple exercises.

Lemma 7.5.12

Let A be an alphabet and L a language over A.

(i)

(ii)

−1

(L′)

−1

L)′

Example 7.5.13 We wish to construct an automaton to recognise all those strings over the alphabet

={0, 1}, which consist of two consecutive 0’s but do not end in 01. A generalised regular expression

describing this language is

We shall now apply the Method of Quotients to construct a deterministic automaton recognising this

language. It will aid our calculations to put

*00

* and

*01. We leave to the reader the

verification of the following calculations and the construction of a corresponding automaton A:

(1)

−1

(2) 0−1

*)n(

+1)′=

(3) 1−1

closed.

(4) (0−1

1=(

+1)′=L2.

(5) 1−1

)′. Here we have to be careful because

)′=

Q′

ε′

. Now

ε′

+ and

does

not contain

and so

ε′

. It follows that

)′=

Q′

(6) 0−1

closed.

(7) 1−1

2=(

)′=

(8) 0−1

closed.

(9) 1−1

Q′

(10) 0−1

closed.

< previous page page_164 next page >

< previous page page_165 next page >

Page 165

(11) 1−1

closed.

We conclude this section by discussing the one drawback of the Method of Quotients. For the Method of

Quotients to work, we have to recognise when two quotients are equal as in step (5) in Example 7.5.13

above. However, we saw in Section 5.1 that checking whether two regular expressions are equal is not

always easy. If we do not recognise that two quotients are equal, then the machine we obtain will no

longer be minimal. Here is another example.

Example 7.5.14 Consider the regular expression,

We calculate

−1

(aa)

a(aa)

*. This looks different from

. However,

and so

. It follows that

−1

Two questions are raised by this problem:

Question 1 Could Algorithm 7.5.9 fail to terminate?

Question 2 If it does terminate, what can we say about the automaton described by the transition

tree?

The answer to Question 1 is ‘yes’ but, as long as we do even a small amount of checking, we can

guarantee that the algorithm will always terminate. The answer to Question 2 is that if we fail to

recognise when two quotients are the same, then we shall obtain an accessible deterministic automaton

but not necessarily one that is reduced. It follows that once we have applied the Method of Quotients

we should calculate the indistinguishability relation of the resulting automaton as a check. In what

follows, we justify these two answers.

We say that two regular expressions are

similar

if one can be obtained from the other by using the

following properties of union: idempotence, commutativity, and associativity. It is not hard to check that

similarity is an equivalence relation on the set of regular expressions. Two regular expressions that are

not similar are said to be

dissimilar

. If two regular expressions are similar they are certainly equal, but

the equality of regular expressions does not in general imply their similarity. Proposition 7.5.16 below

tells us that as long as we can check whether two regular expressions are similar or not, then we will

construct a finite number of quotients. To prove this result we shall need to extend Proposition 7.5.3.

< previous page page_165 next page >

< previous page page_166 next page >

Page 166

Proposition 7.5.15

Let L and M be languages over A, and let .

(i) .

(ii)

where δ(x, y) is either or ε.

Proof (i) We prove the result by induction on the length of the string

. We have already proved in

Proposition 7.5.3(iii) that the formula is correct when

has length 1. Assume the result is correct when

the string has length

. We prove that this implies the formula is correct for strings of length

+1. Let

+1. Then

where

has length

. By Proposition 7.5.3(v), we have that

Thus

By Proposition 7.5.3(i), (ii) and (v), this is equal to

which is equal to the required result.

(ii) By Proposition 7.5.3(iv), the result is true when |

|=1. Assume the formula is true for strings

length

. We prove the formula is true for strings of length

+1. Let

where

has length

. Then

which is equal to

using various parts of Proposition 7.5.3 which in turn is of the form,

as required.

In the result above, the notation

δ(x, y)

can take either the value or the value

ε,

but we do not know

which in general.

< previous page page_166 next page >