Лекции по курсу - Технология и автоматизация производства электронной аппаратуры

Подождите немного. Документ загружается.

171

=С

/С

– постоянная времени воздействия, называемая временем изодрома

или временем удвоения; Т

пр

=С

/С

– постоянная времени воздействия скорости

отклонения параметра, называемая временем предварения.

Дискретный аналог ПИД-закона регулирования имеет вид

u(t)=К

ε[nT]+K

Σε[iT]+K

{ε[nT]-ε[(n-1)T]},

(18.11)

где: u(t) – выходная величина регулятора (управляющее воздействие на объект);

ε[nT] – отклонение действительного значения регулируемой величины от за-

данного в моменты времени Т, 2Т, …, nТ, а К

, К

– коэффициенты.

В общем случае цифровой автоматический регулятор (ЦАР) состоит, как и

непрерывный, из входных устройств, вычислителя и выходных устройств.

Структура всех этих устройств и структурная схема цифрового автоматическо-

го регулятора в целом зависит от ЗР и способа его реализации, от формы вход-

ного и выходного сигналов и от др. факторов.

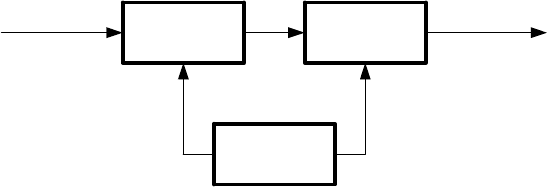
Вычислительное устройство ЦАР

включает (см. рис. 18.8) блок настройки (БН), блок цифровых операторов

(БЦО) и блок управления (БУ) БН предназначен для хранения коэффициентов

настройки К

, К

, а в некоторых случаях осуществляет и умножение откло-

нения на эти коэффициенты, БУ обеспечивает последовательность работы всех

блоков ЦАР в соответствии с принятым алгоритмом, это совокупность логиче-

ских устройств, а БЦО вычисляет основные операции по вычислению состав-

ляющих закона регулирования.

e*[nT] u*[nT]

БН

БУ

БЦО

Рис. 18.8.

172

ЛЕКЦИЯ 19

ПРИНЦИПЫ И СИСТЕМЫ ФУНКЦИОНИРОВАНИЯ

ИНТЕГРИРОВАННЫХ АВТОМАТИЗИРОВАННЫХ СИСТЕМ

УПРАВЛЕНИЯ

Наиболее ранней формой управления технологическими процессами (ТП)

было управление с помощью ручных средств. Для измерения управляемых пе-

ременных человек пользовался своими органами. Первой функцией управле-

ния, подвергшейся автоматизации, было измерение.

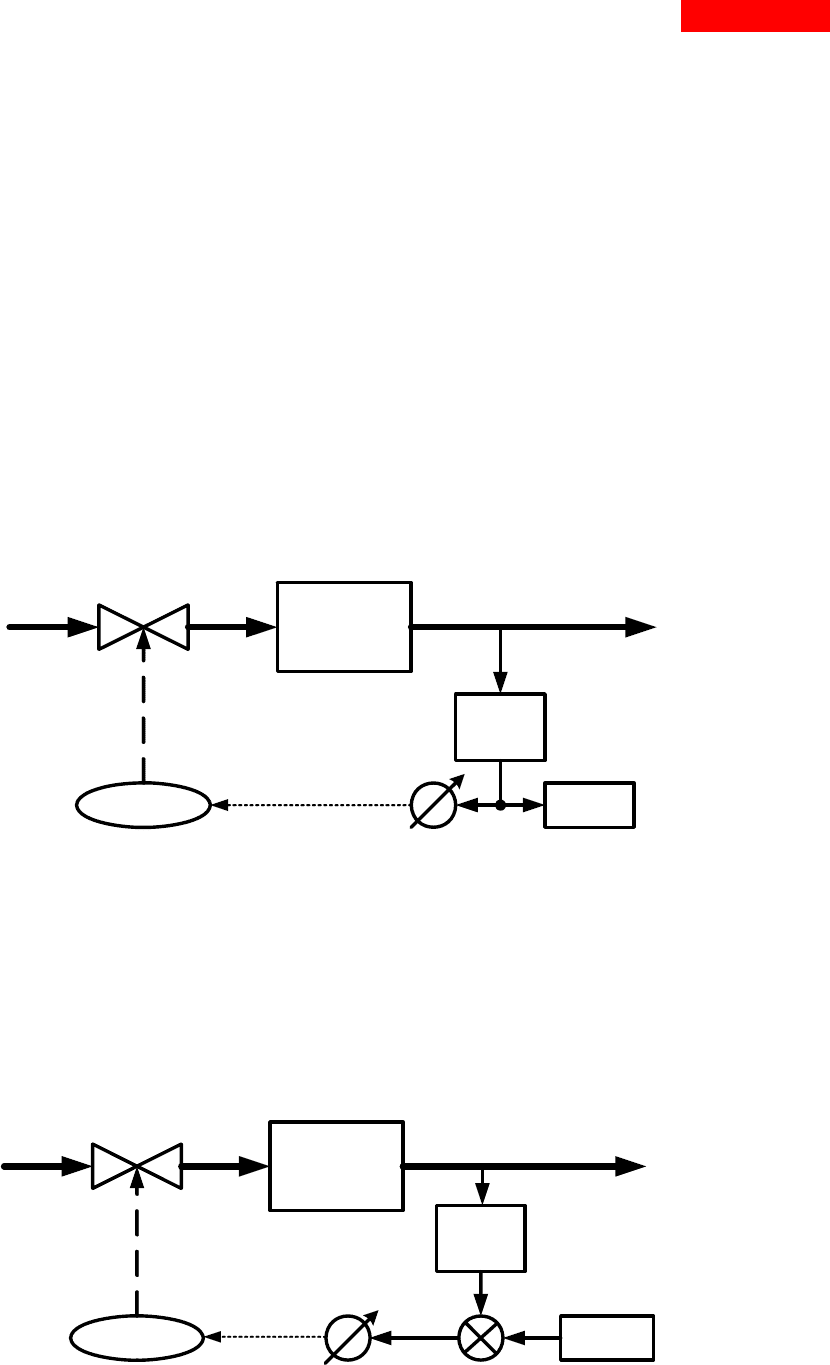
Измерительный прибор с индикатором заменяет органы чувств человека,

обеспечивает быстрые и достаточно точные измерения. Тогда система управле-

ния с автоматическим измерением

и визуальным контролем принимает вид

ТП

датчик

оператор

X’X’’

U=f(|X’’-X’|)

регистратор

индикатор

Рис. 19.1.

Небольшие технические усовершенствования позволили перейти от автома-

тической индикации к автоматическому контролю, а система управления (СУ)

приобрела вид

ТП

датчик

оператор задатчик

X’

e=|X’-X*|

u=f(e)

индикатор

Рис. 19.2.

173

В этом случае оператор получает информацию об отклонении технологиче-

ских параметров от заданных значений.

Система автоматического контроля, кроме измерителя и индикатора, содер-

жит устройство сравнения и задатчик информации – устройство, которое пом-

нит требуемое значение технологического параметра.

По мере усложнения технологических процессов, повышения скорости их

протекания, увеличения числа контролируемых переменных и ужесточения

требований к точности поддержания ТП на заданном уровне появилась необхо-

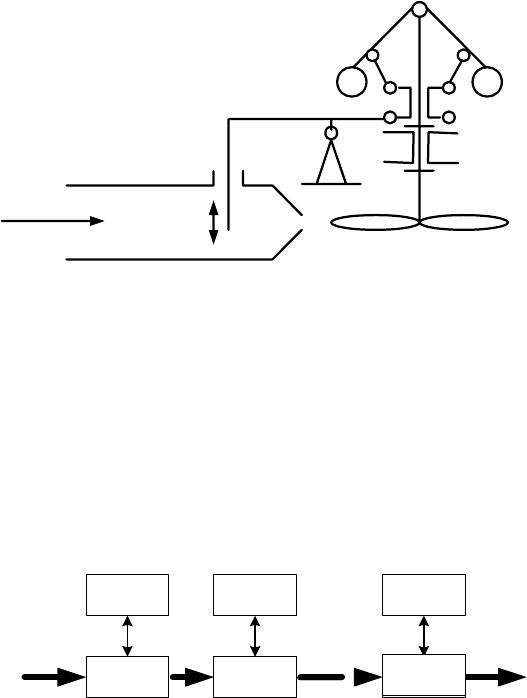
димость в создании автоматических регуляторов. Одним из первых, используе-

мых в промышленности, был регулятор числа оборотов паровой машины Уатта.

пар

задвижка

Рис. 19.3.

Т. о., системы автоматической индикации, контроля и регулирования разли-

чаются степенью автоматизации функций управления.

Наиболее простой структурной организацией таких систем являются одно-

уровневые децентрализованные системы контроля и управления

ПУ

ТП

ПУ

ТП

Рис. 19.4.

Это локальные системы регулирования (управления). Как правило, целесо-

образным оказывается осуществлять контроль и управление отдельными пара-

метрами с централизованного пункта.

174

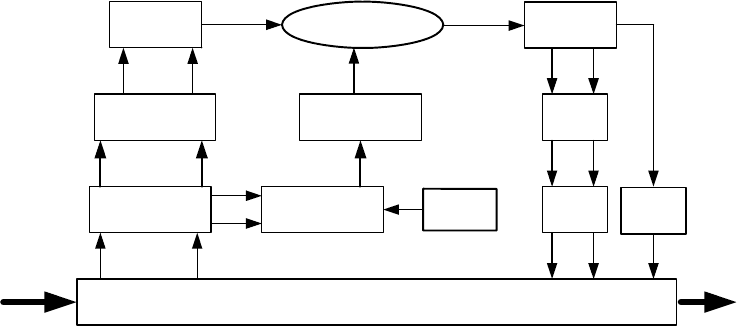
Тенденция централизации управления ТП привела к созданию систем цен-

трализованного контроля или к информационным системам. Вариант структур-

ной схемы системы централизованного контроля приведен на рис. 19.5.

индикаторы индикатор

ИМ

...

оператор

...

ЛР

...

Рег. пр.

Пр. У.

ИМ

коммутатор

ТП

ПУ

датчики

Рис. 19.5.

Системы централизованного контроля выполняют следующие функции: не-

прерывно (периодически) измеряют значения параметров ТП и проверяют их

соответствие заданным значениям, а в случае превышения установленной вели-

чины подают предупредительные сигналы оператору; осуществляют измерение

параметров по инициативе оператора; регистрируют значения параметров про-

цесса; сигнализируют об (пред-) аварийных ситуациях; позволяют оператору

дистанционно изменять уставки

локальных регуляторов или непосредственно

воздействовать на исполнительные механизмы (ИМ); обеспечивают оператив-

ную связь между центральным пунктом управления и технологическими уста-

новками.

Но сложные технологические системы строятся по иерархическому принци-

пу, а для их управления используются иерархические автоматизированные (или

автоматические) системы управления (ИАСУ). Они служат основой создания

автоматических систем управления (АСУ)

гибкого производства и строятся по

принципу многоуровневого управления и обладают определенной структурой в

функциональном, организационном, экономическом и временном аспектах.

На нижнем уровне автоматизированного производства находятся локальные

системы управления (ЛСУ), управляющие работой модулей, на верхнем – сис-

темы управления цехом или производством в целом.

175

Существенные свойства ИАСУ состоят:

1) в последовательном вертикальном расположении подсистем – декомпо-

зиция функций управления;

2) приоритет действий установлен в порядке убывания уровней, т. е. под-

системы более высокого уровня по отношению к подсистемам нижнего уровня

(право вмешательства);

3) в зависимости действий подсистем верхнего уровня от фактического ис-

полнения своих функций подсистем нижнего

уровня.

ИАСУ может иметь разные уровни абстракции:

1) как «черный ящик», выполняющий определенный алгоритм управления

над входными переменными(функциональные задачи);

2) как система с определенной структурой для обработки информации с

целью установления взаимного соответствия между объектами и типами струк-

тур их систем управления;

3) как совокупность технических средств, взаимодействующих одно с дру

гим и реализующих заданную структуру системы.

Описание ИАСУ можно выполнить на уровне математических принципов,

функциональных структур и технических средств.

Для любой АСУ требуется минимум три разных уровня описания:

1) как целостного образования;

2) с точки зрения внутреннего строения;

3) как подсистемы более сложной системы.

Однако, каждый из названных уровней может быть разделен

на элементы

более низкого уровня.

С точки зрения организационной структуры ИАСУ удобно рассматривать

состоящей из нескольких взаимодействующих между собой подсистем, каждая

из которых содержит активный элемент, способный принимать решения.

Активные элементы тоже расположены иерархически, причем активный

элемент верхнего уровня является координирующим по отношению к элемен-

там (как минимум двум) более

низкого уровня, а решение элемента верхнего

176

уровня определяет действия элементов нижнего уровня в соответствии с целью

определенной для всех подчиненных ему элементов.

Активный элемент более высокого уровня оперирует с более инерционными

процессами поведения системы, поэтому времени на принятие решений ему

выделяется больше, чем подчиненным элементам. Активным элементам ниж-

него уровня не должно предписываться жесткое решение, должна быть

предос-

тавлена некоторая свобода в выборе собственных решений, которые могут не

совпадать с решениями верхних активных элементов.

Но такая конфликтная ситуация не должна влиять на достижение глобаль-

ной цели АСУ и возможно лишь в пределах достаточно малых углов отклоне-

ния вектора цели подсистемы от вектора глобальной цели.

Для рассмотрения принципа

функционирования ИАСУ удобно остановиться

на двухуровневой СУ (используя логику предикатов). При этом систему S мож-

но представить через операцию отношения над декартовым произведением

двух множеств

S⊆x×y,

(19.1)

где x×y соответственно множества входов и выходов, x∈X, y∈Y.

Если S – функция, то S:X→Y функциональная система (здесь символ → –

тождественное преобразование).

Каждую систему можно представить конечным числом подсистем С

S=∪С

, по всем i∈I,

(19.2)

где i – элемент индексного множества I.

Т. о., для каждой подсистемы С

основной функцией становится поиск и

принятие решений на своем уровне с учетом координирующих воздействий

вышестоящего уровня.

Теперь систему S можно назвать решающей, если заданы семейства задач

D(x), x∈X с множеством решений R и отображение T:R→Y.

Для любых элементов x∈X и y∈Y пара (x, y)

принадлежит системе S в том и

только в том случае, если существует элемент r∈R, такой, что он является ре-

шением задач D(x) и T(r)=Y. Здесь T – тождественное преобразование R=Y (т. е.

177

выход системы Y рассматривается как решение задачи D(x), конкретизирован-

ной заданием x).

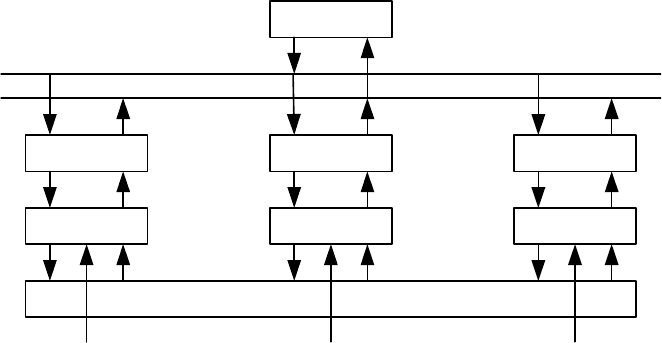
Информационные связи в ИАСУ представимы в виде

...

ТП

Рис. 19.6.

Подсистемы нижнего уровня называемые локальными СУ – это автоматиче-

ские регуляторы, следящие и автоматизированные приводы.

Декомпозицию подсистем 0-го уровня выполняют при определении опти-

мальных вариантов аппаратной и программной реализации АСУ. Обозначив

через j - индекс иерархического уровня, а через I - номер подсистемы на данном

уровне, подсистема C

с j=1 является локальной (ЛСУ). Тогда можно обозна-

чить множество задач через D

решаемых C

, через X

– множество её входов

сигналов от подсистемы уровня (j-1), через Y

– множество выходных (управ-

ляющих) сигналов этой подсистемы, передаваемых на уровень (j-1), через Z

–

множество выходных (информационных) сигналов выдаваемых на (j+1)-й уро-

вень, через U

– множество входных (координирующих)сигналов, поступаю-

щих от вышестоящих подсистем, а Ω - множество внешних возмущений, по-

ступающих из окружающей среды.

Для любой подсистемы верхнего уровня множества управляющих Y

i+1

и вы-

ходных X

j+1

сигналов удобно представить в виде декартовых произведений

множеств

j+1

×U

×…×U

(19.3)

178

j+1

×Z

×…×Z

(19.4)

и рассматривать управляющие сигналы y

j+1

∈Y

j+1

, как n-мерные векторы u

=(u

, …, u

), n

∈U

, а выходные сигналы x

j+1

∈

j+1

как n-мерные компоненты на-

бора

=(z

, z

, …, z

), z

∈Z

(19.5)

причем в системе с i-й нижестоящей подсистемой связаны только i-е компонен-

ты u

, x

, которые для неё являются соответственно входными координирую-

щими и выходными информационными сигналами.

Тогда, любую подсистему C

можно представить в виде системы отображе-

ний

×U

→Y

(19.6)

×U

×Y

→Z

(19.7)

Отображение (20.6) характеризует выработку управляющего воздействия с

учетом координирующего влияния подсистемы более высокого уровня. Считая

подсистему C

решающей, можно Y

представить как множество решений для

семейства связанных с ней задач D

, u

), конкретизированных для каждой

пары из X

, U

Отображение (19.7) показывает подготовку информации в подсистеме для

передачи её на более высокий уровень. Представив ТП P как объединение не-

которого числа подпроцессов P

, каждый из которых управляется ЛСУ C

, что

можно записать в виде

P=∪P

по всем i=[1, n]

(19.8)

Каждый подпроцесс P

можно рассматривать как преобразователь, вырабаты-

вающий сигналы x

) на основе управляющих сигналов y

) с учетом

внешних возмущений

, …,

∈

и воздействий M

, которым он под-

вергается со стороны остальных подпроцессов, тогда

×M

→X

(19.9)

179

т. е. каждая управляющая подсистема 1-го уровня C

решает собственную ло-

кальную задачу управления, являющуюся частью глобальной задачи D

, стоя-

щей перед всей ИСУ.

Поэтому задачу D

можно рассматривать как совокупность локальных задач

, реализуемых подсистемами на всех уровнях. Тогда по всем j и i справедли-

во утверждение D

∪D

. Для нормальной работы системы необходимо, чтобы

цели (задачи) её подсистем были согласованы между собой (согласность и со-

вместимость).

Подсистемы 1-го уровня, непосредственно взаимодействующие с ТП, долж-

ны быть координируемыми относительно глобальной задачи: задачи, решаемые

на нижнем уровне должны быть координируемы также относительно задачи,

решаемой на вышестоящем уровне; ни один из

активных элементов в системе

не может решать всю глобальную задачу – она определяется для всей системы в

целом.

Задачи подсистем нижнего уровня координируемы по отношению к задачам

смежного вышестоящего уровня, если справедливо соотношение

(∃u

)(∃y

)[P(y

, D

))∩P(u

, D

j+1

)],

(19.10)

где D

)={D

), …, D

)} – совокупность задач, решаемых всеми подсис-

темами j-го уровня как множество. Для двухуровневой системы (при i=1, y и u)

(∃u

)(∃y

)[P(y

, D

))∩P(u

, D

)].

(19.11)

Результат решения задачи на j-ом уровне, в свою очередь, должен контроли-

роваться на вышестоящем (j+1)-м уровне и использоваться его активным эле-

ментом при решении задачи D

j+1

. Решение задачи D

j+1

состоит в том, что бы

найти координирующее воздействие y

j+1

, при котором нижестоящие подсис-

темы вырабатывают управляющее воздействие y

∈Y

, Y

×Y

× … ×Y

такое,

что достигается цель координации, т.е. удовлетворение условия, выраженного

некоторым предикатом Q

, y

P(u

, D

j+1

)Ù(∃y

)[Q

, y

)].

(19.12)

Учитывая предыдущие выражения, задача подсистем нижнего уровня коор-

динируема, если справедливо выражение

180

(∃u

)(∃y

)[P(y

, D

))∩Q

, y

)],

(19.13)

а для двухуровневой системы (опуская индексы j при D и Q)

(∃u)(∃y)[P(y, D(u))∩Q(u, y)].

(19.14)

Следовательно, для нормальной работы двухуровневой ИАСУ задачи всех

её подсистем должны быть согласованы с решением глобальной задачи

(∀u)( ∀y){[P(y, D(u))∩Q(u, y)]⇒[P(y, D(u))∩P(y, D

)]}.

(19.15)

А это говорит о том, что выбор стратегии активным элементом (координато-

ром) верхнего уровня во многом определяется конкретной задачей, которую

система решает, и ограничениями, накладываемыми принципами совместимо-

сти и координируемости.

Многоступенчатость в управлении порождает конфликтные ситуации. Ос-

новная причина появления конфликтных ситуаций связана с взаимным влияни-

ем подпроцессов и тем, что

каждый из нижестоящих элементов не имеет ин-

формации о решениях, принятых другими активными элементами того же

уровня.

Поэтому задача координатора состоит в том, чтобы оказать влияние на ни-

жестоящие подсистемы в направлении достижения желаемого (в определенном

смысле) результирующего воздействия.

При этом реализуются различные стратегии: прогнозирование взаимодейст-

вия (координирующие сигналы несут

информацию о предлагаемых взаимодей-

ствиях); оценка воздействия (координатор не сообщает точных оценок, а ука-

зывает лишь возможные области их изменений); согласование взаимодействий

(задачи нижестоящего уровня определяются как полностью автономные. Каж-

дый активный элемент подсистем получает право при решении собственной за-

дачи рассматривать связующие входы как свободные и выбирать их по

собст-

венному усмотрению).