Leroy C., Rancoita P.-G. Principles Of Radiation Interaction In Matter And Detection

Подождите немного. Документ загружается.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

390 Principles of Radiation Interaction in Matter and Detection

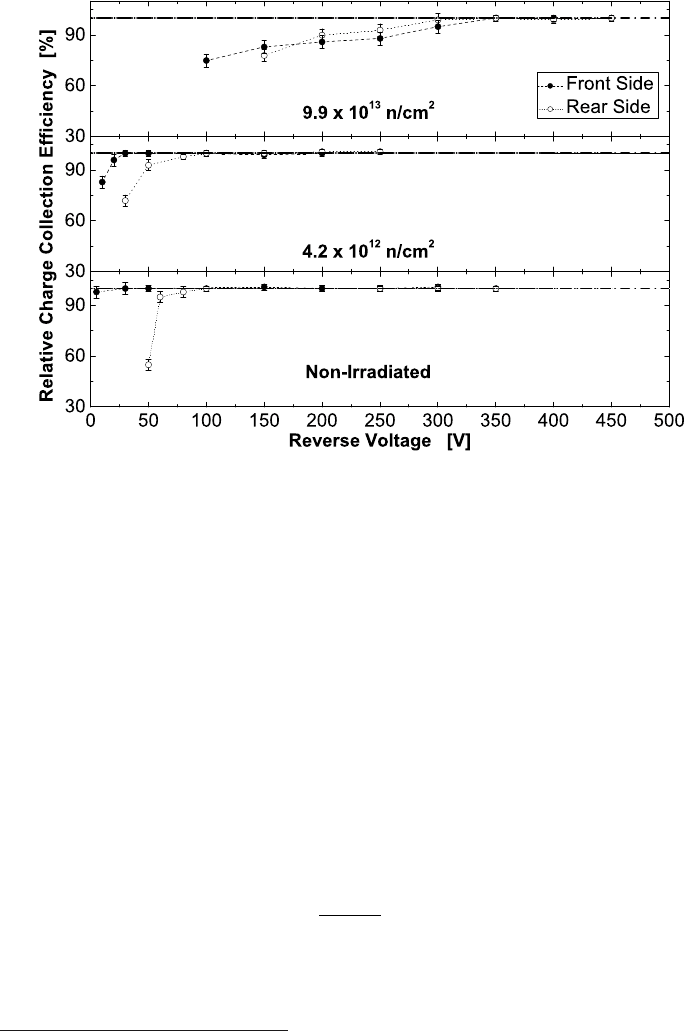
Fig. 4.26 Relative charge-collection eﬃciency (R

eﬀ

, see text at page 393) measured with an

241

Am α-source located at the front (•) and at the rear (◦) of non-irradiated and irradiated silicon

detectors with fast-neutron ﬂuences of 4.2 × 10

n/cm

and 9.9 × 10

n/cm

(from [Leroy and

Rancoita (2007)]; see also [SICAPO Collab. (1994b,c)]). The dashed line and dotted line are to

guide the eye. The dashed and dotted line represents R

eﬀ

= 100%.

irradiation

†

, the forward I −V characteristic is modiﬁed and becomes a function of

the fast-neutron ﬂuence [SICAPO Collab. (1995d)]: a similar behavior was experi-

mentally observed in other silicon detectors and photodiodes {e.g., see, for silicon de-

tectors, [Croitoru, Gambirasio, Rancoita and Seidman (1996); Beattie, Chilingarov

and Sloan (1998, 2000); Granata et al. (2000)] and, for high-resistivity (≈ 5 kΩ cm)

n-type photodiodes, [Korde et al. (1989)]}. In addition [see Eq. (4.138)], at the

ﬂuence of ≈ 10

n/cm

f,irr

depends exponentially on V

(with an ideality factor

of ≈ 2 [SICAPO Collab. (1995d)]) only up to ≈ 0.13 V (i.e., (e V )/(k

T ) ≈ 5). In

practice, for ﬂuences & 1.2 × 10

n/cm

, the experimental data show that I

f,irr

depends linearly on V

[Croitoru, Gambirasio, Rancoita and Seidman (1996)] above

a critical forward voltage V

f,c

which depends, in turn, on the ﬂuence, i.e.,

f,irr

= C

(Φ

) +

(Φ

)

, for V

> V

f,c

(Φ

). (4.140)

f,c

(Φ

) varies from ≈ 1.2 V at the ﬂuence of 1.2 × 10

n/cm

up to ≈ 8 V at

8.9 × 10

n/cm

. At the critical voltage

‡

f,c

, I

f,irr

is 300–350 µA. The absolute

values of C

(Φ

)

are small but not negligible compared with I

f,irr

f,c

). Thus,

†

Experimental data are available up to fast-neutron ﬂuences of ≈ 10

n/cm

‡

Before irradiation, for I

≈ 350 µA we have V

. 0.5 V.

(Φ

) is negative for fast-neutron ﬂuences up to ≈ 1.2 × 10

n/cm

and positive at larger

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Radiation Environments and Damage in Silicon Semiconductors 391

Table 4.6 Values of the parameters m

eﬀ

and b

eﬀ

Eq. (4.143) for Fz-detectors with resistivities ranging from

5 to 7 kΩ cm [SICAPO Collab. (1994b)]. These parameters

have been computed for an α source located at the front

and at the rear side of silicon detectors (from [Leroy and

Rancoita (2007)]).

Front Side Rear Side

eﬀ

(×10

−2

) -5.12 ±0.93 -7.51 ±0.88

eﬀ

1.64 ±0.13 1.94 ±0.12

Eq. (4.140) expresses that the device behaves nearly as an ohmic medium, al-

though a (largely) reduced rectiﬁcation is maintained even at the largest ﬂuence

([Croitoru, Gambirasio, Rancoita and Seidman (1996)], see also [SICAPO Collab.

(1995d); Beattie, Chilingarov and Sloan (1998, 2000); Granata et al. (2000)]). In

Fig. 4.25, the values of the forward resistance (R

) are shown as a function of the

fast-neutron ﬂuence: they approach that of the intrinsic silicon with increasing

ﬂuence.

In these detectors irradiated with fast neutron ﬂuences & 1.2 × 10

n/cm

the reverse I − V characteristics show that the reverse current I

r,irr

monotonously

increases with V

([Croitoru, Gambirasio, Rancoita and Seidman (1996)], see also

[Granata et al. (2000)]), i.e., the current does not approach a constant value as

predicted by Eq. (4.132). At large reverse bias, I

r,irr

becomes linearly dependent on

r,irr

= C

(Φ

) +

(Φ

)

, for V

> V

r,c

(Φ

), (4.141)

where V

r,c

(Φ

) is ≈ 350 V at ﬂuences between 1.2 ×10

and 6 ×10

n/cm

and ≈

90 V at 8.9×10

n/cm

. At the critical voltage V

r,c

, I

r,irr

is ≈ 5.5 µA (≈ 300 µA) at

1.2×10

n/cm

(8.9×10

n/cm

). In Fig. 4.25, the values of the reverse resistance

) are shown as a function of the fast-neutron ﬂuence: similarly to those of

the forward resistance, they approach that of the intrinsic silicon with increasing

ﬂuence. The rectiﬁcation ratio, deﬁned as

r/f

(Φ

) =

(Φ

)

(Φ

)

, (4.142)

is ≈ 1.27×10

at 1.2×10

n/cm

and decreases down to ≈ 14.8 at 8.9×10

n/cm

In silicon rectifying diodes

‡‡

, similarly to low-doped detectors, an increase of the

fast-neutron ﬂuence causes a decrease of the forward I − V characteristic. At large

ﬂuences [Croitoru, Gambirasio, Rancoita and Seidman (1996)].

‡‡

One can see, e.g., [Easley (1962); Frank, Poblenz and Howard (1963)], Section 1 in Chapter II of

Part II of [Vavilov and Ukhin (1977)] and also Sections 6.5 and 6.8.1 of [Holmes-Siedle and Adams

(2002)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

392 Principles of Radiation Interaction in Matter and Detection

ﬂuences, the I − V characteristic for both p − n and p − i − n rectifying diodes is

approximately expressed by Eq. (4.140), where C

(Φ

), R

(Φ

) and V

f,c

(Φ

) depend

on the dopant concentrations. In addition, in p − n diodes V

(Φ

) increases with

increasing base thickness; in p−i−n diodes it increases with increasing the thickness

of the quasi-intrinsic i-layer (Figs. 82–85 at pages 204–207 of [Vavilov and Ukhin

(1977)], see also [Shwartz et al. (1966)]). The experimental data on silicon p−n and

p − i − n irradiated diodes show a qualitative and quantitative agreement with the

predictions based on the Vavilov–Ukhin model (see pages 188–208 of [Vavilov and

Ukhin (1977)]).

4.3.3.2 Large Radiation Damage and p −i −n Structure at Room Tempe-

rature

It has been observed that p − n diodes, with resistivities of several Ω cm, may

gradually change their internal structure with increasing fast-neutron ﬂuence. In

fact, non-irradiated diodes with an ohmic (n

-) contact can acquire a p − i − n

structure after irradiation. This was determined, for instance, by measurements

of the potential distribution with respect to the p-region using the method of a

moving probe. These measurements show that, in a forward-biased device with a

resistivity of ≈ 32 Ω cm, an increased voltage drop occurs in the base-region and in

the ohmic-contact with increasing neutron ﬂuence above ≈ 2 ×10

n/cm

(e.g., see

Fig. 86 at page 208 of [Vavilov and Ukhin (1977)]). The n

− n ohmic-contact

properties are conserved in lower resistivities devices (≈ 2.1 Ω cm) up to ﬂuence of

≈ 2 × 10

n/cm

Similarly to low-resistivity p − n diodes, n-type detectors with an n

-region as

ohmic-contact (e.g., see Sect. 4.3.3.1) gradually change their internal structure. In

fact, with increasing particle ﬂuence, the n-doped region becomes almost intrinsic

(i, i.e., very weakly doped) and the n

-layer behaves like a rectifying region. In addi-

tion, at fast-neutron ﬂuences of ≈ 10

n/cm

, the behavior of the p

−n device has

been found to be compatible with that of a p

−i−n

diode with an ambipolar dif-

fusion length (e.g., see page 389) of ≈ 200 µm [SICAPO Collab. (1995d)]. This phe-

nomenon has been conﬁrmed [SICAPO Collab. (1994b,c)] by employing fast shaped

electronics [i.e., shaped signals of (20–25) ns peaking-time and ≈ 120 ns base-time]

for measuring the charge collection

, when an

241

Am α-source is located at the front

or at the rear of non-irradiated and irradiated silicon detectors

. The total range

of an α-particle from an

241

Am source is about 25 µm in silicon. As a consequence,

the depleted layer width must be ≥ 25 µm in order to obtain the maximum (or full)

charge-collection. Before irradiation (see Fig.4.26), full charge-collection is achieved

at low reverse bias (a few volts), when the source is located at the front of the de-

A treatment of the charge transport and collection in silicon diodes can be found in the chapter on

Solid State Detectors (see also Sects. 6.1.4, 6.1.5 and 6.8.2).

These devices are Fz-silicon detectors (400 µm thick) with resistivities ranging from 5 to 7 kΩ cm

[SICAPO Collab. (1994b)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Radiation Environments and Damage in Silicon Semiconductors 393

tector (i.e., of the p

-region), while the reverse voltage for full depletion (≈ 100 V)

is needed to achieve a full charge-collection when the source is located at the rear

side of the detector (i.e., of the n

-layer for the ohmic-contact). Furthermore, the

reverse voltage for maximum charge-collection increases with increasing ﬂuence

∗∗

(e.g., see Fig. 4.26 for 4.2 × 10

n/cm

and 9.9 × 10

n/cm

). At the ﬂuence of

9.9 × 10

n/cm

(Fig. 4.26), the maximum charge-collection is obtained for an ap-

plied reverse voltage of ≈ 350 V. As expected

∗

, the applied voltage exceeds largely

that needed for full charge-collection before irradiation. In addition, the front and

rear sides of the detector seem to b ehave similarly, i.e., the device operates as a

double-sided junction and not as an asymmetrical (one-sided) junction [SICAPO

Collab. (1994b)]. In these high resistivity silicon detectors, the charge-collection

eﬃciency (e.g., see Sect. 6.8.2), i.e., the ratio R

eﬀ

of the charge collected after irra-

diation with respect to that of before irradiation, was found to have a logarithmic

dependence on ﬂuence. The charge collected is roughly that before irradiation up

to a ﬂuence of ≈ 3.2 × 10

n/cm

[SICAPO Collab. (1994b)]. Above this ﬂuence,

eﬀ

decreases and is given by

eﬀ

∼ m

eﬀ

ln (Φ

) + b

eﬀ

, for Φ

> 3.2 × 10

n/cm

, (4.143)

where Φ

is the fast-neutron ﬂuence, and the coeﬃcients m

eﬀ

and b

eﬀ

, for

Fz-detectors with resistivities ranging from 5 to 7 kΩ cm, are shown in Ta-

ble 4.6 [SICAPO Collab. (1994b)]. R

eﬀ

slightly depends on the location of the

α-source, i.e., at the front or at the rear side of the silicon detector

††

. In Fig. 4.26,

the relative charge-collection eﬃciency (as a function of the applied reverse voltage)

is the fraction (in percentage) of the charge collected with respect to the maximum

charge collected after irradiation whose R

eﬀ

is expressed by means of Eq. (4.143).

After irradiations in the range (1–10)×10

n/cm

, high-resistivity silicon detec-

tors are still capable of measuring the energy-loss deposited by minimum-ionizing-

particles (mips) under both reverse and forward bias [Chilingarov and Sloan (1997);

Beattie, Chilingarov and Sloan (2000)]. To reduce the leakage current, these detec-

tors were operated at moderate low-temperature up to about 249 K.

4.3.3.3 I − V Characteristics Down to Cryogenic Temperature

The carrier concentration of an extrinsic non-irradiated silicon semiconductor re-

mains essentially constant over a wide range of temperature below 300 K. However,

at low temperature the dopant atoms are no longer fully ionized

‡‡

and the electron

(hole) concentration depends on the concentration of acceptors (donors) contained

in n-type (p-type) silicon. In fact, sophisticated puriﬁcation techniques can largely

∗∗

The depletion voltage for full charge-collection decreases with decreasing temperature

(e.g, see [Granata et al. (2000); Santocchia et al. (2004)]).

∗

One can see, e.g., [Rancoita and Seidman (1982); Borgeaud, McEwen, Rancoita and Seidman

(1983); SICAPO Collab. (1994b,c)], see also Section 11.2.4 [Lutz (2001)].

††

Similar results were also obtained with MCZ detectors [SICAPO Collab. (1994c)].

‡‡

This temperature range is also referred to as freeze-out range of temperature.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

394 Principles of Radiation Interaction in Matter and Detection

reduce “unwelcome” impurities, but not eradicate them completely. In addition with

decreasing temperature, while the energy gap (E

) slightly increases, the Fermi level

) approaches the energy level of the main impurity.

For instance, in an n-type extrinsic semiconductor, the electron concentration

) at low (and very low) temperature

∗∗

is given by:

exp

− E

2 k

, for N

¿ n

¿ N

, (4.144)

and

= g

− N

exp

− E

, for n

¿ N

< N

, (4.145)

where N

and N

are the concentrations of donor and acceptors, respectively, with

> N

, E

and E

are the energy level of the principal donor and the energy

of the bottom of the conduction band

∗

, respectively; N

is the eﬀective density-

of-states in the conduction band

†

and g

−1

(= 2) is the ground-state degeneracy

‡

of the simple donor (e.g., Section 1.4.3 of [Sze (1981)] and Section 3.1.1 of [Blake-

more (1987)]). The expressions regarding the hole concentration in a p-type extrin-

sic semiconductor at low temperature can be found, for instance, in Section 3.2.2

of [Blakemore (1987)]. It has to be noted that the intrinsic-carrier concentration

int

) also decreases with decreasing temperature. n

int

is approximately given by

(e.g., Section 3.4.1 of [Wolf (1969)])

int

≈ 3.73 × 10

× T

3/2

exp

−

7.014

× 10

−3

, (4.146)

becomes ∼ 10

−3

at T ∼ 250 K (e.g., see Fig. 3.4.1 at page 179 of [Wolf (1969)],

Fig. 11 at page 19 of [Sze (1981)]) and very small at T ≈ (150–170) K. Other

expressions and comparisons with experimental data can be found in [Barber (1967)]

(see also Sections 1.2.1.3 and 1.2.2.3 of [Guti´errez, Deen and Claeys (2001)]).

Furthermore {e.g. see Equation (322.11) at page 137 of [Blakemore (1987)]} at

very low temperature, the energy of the Fermi level is given by:

∼ E

+ k

T ln

− N

)

for n

¿ N

< N

. (4.147)

By inspection of Eq. (4.147), we see that the Fermi level moves to that of the prin-

ciple donor as T → 0 K. While, as T increases from absolute zero, it (slightly)

∗∗

The reader can see, e.g., Equations (322.7, 322.8) in Section 3.2.2 of [Blakemore (1987)] and,

also, Section 1.4.3 of [Sze (1981)].

∗

− E

is (0.044–0.045) eV for phosphorus at room temperature in silicon (e.g., see Chapter 1

of [Milnes (1973)]).

†

In silicon {e.g., see page 19 of [Sze (1985)] and Equation (220.1) at page 82 of [Blakemore

(1987)]}, N

is 4.829 × 10

(T )/m

]

3/2

−3

, where m

is the electron rest mass

and m

(T ) is the density-of-states eﬀective mass for electrons ≈ 1.18 (1.06) at 300 (4.2) K

(e.g., see [Barber (1967)] and Section 1.2.1.3 of [Guti´errez, Deen and Claeys (2001)]; additional

data can be found in Section 2.7 of [Adachi (2004)]).

‡

For acceptors, the degeneracy factor is 4 {e.g., see Equation (151.1) at page 58 and Equa-

tion (220.1) at page 82 of [Blakemore (1987)] and, also, page 19 of [Sze (1985)]}.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Radiation Environments and Damage in Silicon Semiconductors 395

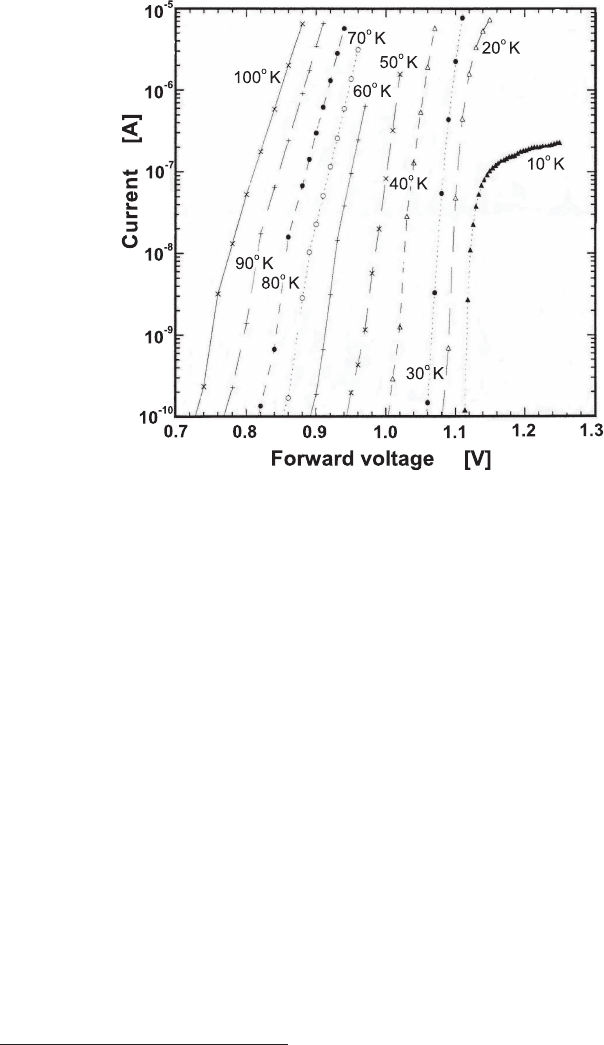
Fig. 4.27 Forward current (in A) as a function of the applied forward voltage (in V) for a non-

irradiated n-type silicon detector and temperatures from 10 up to 100 K (from [Leroy and Rancoita

(2007)]; see also [Croitoru, Rancoita, Rattaggi, Rossi and Seidman (1996, 1997)]).

rises above E

in extrinsic semiconductors with a small compensation [i.e. for

− N

) > N

], before decreasing again at larger temperatures. At 10 K for

an acceptor compensation of about 1 %, E

− E

is ≈ (2–4) meV {Eq. (4.147), see

also Fig. 32.10 at page 137 of [Blakemore (1987)]}.

As mentioned above, the energy gap depends on the temperature: for a weakly

doped Fz-material with N

= 5 × 10

−3

and N

= 10

−3

[Bludau and

Onton (1974)], it is about 1.12 eV at 300 K and about 1.17 eV at (50–10) K (see

also Section 1.2.1.2 of [Guti´errez, Deen and Claeys (2001)] and, for instance, direct

measurements reported in [MacFarlane, McLean, Quarrington and Roberts (1958);

Shklee and Nahory (1970); Bludau and Onton (1974)]).

In Fz n-type detectors

with resistivity of ≈ (4–7) kΩ cm (i.e., a dopant concen-

tration of ≈ 1.1×10

–6.2×10

−3

), the acceptor concentration is typically lower

than 10

−3

. In these n-type extrinsic semiconductors, the freeze-out of dopants

cannot be neglected below ≈ (38–35) K {e.g., [Croitoru, Rancoita, Rattaggi, Rossi

and Seidman (1996)], see also Eqs. (4.144, 4.145)}; at (14–13) K the electron concen-

tration is lower than ≈ 10

−3

and, as a consequence, the medium is practically

an insulator.

These detectors are manufactured by STMicroelectronics.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

396 Principles of Radiation Interaction in Matter and Detection

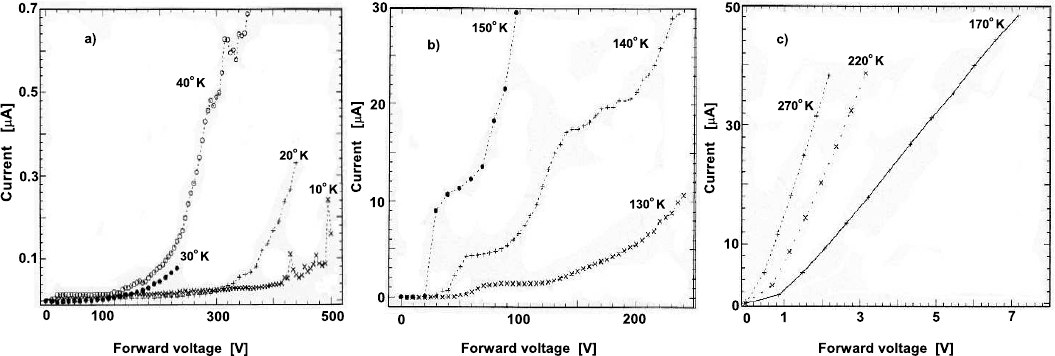
Fig. 4.28 Forward current (in µA) as a function of the applied forward voltage (in V) for an n-type silicon detector irradiated with 5.9 ×10

n/cm

(see also [Croitoru, Rancoita, Rattaggi, Rossi and Seidman (1996, 1997)]): (a) for (10–40) K, (b) for (130–150) K, (c) for (170–270) K {(a) and (b)

from [Leroy and Rancoita (2007)]; (c) from [Rancoita (2008)]}.

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Radiation Environments and Damage in Silicon Semiconductors 397

These devices have a (reverse) leakage current of ≈ 10 nA at room temperature

and lower than ≈ 0.1 nA at ≈ 100 K. In addition, at room temperature, while full

depletion is achieved at a reverse voltage of about 80 V, the device capacitance de-

creases (see Sect. 6.1.3) as 1/

√

until full depletion is achieved; for temperatures

lower than the critical temperature (T

) of about 20 K (see also Sect. 4.3.4), the

capacitance

becomes independent of V

, i.e., the device behaves like an insulator,

where the junction eﬀect is less relevant [Croitoru, Rancoita, Rattaggi, Rossi and

Seidman (1997)]. These phenomena are consistent with the large decrease and the

freeze-out of free carriers at low and very low temperatures. With decreasing tem-

perature (Fig. 4.27), the forward I −V characteristics exhibit an increasingly sharp

dependence on the forward voltage V

, i.e., a lower forward resistance. In addition

[Croitoru, Rancoita, Rattaggi, Rossi and Seidman (1996, 1997)], at 10 K the switch-

ing voltage V

f,s

becomes ≈ 1.12 V, but for V

slightly above V

f,s

(at ≈ 1.14 V) the

forward current increases less sharply (Fig. 4.27).

As already mentioned, when the temperature is within the freeze-out range,

the silicon may be thought of as an insulator. When this occurs, we must consider

the phenomena of single-carrier space-charge-limited current (e.g., see [Shockley

and Prim (1953); Gregory and Jordan (1964)]) and double-injection conduction,

i.e., the Lampert–Ashley–Wagener model (e.g., see [Lampert and Rose (1961); Lam-

pert (1962); Ashley and Milnes (1964); Wagener and Milnes (1964)]), other than

the ohmic conduction. In these mechanisms, the presence of traps can substantially

prevent the conduction upon their ﬁlling. The abrupt increase of the forward current

at the junction voltage

∗∗

(≈ 1.1 V) was already observed in p

−n−n

junctions at

4.2 K [Brown and Jordan (1966)] and explained by extending the Lampert–Ashley–

Wagener model to account for the junction eﬀects [investigated by Jonscher (1961)].

After irradiation, additional traps are created inside the device and, since the

conduction mechanism depends on the concentrations and the energy levels of traps

(e.g., [Ashley and Milnes (1964); Brown and Jordan (1966)]), the I − V forward

characteristics are largely aﬀected at very low temperatures [Fig. 4.28]. At 10 K

[Croitoru, Rancoita, Rattaggi, Rossi and Seidman (1996)], for a neutron ﬂuence of

1.2×10

n/cm

, V

f,s

is about that before irradiation, but becomes > 400 V for 5.9×

n/cm

[Fig. 4.28(a)]. In the framework of double-injection models (e.g., [Ashley

and Milnes (1964); Brown and Jordan (1966)]), the switching voltage depends on the

concentrations of traps to be ﬁlled [Croitoru, Rancoita, Rattaggi, Rossi and Seidman

(1996)] and, as a consequence, can become large at high neutron ﬂuence. In addition,

the critical temperature

††

increases with the neutron ﬂuence [Croitoru, Rancoita,

Rattaggi, Rossi and Seidman (1997)]: for 5.9 × 10

n/cm

is ≈ 150 K, i.e., is

To determine T

, the capacitance measurements were performed with a test frequency of 10 kHz.

f,s

is the average forward voltage for which the forward current increases abruptly from less

than 10

−10

A up to more than 10

−8

∗∗

The junction voltage is described by the Sah–Noyce–Shockley theory [Sah, Noyce and Shockley

(1957)].

††

is ≈ 40 K for 1.2 × 10

n/cm

[Croitoru, Rancoita, Rattaggi, Rossi and Seidman (1997)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

398 Principles of Radiation Interaction in Matter and Detection

larger by about an order of magnitude compared to that before irradiation.

Above the critical temperature, the I −V characteristics exhibit an ohmic beha-

vior which can be expressed by Eq. (4.140), where C

(Φ

) and R

(Φ

) also depend on

the temperature [see for instance Fig. 4.28(c)]. The forward resistance decreases with

increasing temperature: for 5.9×10

n/cm

, R

is ≈ 1.3×10

, 6.6×10

, 5.1×10

Ω

at 170, 220, 270 K, resp ectively [see Fig. 4.28(c)]. At 220 K, for a ﬂuence of

1.2×10

n/cm

the forward resistance is ≈ 2.0×10

Ω [Leroy and Rancoita (2007)].

4.3.4 Complex Junction Impedance and Cryogenic Temperatures

The I − V reverse characteristics of the p

− n diode, considered in Sects. 4.3.2

and 4.3.3, were derived and also measured under the condition that diode voltages

change so slowly that the excess carrier distributions in the two regions of the junc-

tion remain in a steady state. When a small sinusoidal voltage is superimposed to the

dc bias, the current-voltage behavior cannot be expressed by static characteristics,

because the diode shows a capacitive behavior. Thus, at room temperature, the

diode impedance will be described by accounting for both the ohmic and capacitive

parts of the depleted region (e.g., Section 3.5.2 of [Sze (1985)], Section 9.1 of [Tyagi

(1991)] and Section 4.4 of [Shur (1996)]) and, as a consequence, will depend on the

frequency (f ) of the ac signal. However, the so-called diﬀusion capacitance

‡‡

can be

neglected, when a reverse voltage is applied. In addition, since at low temperature

the carriers start to freeze-out (see Sect. 4.3.3.3), the capacitance of the ﬁeld-free

region has been taken into account together with its resistance

∗

in the compre-

hensive model for the Small-signal ac Impedance of a one-sided p

− n Junction

Diode (SIJD) operated under reverse bias [Li (1994a); Croitoru, David, Rancoita,

Rattaggi and Seidman (1997a, 1998b)].

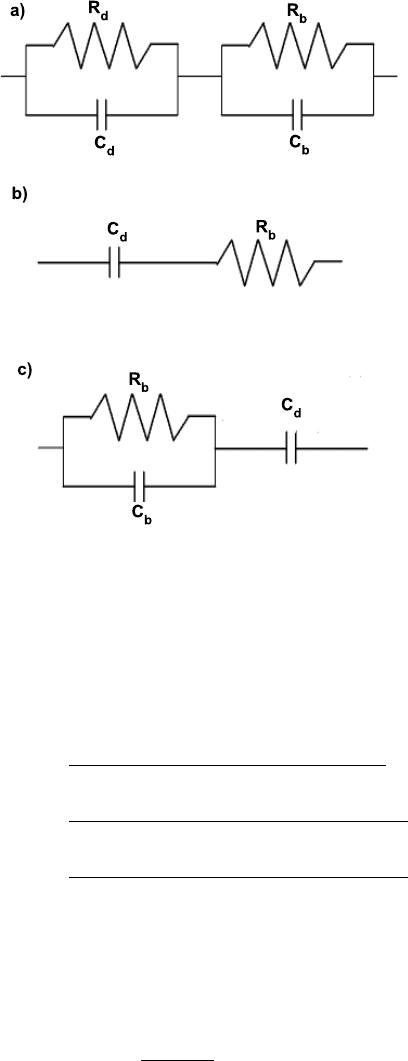
The admittance of the equivalent circuit for the SIJD model [Fig. 4.29(a)] is:

Y (ω) =

(ω)

−1

(ω) Y

(ω)

(ω) + Y

(ω)

, (4.148)

where ω = 2πf,

(ω) =

+ jωC

(4.149)

and

(ω) =

+ jωC

(4.150)

are the admittances of the depleted and ﬁeld-free (i.e., the electrical neutral bulk)

regions, respectively; C

) and C

) are the capacitances (resistances) of

‡‡

The diﬀusion capacitance is related to the minority carriers injected into the neutral region

(e.g., Section 9.1 of [Tyagi (1991)] and Section 4.4 of [Shur (1996)]).

∗

One can see, e.g., [Viswanathan, Divakaruni and Kizziar (1991); Divakaruni, Prabhakar and

Viswanathan (1994)].

January 9, 2009 10:21 World Scientiﬁc Book - 9.75in x 6.5in ws-bo ok975x65˙n˙2nd˙Ed

Radiation Environments and Damage in Silicon Semiconductors 399

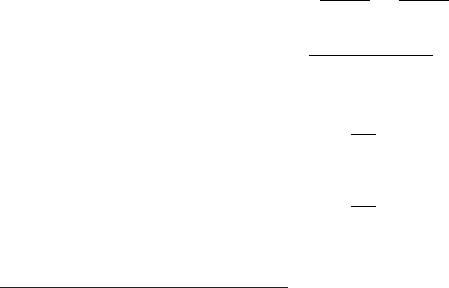
Fig. 4.29 Equivalent circuit for a non-irradiated one-sided junction operated under reverse bias

(from [Leroy and Rancoita (2007)]). C

) and C

) are the capacitances (resistances) of the

depleted and ﬁeld-free regions, respectively: (a) general equivalent circuit, (b) at room temperature

for R

À 1/(ωC

) and R

¿ 1/(ωC

), (c) at low temperature for R

À 1/(ωC

) with ω = 2πf ,

where f is the test frequency.

the depleted and ﬁeld-free regions, respectively. Introducing Eqs. (4.149, 4.150) in

Eq. (4.148), we obtain

Y (ω) =

(1 + jωC

)(1 + jωC

)

(1 + jωC

+ (1 + jωC

1 − ω

+ jω(C

+ C

)

+ R

) + jωR

+ C

)

1 − ω

+ jω(C

+ C

)

+ R

)

+ ω

+ C

)

×[(R

+ R

) − jωR

+ C

)]. (4.151)

Finally, using Eq. (4.151), the admittance of the equivalent circuit for the SIJD

model [Fig. 4.29(a)] becomes:

Y (ω) = G(ω) + j B(ω) (4.152)

r,eﬀ

(ω)

+ j ωC

r,eﬀ

(ω)